北师大版初中数学八年级上册第15讲 正比例函数(基础)(知识讲解+巩固练习)
文档属性
| 名称 | 北师大版初中数学八年级上册第15讲 正比例函数(基础)(知识讲解+巩固练习) |

|
|
| 格式 | zip | ||
| 文件大小 | 155.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-18 23:23:20 | ||
图片预览



文档简介
正比例函数(基础)
【学习目标】
1. 理解正比例函数的概念,能正确画出正比例函数的图象;
2. 能依据图象说出正比例函数的主要性质,解决简单的实际问题.
【要点梳理】
要点一、正比例函数的定义
1、正比例函数的定义
一般的,形如 (为常数,且≠0)的函数,叫做正比例函数.其中叫做比例系数.
2、正比例函数的等价形式
(1)、是的正比例函数;
(2)、(为常数且≠0);
(3)、若与成正比例;
(4)、(为常数且≠0).
要点二、正比例函数的图象与性质
正比例函数(是常数,≠0)的图象是一条经过原点的直线,我们称它为直线.当>0时,直线经过第一、三象限,从左向右上升,即随着的增大也增大;当<0时,直线经过第二、四象限,从左向右下降,即随着的增大反而减小.
要点三、待定系数法求正比例函数的解析式
由于正比例函数(为常数,≠0 )中只有一个待定系数,故只要有一对,的值或一个非原点的点,就可以求得值.
【典型例题】
类型一、正比例函数的定义
1、已知,当为何值时,是的正比例函数?
【思路点拨】正比例函数的一般式为,要特别注意定义满足,的指数为1.
【答案与解析】
解:由题意得, 解得 =2
∴当=2时,是的一次函数.
【总结升华】理解正比例函数的概念应抓住解析式中的两个主要特征:(1)不等于零;(2)的指数是1.
举一反三:
【变式】如果函数是正比例函数,那么的值是________.
【答案】
解:由定义得 解得 ∴ =2.
类型二、正比函数的图象和性质
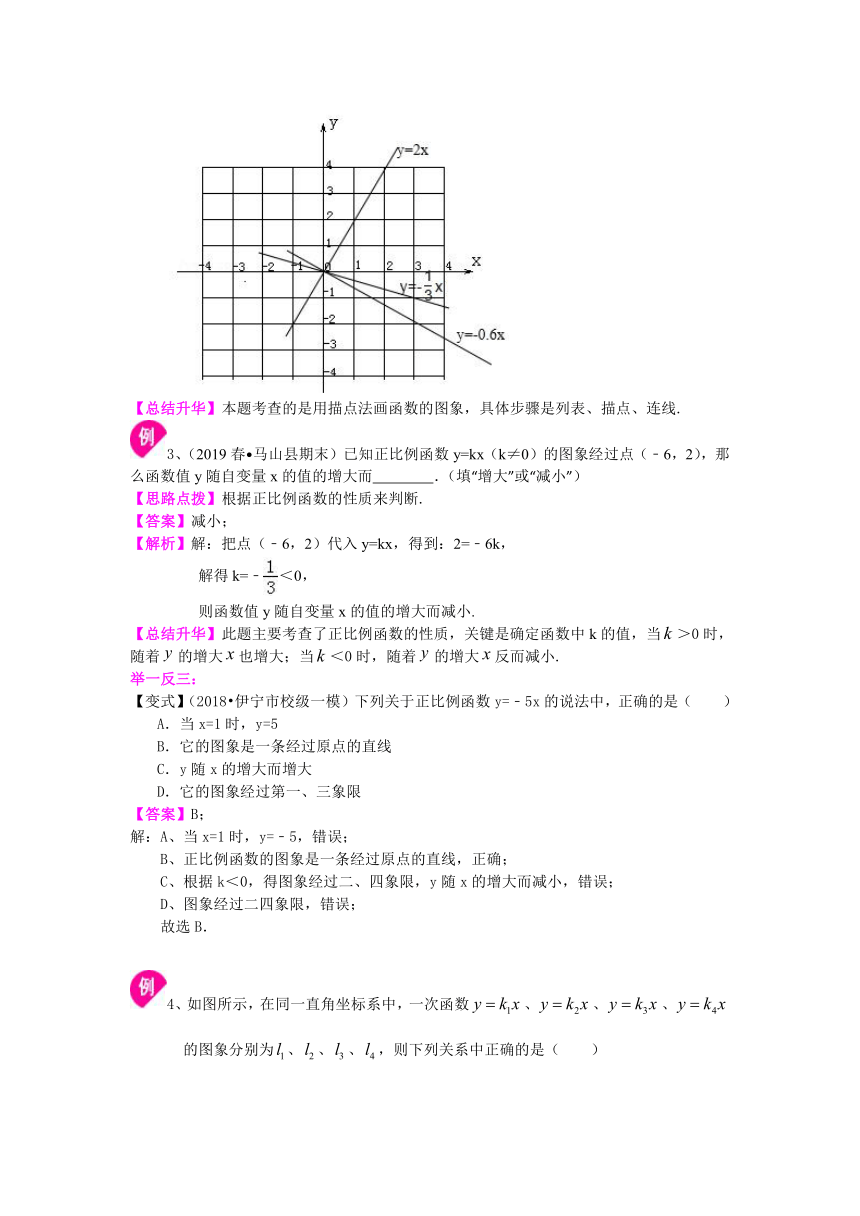
2、(2018秋?灵武市校级期中)在同一直角坐标系上画出函数y=2x,y=﹣x,y=﹣0.6x的图象.
【思路点拨】分别在每个函数图象上找出两点,画出图象,根据函数图象的特点进行解答即可.
【答案与解析】
解:列表:
描点,连线:
【总结升华】本题考查的是用描点法画函数的图象,具体步骤是列表、描点、连线.
3、(2019春?马山县期末)已知正比例函数y=kx(k≠0)的图象经过点(﹣6,2),那么函数值y随自变量x的值的增大而 .(填“增大”或“减小”)
【思路点拨】根据正比例函数的性质来判断.
【答案】减小;
【解析】解:把点(﹣6,2)代入y=kx,得到:2=﹣6k,
解得k=﹣<0,
则函数值y随自变量x的值的增大而减小.
【总结升华】此题主要考查了正比例函数的性质,关键是确定函数中k的值,当>0时,随着的增大也增大;当<0时,随着的增大反而减小.
举一反三:
【变式】(2018?伊宁市校级一模)下列关于正比例函数y=﹣5x的说法中,正确的是( )
A.当x=1时,y=5
B.它的图象是一条经过原点的直线
C.y随x的增大而增大
D.它的图象经过第一、三象限
【答案】B;
解:A、当x=1时,y=﹣5,错误;
B、正比例函数的图象是一条经过原点的直线,正确;
C、根据k<0,得图象经过二、四象限,y随x的增大而减小,错误;
D、图象经过二四象限,错误;
故选B.
4、如图所示,在同一直角坐标系中,一次函数、、、 的图象分别为、、、,则下列关系中正确的是( )
A.<<< B.<<<
C.<<< D.<<<
【答案】B;
【解析】首先根据直线经过的象限,知:<0,<0,>0,>0,再根据直线越陡,||越大,知:>||,||<||.则<<<
【总结升华】此题主要考查了正比例函数图象的性质,首先根据直线经过的象限判断的符号,再进一步根据直线的平缓趋势判断的绝对值的大小,最后判断四个数的大小.
类型三、正比函数应用
5、如图所示,射线、分别表示甲、乙两名运动员在自行车比赛中所走路程与时间的函数关系,则他们行进的速度关系是( ).
A.甲比乙快 B.乙比甲快 C.甲、乙同速 D.不一定
【思路点拨】观察图象,在t相同的情况下,有,故易判断甲乙的速度大小.
【答案】A;
【解析】由知,,观察图象,在相同的情况下,有,故有.
【总结升华】此问题中,、对应的解析式中,的绝对值越大,速度越快.
举一反三:
【变式】如图,OA,BA分别表示甲、乙两名学生运动的函数图象,图中和分别表示运动路程和时间,根据图象判断快者的速度比慢者的速度每秒快( )
A.2.5米 B.2米 C.1.5米 D.1米
【答案】C;
提示:从图中可以看出甲用了8秒钟跑了64米,速度是8米/秒,乙用了8秒钟跑了52米,速度是米/秒,所以快者的速度比慢者的速度每秒快1.5米.
【巩固练习】
一.选择题
1. 直线过点(0,0)和点( )
A.(-1,-3) B.(1,3) C.(1,-3) D.(3,-1)
2. 下列函数中,是正比例函数的是( )
A. B.
C. D.
3.(2018春?澧县期末)在下列各图象中,表示函数y=﹣kx(k<0)的图象的是( )
A. B. C. D.
4. 如图所示,直线的函数解析式是( ).
A. B. C. D.
5.(2019?江西模拟)关于函数y=2x,下列结论中正确的是( )
A.函数图象都经过点(2,1)
B.函数图象都经过第二、四象限
C.y随x的增大而增大
D.不论x取何值,总有y>0
6.点A(–5,)和B(–2,)都在直线上,则与的关系是( )
A. ≤ B. = C. < D. >
二.填空题
7.若直线经过点A(-4,3),则=______.如果这条直线上点A的横坐标=4,那么它的纵坐标=______.
8. 已知三角形底边长为4,高为,三角形的面积为,则与的函数关系式为_______________.
9. -2与+1成正比例,比例系数为-2,将表示成的函数为:___________.
10.(2018春?建瓯市校级月考)已知正比例函数y=(1﹣m)x|m﹣2|,且y随x的增大而减小,则m的值是 .
11. 若函数是正比例函数,那么=______,图象经过第_______象限.
12. (2019春?正定县期末)若函数y=(2m+6)x+(1﹣m)是正比例函数,则m的值是 .
三.解答题
13.蜡烛点燃后缩短长度()与燃烧时间(分钟)之间的关系为,已知长为21的蜡烛燃烧6分钟后,蜡烛缩短了3.6,求:
(1)与之间的函数解析式;
(2)此蜡烛几分钟燃烧完.
14.(2018春?衡阳县期中)已知y是x的正比例函数,且函数图象经过点A(﹣3,6).
(1)求y与x的函数关系式;
(2)当x=﹣6时,求对应的函数值y;
(3)当x取何值时,y=.
15.若正比例函数的图像经过点A(-5,3),
(1)求的值;
(2)判断随的增大如何变化;
(3)如果这条直线上点B的横坐标=4,那么它的纵坐标的值是多少?
【答案与解析】
一.选择题
1. 【答案】C;
【解析】正比例函数过原点和点(1,).
2. 【答案】A;
3. 【答案】C;
【解析】解:∵k<0,∴﹣k>0,
∴函数y=﹣kx(k<0)的值随自变量x的增大而增大,且函数为正比例函数,
故选:C.
4. 【答案】C;
【解析】由图知,的图象过点(-3,2),则2=-3,解得,故选C.
5. 【答案】C;
【解析】A、函数图象经过点(2,4),错误;B、函数图象经过第一、三象限,错误;
C、y随x的增大而增大,正确;D、当x>0时,才有y>0,错误;故选C.
6. 【答案】D;
【解析】<0,随着的增大而减小.
二.填空题
7. 【答案】;-3;
【解析】将点A的坐标代入,求.
8. 【答案】;
【解析】由题意.
9. 【答案】;
【解析】由题意可得:,化简得:.
10.【答案】3;
【解析】解:∵此函数是正比例函数,
∴,
解得m=3.
11.【答案】4,一、三
【解析】函数是正比例函数,可知-4=0,可以得出的值,即可得出函数关系式,比例系数为15>0,故图象过第一、三象限.
12.【答案】1;
【解析】∵函数y=(2m+6)x+(1﹣m)是正比例函数,∴,解得m=1.
三.解答题
13.【解析】
解:(1)由题意,3.6=6,解出=0.6
所以=0.6
(2)21=0.6,解得=35,所以此蜡烛35分钟燃烧.
14.【解析】
解:(1)设正比例函数解析式为y=kx,
∵图象经过点(﹣3,6),
∴﹣3k=6,
解得k=﹣2,
所以,此函数的关系式是y=﹣2x;
(2)把x=﹣6代入解析式可得:y=12;
(3)把y=代入解析式可得:x=﹣.
15.【解析】
解:(1)∵直线经过点A(-5,3)∴3=-5
∴= ∴直线的解析式为
(2)∵=<0,∴随的增大而减小。
(3)∵B点在直线上,=4,∴=.
【学习目标】
1. 理解正比例函数的概念,能正确画出正比例函数的图象;
2. 能依据图象说出正比例函数的主要性质,解决简单的实际问题.
【要点梳理】
要点一、正比例函数的定义
1、正比例函数的定义
一般的,形如 (为常数,且≠0)的函数,叫做正比例函数.其中叫做比例系数.
2、正比例函数的等价形式
(1)、是的正比例函数;
(2)、(为常数且≠0);
(3)、若与成正比例;
(4)、(为常数且≠0).
要点二、正比例函数的图象与性质
正比例函数(是常数,≠0)的图象是一条经过原点的直线,我们称它为直线.当>0时,直线经过第一、三象限,从左向右上升,即随着的增大也增大;当<0时,直线经过第二、四象限,从左向右下降,即随着的增大反而减小.
要点三、待定系数法求正比例函数的解析式
由于正比例函数(为常数,≠0 )中只有一个待定系数,故只要有一对,的值或一个非原点的点,就可以求得值.
【典型例题】
类型一、正比例函数的定义
1、已知,当为何值时,是的正比例函数?
【思路点拨】正比例函数的一般式为,要特别注意定义满足,的指数为1.
【答案与解析】
解:由题意得, 解得 =2
∴当=2时,是的一次函数.
【总结升华】理解正比例函数的概念应抓住解析式中的两个主要特征:(1)不等于零;(2)的指数是1.
举一反三:
【变式】如果函数是正比例函数,那么的值是________.
【答案】
解:由定义得 解得 ∴ =2.
类型二、正比函数的图象和性质
2、(2018秋?灵武市校级期中)在同一直角坐标系上画出函数y=2x,y=﹣x,y=﹣0.6x的图象.
【思路点拨】分别在每个函数图象上找出两点,画出图象,根据函数图象的特点进行解答即可.
【答案与解析】
解:列表:
描点,连线:
【总结升华】本题考查的是用描点法画函数的图象,具体步骤是列表、描点、连线.
3、(2019春?马山县期末)已知正比例函数y=kx(k≠0)的图象经过点(﹣6,2),那么函数值y随自变量x的值的增大而 .(填“增大”或“减小”)
【思路点拨】根据正比例函数的性质来判断.
【答案】减小;
【解析】解:把点(﹣6,2)代入y=kx,得到:2=﹣6k,
解得k=﹣<0,
则函数值y随自变量x的值的增大而减小.
【总结升华】此题主要考查了正比例函数的性质,关键是确定函数中k的值,当>0时,随着的增大也增大;当<0时,随着的增大反而减小.
举一反三:
【变式】(2018?伊宁市校级一模)下列关于正比例函数y=﹣5x的说法中,正确的是( )
A.当x=1时,y=5
B.它的图象是一条经过原点的直线
C.y随x的增大而增大
D.它的图象经过第一、三象限
【答案】B;
解:A、当x=1时,y=﹣5,错误;
B、正比例函数的图象是一条经过原点的直线,正确;
C、根据k<0,得图象经过二、四象限,y随x的增大而减小,错误;
D、图象经过二四象限,错误;
故选B.
4、如图所示,在同一直角坐标系中,一次函数、、、 的图象分别为、、、,则下列关系中正确的是( )
A.<<< B.<<<
C.<<< D.<<<
【答案】B;
【解析】首先根据直线经过的象限,知:<0,<0,>0,>0,再根据直线越陡,||越大,知:>||,||<||.则<<<
【总结升华】此题主要考查了正比例函数图象的性质,首先根据直线经过的象限判断的符号,再进一步根据直线的平缓趋势判断的绝对值的大小,最后判断四个数的大小.
类型三、正比函数应用
5、如图所示,射线、分别表示甲、乙两名运动员在自行车比赛中所走路程与时间的函数关系,则他们行进的速度关系是( ).
A.甲比乙快 B.乙比甲快 C.甲、乙同速 D.不一定
【思路点拨】观察图象,在t相同的情况下,有,故易判断甲乙的速度大小.
【答案】A;
【解析】由知,,观察图象,在相同的情况下,有,故有.
【总结升华】此问题中,、对应的解析式中,的绝对值越大,速度越快.
举一反三:
【变式】如图,OA,BA分别表示甲、乙两名学生运动的函数图象,图中和分别表示运动路程和时间,根据图象判断快者的速度比慢者的速度每秒快( )
A.2.5米 B.2米 C.1.5米 D.1米
【答案】C;
提示:从图中可以看出甲用了8秒钟跑了64米,速度是8米/秒,乙用了8秒钟跑了52米,速度是米/秒,所以快者的速度比慢者的速度每秒快1.5米.
【巩固练习】
一.选择题
1. 直线过点(0,0)和点( )
A.(-1,-3) B.(1,3) C.(1,-3) D.(3,-1)
2. 下列函数中,是正比例函数的是( )
A. B.
C. D.
3.(2018春?澧县期末)在下列各图象中,表示函数y=﹣kx(k<0)的图象的是( )
A. B. C. D.
4. 如图所示,直线的函数解析式是( ).
A. B. C. D.
5.(2019?江西模拟)关于函数y=2x,下列结论中正确的是( )
A.函数图象都经过点(2,1)
B.函数图象都经过第二、四象限
C.y随x的增大而增大
D.不论x取何值,总有y>0
6.点A(–5,)和B(–2,)都在直线上,则与的关系是( )
A. ≤ B. = C. < D. >
二.填空题
7.若直线经过点A(-4,3),则=______.如果这条直线上点A的横坐标=4,那么它的纵坐标=______.
8. 已知三角形底边长为4,高为,三角形的面积为,则与的函数关系式为_______________.
9. -2与+1成正比例,比例系数为-2,将表示成的函数为:___________.
10.(2018春?建瓯市校级月考)已知正比例函数y=(1﹣m)x|m﹣2|,且y随x的增大而减小,则m的值是 .
11. 若函数是正比例函数,那么=______,图象经过第_______象限.
12. (2019春?正定县期末)若函数y=(2m+6)x+(1﹣m)是正比例函数,则m的值是 .
三.解答题
13.蜡烛点燃后缩短长度()与燃烧时间(分钟)之间的关系为,已知长为21的蜡烛燃烧6分钟后,蜡烛缩短了3.6,求:
(1)与之间的函数解析式;
(2)此蜡烛几分钟燃烧完.
14.(2018春?衡阳县期中)已知y是x的正比例函数,且函数图象经过点A(﹣3,6).
(1)求y与x的函数关系式;
(2)当x=﹣6时,求对应的函数值y;
(3)当x取何值时,y=.
15.若正比例函数的图像经过点A(-5,3),
(1)求的值;
(2)判断随的增大如何变化;
(3)如果这条直线上点B的横坐标=4,那么它的纵坐标的值是多少?
【答案与解析】
一.选择题
1. 【答案】C;
【解析】正比例函数过原点和点(1,).
2. 【答案】A;
3. 【答案】C;
【解析】解:∵k<0,∴﹣k>0,
∴函数y=﹣kx(k<0)的值随自变量x的增大而增大,且函数为正比例函数,
故选:C.
4. 【答案】C;
【解析】由图知,的图象过点(-3,2),则2=-3,解得,故选C.
5. 【答案】C;
【解析】A、函数图象经过点(2,4),错误;B、函数图象经过第一、三象限,错误;
C、y随x的增大而增大,正确;D、当x>0时,才有y>0,错误;故选C.
6. 【答案】D;
【解析】<0,随着的增大而减小.
二.填空题
7. 【答案】;-3;
【解析】将点A的坐标代入,求.
8. 【答案】;
【解析】由题意.
9. 【答案】;
【解析】由题意可得:,化简得:.
10.【答案】3;
【解析】解:∵此函数是正比例函数,
∴,
解得m=3.
11.【答案】4,一、三
【解析】函数是正比例函数,可知-4=0,可以得出的值,即可得出函数关系式,比例系数为15>0,故图象过第一、三象限.
12.【答案】1;
【解析】∵函数y=(2m+6)x+(1﹣m)是正比例函数,∴,解得m=1.
三.解答题
13.【解析】
解:(1)由题意,3.6=6,解出=0.6
所以=0.6
(2)21=0.6,解得=35,所以此蜡烛35分钟燃烧.
14.【解析】
解:(1)设正比例函数解析式为y=kx,
∵图象经过点(﹣3,6),
∴﹣3k=6,
解得k=﹣2,
所以,此函数的关系式是y=﹣2x;
(2)把x=﹣6代入解析式可得:y=12;
(3)把y=代入解析式可得:x=﹣.
15.【解析】
解:(1)∵直线经过点A(-5,3)∴3=-5
∴= ∴直线的解析式为
(2)∵=<0,∴随的增大而减小。
(3)∵B点在直线上,=4,∴=.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
