人教版高中数学必修一知识讲解,巩固练习(教学资料,补习资料):专题2.2 对数函数
文档属性
| 名称 | 人教版高中数学必修一知识讲解,巩固练习(教学资料,补习资料):专题2.2 对数函数 |

|
|
| 格式 | zip | ||
| 文件大小 | 737.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-19 00:00:00 | ||
图片预览




文档简介
/
知识
一、对数
1.对数的概念
(1)对数:一般地,如果,那么数 x叫做以a为底 N的对数,记作_______,其中a叫做对数的底数,N叫做真数.
(2)常用对数:通常我们将以_______为底的对数叫做常用对数,并把记为lg N.
(3)自然对数:在科学技术中常使用以无理数e=2.718 28……为底数的对数,以e为底的对数称为自然对数,并把记为ln N.
2.对数与指数的关系
当a>0,且a≠1时,.即
/
3.对数的性质
根据对数的概念,知对数具有以下性质:
(1)负数和零没有对数,即;
(2)1的对数等于0,即;
(3)底数的对数等于1,即.
二、对数的运算
1.基本性质
若,则
(1)______;
(2)______.
2.对数的运算性质
如果,那么:
(1);
(2);
(3).
三、换底公式及公式的推广
1.对数的换底公式
.
【注】速记口诀:
换底公式真神奇,换成新底可任意,
原底加底变分母,真数加底变分子.
2.公式的推广
(1)(其中a>0且;b>0且);
(2)(其中a>0且;b>0);
(3)(其中a>0且;b>0);
(4)(其中a>0且;b>0);
(5)(其中a,b,c均大于0且不等于1,d>0).
四、对数函数
1.对数函数的概念
一般地,我们把函数叫做对数函数,其中x是自变量,函数的定义域是_____.
2.对数函数的结构特征
(1)对数符号前面的系数是1;
(2)对数的底数是不等于1的正实数(常数);
(3)对数的真数仅有自变量x.
五、对数函数的图象与性质
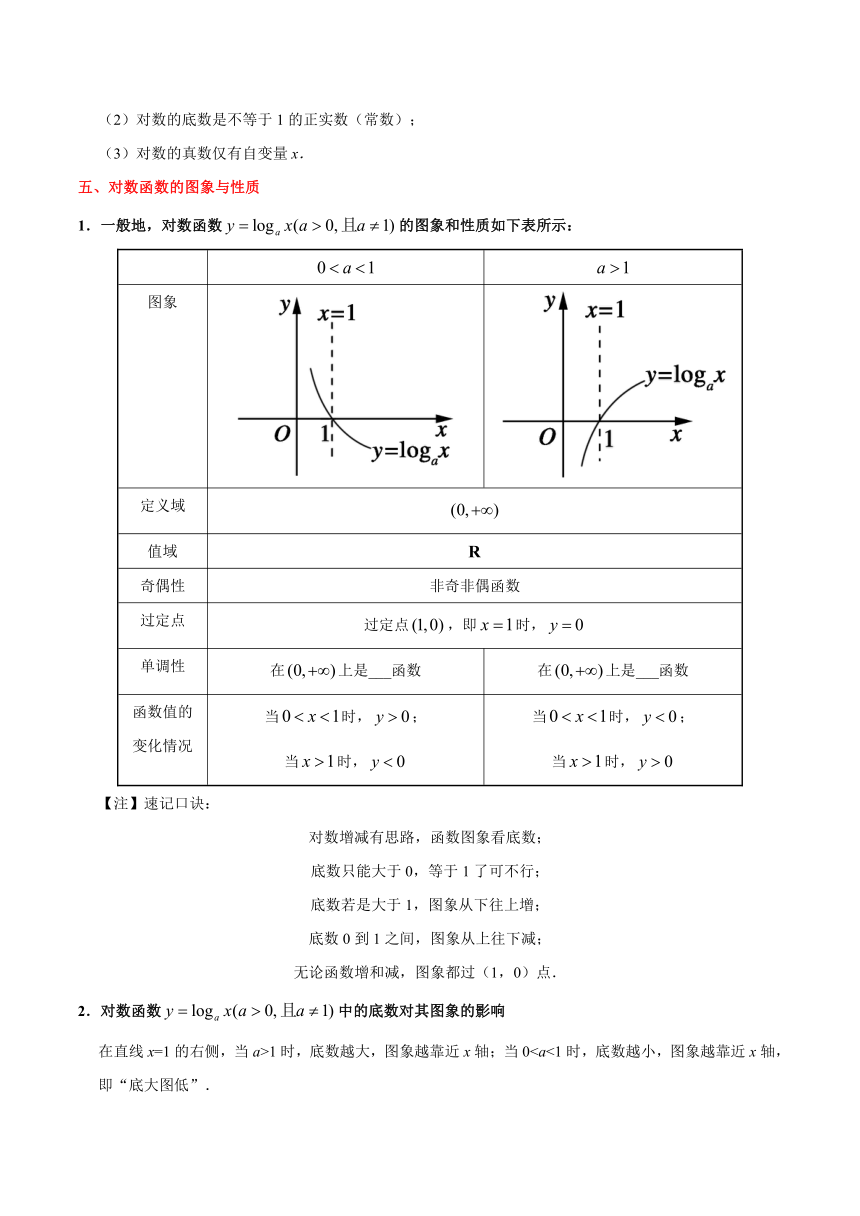
1.一般地,对数函数的图象和性质如下表所示:
图象
/
/
定义域
值域
奇偶性
非奇非偶函数
过定点
过定点,即时,
单调性
在上是___函数
在上是___函数
函数值的变化情况
当时,;
当时,
当时,;
当时,
【注】速记口诀:
对数增减有思路,函数图象看底数;
底数只能大于0,等于1了可不行;
底数若是大于1,图象从下往上增;
底数0到1之间,图象从上往下减;
无论函数增和减,图象都过(1,0)点.
2.对数函数中的底数对其图象的影响
在直线x=1的右侧,当a>1时,底数越大,图象越靠近x轴;当0六、反函数
根据指数与对数的关系,将指数式(其中是自变量,且,是的函数,)化成对数式,即,于是对于任意一个,通过式子都有唯一一个与之对应,这样将看成自变量,是的函数,这时我们就说是函数的反函数.
由于习惯上将看成自变量,而将看成因变量,因此,我们将中的,互换,写成,即对数函数是指数函数的反函数,它们的图象关于直线对称.
知识参考答案:
一、1.(1) (2)10
二、1.(1) (2)
2.(1) (2) (3)
四、1.
五、1.减 增
重点
重点
1.对数,对数的运算性质,换底公式;
2.对数函数的概念、对数函数的图象与性质.
难点
1.对数的运算性质;
2.对数型复合函数的性质及其应用.
易错
1.对于对数运算,不仅要注意“真数大于0”这一隐含条件,还应准确掌握对数的运算法则,保证对数运算的每一步都是等价的;
2.关于对数函数常见的易错点有三个:
(1)忽略对数函数定义域的限制;
(2)对于字母为底数的对数函数不加讨论;
(3)解有关对数函数的不等式时,忽略真数大于0这一基本条件,使解集扩大.
1.对数的概念
解决使对数式有意义的参数问题,只要注意满足底数和真数的条件,然后解不等式(组)即可.对数的概念是对数式和指数式互化的依据,在互化过程中应注意对数式和指数式之间的对应关系.
【例1】在对数式中,实数的取值范围应该是
A.11且x≠2
C.x>3 D.1【答案】D
/
【名师点睛】本题极易忽略底数的限制范围,底数需大于0且不等于1.
2.对数运算性质的应用
对数的运算性质是进行对数运算和化简的基础,所以要熟记对数的运算性质以及对数恒等式,化简的原则是:
(1)尽量将真数化为 “底数”一致的形式;
(2)将同底的多个对数的和(差)合成积(商)的对数;
(3)将积(商)的对数分成若干个对数的和(差).运算时要灵活运用对数的相关公式求解,如
,等.
【例2】计算:(1); (2).
【答案】(1);(2)1.
/
【名师点睛】在计算的值时,注意将化为即可求解.在求解(2)时,注意提取公因式,利用求解.
3.换底公式的应用
换底公式即将底数不同的对数转化为底数相同的对数,进而进行化简、计算或证明.换底公式应用时究竟换成什么为底,由已知条件来确定,一般换成以10为底的常用对数或以e为底的自然对数.
【例3】已知,试用表示.
【答案】.
【解析】.
∵∴.
则.
【名师点睛】在解题的方向还不清楚的情况下,一般统一为常用对数(当然也可以换成其他非1的正数为底).
4.对数方程的求解
解对数方程时,(1)等号两边为底数相同的对数式,则真数相等;(2)化简后得到关于简单对数式的一元二次方程,再由对数式与指数式的互化求解.
【例4】方程的解为 .
【答案】
/
【名师点睛】本题所给方程的底数相同,若底数不同,则还需化为同底数再求解.另外,解对数方程必须把所求得的解代入原方程进行检验,以确保所有的真数都大于零,这是必不可少的步骤.
5.与对数函数有关的函数的定义域和值域
定义域是使解析式有意义的自变量的取值集合,求与对数函数有关的定义域问题时,要注意对数函数的概念,若自变量在真数上,则必须保证真数大于0;若自变量在底数上,应保证底数大于0且不等于1.同时还要注意偶次方根的被开方数非负,分母不能为零等.
求值域时,一方面要抓住对数函数的定义域和单调性,另一方面,若是复合函数,则要抓住中间变量的取值范围.
【例5】已知函数.
(1)求函数的定义域;
(2)求函数的最大值.
【答案】(1);(2).
【解析】(1)由题意得,解得,
故函数的定义域是.
(2)=,.
令,则.
又在上为增函数,
∴的最大值是.
【名师点睛】求函数的最值,一定要坚持“定义域优先”的原则.由对数函数组成的复合函数的最值问题,可利用换元法求解,但要注意中间变量的取值范围.
6.对数函数的图象
对数函数的图象过定点(1,0),所以讨论与对数函数有关的函数的图象过定点的问题,只需令真数为1,解出相应的,即可得到定点的坐标.
当底数时,对数函数是上的增函数,当时,底数的值越小,函数图象越“陡”,其函数值增长得越快;当底数时,对数函数是上的减函数,当时,底数的值越大,函数图象越“陡”,其函数值减小得越快.也可作直线y=1与所给图象相交,交点的横坐标即为各个底数,依据在第一象限内,自左向右,图象对应的对数函数的底数逐渐变大,可比较底数的大小.
【例6】设,函数的图象恒过定点P,则P点的坐标是
A. B.
C. D.
【答案】A
/
【名师点睛】本题求定点坐标的依据是对数函数的图象过定点(1,0),不必分和两种情况讨论.
7.对数函数单调性的应用
(1)比较对数式的大小:若比较同底数的两个对数式的大小,可直接利用对数函数的单调性;若比较底数不同、真数相同的两个对数式的大小,可以先用换底公式化为同底后,再进行比较,也可以利用顺时针方向底数增大画出对数函数的图象,再进行比较;若比较底数与真数都不同的两个对数式的大小,常借助1,0等中间量进行比较.
(2)解简单的对数不等式:形如的不等式,常借助的单调性求解,如果的取值不确定,需分与两种情况进行讨论;形如的不等式,应将化为以为底数的对数式的形式,再借助的单调性求解.
【例7】已知,则
A. B.
C. D.
【答案】C
/
【名师点睛】本题中既有指数式,又有对数式,无法直接比较大小,可借助中间量1,0来进行比较.
8.对数型复合函数的性质及其应用
(1)对数复合函数的单调性
复合函数y=f[g(x)]是由y=f(x)与y=g(x)复合而成,若f(x)与g(x)的单调性相同,则其复合函数f[g(x)]为增函数;若f(x)与g(x)的单调性相反,则其复合函数f[g(x)]为减函数.
对于对数型复合函数y=logaf(x)来说,函数y=logaf(x)可看成是y=logau与u=f(x)两个简单函数复合而成的,由复合函数单调性“同增异减”的规律即可判断.另外,在求复合函数的单调性时,首先要考虑函数的定义域.
(2)对于形如y=logaf(x)(a>0,且a≠1)的复合函数,其值域的求解步骤如下:
①分解成y=logau,u=f(x)两个函数;
②求f(x)的定义域;
③求u的取值范围;
④利用y=logau的单调性求解.
【例8】讨论函数的单调性.
【答案】答案详见解析.
【解析】由3x2?2x?1>0,得函数的定义域为{x|x>1或x<}.
①当a>1时,
若x>1,∵u=3x2?2x?1为增函数,
∴f(x)=loga(3x2?2x?1)为增函数.
若x<,∵u=3x2?2x?1为减函数,
∴f(x)=loga(3x2?2x?1)为减函数.
②当0若x>1,则f(x)=loga(3x2?2x?1)为减函数,
若x<,则f(x)=loga(3x2?2x?1)为增函数.
【名师点睛】求复合函数单调性的具体步骤是:(1)求定义域;(2)拆分函数;(3)分别求y=f(u),u=φ(x)的单调性;(4)按“同增异减”得出复合函数的单调性.
9.K易错——忽略真数大于0
【例9】已知,求的值.
【错解】因为,
所以,即,即,解得或.
所以或.
【错因分析】错解中,与对的取值范围要求是不同的,即求解过程不等价,因此,得出解后要代入原方程验证.
【正解】同错解,得到或.
由知,,
当时,,此时无意义,所以,
即应舍去;
当时,.
【名师点睛】求解有关对数恒等式或不等式的过程中,经常需要将对数符号“脱掉”,此时很容易忽略原式中对数的真数大于0这一隐性限制条件,从而导致求出的最终结果中产生增根或范围扩大,因此要求我们对于此类题,一定要将求出的结果代入原式中进行检验.
10.K易错——忽略对底数的讨论
【例10】不等式的解集是_______.
【错解】∵,
∴原不等式等价于,
∴,解得x<2.
∴不等式的解集为.
【错因分析】错解中的底数的值不确定,因此要分类讨论.另外,求解时要保证真数大于0.
/
【名师点睛】解对数不等式时,要防止定义域扩大,途径有两种:一是不同解变形,最后一定要检验;二是解的过程中加上限制条件,如正解,使定义域保持不变,即进行同解变形,最后通过解不等式组得到原不等式的解,这样得出的解就不用检验了.
基础训练
1.等于
A.1 B.2 C.5 D.6
2.实数的值为
A.1 B.2 C.3 D.4
3.已知函数f(x)=log2(3+x)+log2(3–x),则f(1)=
A.1 B.log26
C.3 D.log29
4.若,则有
A.a=2b B.b=2a
C.a=4b D.b=4a
5.设,则f(3)的值是
A.128 B.256
C.512 D.8
6.log5+log53等于
A.0 B.1
C.–1 D.log5
7.若a=,b=,c=log23,则a,b,c大小关系是
A.aC.b8.若a=30.4,b=0.43,c=log0.43,则
A.bC.a9.若且abc≠0,则=
A.2 B.1 C.3 D.4
10.已知,则下列不等式一定成立的是
A. B.
C.ln(a–b)>0 D.3a–b<1
11.函数的定义域为__________.
12.函数y=lgx的反函数是__________.
13.函数f(x)=的定义域为__________.
14.设2x=5y=m,且=2,则m的值是__________.
15.方程log2(2–x)+log2(3–x)=log212的解x=__________.
能力提升
16.已知f(x)=lg(10+x)+lg(10–x),则f(x)是
A.f(x)是奇函数,且在(0,10)是增函数
B.f(x)是偶函数,且在(0,10)是增函数
C.f(x)是奇函数,且在(0,10)是减函数
D.f(x)是偶函数,且在(0,10)是减函数
17.设正实数a,b满足6a=2b,则
A.0 B.1
C.2 D.3
18.根据有关资料,围棋状态空间复杂度的上限M约为3361,而可观测宇宙中普通物质的原子总数N为1080,则下列各数中与最接近的是
A.1033 B.1053
C.1073 D.1093
19.若log2(log3a)=log3(log4b)=log4(log2c)=1,则a,b,c的大小关系是
A.a>b>c B.b>a>c
C.a>c>b D.b>c>a
20.若正实数x,y满足log2(x+3y)=log4x2+log2(2y),则x+3y的最小值是
A.12 B.10
C.8 D.6
21.对任意的正实数x,y,下列等式不成立的是
A.lgy–lgx=lg B.lg(x+y)=lgx+lgy
C.lgx3=3lgx D.lgx=
22.设函数y=f(x)的图象与y=log2(x+a)的图象关于直线y=–x对称,且f(–2)+f(–1)=2,则a=
A.3 B.1 C.2 D.4
23.已知函数f(x)=ln(–x2–2x+3),则f(x)的增区间为
A.(–∞,–1) B.(–3,–1)
C.[–1,+∞) D.[–1,1)
24.已知函数,则函数f(x)的减区间是
A.(–∞,2) B.(2,+∞)
C.(5,+∞) D.(–∞,–1)
25.已知R上的奇函数f(x)满足当x<0时,f(x)=log2(1–x),则f(f(1))=
A.–1 B.–2
C.1 D.2
26.若实数a,b满足a>b>1,m=loga(logab),,,则m,n,l的大小关系为
A.m>l>n B.l>n>m
C.n>l>m D.l>m>n
27.函数f(x)=loga(3–ax)(a>0且a≠1)在区间(a–2,a)上单调递减,则a的取值范围为__________.
28.已知函数f(x)=a?2x+3–a(a∈R)的反函数为y=f–1(x),则函数y=f–1(x)的图象经过的定点的坐标为__________.
29.若函数f(x)=loga(x2–ax+1)(a>0且a≠1)没有最小值,则a的取值范围是__________.
30.(1);
(2).
31.求函数f(x)=log(x2–3)的单调区间.
32.已知函数f(x)=lg(x+1)–lg(1–x).
(1)求函数f(x)的定义域;
(2)判断函数f(x)的奇偶性.
33.已知函数f(x)=loga(1+x)–loga(1–x),其中a>0且a≠1.
(1)求函数f(x)的定义域;
(2)判断f(x)的奇偶性,并说明理由;
(3)若f()=2,求使f(x)>0成立的x的集合.
真题练习
34.(2018?天津模拟)已知a=log2e,b=ln2,c=,则a,b,c的大小关系为
A.a>b>c B.b>a>c
C.c>b>a D.c>a>b
35.(2019?天津模拟)已知a=log3,b=,c=,则a,b,c的大小关系为
A.a>b>c B.b>a>c
C.c>b>a D.c>a>b
36.(2018?新课标Ⅲ)设a=log0.20.3,b=log20.3,则
A.a+bC.a+b<037.(2019?上海)设常数a∈R,函数f(x)=1og2(x+a).若f(x)的反函数的图象经过点(3,1),则a=__________.
38.【2018年全国卷Ⅲ文】已知函数,,则__________.
参考答案
1
2
3
4
5
6
7
8
9
10
16
17
B
C
C
C
B
A
A
D
A
A
D
C
18
19
20
21
22
23
24
25
26
34
35
36
D
D
D
B
D
B
C
C
B
D
D
B
1.【答案】B
【解析】原式==2.故选B.
2.【答案】C
【解析】=1+lg4+lg25=1+lg100=3.故选C.
3.【答案】C
【解析】f(1)=log24+log22=2+1=3.故选C.
4.【答案】C
【解析】,得,即a=4b.故选C.
5.【答案】B
【解析】设log2x=t,则x=2t,所以f(t)=,即f(x)=.则f(3)=.故选B.
6.【答案】A
【解析】原式==log51=0.故选A.
7.【答案】A
【解析】∵a=1,则a8.【答案】D
【解析】a=30.4>1,b=0.43∈(0,1),c=log0.43<0,则c9.【答案】A
/
10.【答案】A
【解析】∵,∴a>b>0,∴,,ln(a–b)与0的大小关系不确定,3a–b>1.因此只有A正确.故选A.
11.【答案】(–1,+∞)
【解析】应该满足,即2+x>1,解得x>–1,所以函数的定义域为(–1,+∞).故答案为:(–1,+∞).
12.【答案】y=10x
【解析】函数y=lgx,可得x=10y,所以函数y=lgx的反函数是y=10x.故答案为:y=10x.
13.【答案】(0,e]
【解析】函数的定义域为:{x|},解得014.【答案】
【解析】由2x=5y=m,得x=log2m,y=log5m,由=2,得,即logm2+logm5=2,∴logm10=2,∴m=.故答案为:.
15.【答案】–1
/
16.【答案】D
【解析】由得:x∈(–10,10),故函数f(x)的定义域为(–10,10),关于原点对称,又由f(–x)=lg(10–x)+lg(10+x)=f(x),故函数f(x)为偶函数,而f(x)=lg(10+x)+lg(10–x)=lg(100–x2),y=100–x2在(0,10)递减,y=lgx在(0,10)递增,故函数f(x)在(0,10)递减,故选D.
17.【答案】C
【解析】∵6a=2b,∴aln6=bln2,∴=1+=1+log23,∵118.【答案】D
【解析】由题意:M≈3361,N≈1080,根据对数性质有:3=10lg3≈100.48,∴M≈3361≈(100.48)361≈10173,
∴≈=1093.故选D.
19.【答案】D
【解析】由log2(log3a)=1,可得log3a=2,lga=2lg3,故a=32=9,由log3(log4b)=1,可得log4b=3,lgb=3lg4,故b=43=64,由log4(log2c)=1,可得log2c=4,lgc=4lg2,故c=24=16,∴b>c>a.故选D.
20.【答案】D
【解析】∵log2(x+3y)=log4x2+log2(2y),∴log2(x+3y)=log2x+log2(2y),即x+3y=2yx.可得:x+3y=?3yx.∴(x+3y),当且仅当x=3y时取等.令x+3y=t,(t>0),则6t≤t2,解得:t≥6,即x+3y≥6.故选D.
21.【答案】B
/
22.【答案】D
【解析】函数y=f(x)的图象与y=log2(x+a)的图象关于直线y=–x对称,设f(x)上任意一点为(x,y),则(x,y)关于直线y=–x对称的点为(–y,–x),把(–y,–x)代入y=log2(x+a),得–x=log2(–y+a),∴f(x)=–2–x+a,∵f(–2)+f(–1)=2,∴–22+a–2+a=2,解得a=4.故选D.
23.【答案】B
【解析】由–x2–2x+3>0,解得:–324.【答案】C
【解析】设t=x2–4x–5,由t>0可得x>5或x<–1,则y=t在(0,+∞)递减,由t=x2–4x–5在(5,+∞)递增,可得函数f(x)的减区间为(5,+∞).故选C.
25.【答案】C
【解析】设x>0,–x<0,f(x)为R上的奇函数,且x<0时,f(x)=log2(1–x),则f(–x)=log2(1+x)=–f(x),∴f(x)=–log2(1+x),∴f(1)=–1,∴f(f(1))=f(–1)=log22=1.故选C.
26.【答案】B
【解析】∵实数a,b满足a>b>1,m=loga(logab),,,∴0=loga1=2logab>.∴m,n,l的大小关系为l>n>m.故选B.
27.【答案】{a|1【解析】∵函数f(x)=loga(3–ax)(a>0且a≠1)在区间(a–2,a)上单调递减,∴,求得128.【答案】(3,0)
【解析】∵f(x)=a?2x+3–a=a(2x–1)+3过定点(0,3),∴f(x),的反函数y=f–1(x)的图象经过定点(3,0).故答案为:(3,0).
29.【答案】(0,1)∪[2,+∞)
/
30.【答案】(1)–7;(2).
【解析】(1)原式=
=log39–9=2–9=–7;
(2)
.
31.【答案】单减区间是(,+∞),单增区间是(–∞,–).
【解析】要使函数有意义,当且仅当u=x2–3>0,
即x>或x<–.
又x∈(,+∞)时,u是x的增函数;
x∈(–∞,–)时,u是x的减函数.
而u>0时,y=logu是减函数,
故函数y=log(x2–3)的单减区间是(,+∞),单增区间是(–∞,–).
32.【答案】(1)(–1,1);(2)f(x)为奇函数.
【解析】(1)要使原函数有意义,需满足,
解得–1故函数的定义域为(–1,1);
(2)∵f(–x)=lg(1–x)–lg(1+x)=–f(x)
∴f(x)为奇函数.
33.【答案】(1)(–1,1)(2)奇函数,理由详见解析;(3)(0,1).
/
(3)若f()=2,
∴loga(1+)–loga(1–)=loga4=2,
解得a=2,
∴f(x)=log2(1+x)–log2(1–x),
若f(x)>0,则log2(x+1)>log2(1–x),
∴x+1>1–x>0,
解得0故不等式的解集为(0,1).
34.【答案】D
【解析】a=log2e>1,0log2e=a,则a,b,c的大小关系c>a>b,故选D.
35.【答案】D
【解析】∵a=log3,c==log35,且5,∴,则b=,∴c>a>b.故选D.
36.【答案】B
/
37.【答案】7
【解析】∵常数a∈R,函数f(x)=1og2(x+a).f(x)的反函数的图象经过点(3,1),∴函数f(x)=1og2(x+a)的图象经过点(1,3),∴log2(1+a)=3,解得a=7.故答案为:7.
38.【答案】
【解析】,
∴,则,故答案为:–2.
知识
一、对数
1.对数的概念
(1)对数:一般地,如果,那么数 x叫做以a为底 N的对数,记作_______,其中a叫做对数的底数,N叫做真数.
(2)常用对数:通常我们将以_______为底的对数叫做常用对数,并把记为lg N.
(3)自然对数:在科学技术中常使用以无理数e=2.718 28……为底数的对数,以e为底的对数称为自然对数,并把记为ln N.
2.对数与指数的关系
当a>0,且a≠1时,.即
/
3.对数的性质
根据对数的概念,知对数具有以下性质:
(1)负数和零没有对数,即;
(2)1的对数等于0,即;
(3)底数的对数等于1,即.
二、对数的运算
1.基本性质
若,则
(1)______;
(2)______.
2.对数的运算性质
如果,那么:
(1);
(2);
(3).
三、换底公式及公式的推广
1.对数的换底公式
.
【注】速记口诀:
换底公式真神奇,换成新底可任意,
原底加底变分母,真数加底变分子.
2.公式的推广
(1)(其中a>0且;b>0且);
(2)(其中a>0且;b>0);
(3)(其中a>0且;b>0);
(4)(其中a>0且;b>0);
(5)(其中a,b,c均大于0且不等于1,d>0).
四、对数函数
1.对数函数的概念
一般地,我们把函数叫做对数函数,其中x是自变量,函数的定义域是_____.
2.对数函数的结构特征
(1)对数符号前面的系数是1;
(2)对数的底数是不等于1的正实数(常数);
(3)对数的真数仅有自变量x.
五、对数函数的图象与性质
1.一般地,对数函数的图象和性质如下表所示:
图象
/
/
定义域
值域
奇偶性
非奇非偶函数
过定点
过定点,即时,
单调性
在上是___函数
在上是___函数
函数值的变化情况
当时,;
当时,
当时,;
当时,
【注】速记口诀:
对数增减有思路,函数图象看底数;
底数只能大于0,等于1了可不行;
底数若是大于1,图象从下往上增;
底数0到1之间,图象从上往下减;
无论函数增和减,图象都过(1,0)点.
2.对数函数中的底数对其图象的影响
在直线x=1的右侧,当a>1时,底数越大,图象越靠近x轴;当0
根据指数与对数的关系,将指数式(其中是自变量,且,是的函数,)化成对数式,即,于是对于任意一个,通过式子都有唯一一个与之对应,这样将看成自变量,是的函数,这时我们就说是函数的反函数.
由于习惯上将看成自变量,而将看成因变量,因此,我们将中的,互换,写成,即对数函数是指数函数的反函数,它们的图象关于直线对称.
知识参考答案:
一、1.(1) (2)10
二、1.(1) (2)
2.(1) (2) (3)
四、1.
五、1.减 增
重点
重点
1.对数,对数的运算性质,换底公式;
2.对数函数的概念、对数函数的图象与性质.
难点
1.对数的运算性质;
2.对数型复合函数的性质及其应用.
易错
1.对于对数运算,不仅要注意“真数大于0”这一隐含条件,还应准确掌握对数的运算法则,保证对数运算的每一步都是等价的;
2.关于对数函数常见的易错点有三个:
(1)忽略对数函数定义域的限制;
(2)对于字母为底数的对数函数不加讨论;
(3)解有关对数函数的不等式时,忽略真数大于0这一基本条件,使解集扩大.
1.对数的概念
解决使对数式有意义的参数问题,只要注意满足底数和真数的条件,然后解不等式(组)即可.对数的概念是对数式和指数式互化的依据,在互化过程中应注意对数式和指数式之间的对应关系.
【例1】在对数式中,实数的取值范围应该是
A.1
C.x>3 D.1
/
【名师点睛】本题极易忽略底数的限制范围,底数需大于0且不等于1.
2.对数运算性质的应用
对数的运算性质是进行对数运算和化简的基础,所以要熟记对数的运算性质以及对数恒等式,化简的原则是:
(1)尽量将真数化为 “底数”一致的形式;
(2)将同底的多个对数的和(差)合成积(商)的对数;
(3)将积(商)的对数分成若干个对数的和(差).运算时要灵活运用对数的相关公式求解,如
,等.
【例2】计算:(1); (2).
【答案】(1);(2)1.
/
【名师点睛】在计算的值时,注意将化为即可求解.在求解(2)时,注意提取公因式,利用求解.
3.换底公式的应用
换底公式即将底数不同的对数转化为底数相同的对数,进而进行化简、计算或证明.换底公式应用时究竟换成什么为底,由已知条件来确定,一般换成以10为底的常用对数或以e为底的自然对数.
【例3】已知,试用表示.
【答案】.
【解析】.
∵∴.
则.
【名师点睛】在解题的方向还不清楚的情况下,一般统一为常用对数(当然也可以换成其他非1的正数为底).
4.对数方程的求解
解对数方程时,(1)等号两边为底数相同的对数式,则真数相等;(2)化简后得到关于简单对数式的一元二次方程,再由对数式与指数式的互化求解.
【例4】方程的解为 .
【答案】
/
【名师点睛】本题所给方程的底数相同,若底数不同,则还需化为同底数再求解.另外,解对数方程必须把所求得的解代入原方程进行检验,以确保所有的真数都大于零,这是必不可少的步骤.
5.与对数函数有关的函数的定义域和值域
定义域是使解析式有意义的自变量的取值集合,求与对数函数有关的定义域问题时,要注意对数函数的概念,若自变量在真数上,则必须保证真数大于0;若自变量在底数上,应保证底数大于0且不等于1.同时还要注意偶次方根的被开方数非负,分母不能为零等.
求值域时,一方面要抓住对数函数的定义域和单调性,另一方面,若是复合函数,则要抓住中间变量的取值范围.
【例5】已知函数.
(1)求函数的定义域;
(2)求函数的最大值.
【答案】(1);(2).
【解析】(1)由题意得,解得,
故函数的定义域是.
(2)=,.
令,则.
又在上为增函数,
∴的最大值是.
【名师点睛】求函数的最值,一定要坚持“定义域优先”的原则.由对数函数组成的复合函数的最值问题,可利用换元法求解,但要注意中间变量的取值范围.
6.对数函数的图象
对数函数的图象过定点(1,0),所以讨论与对数函数有关的函数的图象过定点的问题,只需令真数为1,解出相应的,即可得到定点的坐标.
当底数时,对数函数是上的增函数,当时,底数的值越小,函数图象越“陡”,其函数值增长得越快;当底数时,对数函数是上的减函数,当时,底数的值越大,函数图象越“陡”,其函数值减小得越快.也可作直线y=1与所给图象相交,交点的横坐标即为各个底数,依据在第一象限内,自左向右,图象对应的对数函数的底数逐渐变大,可比较底数的大小.
【例6】设,函数的图象恒过定点P,则P点的坐标是
A. B.
C. D.
【答案】A
/
【名师点睛】本题求定点坐标的依据是对数函数的图象过定点(1,0),不必分和两种情况讨论.
7.对数函数单调性的应用
(1)比较对数式的大小:若比较同底数的两个对数式的大小,可直接利用对数函数的单调性;若比较底数不同、真数相同的两个对数式的大小,可以先用换底公式化为同底后,再进行比较,也可以利用顺时针方向底数增大画出对数函数的图象,再进行比较;若比较底数与真数都不同的两个对数式的大小,常借助1,0等中间量进行比较.
(2)解简单的对数不等式:形如的不等式,常借助的单调性求解,如果的取值不确定,需分与两种情况进行讨论;形如的不等式,应将化为以为底数的对数式的形式,再借助的单调性求解.
【例7】已知,则
A. B.
C. D.
【答案】C
/
【名师点睛】本题中既有指数式,又有对数式,无法直接比较大小,可借助中间量1,0来进行比较.
8.对数型复合函数的性质及其应用
(1)对数复合函数的单调性
复合函数y=f[g(x)]是由y=f(x)与y=g(x)复合而成,若f(x)与g(x)的单调性相同,则其复合函数f[g(x)]为增函数;若f(x)与g(x)的单调性相反,则其复合函数f[g(x)]为减函数.
对于对数型复合函数y=logaf(x)来说,函数y=logaf(x)可看成是y=logau与u=f(x)两个简单函数复合而成的,由复合函数单调性“同增异减”的规律即可判断.另外,在求复合函数的单调性时,首先要考虑函数的定义域.
(2)对于形如y=logaf(x)(a>0,且a≠1)的复合函数,其值域的求解步骤如下:
①分解成y=logau,u=f(x)两个函数;
②求f(x)的定义域;
③求u的取值范围;
④利用y=logau的单调性求解.
【例8】讨论函数的单调性.
【答案】答案详见解析.
【解析】由3x2?2x?1>0,得函数的定义域为{x|x>1或x<}.
①当a>1时,
若x>1,∵u=3x2?2x?1为增函数,
∴f(x)=loga(3x2?2x?1)为增函数.
若x<,∵u=3x2?2x?1为减函数,
∴f(x)=loga(3x2?2x?1)为减函数.
②当0
若x<,则f(x)=loga(3x2?2x?1)为增函数.
【名师点睛】求复合函数单调性的具体步骤是:(1)求定义域;(2)拆分函数;(3)分别求y=f(u),u=φ(x)的单调性;(4)按“同增异减”得出复合函数的单调性.
9.K易错——忽略真数大于0
【例9】已知,求的值.
【错解】因为,
所以,即,即,解得或.
所以或.
【错因分析】错解中,与对的取值范围要求是不同的,即求解过程不等价,因此,得出解后要代入原方程验证.
【正解】同错解,得到或.
由知,,
当时,,此时无意义,所以,
即应舍去;
当时,.
【名师点睛】求解有关对数恒等式或不等式的过程中,经常需要将对数符号“脱掉”,此时很容易忽略原式中对数的真数大于0这一隐性限制条件,从而导致求出的最终结果中产生增根或范围扩大,因此要求我们对于此类题,一定要将求出的结果代入原式中进行检验.
10.K易错——忽略对底数的讨论
【例10】不等式的解集是_______.
【错解】∵,
∴原不等式等价于,
∴,解得x<2.
∴不等式的解集为.
【错因分析】错解中的底数的值不确定,因此要分类讨论.另外,求解时要保证真数大于0.
/
【名师点睛】解对数不等式时,要防止定义域扩大,途径有两种:一是不同解变形,最后一定要检验;二是解的过程中加上限制条件,如正解,使定义域保持不变,即进行同解变形,最后通过解不等式组得到原不等式的解,这样得出的解就不用检验了.
基础训练
1.等于
A.1 B.2 C.5 D.6
2.实数的值为
A.1 B.2 C.3 D.4
3.已知函数f(x)=log2(3+x)+log2(3–x),则f(1)=
A.1 B.log26
C.3 D.log29
4.若,则有
A.a=2b B.b=2a
C.a=4b D.b=4a
5.设,则f(3)的值是
A.128 B.256
C.512 D.8
6.log5+log53等于
A.0 B.1
C.–1 D.log5
7.若a=,b=,c=log23,则a,b,c大小关系是
A.a
A.b
A.2 B.1 C.3 D.4
10.已知,则下列不等式一定成立的是
A. B.
C.ln(a–b)>0 D.3a–b<1
11.函数的定义域为__________.
12.函数y=lgx的反函数是__________.
13.函数f(x)=的定义域为__________.
14.设2x=5y=m,且=2,则m的值是__________.
15.方程log2(2–x)+log2(3–x)=log212的解x=__________.
能力提升
16.已知f(x)=lg(10+x)+lg(10–x),则f(x)是
A.f(x)是奇函数,且在(0,10)是增函数
B.f(x)是偶函数,且在(0,10)是增函数
C.f(x)是奇函数,且在(0,10)是减函数
D.f(x)是偶函数,且在(0,10)是减函数
17.设正实数a,b满足6a=2b,则
A.0 B.1
C.2 D.3
18.根据有关资料,围棋状态空间复杂度的上限M约为3361,而可观测宇宙中普通物质的原子总数N为1080,则下列各数中与最接近的是
A.1033 B.1053
C.1073 D.1093
19.若log2(log3a)=log3(log4b)=log4(log2c)=1,则a,b,c的大小关系是
A.a>b>c B.b>a>c
C.a>c>b D.b>c>a
20.若正实数x,y满足log2(x+3y)=log4x2+log2(2y),则x+3y的最小值是
A.12 B.10
C.8 D.6
21.对任意的正实数x,y,下列等式不成立的是
A.lgy–lgx=lg B.lg(x+y)=lgx+lgy
C.lgx3=3lgx D.lgx=
22.设函数y=f(x)的图象与y=log2(x+a)的图象关于直线y=–x对称,且f(–2)+f(–1)=2,则a=
A.3 B.1 C.2 D.4
23.已知函数f(x)=ln(–x2–2x+3),则f(x)的增区间为
A.(–∞,–1) B.(–3,–1)
C.[–1,+∞) D.[–1,1)
24.已知函数,则函数f(x)的减区间是
A.(–∞,2) B.(2,+∞)
C.(5,+∞) D.(–∞,–1)
25.已知R上的奇函数f(x)满足当x<0时,f(x)=log2(1–x),则f(f(1))=
A.–1 B.–2
C.1 D.2
26.若实数a,b满足a>b>1,m=loga(logab),,,则m,n,l的大小关系为
A.m>l>n B.l>n>m
C.n>l>m D.l>m>n
27.函数f(x)=loga(3–ax)(a>0且a≠1)在区间(a–2,a)上单调递减,则a的取值范围为__________.
28.已知函数f(x)=a?2x+3–a(a∈R)的反函数为y=f–1(x),则函数y=f–1(x)的图象经过的定点的坐标为__________.
29.若函数f(x)=loga(x2–ax+1)(a>0且a≠1)没有最小值,则a的取值范围是__________.
30.(1);
(2).
31.求函数f(x)=log(x2–3)的单调区间.
32.已知函数f(x)=lg(x+1)–lg(1–x).
(1)求函数f(x)的定义域;
(2)判断函数f(x)的奇偶性.
33.已知函数f(x)=loga(1+x)–loga(1–x),其中a>0且a≠1.
(1)求函数f(x)的定义域;
(2)判断f(x)的奇偶性,并说明理由;
(3)若f()=2,求使f(x)>0成立的x的集合.
真题练习
34.(2018?天津模拟)已知a=log2e,b=ln2,c=,则a,b,c的大小关系为
A.a>b>c B.b>a>c
C.c>b>a D.c>a>b
35.(2019?天津模拟)已知a=log3,b=,c=,则a,b,c的大小关系为
A.a>b>c B.b>a>c
C.c>b>a D.c>a>b
36.(2018?新课标Ⅲ)设a=log0.20.3,b=log20.3,则
A.a+b
38.【2018年全国卷Ⅲ文】已知函数,,则__________.
参考答案
1
2
3
4
5
6
7
8
9
10
16
17
B
C
C
C
B
A
A
D
A
A
D
C
18
19
20
21
22
23
24
25
26
34
35
36
D
D
D
B
D
B
C
C
B
D
D
B
1.【答案】B
【解析】原式==2.故选B.
2.【答案】C
【解析】=1+lg4+lg25=1+lg100=3.故选C.
3.【答案】C
【解析】f(1)=log24+log22=2+1=3.故选C.
4.【答案】C
【解析】,得,即a=4b.故选C.
5.【答案】B
【解析】设log2x=t,则x=2t,所以f(t)=,即f(x)=.则f(3)=.故选B.
6.【答案】A
【解析】原式==log51=0.故选A.
7.【答案】A
【解析】∵a=
【解析】a=30.4>1,b=0.43∈(0,1),c=log0.43<0,则c
/
10.【答案】A
【解析】∵,∴a>b>0,∴,,ln(a–b)与0的大小关系不确定,3a–b>1.因此只有A正确.故选A.
11.【答案】(–1,+∞)
【解析】应该满足,即2+x>1,解得x>–1,所以函数的定义域为(–1,+∞).故答案为:(–1,+∞).
12.【答案】y=10x
【解析】函数y=lgx,可得x=10y,所以函数y=lgx的反函数是y=10x.故答案为:y=10x.
13.【答案】(0,e]
【解析】函数的定义域为:{x|},解得0
【解析】由2x=5y=m,得x=log2m,y=log5m,由=2,得,即logm2+logm5=2,∴logm10=2,∴m=.故答案为:.
15.【答案】–1
/
16.【答案】D
【解析】由得:x∈(–10,10),故函数f(x)的定义域为(–10,10),关于原点对称,又由f(–x)=lg(10–x)+lg(10+x)=f(x),故函数f(x)为偶函数,而f(x)=lg(10+x)+lg(10–x)=lg(100–x2),y=100–x2在(0,10)递减,y=lgx在(0,10)递增,故函数f(x)在(0,10)递减,故选D.
17.【答案】C
【解析】∵6a=2b,∴aln6=bln2,∴=1+=1+log23,∵1
【解析】由题意:M≈3361,N≈1080,根据对数性质有:3=10lg3≈100.48,∴M≈3361≈(100.48)361≈10173,
∴≈=1093.故选D.
19.【答案】D
【解析】由log2(log3a)=1,可得log3a=2,lga=2lg3,故a=32=9,由log3(log4b)=1,可得log4b=3,lgb=3lg4,故b=43=64,由log4(log2c)=1,可得log2c=4,lgc=4lg2,故c=24=16,∴b>c>a.故选D.
20.【答案】D
【解析】∵log2(x+3y)=log4x2+log2(2y),∴log2(x+3y)=log2x+log2(2y),即x+3y=2yx.可得:x+3y=?3yx.∴(x+3y),当且仅当x=3y时取等.令x+3y=t,(t>0),则6t≤t2,解得:t≥6,即x+3y≥6.故选D.
21.【答案】B
/
22.【答案】D
【解析】函数y=f(x)的图象与y=log2(x+a)的图象关于直线y=–x对称,设f(x)上任意一点为(x,y),则(x,y)关于直线y=–x对称的点为(–y,–x),把(–y,–x)代入y=log2(x+a),得–x=log2(–y+a),∴f(x)=–2–x+a,∵f(–2)+f(–1)=2,∴–22+a–2+a=2,解得a=4.故选D.
23.【答案】B
【解析】由–x2–2x+3>0,解得:–3
【解析】设t=x2–4x–5,由t>0可得x>5或x<–1,则y=t在(0,+∞)递减,由t=x2–4x–5在(5,+∞)递增,可得函数f(x)的减区间为(5,+∞).故选C.
25.【答案】C
【解析】设x>0,–x<0,f(x)为R上的奇函数,且x<0时,f(x)=log2(1–x),则f(–x)=log2(1+x)=–f(x),∴f(x)=–log2(1+x),∴f(1)=–1,∴f(f(1))=f(–1)=log22=1.故选C.
26.【答案】B
【解析】∵实数a,b满足a>b>1,m=loga(logab),,,∴0=loga1
27.【答案】{a|1
【解析】∵f(x)=a?2x+3–a=a(2x–1)+3过定点(0,3),∴f(x),的反函数y=f–1(x)的图象经过定点(3,0).故答案为:(3,0).
29.【答案】(0,1)∪[2,+∞)
/
30.【答案】(1)–7;(2).
【解析】(1)原式=
=log39–9=2–9=–7;
(2)
.
31.【答案】单减区间是(,+∞),单增区间是(–∞,–).
【解析】要使函数有意义,当且仅当u=x2–3>0,
即x>或x<–.
又x∈(,+∞)时,u是x的增函数;
x∈(–∞,–)时,u是x的减函数.
而u>0时,y=logu是减函数,
故函数y=log(x2–3)的单减区间是(,+∞),单增区间是(–∞,–).
32.【答案】(1)(–1,1);(2)f(x)为奇函数.
【解析】(1)要使原函数有意义,需满足,
解得–1
(2)∵f(–x)=lg(1–x)–lg(1+x)=–f(x)
∴f(x)为奇函数.
33.【答案】(1)(–1,1)(2)奇函数,理由详见解析;(3)(0,1).
/
(3)若f()=2,
∴loga(1+)–loga(1–)=loga4=2,
解得a=2,
∴f(x)=log2(1+x)–log2(1–x),
若f(x)>0,则log2(x+1)>log2(1–x),
∴x+1>1–x>0,
解得0
34.【答案】D
【解析】a=log2e>1,0
35.【答案】D
【解析】∵a=log3,c==log35,且5,∴,则b=,∴c>a>b.故选D.
36.【答案】B
/
37.【答案】7
【解析】∵常数a∈R,函数f(x)=1og2(x+a).f(x)的反函数的图象经过点(3,1),∴函数f(x)=1og2(x+a)的图象经过点(1,3),∴log2(1+a)=3,解得a=7.故答案为:7.
38.【答案】
【解析】,
∴,则,故答案为:–2.
