高中数学新人教A版必修4课件:第二章平面向量2.2.2向量减法运算及其几何意义:19张PPT
文档属性
| 名称 | 高中数学新人教A版必修4课件:第二章平面向量2.2.2向量减法运算及其几何意义:19张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 756.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-19 00:00:00 | ||
图片预览




文档简介
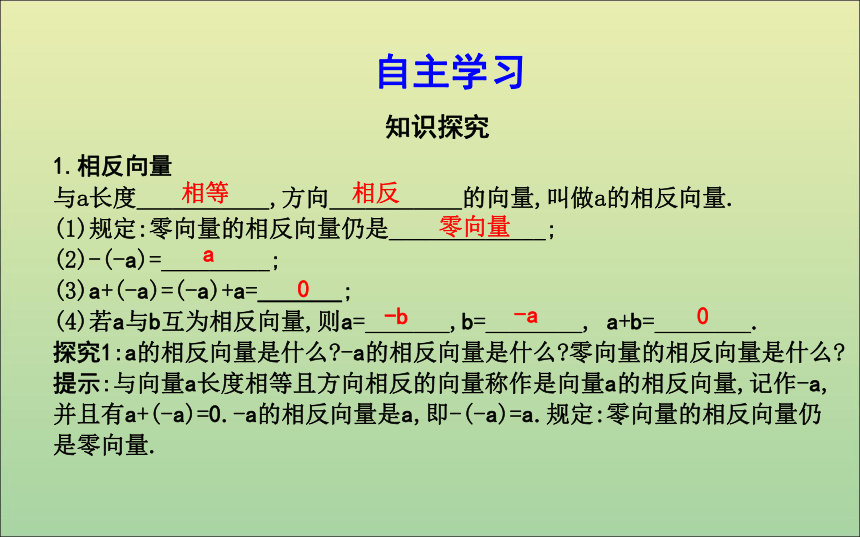
课件19张PPT。2.2.2 向量减法运算及其几何意义课标要求:1.了解相反向量的概念.2.了解差向量的概念和向量加减法间的关系.3.掌握向量减法运算,理解其几何意义.自主学习 1.相反向量
与a长度___________,方向___________的向量,叫做a的相反向量.
(1)规定:零向量的相反向量仍是_____________;
(2)-(-a)=_________;
(3)a+(-a)=(-a)+a=_______;
(4)若a与b互为相反向量,则a=_______,b=________, a+b=________.
探究1:a的相反向量是什么?-a的相反向量是什么?零向量的相反向量是什么?
提示:与向量a长度相等且方向相反的向量称作是向量a的相反向量,记作-a,并且有a+(-a)=0.-a的相反向量是a,即-(-a)=a.规定:零向量的相反向量仍是零向量.知识探究相等零向量a0-b-a0相反(-b) 相反向量2.向量减法
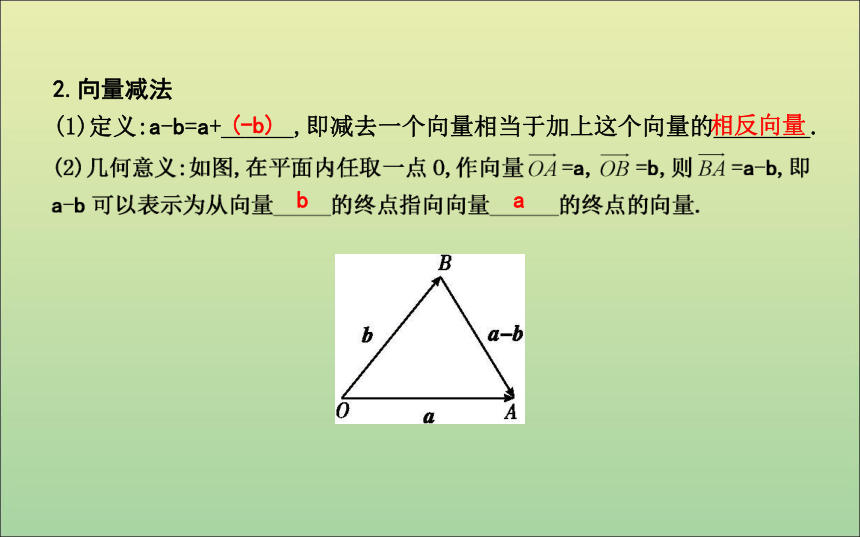
(1)定义:a-b=a+______,即减去一个向量相当于加上这个向量的________. ba探究2:向量减法的三角形法则是什么?
提示:当把两个向量a,b的始点移到同一点时,它们的差向量a-b可以通过下面的作法得到:
①连接两个向量(a与b)的终点;
②差向量a-b的方向是指向被减向量的终点.
这种求差向量a-b的方法叫向量减法的三角形法则.概括为“移为共始点,连接两终点,方向指被减”.【拓展延伸】
非零共线向量a,b的差为a-b,
(1)若a,b反向,则a-b与a同向,且︱a-b︱=︱a︱+︱b︱,其几何意义如图(1)所示;
(2)若a,b同向,①若︱a︱>︱b︱,则a-b与a同向,且︱a-b︱=︱a︱-︱b︱,其几何意义如图(2)所示;
②若︱a︱<︱b︱,则a-b与a反向,且︱a-b︱=︱b︱-︱a︱,其几何意义如图(3)所示;
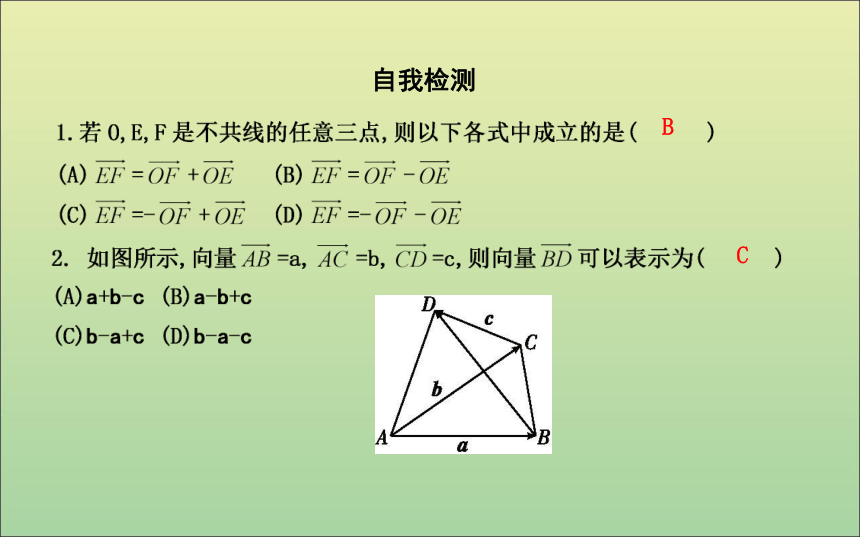
③若︱a︱=︱b︱,则a-b=0,其几何意义如图(4)所示.自我检测BCD答案:2答案:③④题型一 向量的减法运算课堂探究 题后反思 向量减法运算的解题思路:(1)转化为加法运算;(2)直接利用减法运算的几何意义,即三角形法则.(2)如图,已知向量a,b,c不共线,求作向量a+b-c.题型二 用已知向量表示其他向量方法技巧 用已知向量表示其他向量的一般步骤为
(1)观察待表示的向量位置;(2)寻找相应的平行四边形或三角形;(3)运用法则找关系,化简得结果.两个向量差与和的长度题型三 【例3】 已知︱a︱=6,︱b︱=8,且︱a+b︱=︱a-b︱,求︱a-b︱.方法技巧 ︱a+b︱与︱a-b︱的关系:
按向量加法的平行四边形法则、减法的三角形法则得出︱a+b︱与︱a-
b︱是平行四边形的两条对角线是解题关键.即时训练3-1:已知向量a,b满足︱a︱=6,︱b︱=8,︱a-b︱=10,则︱a+b︱=
.?解析: 因为︱a︱=6,︱b︱=8,︱a-b︱=10,
所以︱a︱2+︱b︱2=︱a-b︱2,如图a,b,a-b构成直角三角形.
所以︱a+b︱=︱a-b︱=10.
答案:10
与a长度___________,方向___________的向量,叫做a的相反向量.
(1)规定:零向量的相反向量仍是_____________;
(2)-(-a)=_________;
(3)a+(-a)=(-a)+a=_______;
(4)若a与b互为相反向量,则a=_______,b=________, a+b=________.
探究1:a的相反向量是什么?-a的相反向量是什么?零向量的相反向量是什么?
提示:与向量a长度相等且方向相反的向量称作是向量a的相反向量,记作-a,并且有a+(-a)=0.-a的相反向量是a,即-(-a)=a.规定:零向量的相反向量仍是零向量.知识探究相等零向量a0-b-a0相反(-b) 相反向量2.向量减法
(1)定义:a-b=a+______,即减去一个向量相当于加上这个向量的________. ba探究2:向量减法的三角形法则是什么?
提示:当把两个向量a,b的始点移到同一点时,它们的差向量a-b可以通过下面的作法得到:
①连接两个向量(a与b)的终点;
②差向量a-b的方向是指向被减向量的终点.
这种求差向量a-b的方法叫向量减法的三角形法则.概括为“移为共始点,连接两终点,方向指被减”.【拓展延伸】
非零共线向量a,b的差为a-b,
(1)若a,b反向,则a-b与a同向,且︱a-b︱=︱a︱+︱b︱,其几何意义如图(1)所示;
(2)若a,b同向,①若︱a︱>︱b︱,则a-b与a同向,且︱a-b︱=︱a︱-︱b︱,其几何意义如图(2)所示;
②若︱a︱<︱b︱,则a-b与a反向,且︱a-b︱=︱b︱-︱a︱,其几何意义如图(3)所示;
③若︱a︱=︱b︱,则a-b=0,其几何意义如图(4)所示.自我检测BCD答案:2答案:③④题型一 向量的减法运算课堂探究 题后反思 向量减法运算的解题思路:(1)转化为加法运算;(2)直接利用减法运算的几何意义,即三角形法则.(2)如图,已知向量a,b,c不共线,求作向量a+b-c.题型二 用已知向量表示其他向量方法技巧 用已知向量表示其他向量的一般步骤为
(1)观察待表示的向量位置;(2)寻找相应的平行四边形或三角形;(3)运用法则找关系,化简得结果.两个向量差与和的长度题型三 【例3】 已知︱a︱=6,︱b︱=8,且︱a+b︱=︱a-b︱,求︱a-b︱.方法技巧 ︱a+b︱与︱a-b︱的关系:
按向量加法的平行四边形法则、减法的三角形法则得出︱a+b︱与︱a-
b︱是平行四边形的两条对角线是解题关键.即时训练3-1:已知向量a,b满足︱a︱=6,︱b︱=8,︱a-b︱=10,则︱a+b︱=
.?解析: 因为︱a︱=6,︱b︱=8,︱a-b︱=10,
所以︱a︱2+︱b︱2=︱a-b︱2,如图a,b,a-b构成直角三角形.
所以︱a+b︱=︱a-b︱=10.
答案:10
