高中数学新人教A版必修4课件:第二章平面向量2.3.1平面向量基本定理:24张PPT
文档属性
| 名称 | 高中数学新人教A版必修4课件:第二章平面向量2.3.1平面向量基本定理:24张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 882.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-19 09:46:03 | ||
图片预览








文档简介
课件24张PPT。2.3 平面向量的基本定理及坐标表示
2.3.1 平面向量基本定理课标要求:1.了解平面向量基本定理产生的过程和基底的含义,理解平面向量基本定理.2.理解两个向量夹角的定义,两向量垂直的定义.3.掌握平面向量基本定理并能熟练应用.自主学习 1.平面向量基本定理
(1)定理:如果e1,e2是同一平面内的两个_____________向量,那么对于这一平面内的任意向量a,有且只有一对实数λ1,λ2,使a=________________.
(2)我们把不共线的向量e1,e2叫做表示这一平面内所有向量的一组______.
探究1:如果e1,e2是共线向量,那么向量a能否用e1,e2表示?为什么?
提示:不一定,当a与e1共线时可以表示,否则不能表示.知识探究不共线λ1e1+λ2e2基底2.两向量的夹角
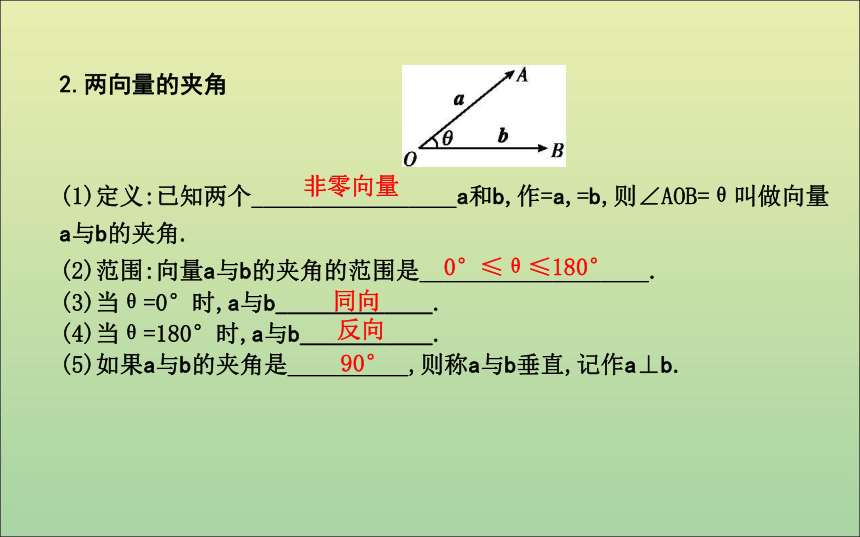
(1)定义:已知两个_________________a和b,作=a,=b,则∠AOB=θ叫做向量a与b的夹角.
(2)范围:向量a与b的夹角的范围是___________________.
(3)当θ=0°时,a与b_____________.
(4)当θ=180°时,a与b___________.
(5)如果a与b的夹角是__________,则称a与b垂直,记作a⊥b.非零向量0°≤θ≤180° 同向反向90° 注意:
如图所示,向量a与b的夹角不是θ,而是180°-θ.
探究2:直线的夹角和向量的夹角有什么区别?
提示:①向量的夹角是针对非零向量定义的【拓展延伸】
对平面向量基本定理的理解
(1)这个定理告诉我们,在平面内任一向量都可以沿两个不共线的方向分解成两个向量的和,且这样的分解是唯一的,同一非零向量在不同的基底下的分解式是不同的,而零向量的分解式是唯一的,即0=λ1e1+λ2e2,且λ1=λ2=0.
(2)由平面向量基本定理可知,如果将平面内向量的起点放在一起,那么平面内的任意一个点都可以通过两个不共线的向量得到表示,也就是说,平面内的点可以由平面内的一个点及两个不共线的向量来表示.
(3)由平面向量的基本定理知,在平面内任取两个不共线的向量作为一组基底,则平面内的任一向量都可以用这组基底表示出来,因而可以简化向量的个数.(4)由向量共线定理可知,任意一个向量都可以用一个与它共线的非零向量线性表示,而且这种表示是唯一的.因此平面向量基本定理是向量共线定理从一维到二维的推广.(6)平面向量基本定理可推广为:在平面内任意三个不共线的向量中,任何一个向量都可表示为其余两个向量的线性组合,且形式唯一.自我检测D2.已知向量a=e1-2e2,b=2e1+e2,其中e1,e2不共线,则a+b与c=6e1-2e2的关系是( )
(A)不共线 (B)共线 (C)相等 (D)不确定B1.设e1,e2是同一平面内的两个向量,则有( )
(A)e1,e2一定共线
(B)同一平面内的任一向量a,都有a=λe1+μe2(λ,μ∈R)
(C)若平面内存在向量a,使得a=λe1+μe2(λ,μ∈R),则e1,e2一定不共线
(D)若平面内的任一向量a,都有a=λe1+μe2(λ,μ∈R),则e1,e2一定不共线D答案:120°5.已知向量a与b是一组基底,实数x,y满足(3x-4y)a+(2x-3y)b=6a+3b,则x-y= .?答案:3题型一 用基底表示向量课堂探究解:(1)易知d≠0,假设存在实数λ,使得c=λd,
则2a-b=λ(3a-2b),即(2-3λ)a+(2λ-1)b=0.
由于a,b不共线,从而2-3λ=2λ-1=0,这样的λ是不存在的,从而假设不成立,即c,d不共线,故c,d能构成一组基底.方法技巧 判断基底的依据
判断两个向量能否构成一组基底,主要看这两个向量是否共线.此外,一个平面的基底一旦确定,那么平面内任意一个向量都可以由这组基底唯一表示.即时训练1-1:(1)e1,e2是平面内所有向量的一组基底,则下列四组向量中不能作为一组基底的是( )
(A)e1和e1+e2 (B)e1-2e2和e2-2e1
(C)e1-2e2和4e2-2e1 (D)e1+e2和e1-e2解析:(1)C中,e1-2e2与4e2-2e1共线,不能作为基底.
故选C.
答案:(1)C题型二 向量的夹角问题【例2】 已知︱a︱=︱b︱=2,且a与b的夹角为60°,则a+b与a的夹角是
,a-b与a的夹角是 ,a+b与a-b的夹角是 .?方法技巧 求两个向量的夹角关键是利用平移的方法使两个向量起点重合,根据向量夹角的概念确定夹角,再依据平面图形的知识求解向量的夹角,过程简记为“一作二证三算”.答案:(1)B (2)已知向量a,b,c满足︱a︱=1,︱b︱=2,c=a+b,c⊥a,则a,b的夹角等于
.?答案:(2)120°平面向量基本定理的应用题型三 即时训练3-1: 如图所示,在△ABC中,点M是BC的中点,点N在边AC上,且AN=
2NC,AM与BN相交于点P,求证:AP∶PM=4∶1.
2.3.1 平面向量基本定理课标要求:1.了解平面向量基本定理产生的过程和基底的含义,理解平面向量基本定理.2.理解两个向量夹角的定义,两向量垂直的定义.3.掌握平面向量基本定理并能熟练应用.自主学习 1.平面向量基本定理
(1)定理:如果e1,e2是同一平面内的两个_____________向量,那么对于这一平面内的任意向量a,有且只有一对实数λ1,λ2,使a=________________.
(2)我们把不共线的向量e1,e2叫做表示这一平面内所有向量的一组______.
探究1:如果e1,e2是共线向量,那么向量a能否用e1,e2表示?为什么?
提示:不一定,当a与e1共线时可以表示,否则不能表示.知识探究不共线λ1e1+λ2e2基底2.两向量的夹角
(1)定义:已知两个_________________a和b,作=a,=b,则∠AOB=θ叫做向量a与b的夹角.
(2)范围:向量a与b的夹角的范围是___________________.
(3)当θ=0°时,a与b_____________.
(4)当θ=180°时,a与b___________.
(5)如果a与b的夹角是__________,则称a与b垂直,记作a⊥b.非零向量0°≤θ≤180° 同向反向90° 注意:
如图所示,向量a与b的夹角不是θ,而是180°-θ.
探究2:直线的夹角和向量的夹角有什么区别?
提示:①向量的夹角是针对非零向量定义的【拓展延伸】
对平面向量基本定理的理解
(1)这个定理告诉我们,在平面内任一向量都可以沿两个不共线的方向分解成两个向量的和,且这样的分解是唯一的,同一非零向量在不同的基底下的分解式是不同的,而零向量的分解式是唯一的,即0=λ1e1+λ2e2,且λ1=λ2=0.
(2)由平面向量基本定理可知,如果将平面内向量的起点放在一起,那么平面内的任意一个点都可以通过两个不共线的向量得到表示,也就是说,平面内的点可以由平面内的一个点及两个不共线的向量来表示.
(3)由平面向量的基本定理知,在平面内任取两个不共线的向量作为一组基底,则平面内的任一向量都可以用这组基底表示出来,因而可以简化向量的个数.(4)由向量共线定理可知,任意一个向量都可以用一个与它共线的非零向量线性表示,而且这种表示是唯一的.因此平面向量基本定理是向量共线定理从一维到二维的推广.(6)平面向量基本定理可推广为:在平面内任意三个不共线的向量中,任何一个向量都可表示为其余两个向量的线性组合,且形式唯一.自我检测D2.已知向量a=e1-2e2,b=2e1+e2,其中e1,e2不共线,则a+b与c=6e1-2e2的关系是( )
(A)不共线 (B)共线 (C)相等 (D)不确定B1.设e1,e2是同一平面内的两个向量,则有( )
(A)e1,e2一定共线
(B)同一平面内的任一向量a,都有a=λe1+μe2(λ,μ∈R)
(C)若平面内存在向量a,使得a=λe1+μe2(λ,μ∈R),则e1,e2一定不共线
(D)若平面内的任一向量a,都有a=λe1+μe2(λ,μ∈R),则e1,e2一定不共线D答案:120°5.已知向量a与b是一组基底,实数x,y满足(3x-4y)a+(2x-3y)b=6a+3b,则x-y= .?答案:3题型一 用基底表示向量课堂探究解:(1)易知d≠0,假设存在实数λ,使得c=λd,
则2a-b=λ(3a-2b),即(2-3λ)a+(2λ-1)b=0.
由于a,b不共线,从而2-3λ=2λ-1=0,这样的λ是不存在的,从而假设不成立,即c,d不共线,故c,d能构成一组基底.方法技巧 判断基底的依据
判断两个向量能否构成一组基底,主要看这两个向量是否共线.此外,一个平面的基底一旦确定,那么平面内任意一个向量都可以由这组基底唯一表示.即时训练1-1:(1)e1,e2是平面内所有向量的一组基底,则下列四组向量中不能作为一组基底的是( )
(A)e1和e1+e2 (B)e1-2e2和e2-2e1
(C)e1-2e2和4e2-2e1 (D)e1+e2和e1-e2解析:(1)C中,e1-2e2与4e2-2e1共线,不能作为基底.
故选C.
答案:(1)C题型二 向量的夹角问题【例2】 已知︱a︱=︱b︱=2,且a与b的夹角为60°,则a+b与a的夹角是
,a-b与a的夹角是 ,a+b与a-b的夹角是 .?方法技巧 求两个向量的夹角关键是利用平移的方法使两个向量起点重合,根据向量夹角的概念确定夹角,再依据平面图形的知识求解向量的夹角,过程简记为“一作二证三算”.答案:(1)B (2)已知向量a,b,c满足︱a︱=1,︱b︱=2,c=a+b,c⊥a,则a,b的夹角等于
.?答案:(2)120°平面向量基本定理的应用题型三 即时训练3-1: 如图所示,在△ABC中,点M是BC的中点,点N在边AC上,且AN=
2NC,AM与BN相交于点P,求证:AP∶PM=4∶1.
