高中数学新人教A版必修4课件:第二章平面向量2.4.1平面向量数量积的物理背景及其含义:26张PPT
文档属性
| 名称 | 高中数学新人教A版必修4课件:第二章平面向量2.4.1平面向量数量积的物理背景及其含义:26张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 915.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-19 09:47:07 | ||
图片预览







文档简介
课件26张PPT。2.4 平面向量的数量积
2.4.1 平面向量数量积的物理背景及其含义课标要求:1.理解平面向量数量积的含义及其物理意义.2.掌握数量积公式,理解其几何意义及投影的定义.3.掌握平面向量数量积的重要性质及运算律,并能运用这些性质和运算律解决有关问题.自主学习 1.向量数量积的定义
(1)已知两个非零向量a与b,它们的夹角为θ,则把数量________________叫做a与b的数量积(或内积),记作a·b,即a·b=________________________.?
(2)规定,零向量与任一向量的数量积均为_______.
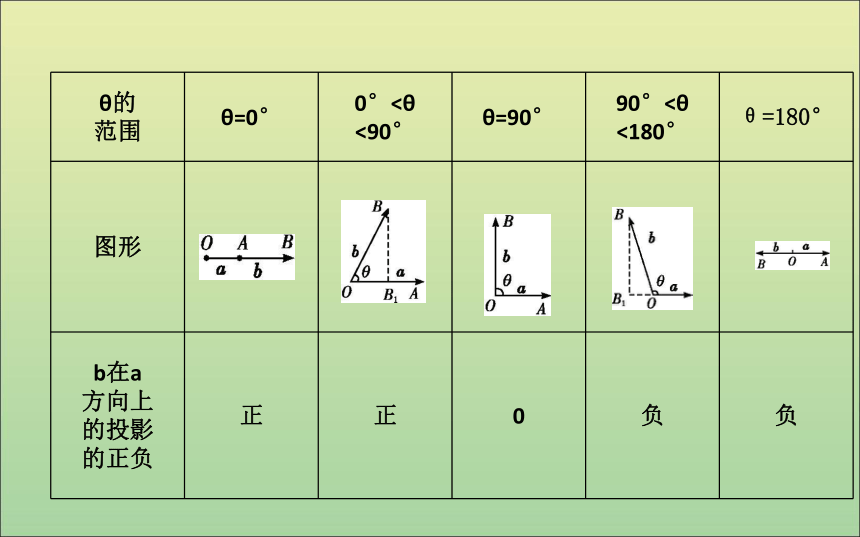
探究1:对于两个非零向量a与b,夹角为θ,其数量积a·b何时为正数?何时为负数?何时为零?
提示:当0°≤θ<90°时,a·b>0;
当90°<θ≤180°时,a·b<0;
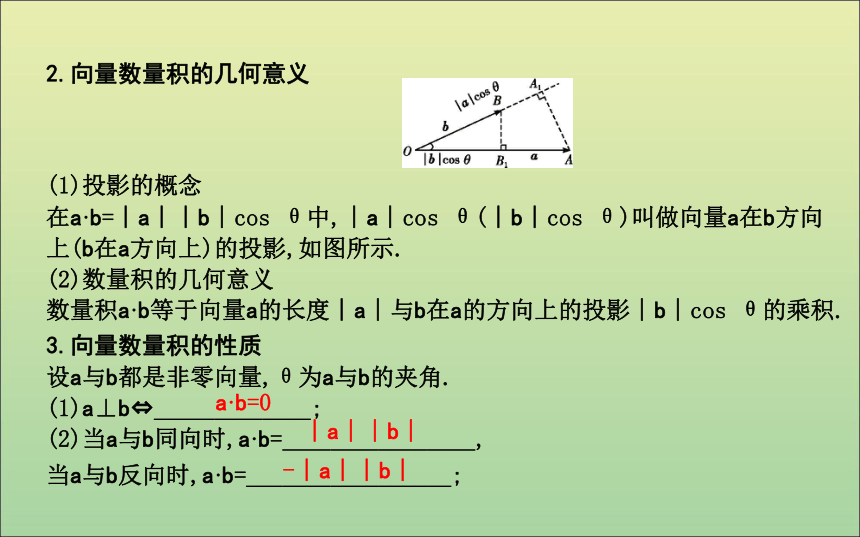
当θ=90°时,a·b=0.知识探究︱a︱︱b︱cos θ︱a︱︱b︱cos θ02.向量数量积的几何意义
(1)投影的概念
在a·b=︱a︱︱b︱cos θ中,︱a︱cos θ(︱b︱cos θ)叫做向量a在b方向上(b在a方向上)的投影,如图所示.
(2)数量积的几何意义
数量积a·b等于向量a的长度︱a︱与b在a的方向上的投影︱b︱cos θ的乘积.
3.向量数量积的性质
设a与b都是非零向量,θ为a与b的夹角.
(1)a⊥b?_____________;
(2)当a与b同向时,a·b=________________,
当a与b反向时,a·b=_________________;a·b=0︱a︱︱b︱-︱a︱︱b︱(5)︱a·b︱_______︱a︱︱b︱.
探究2:两个向量的数量积大于0,夹角一定是锐角吗?两个向量的数量积小于0,两个向量的夹角一定是钝角吗?a2≤4.向量数量积的运算律
已知向量a,b,c和实数λ,则
(1)a·b=__________;
(2)(λa)·b=_____________=a·(λb);
(3)(a+b)·c=a·c+b·c.
注意:a·b=a·cb=c,因为a·b=a·c?a·(b-c)=0?a⊥(b-c),此时不一定有b=c.
【拓展延伸】
对于数量积的进一步理解:
(1)投影是一个数量而不是向量.b·aλ(a·b)(3)由a·b=︱a︱︱b︱cos θ可得,
当θ为锐角时,a·b>0且a·b≠︱a︱︱b︱;
当θ为钝角时,a·b<0且a·b≠-︱a︱︱b︱;
当θ=0°时,a·b=︱a︱︱b︱;
当θ=180°时,a·b=-︱a︱︱b︱;
当θ=90°时,a·b=0.自我检测BD题型一 数量积的基本运算课堂探究【例1】 已知︱a︱=4,︱b︱=5,当(1)a∥b;(2)a⊥b;(3)a与b的夹角为30°时,分别求a与b的数量积.解:(1)a∥b,若a与b同向,则a与b的夹角θ=0°,a·b=︱a︱·︱b︱·cos 0°=
4×5=20;若a与b反向,则θ=180°,所以a·b=︱a︱·︱b︱cos 180°=4×
5×(-1)=-20.
(2)当a⊥b时,θ=90°,所以a·b=︱a︱·︱b︱cos 90°=0.变式探究:把(3)中的a与b的夹角改为120°,试求(2a-b)·(3a+2b).方法技巧 求平面向量数量积的步骤
(1)求a与b的夹角θ,θ∈[0,π];
(2)分别求︱a︱和︱b︱;
(3)求数量积,即a·b=︱a︱︱b︱cos θ,要特别注意书写时a与b之间用实心圆点“·”连接,而不能用“×”连接,也不能省去.(2)若向量a+b+c=0,且︱a︱=3,︱b︱=1,︱c︱=4,求a·b+b·c+c·a的值.题型二 求向量的模【例2】 (1)已知向量a,b满足a·b=0,︱a︱=1,︱b︱=1,则︱a-3b︱= .?方法技巧 (1)要求几个向量线性运算后的模,可先求其平方,利用数量积的计算易解.
(2)已知两个向量线性运算后的模求某个向量的模,可把条件平方后化为所求目标的方程求解.答案:(1)A答案:(2)2两向量的垂直与夹角题型三 【例3】 (1)若︱a︱=1,︱b︱=2,c=a+b且c⊥a,则向量a与b的夹角为( )
(A)30° (B)60° (C)120° (D)150°答案:(1)C(2)若非零向量a,b满足︱a︱=3︱b︱=︱a+2b︱,则a与b夹角的余弦值为
.?方法技巧 向量的垂直与夹角的范围
(1)已知非零向量a,b,若a⊥b,则a·b=0,反之也成立.答案:1(2)已知单位向量e1,e2的夹角为60°,求向量a=e1+e2,b=e2-2e1的夹角.
2.4.1 平面向量数量积的物理背景及其含义课标要求:1.理解平面向量数量积的含义及其物理意义.2.掌握数量积公式,理解其几何意义及投影的定义.3.掌握平面向量数量积的重要性质及运算律,并能运用这些性质和运算律解决有关问题.自主学习 1.向量数量积的定义
(1)已知两个非零向量a与b,它们的夹角为θ,则把数量________________叫做a与b的数量积(或内积),记作a·b,即a·b=________________________.?
(2)规定,零向量与任一向量的数量积均为_______.
探究1:对于两个非零向量a与b,夹角为θ,其数量积a·b何时为正数?何时为负数?何时为零?
提示:当0°≤θ<90°时,a·b>0;
当90°<θ≤180°时,a·b<0;
当θ=90°时,a·b=0.知识探究︱a︱︱b︱cos θ︱a︱︱b︱cos θ02.向量数量积的几何意义
(1)投影的概念
在a·b=︱a︱︱b︱cos θ中,︱a︱cos θ(︱b︱cos θ)叫做向量a在b方向上(b在a方向上)的投影,如图所示.
(2)数量积的几何意义
数量积a·b等于向量a的长度︱a︱与b在a的方向上的投影︱b︱cos θ的乘积.
3.向量数量积的性质
设a与b都是非零向量,θ为a与b的夹角.
(1)a⊥b?_____________;
(2)当a与b同向时,a·b=________________,
当a与b反向时,a·b=_________________;a·b=0︱a︱︱b︱-︱a︱︱b︱(5)︱a·b︱_______︱a︱︱b︱.
探究2:两个向量的数量积大于0,夹角一定是锐角吗?两个向量的数量积小于0,两个向量的夹角一定是钝角吗?a2≤4.向量数量积的运算律
已知向量a,b,c和实数λ,则
(1)a·b=__________;
(2)(λa)·b=_____________=a·(λb);
(3)(a+b)·c=a·c+b·c.
注意:a·b=a·cb=c,因为a·b=a·c?a·(b-c)=0?a⊥(b-c),此时不一定有b=c.
【拓展延伸】
对于数量积的进一步理解:
(1)投影是一个数量而不是向量.b·aλ(a·b)(3)由a·b=︱a︱︱b︱cos θ可得,
当θ为锐角时,a·b>0且a·b≠︱a︱︱b︱;
当θ为钝角时,a·b<0且a·b≠-︱a︱︱b︱;
当θ=0°时,a·b=︱a︱︱b︱;
当θ=180°时,a·b=-︱a︱︱b︱;
当θ=90°时,a·b=0.自我检测BD题型一 数量积的基本运算课堂探究【例1】 已知︱a︱=4,︱b︱=5,当(1)a∥b;(2)a⊥b;(3)a与b的夹角为30°时,分别求a与b的数量积.解:(1)a∥b,若a与b同向,则a与b的夹角θ=0°,a·b=︱a︱·︱b︱·cos 0°=
4×5=20;若a与b反向,则θ=180°,所以a·b=︱a︱·︱b︱cos 180°=4×
5×(-1)=-20.
(2)当a⊥b时,θ=90°,所以a·b=︱a︱·︱b︱cos 90°=0.变式探究:把(3)中的a与b的夹角改为120°,试求(2a-b)·(3a+2b).方法技巧 求平面向量数量积的步骤
(1)求a与b的夹角θ,θ∈[0,π];
(2)分别求︱a︱和︱b︱;
(3)求数量积,即a·b=︱a︱︱b︱cos θ,要特别注意书写时a与b之间用实心圆点“·”连接,而不能用“×”连接,也不能省去.(2)若向量a+b+c=0,且︱a︱=3,︱b︱=1,︱c︱=4,求a·b+b·c+c·a的值.题型二 求向量的模【例2】 (1)已知向量a,b满足a·b=0,︱a︱=1,︱b︱=1,则︱a-3b︱= .?方法技巧 (1)要求几个向量线性运算后的模,可先求其平方,利用数量积的计算易解.
(2)已知两个向量线性运算后的模求某个向量的模,可把条件平方后化为所求目标的方程求解.答案:(1)A答案:(2)2两向量的垂直与夹角题型三 【例3】 (1)若︱a︱=1,︱b︱=2,c=a+b且c⊥a,则向量a与b的夹角为( )
(A)30° (B)60° (C)120° (D)150°答案:(1)C(2)若非零向量a,b满足︱a︱=3︱b︱=︱a+2b︱,则a与b夹角的余弦值为
.?方法技巧 向量的垂直与夹角的范围
(1)已知非零向量a,b,若a⊥b,则a·b=0,反之也成立.答案:1(2)已知单位向量e1,e2的夹角为60°,求向量a=e1+e2,b=e2-2e1的夹角.
