高中数学新人教A版必修4课件:第三章三角恒等变换3.1.2两角和与差的正弦、余弦、正切公式:31张PPT
文档属性
| 名称 | 高中数学新人教A版必修4课件:第三章三角恒等变换3.1.2两角和与差的正弦、余弦、正切公式:31张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-19 09:50:16 | ||
图片预览





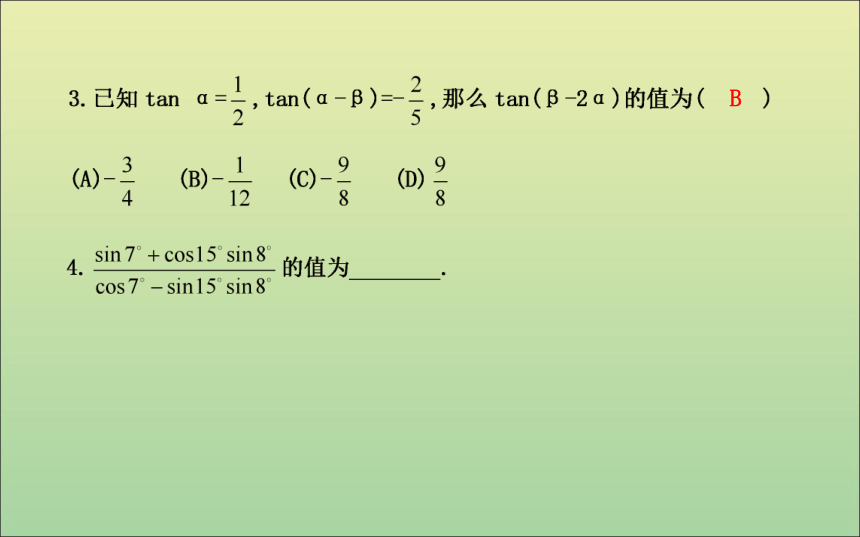




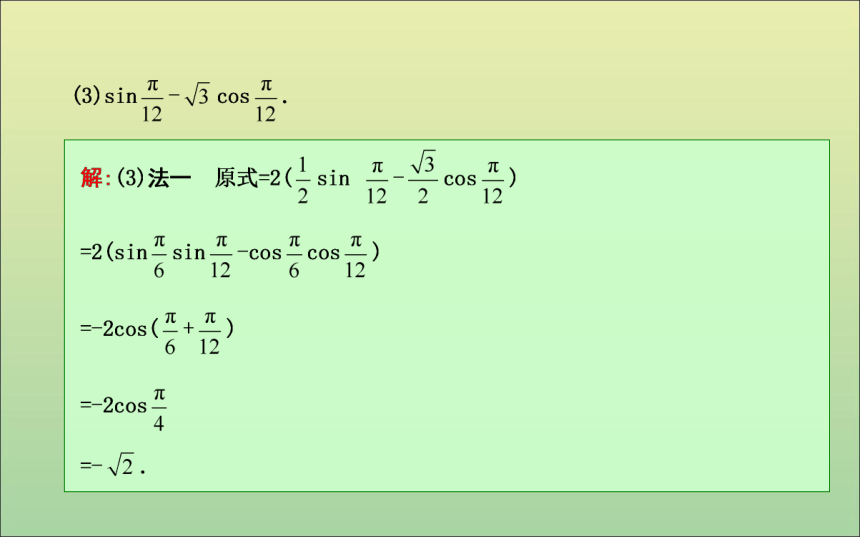
文档简介
课件31张PPT。3.1.2 两角和与差的正弦、余弦、正切公式课标要求:1.能根据两角差的余弦公式推导出两角和与差的正弦、正切公式和两角和的余弦公式.2.熟练掌握两角和与差的正弦、余弦、正切公式的特征.3.能灵活运用公式进行化简和求值.自主学习 1.两角和的余弦公式
cos(α+β)= ,简记为C(α+β).?
2.两角和与差的正弦公式
S(α+β):sin(α+β)= ;?
S(α-β):sin(α-β)= .?
3.两角和与差的正切公式
T(α+β):tan(α+β)= ;
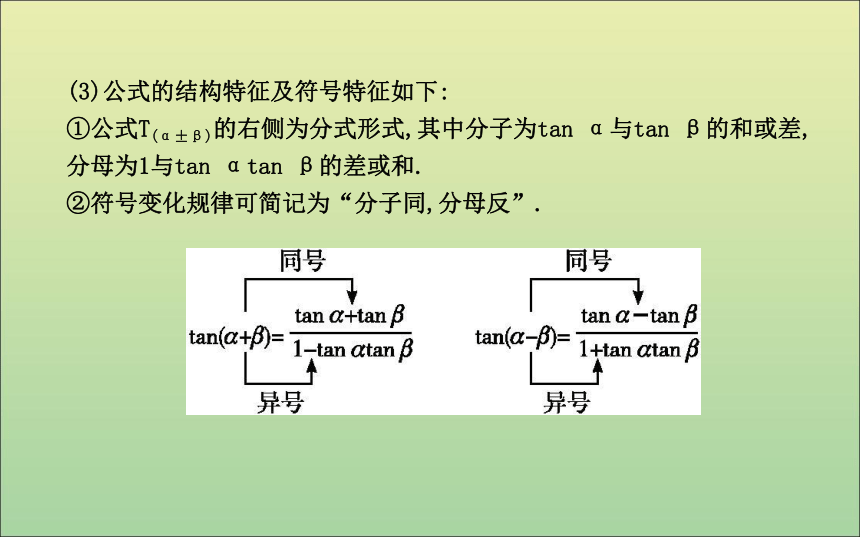
T(α-β):tan(α-β)= .知识探究cos αcos β-sin αsin βsin αcos β+cos αsin βsin αcos β-cos αsin β(3)公式的结构特征及符号特征如下:
①公式T(α±β)的右侧为分式形式,其中分子为tan α与tan β的和或差,分母为1与tan αtan β的差或和.
②符号变化规律可简记为“分子同,分母反”.自我检测A1.cos(x+2y)+2sin(x+y)sin y可化简为( )
(A)cos x (B)sin x
(C)cos(x+y) (D)cos(x-y)AB解析:b=2cos 65°,
c=2(cos 43°cos 24°-sin 24°sin 43°)
=2cos 67°,所以b>a>c.
答案:b>a>c题型一 两角和与差的正弦、余弦课堂探究【例1】 (1)cos 105°;(2)sin 14°cos 16°+sin 76°cos 74°;误区警示 在利用诱导公式与和差角的正、余弦公式时一定要熟记公式并能灵活应用,特别是符号一定要准确,否则易出错.题型二 和差角的正切公式(2)tan 20°·tan 30°+tan 30°·tan 40°+tan 40°·tan 20°.方法技巧(2)若化简的式子中出现了“tan α±tan β”及“tan α·tan β”两个整体,常考虑tan(α±β)的变形公式.即时训练2-1:tan 22°+tan 23°+tan 22°tan 23° = .?答案:1题型三 三角函数的条件求值题后反思 (1)解决三角函数条件求值问题的关键是寻找已知角与所求角之间的关系,恰当地拆角、凑角,合理地选用公式.
(2)常见角的变换有α=(α+β)-β,α=β-(β-α),2α=(α+β)+(α- β)等.(3)求2α-β的值.题型四 辅助角公式的应用答案:(1)2 -1答案:(2)π方法技巧
cos(α+β)= ,简记为C(α+β).?
2.两角和与差的正弦公式
S(α+β):sin(α+β)= ;?
S(α-β):sin(α-β)= .?
3.两角和与差的正切公式
T(α+β):tan(α+β)= ;
T(α-β):tan(α-β)= .知识探究cos αcos β-sin αsin βsin αcos β+cos αsin βsin αcos β-cos αsin β(3)公式的结构特征及符号特征如下:
①公式T(α±β)的右侧为分式形式,其中分子为tan α与tan β的和或差,分母为1与tan αtan β的差或和.
②符号变化规律可简记为“分子同,分母反”.自我检测A1.cos(x+2y)+2sin(x+y)sin y可化简为( )
(A)cos x (B)sin x
(C)cos(x+y) (D)cos(x-y)AB解析:b=2cos 65°,
c=2(cos 43°cos 24°-sin 24°sin 43°)
=2cos 67°,所以b>a>c.
答案:b>a>c题型一 两角和与差的正弦、余弦课堂探究【例1】 (1)cos 105°;(2)sin 14°cos 16°+sin 76°cos 74°;误区警示 在利用诱导公式与和差角的正、余弦公式时一定要熟记公式并能灵活应用,特别是符号一定要准确,否则易出错.题型二 和差角的正切公式(2)tan 20°·tan 30°+tan 30°·tan 40°+tan 40°·tan 20°.方法技巧(2)若化简的式子中出现了“tan α±tan β”及“tan α·tan β”两个整体,常考虑tan(α±β)的变形公式.即时训练2-1:tan 22°+tan 23°+tan 22°tan 23° = .?答案:1题型三 三角函数的条件求值题后反思 (1)解决三角函数条件求值问题的关键是寻找已知角与所求角之间的关系,恰当地拆角、凑角,合理地选用公式.
(2)常见角的变换有α=(α+β)-β,α=β-(β-α),2α=(α+β)+(α- β)等.(3)求2α-β的值.题型四 辅助角公式的应用答案:(1)2 -1答案:(2)π方法技巧
