北师大版初中数学七年级上册第五章一元一次方程全章复习与巩固(提高)学案含解析
文档属性
| 名称 | 北师大版初中数学七年级上册第五章一元一次方程全章复习与巩固(提高)学案含解析 | 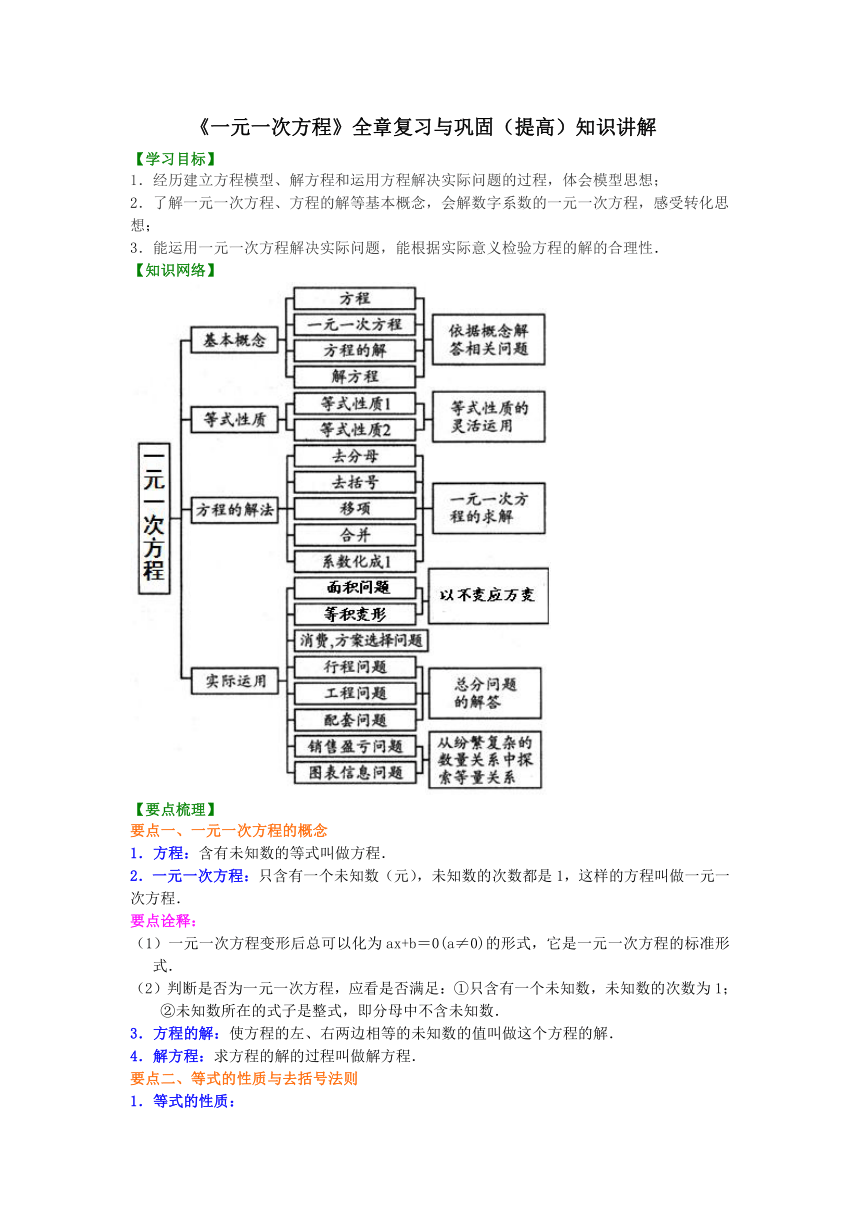 | |
| 格式 | zip | ||
| 文件大小 | 237.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-19 09:11:36 | ||
图片预览





文档简介
《一元一次方程》全章复习与巩固(提高)知识讲解
【学习目标】
1.经历建立方程模型、解方程和运用方程解决实际问题的过程,体会模型思想;
2.了解一元一次方程、方程的解等基本概念,会解数字系数的一元一次方程,感受转化思想;
3.能运用一元一次方程解决实际问题,能根据实际意义检验方程的解的合理性.
【知识网络】
【要点梳理】
要点一、一元一次方程的概念
1.方程:含有未知数的等式叫做方程.
2.一元一次方程:只含有一个未知数(元),未知数的次数都是1,这样的方程叫做一元一次方程.
要点诠释:
(1)一元一次方程变形后总可以化为ax+b=0(a≠0)的形式,它是一元一次方程的标准形式.
(2)判断是否为一元一次方程,应看是否满足:①只含有一个未知数,未知数的次数为1;
②未知数所在的式子是整式,即分母中不含未知数.
3.方程的解:使方程的左、右两边相等的未知数的值叫做这个方程的解.
4.解方程:求方程的解的过程叫做解方程.
要点二、等式的性质与去括号法则
1.等式的性质:
等式的性质1:等式两边同时加上(或减去)同一个代数式,所得结果仍是等式.
等式的性质2:等式两边乘同一个数,(或除以同一个不为0的数),所得结果仍是等式.
2.合并法则:合并时,把系数相加(减)作为结果的系数,字母和字母的指数保持不变.
3.去括号法则:
(1)括号外的因数是正数,去括号后各项的符号与原括号内相应各项的符号相同.
(2)括号外的因数是负数,去括号后各项的符号与原括号内相应各项的符号相反.
要点三、一元一次方程的解法
解一元一次方程的一般步骤:
(1)去分母:在方程两边同乘以各分母的最小公倍数.
(2)去括号:依据乘法分配律和去括号法则,先去小括号,再去中括号,最后去大括号.
(3)移项:把含有未知数的项移到方程一边,常数项移到方程另一边.
(4)合并:逆用乘法分配律,分别合并含有未知数的项及常数项,把方程化为ax=b(a≠0)的形式.
(5)系数化为1:方程两边同除以未知数的系数得到方程的解(a≠0).
(6)检验:把方程的解代入原方程,若方程左右两边的值相等,则是方程的解;若方程左右两边的值不相等,则不是方程的解.
要点四、用一元一次方程解决实际问题的常见类型
1.等积变形:①形状面积变了,周长没变;②原体积=变化后体积.
2.利润问题:商品利润=商品售价-商品进价
3.行程问题:路程=速度×时间
4.和差倍分问题:增长量=原有量×增长率
5.工程问题:工作量=工作效率×工作时间,各部分劳动量之和=总量
6.银行存贷款问题:本息和=本金+利息,利息=本金×利率×期数
7.数字问题:多位数的表示方法:例如:.
8.方案问题:(1)运用一元一次方程解应用题的方法求解两种方案值相等的情况.
(2)用特殊值试探法选择方案,取小于(或大于)一元一次方程解的值,比较两种方案的优劣性后下结论.
【典型例题】
类型一、一元一次方程的相关概念
1.已知方程(3m-4)x2-(5-3m)x-4m=-2m是关于x的一元一次方程,求m和x的值.
【思路点拨】若一个整式方程经过化简变形后,只含有一个未知数,并且未知数的次数都是1,系数不为0,则这个方程是一元一次方程.
【答案与解析】
解:因为方程(3m-4)x2-(5-3m)x-4m=-2m是关于x的一元一次方程,
所以3m-4=0且5-3m≠0.
由3m-4=0解得,又能使5-3m≠0,所以m的值是.
将代入原方程,则原方程变为,解得.
所以,.
【总结升华】解答这类问题,一定要严格按照一元一次方程的定义.方程(3m-4)x2-(5-3m)x-4m=-2m2是关于x的一元一次方程,就是说x的二次项系数3m-4=0,而x的一次项系数5-3m≠0,m的值必须同时符合这两个条件.
举一反三:
【变式】下面方程变形中,错在哪里:
(1)方程2x=2y两边都减去x+y,得2x-(x+y)=2y-(x+y), 即x-y=-(x-y).
方程 x-y=-(x-y)两边都除以x-y, 得1=-1.
(2),去分母,得3(3-7x)=2(2x+1)+2x,去括号得:9-21x=4x+2+2x.
【答案】(1)答:错在第二步,方程两边不能除以x-y,只有一种可能就是x-y为0了,所以出现了1=-1的错误,也就是说对于等式性质来说,如果想要除以式子来说,这个式子一定是不能为0的.
(2)答:错在第一步,去分母时2x项没乘以公分母6.
2. (2015秋?营山县校级期中)对于ax+b=0(a,b为常数),表述正确的是( )
A.当a≠0时,方程的解是x= B.当a=0,b≠0时,方程有无数解
C.当a=0,b=0,方程无解 D.以上都不正确
【答案】D.
【解析】
解:A、当a≠0时,方程的解是x=﹣,故错误;
B、当a=0,b≠0时,方程无解,故错误;
C、当a=0,b=0,方程有无数解,故错误;
D、以上都不正确.
【总结升华】此题很简单,解答此题的关键是:正确记忆一元一次方程的一般形式中,一次项系数不等于0.
举一反三:
【变式】已知|x+1|+(y+2x)2=0,则________.
【答案】1
类型二、一元一次方程的解法
3.解方程:解方程3{2x-1-[3(2x-1)+3]}=5.
【答案与解析】
解:把2x-1看做一个整体.去括号,得:
3(2x-1)-9(2x-1)-9=5.
合并同类项,得-6(2x-1)=14.
系数化为1得: ,
解得 .
【总结升华】把题目中的2x-1看作一个整体,从而简化了计算过程.本题也可以考虑换元法:设2x-1=a,则原方程化为3[a-(3a+3)]=5.
举一反三:
【变式】解方程
【答案】
解:把方程两边含有分母的项化整为零,得
.
移项,合并同类项得:,
系数化为1得: z=1.
类型三、特殊的一元一次方程的解法
1.解含字母系数的方程
4.解关于的方程:
【思路点拨】这个方程化为标准形式后,未知数x的系数和常数都是以字母形式出现的,所以方程的解的情况与x的系数和常数的取值都有关系.
【答案与解析】
解:原方程可化为:
当时,原方程有唯一解:;
当时,原方程无数个解;
当时,原方程无解;
【总结升华】解含字母系数的方程时,一般化为最简形式,再分类讨论进行求解,注意最后的解不能合并,只能分情况说明.
2.解含绝对值的方程
5. 解方程|x-2|=3.
【答案与解析】
解:当x-2≥0时,原方程可化为x-2=3,得x=5.
当x-2<0时,原方程可化为-(x-2)=3,得 x=-1.
所以x=5和x=-1都是方程|x-2|=3的解.
【总结升华】如图所示,可以看出点-1与5到点2的距离均为3,所以|x-2|=3的意义为在数轴上到点2的距离等于3的点对应的数,即方程|x-2|=3的解为x=-1和x=5.
举一反三:
【变式】若关于的方程无解,只有一个解,有两个解,
则的大小关系为: ( )
A. B. C. D.
【答案】A
类型四、一元一次方程的应用
6.李伟从家里骑摩托车到火车站,如果每小时行30千米,那么比火车开车时间早到15分钟;若每小时行18千米,则比火车开车时间迟到15分钟,现在李伟打算在火车开车前10分钟到达火车站,求李伟此时骑摩托车的速度应是多少?
【思路点拨】本题中的两个不变量为:火车开出的时间和李伟从家到火车站的路程不变.
【答案与解析】
解:设李伟从家到火车站的路程为y千米,则有:
,解得:
由此得到李伟从家出发到火车站正点开车的时间为(小时).
李伟打算在火车开车前10分钟到达火车站时,设李伟骑摩托车的速度为x千米/时, 则有:
(千米/时)
答:李伟此时骑摩托车的速度应是27千米/时.
【总结升华】在解决问题时,当发现某种方法不能解决问题时,应该及时变换思维角度,如本题直接设未知数较难时,应迅速变换思维的角度,合理地设置间接未知数以寻求新的解决问题的途径和方法.
7. 黄冈某地“杜鹃节”期间,某公司70名职工组团前往参观欣赏,旅游景点规定:①门票每人60元,无优惠;②上山游玩可坐景点观光车,观光车有四座和十一座车,四座车每辆60元,十一座车每人10元.公司职工正好坐满每辆车且总费用刚好为4920元时,问公司租用的四座车和十一座车各多少辆?
【答案与解析】
解:设四座车租x辆,十一座车租辆,依题意得:
解得:x=1,
答:公司租用的四座车和十一座车分别是1辆和6辆.
【总结升华】解答本题需从“公司职工正好坐满每辆车且总费用刚好为4920元”中挖掘两个等量关系构建方程求解.
8.某牛奶加工厂有鲜奶9吨,若在市场上直接销售鲜奶,每吨可获取利润500元,制成酸奶销售,每吨可获取利润1200元;制成奶片销售,每吨可获利润2000元,该工厂的生产能力是:如制成酸奶,每天可加工3吨;制成奶片每天可加工1吨,受人员限制,两种加工方式不可同时进行,受气温条件限制,这批牛奶必须在4天内全部销售或加工完毕.为此,该厂某领导提出了两种可行方案:
方案1:尽可能多的制成奶片,其余直接销售鲜牛奶;
方案2:将一部分制成奶片,其余制成酸奶销售,并恰好4天完成.
你认为选择哪种方案获利最多,为什么?
【答案与解析】
解:(1)若选择方案1,依题意,
总利润=2000元×4+500元×(9-4)=10500(元).
(2)若选择方案2.
方法一:
解:设将x吨鲜奶制成奶片,则用(9-x)吨鲜奶制成酸奶销售.
依题意得,,
解得.
当时,.
总利润=2000×1.5+1200×7.5=12000(元).
∵ 12000>10500,
∴ 选择方案2较好.
方法二:
解:设x天生产奶片,则(4-x)天生产酸奶.
x+3(4-x)=9
x=1.5
4-x=2.5
1.5×1×2000+2.5×3×1200=12000(元)
∵ 12000>10500,
∴ 选择方案2较好.
答:选择方案2获利最多,只要在四天内用7.5吨鲜奶加工成酸奶,用1.5吨的鲜奶加工成奶片.
【总结升华】如果题目中的数量关系较复杂,常借助列表,画线段图,示意图等手段帮助我们理顺题目中的数量关系,列出方程.例如本题方案2中的方法一,设将x吨鲜奶制成奶片,则列表如下:
每吨利润
吨数
工效
天数
酸奶
1200
3
奶片
2000
1
合计
9
4
该表可以使条件之间的关系一目了然,从而得到等量关系,当然此题也可以设天数来计算,同学们可根据理解自己选择.
举一反三:
【变式】(2015?吴江市一模)现有甲、乙两种金属的合金10kg,如果加入甲种金属若干,那么重新熔炼后的合金中乙种金属占2份,甲种金属占3份,如果加入的甲种金属是第一次加入的2倍,那么重新熔炼后的合金中乙种金属占3份,甲种金属占7份,第一次加入的甲种金属多少?原来这块合金中甲种金属的百分比是多少?
【答案】
解:设原来这块合金中甲种金属的百分比是x,则甲种金属有10xkg,乙种金属有(10﹣10x)kg,根据题意得
(10﹣10x)÷﹣10=2×[(10﹣10x)÷﹣10],
解得x=40%.
则(10﹣10×40%)÷﹣10=5(kg).
答:第一次加入的甲种金属是5kg,原来这块合金中甲种金属的百分比是40%.
【巩固练习】
一、选择题
1.已知方程是关于x的一元一次方程,则m的值是( ).
A.±1 B.1 C.-1 D.0或1
2.已知是方程的解,那么关于y的方程的解是( ).
A.y=1 B.y=-1 C.y=0 D.方程无解
3.已知,则等于( ).
A. B. C. D.
4.一列火车长100米,以每秒20米的速度通过800米长的隧道,从火车进入隧道起,至火车完全通过所用的时间为( ).
A.50秒 B.40秒 C.45秒 D.55秒
5.一架飞机在两城间飞行,顺风要5.5小时,逆风要6小时,风速为24千米/时,求两城距离x的方程是( ).
A. B.
C. D.
6.(2015?永州)永州市双牌县的阳明山风光秀丽,历史文化源远流长,尤以山顶数万亩野生杜鹃花最为壮观,被誉为“天下第一杜鹃红”.今年“五一”期间举办了“阳明山杜鹃花旅游文化节”,吸引了众多游客前去观光赏花.在文化节开幕式当天,从早晨8:00开始每小时进入阳明山景区的游客人数约为1000人,同时每小时走出景区的游客人数约为600人,已知阳明上景区游客的饱和人数约为2000人,则据此可知开幕式当天该景区游客人数饱和的时间约为( )
A.10:00 B.12:00 C.13:00 D.16:00
7.某书中一道方程题:,□处在印刷时被墨盖住了,查书后面的答案,得知这个方程的解是x=﹣2.5,那么□处应该是数字( ).
A.-2.5 B.2.5 C.5 D.7
8. 已知:,,,,…,
若符合前面式子的规律,则a+b的值为( ).
A. 179 B. 140 C. 109 D. 210
二、填空题
9.已知方程是关于x的一元一次方程,则这个方程的解为________.
10.已知和互为相反数,则________.
11.(2015?温州校级自主招生)对于实数a,b,c,d,规定一种数的运算:=ad﹣bc,那么当=10时,x= .
12.一商店把某商品按标价的九折出售仍可获得20%的利润率,若该商品的进价是每件30元,则标价是每件 元.
13.某种中草药含甲、乙、丙、丁四种草药成分,这四种草药成分的质量比是0.7∶1∶2∶
4.7.现在要配制这种中药1400克,这四种草药分别需要多少克?设每份为克,根据题意,得 .
14.有一列数,按一定的规律排列:―1,2,―4,8,―16,32,―64,128,…,其中某三个相邻数之和为384,这三个数分别是 .
15.已知关于的方程和方程有相同的解,则该方程的解为 .
16. x表示一个两位数, y表示一个三位数, 若把x放在y的左边组成一个五位数记作M1, 把y放在x的左边组成一个五位数记作M2, 则 M1 ( M2 是 的倍数.
三、解答题
17.解方程:
(1).
(2) .
(3)|3x-2|-4=0 .
18.探究:当b为何值时,方程|x-2|=b+1 ① 无解;②只有一个解;③ 有两个解.
19.(2015?海淀区二模)小明坚持长跑健身.他从家匀速跑步到学校,通常需30分钟.某周日,小明与同学相约早上八点学校见,他七点半从家跑步出发,平均每分钟比平时快了40米,结果七点五十五分就到达了学校,求小明家到学校的距离.
20.商场计划拨款9万元,从厂家购进50台电视机,已知该厂家生产三种不同型号的电视机,出场价分别为甲种每台1500元,乙种每台2100元,丙种每台2500元.
(1)若商场同时购进其中两种不同型号的电视机共50台,用去9万元,请你研究一下商场的进货方案;(2)若商场销售一台甲种电视机可获利150元,销售一台乙种电视机可获利200元,销售一台丙种电视机可获利250元.在同时购进两种不同型号的电视机的方案中,为使销售时获利最多,该选择哪种进货方案?
【答案与解析】
一、选择题
1. 【答案】B
【解析】由题意得|m|=1,且m+1≠0,所以m=1,故选B.
2. 【答案】C
【解析】由x=1是方程的解,可代入求出a的值,然后把a的值代入方程a(y+4)=2ay+4a中,求出y的值.
3. 【答案】D
【解析】由原式可得:,将“”看作整体,合并化简即可.
4.【答案】C
【解析】相等关系是:火车所走的路程=火车长度+隧道长度.设火车完全通过所用时间为x秒,可得方程20x=100+800,解得x=45.
5. 【答案】A
【解析】解:∵两城距离为x,顺风要5.5小时,逆风要6小时,
∴顺风速度=,逆风速度=,
∵风速为24千米/时,
∴可列方程为:
6.【答案】C.
【解析】设开幕式当天该景区游客人数饱和的时间约为x点,则
(x﹣8)×(1000﹣600)=2000,解得x=13.
即开幕式当天该景区游客人数饱和的时间约为13:00.
7.【答案】C
【解析】把x=-2.5代入方程,再把□当作未知数解方程即可.
8.【答案】C
【解析】观察规律可得b=10,a=b2-1=99,所以a+b=109.
二、填空题
9.【答案】x=1
【解析】首先将原方程整理成的形式,由一元一次方程的定义可知,二次项系数为0,所以a=5,代入方程中即可求出x的值.
10.【答案】-8
【解析】两数互为相反数,则和为0,由非负数的性质可知m-n+4=0,且n-3=0.从而得m=-1,n=3.
11.【答案】﹣1.
【解析】由题意得,2x+12=10,解得x=﹣1.故答案为:﹣1.
12.【答案】40
【解析】解:设标价为元,则有,解得:
13.【答案】
14.【答案】128,-256,512
【解析】通过观察可得:第个数为:,所以第9,10个数分别为:,经检验满足题意.
15.【答案】
【解析】分别解得这两个关于x的方程的解为,,由它们相等得,代入其中一解可得答案.
16.【答案】9
【解析】M1=1000x+y,M2=100y+x,M1 ( M2=9(111x-11y),所以一定是9的倍数.
三、解答题
17.【解析】
解:(1)整理,得,
去分母,得,
去括号,得,
移项,得,
合并,得,
系数化为1,得.
(2)原方程可化为:
解得:x=
(3)原式可化为:|3x-2|=4
由,可得:;由,可得:
所以原方程的解为:x=2,x=-.
18. 【解析】
解:①当,即 b<-1时,原方程无解;
②当,即 b=-1时,原方程只有一个解;
③ 当,即b>-1时,原方程有两个解.
19.【解析】
解:设小明家到学校的距离为x米,
由题意,得+40=,
解得x=6000.
答:小明家到学校的距离为6000米.
20.【解析】
解:(1)①解:设购进甲种电视机台,则购进乙种电视机(50-)台,根据题意,得
1500+2100(50-)=90000.
解得: =25,则50-=25.
故第一种进货方案是购甲、乙两种型号的电视机各25台.
②设购进甲种电视机台,则购进丙种电视机(50- )台,根据题意,得
1500+2500(50-)=90000.
解得: =35,则50-=15.
故第二种进货方案是购进甲种电视机35台,丙种电视机15台.
③设购进乙种电视机台,则购进丙种电视机(50-)台,购进题意,得
2100+2500(50-)=90000.
解得: =87.5(不合题意).
故此种方案不可行.
(2)上述的第一种方案可获利:150×25+200×25=8750元,
第二种方案可获利:150×35+250×15=9000元,
因为8750<9000,故应选择第二种进货方案.
【学习目标】
1.经历建立方程模型、解方程和运用方程解决实际问题的过程,体会模型思想;
2.了解一元一次方程、方程的解等基本概念,会解数字系数的一元一次方程,感受转化思想;
3.能运用一元一次方程解决实际问题,能根据实际意义检验方程的解的合理性.
【知识网络】
【要点梳理】
要点一、一元一次方程的概念
1.方程:含有未知数的等式叫做方程.
2.一元一次方程:只含有一个未知数(元),未知数的次数都是1,这样的方程叫做一元一次方程.
要点诠释:
(1)一元一次方程变形后总可以化为ax+b=0(a≠0)的形式,它是一元一次方程的标准形式.
(2)判断是否为一元一次方程,应看是否满足:①只含有一个未知数,未知数的次数为1;
②未知数所在的式子是整式,即分母中不含未知数.
3.方程的解:使方程的左、右两边相等的未知数的值叫做这个方程的解.
4.解方程:求方程的解的过程叫做解方程.
要点二、等式的性质与去括号法则
1.等式的性质:
等式的性质1:等式两边同时加上(或减去)同一个代数式,所得结果仍是等式.
等式的性质2:等式两边乘同一个数,(或除以同一个不为0的数),所得结果仍是等式.
2.合并法则:合并时,把系数相加(减)作为结果的系数,字母和字母的指数保持不变.
3.去括号法则:
(1)括号外的因数是正数,去括号后各项的符号与原括号内相应各项的符号相同.
(2)括号外的因数是负数,去括号后各项的符号与原括号内相应各项的符号相反.
要点三、一元一次方程的解法
解一元一次方程的一般步骤:
(1)去分母:在方程两边同乘以各分母的最小公倍数.
(2)去括号:依据乘法分配律和去括号法则,先去小括号,再去中括号,最后去大括号.
(3)移项:把含有未知数的项移到方程一边,常数项移到方程另一边.
(4)合并:逆用乘法分配律,分别合并含有未知数的项及常数项,把方程化为ax=b(a≠0)的形式.
(5)系数化为1:方程两边同除以未知数的系数得到方程的解(a≠0).
(6)检验:把方程的解代入原方程,若方程左右两边的值相等,则是方程的解;若方程左右两边的值不相等,则不是方程的解.
要点四、用一元一次方程解决实际问题的常见类型
1.等积变形:①形状面积变了,周长没变;②原体积=变化后体积.
2.利润问题:商品利润=商品售价-商品进价
3.行程问题:路程=速度×时间
4.和差倍分问题:增长量=原有量×增长率
5.工程问题:工作量=工作效率×工作时间,各部分劳动量之和=总量
6.银行存贷款问题:本息和=本金+利息,利息=本金×利率×期数
7.数字问题:多位数的表示方法:例如:.
8.方案问题:(1)运用一元一次方程解应用题的方法求解两种方案值相等的情况.
(2)用特殊值试探法选择方案,取小于(或大于)一元一次方程解的值,比较两种方案的优劣性后下结论.
【典型例题】
类型一、一元一次方程的相关概念
1.已知方程(3m-4)x2-(5-3m)x-4m=-2m是关于x的一元一次方程,求m和x的值.
【思路点拨】若一个整式方程经过化简变形后,只含有一个未知数,并且未知数的次数都是1,系数不为0,则这个方程是一元一次方程.
【答案与解析】
解:因为方程(3m-4)x2-(5-3m)x-4m=-2m是关于x的一元一次方程,
所以3m-4=0且5-3m≠0.
由3m-4=0解得,又能使5-3m≠0,所以m的值是.
将代入原方程,则原方程变为,解得.
所以,.
【总结升华】解答这类问题,一定要严格按照一元一次方程的定义.方程(3m-4)x2-(5-3m)x-4m=-2m2是关于x的一元一次方程,就是说x的二次项系数3m-4=0,而x的一次项系数5-3m≠0,m的值必须同时符合这两个条件.
举一反三:
【变式】下面方程变形中,错在哪里:
(1)方程2x=2y两边都减去x+y,得2x-(x+y)=2y-(x+y), 即x-y=-(x-y).
方程 x-y=-(x-y)两边都除以x-y, 得1=-1.
(2),去分母,得3(3-7x)=2(2x+1)+2x,去括号得:9-21x=4x+2+2x.
【答案】(1)答:错在第二步,方程两边不能除以x-y,只有一种可能就是x-y为0了,所以出现了1=-1的错误,也就是说对于等式性质来说,如果想要除以式子来说,这个式子一定是不能为0的.
(2)答:错在第一步,去分母时2x项没乘以公分母6.
2. (2015秋?营山县校级期中)对于ax+b=0(a,b为常数),表述正确的是( )
A.当a≠0时,方程的解是x= B.当a=0,b≠0时,方程有无数解
C.当a=0,b=0,方程无解 D.以上都不正确
【答案】D.
【解析】
解:A、当a≠0时,方程的解是x=﹣,故错误;
B、当a=0,b≠0时,方程无解,故错误;
C、当a=0,b=0,方程有无数解,故错误;
D、以上都不正确.
【总结升华】此题很简单,解答此题的关键是:正确记忆一元一次方程的一般形式中,一次项系数不等于0.
举一反三:
【变式】已知|x+1|+(y+2x)2=0,则________.
【答案】1
类型二、一元一次方程的解法
3.解方程:解方程3{2x-1-[3(2x-1)+3]}=5.
【答案与解析】
解:把2x-1看做一个整体.去括号,得:
3(2x-1)-9(2x-1)-9=5.
合并同类项,得-6(2x-1)=14.
系数化为1得: ,
解得 .
【总结升华】把题目中的2x-1看作一个整体,从而简化了计算过程.本题也可以考虑换元法:设2x-1=a,则原方程化为3[a-(3a+3)]=5.
举一反三:
【变式】解方程
【答案】
解:把方程两边含有分母的项化整为零,得
.
移项,合并同类项得:,
系数化为1得: z=1.
类型三、特殊的一元一次方程的解法
1.解含字母系数的方程
4.解关于的方程:
【思路点拨】这个方程化为标准形式后,未知数x的系数和常数都是以字母形式出现的,所以方程的解的情况与x的系数和常数的取值都有关系.
【答案与解析】
解:原方程可化为:
当时,原方程有唯一解:;
当时,原方程无数个解;
当时,原方程无解;
【总结升华】解含字母系数的方程时,一般化为最简形式,再分类讨论进行求解,注意最后的解不能合并,只能分情况说明.
2.解含绝对值的方程
5. 解方程|x-2|=3.
【答案与解析】
解:当x-2≥0时,原方程可化为x-2=3,得x=5.
当x-2<0时,原方程可化为-(x-2)=3,得 x=-1.
所以x=5和x=-1都是方程|x-2|=3的解.
【总结升华】如图所示,可以看出点-1与5到点2的距离均为3,所以|x-2|=3的意义为在数轴上到点2的距离等于3的点对应的数,即方程|x-2|=3的解为x=-1和x=5.
举一反三:
【变式】若关于的方程无解,只有一个解,有两个解,
则的大小关系为: ( )
A. B. C. D.
【答案】A
类型四、一元一次方程的应用
6.李伟从家里骑摩托车到火车站,如果每小时行30千米,那么比火车开车时间早到15分钟;若每小时行18千米,则比火车开车时间迟到15分钟,现在李伟打算在火车开车前10分钟到达火车站,求李伟此时骑摩托车的速度应是多少?
【思路点拨】本题中的两个不变量为:火车开出的时间和李伟从家到火车站的路程不变.
【答案与解析】
解:设李伟从家到火车站的路程为y千米,则有:
,解得:
由此得到李伟从家出发到火车站正点开车的时间为(小时).
李伟打算在火车开车前10分钟到达火车站时,设李伟骑摩托车的速度为x千米/时, 则有:
(千米/时)
答:李伟此时骑摩托车的速度应是27千米/时.
【总结升华】在解决问题时,当发现某种方法不能解决问题时,应该及时变换思维角度,如本题直接设未知数较难时,应迅速变换思维的角度,合理地设置间接未知数以寻求新的解决问题的途径和方法.
7. 黄冈某地“杜鹃节”期间,某公司70名职工组团前往参观欣赏,旅游景点规定:①门票每人60元,无优惠;②上山游玩可坐景点观光车,观光车有四座和十一座车,四座车每辆60元,十一座车每人10元.公司职工正好坐满每辆车且总费用刚好为4920元时,问公司租用的四座车和十一座车各多少辆?
【答案与解析】
解:设四座车租x辆,十一座车租辆,依题意得:
解得:x=1,
答:公司租用的四座车和十一座车分别是1辆和6辆.
【总结升华】解答本题需从“公司职工正好坐满每辆车且总费用刚好为4920元”中挖掘两个等量关系构建方程求解.
8.某牛奶加工厂有鲜奶9吨,若在市场上直接销售鲜奶,每吨可获取利润500元,制成酸奶销售,每吨可获取利润1200元;制成奶片销售,每吨可获利润2000元,该工厂的生产能力是:如制成酸奶,每天可加工3吨;制成奶片每天可加工1吨,受人员限制,两种加工方式不可同时进行,受气温条件限制,这批牛奶必须在4天内全部销售或加工完毕.为此,该厂某领导提出了两种可行方案:
方案1:尽可能多的制成奶片,其余直接销售鲜牛奶;
方案2:将一部分制成奶片,其余制成酸奶销售,并恰好4天完成.
你认为选择哪种方案获利最多,为什么?
【答案与解析】
解:(1)若选择方案1,依题意,
总利润=2000元×4+500元×(9-4)=10500(元).
(2)若选择方案2.
方法一:
解:设将x吨鲜奶制成奶片,则用(9-x)吨鲜奶制成酸奶销售.
依题意得,,
解得.
当时,.
总利润=2000×1.5+1200×7.5=12000(元).
∵ 12000>10500,
∴ 选择方案2较好.
方法二:
解:设x天生产奶片,则(4-x)天生产酸奶.
x+3(4-x)=9
x=1.5
4-x=2.5
1.5×1×2000+2.5×3×1200=12000(元)
∵ 12000>10500,
∴ 选择方案2较好.
答:选择方案2获利最多,只要在四天内用7.5吨鲜奶加工成酸奶,用1.5吨的鲜奶加工成奶片.
【总结升华】如果题目中的数量关系较复杂,常借助列表,画线段图,示意图等手段帮助我们理顺题目中的数量关系,列出方程.例如本题方案2中的方法一,设将x吨鲜奶制成奶片,则列表如下:
每吨利润
吨数
工效
天数
酸奶
1200
3
奶片
2000
1
合计
9
4
该表可以使条件之间的关系一目了然,从而得到等量关系,当然此题也可以设天数来计算,同学们可根据理解自己选择.
举一反三:
【变式】(2015?吴江市一模)现有甲、乙两种金属的合金10kg,如果加入甲种金属若干,那么重新熔炼后的合金中乙种金属占2份,甲种金属占3份,如果加入的甲种金属是第一次加入的2倍,那么重新熔炼后的合金中乙种金属占3份,甲种金属占7份,第一次加入的甲种金属多少?原来这块合金中甲种金属的百分比是多少?
【答案】
解:设原来这块合金中甲种金属的百分比是x,则甲种金属有10xkg,乙种金属有(10﹣10x)kg,根据题意得
(10﹣10x)÷﹣10=2×[(10﹣10x)÷﹣10],
解得x=40%.
则(10﹣10×40%)÷﹣10=5(kg).
答:第一次加入的甲种金属是5kg,原来这块合金中甲种金属的百分比是40%.
【巩固练习】
一、选择题
1.已知方程是关于x的一元一次方程,则m的值是( ).
A.±1 B.1 C.-1 D.0或1
2.已知是方程的解,那么关于y的方程的解是( ).
A.y=1 B.y=-1 C.y=0 D.方程无解
3.已知,则等于( ).
A. B. C. D.
4.一列火车长100米,以每秒20米的速度通过800米长的隧道,从火车进入隧道起,至火车完全通过所用的时间为( ).
A.50秒 B.40秒 C.45秒 D.55秒
5.一架飞机在两城间飞行,顺风要5.5小时,逆风要6小时,风速为24千米/时,求两城距离x的方程是( ).
A. B.
C. D.
6.(2015?永州)永州市双牌县的阳明山风光秀丽,历史文化源远流长,尤以山顶数万亩野生杜鹃花最为壮观,被誉为“天下第一杜鹃红”.今年“五一”期间举办了“阳明山杜鹃花旅游文化节”,吸引了众多游客前去观光赏花.在文化节开幕式当天,从早晨8:00开始每小时进入阳明山景区的游客人数约为1000人,同时每小时走出景区的游客人数约为600人,已知阳明上景区游客的饱和人数约为2000人,则据此可知开幕式当天该景区游客人数饱和的时间约为( )
A.10:00 B.12:00 C.13:00 D.16:00
7.某书中一道方程题:,□处在印刷时被墨盖住了,查书后面的答案,得知这个方程的解是x=﹣2.5,那么□处应该是数字( ).
A.-2.5 B.2.5 C.5 D.7
8. 已知:,,,,…,
若符合前面式子的规律,则a+b的值为( ).
A. 179 B. 140 C. 109 D. 210
二、填空题
9.已知方程是关于x的一元一次方程,则这个方程的解为________.
10.已知和互为相反数,则________.
11.(2015?温州校级自主招生)对于实数a,b,c,d,规定一种数的运算:=ad﹣bc,那么当=10时,x= .
12.一商店把某商品按标价的九折出售仍可获得20%的利润率,若该商品的进价是每件30元,则标价是每件 元.
13.某种中草药含甲、乙、丙、丁四种草药成分,这四种草药成分的质量比是0.7∶1∶2∶
4.7.现在要配制这种中药1400克,这四种草药分别需要多少克?设每份为克,根据题意,得 .
14.有一列数,按一定的规律排列:―1,2,―4,8,―16,32,―64,128,…,其中某三个相邻数之和为384,这三个数分别是 .
15.已知关于的方程和方程有相同的解,则该方程的解为 .
16. x表示一个两位数, y表示一个三位数, 若把x放在y的左边组成一个五位数记作M1, 把y放在x的左边组成一个五位数记作M2, 则 M1 ( M2 是 的倍数.
三、解答题
17.解方程:
(1).
(2) .
(3)|3x-2|-4=0 .
18.探究:当b为何值时,方程|x-2|=b+1 ① 无解;②只有一个解;③ 有两个解.
19.(2015?海淀区二模)小明坚持长跑健身.他从家匀速跑步到学校,通常需30分钟.某周日,小明与同学相约早上八点学校见,他七点半从家跑步出发,平均每分钟比平时快了40米,结果七点五十五分就到达了学校,求小明家到学校的距离.
20.商场计划拨款9万元,从厂家购进50台电视机,已知该厂家生产三种不同型号的电视机,出场价分别为甲种每台1500元,乙种每台2100元,丙种每台2500元.
(1)若商场同时购进其中两种不同型号的电视机共50台,用去9万元,请你研究一下商场的进货方案;(2)若商场销售一台甲种电视机可获利150元,销售一台乙种电视机可获利200元,销售一台丙种电视机可获利250元.在同时购进两种不同型号的电视机的方案中,为使销售时获利最多,该选择哪种进货方案?
【答案与解析】
一、选择题
1. 【答案】B
【解析】由题意得|m|=1,且m+1≠0,所以m=1,故选B.
2. 【答案】C
【解析】由x=1是方程的解,可代入求出a的值,然后把a的值代入方程a(y+4)=2ay+4a中,求出y的值.
3. 【答案】D
【解析】由原式可得:,将“”看作整体,合并化简即可.
4.【答案】C
【解析】相等关系是:火车所走的路程=火车长度+隧道长度.设火车完全通过所用时间为x秒,可得方程20x=100+800,解得x=45.
5. 【答案】A
【解析】解:∵两城距离为x,顺风要5.5小时,逆风要6小时,
∴顺风速度=,逆风速度=,
∵风速为24千米/时,
∴可列方程为:
6.【答案】C.
【解析】设开幕式当天该景区游客人数饱和的时间约为x点,则
(x﹣8)×(1000﹣600)=2000,解得x=13.
即开幕式当天该景区游客人数饱和的时间约为13:00.
7.【答案】C
【解析】把x=-2.5代入方程,再把□当作未知数解方程即可.
8.【答案】C
【解析】观察规律可得b=10,a=b2-1=99,所以a+b=109.
二、填空题
9.【答案】x=1
【解析】首先将原方程整理成的形式,由一元一次方程的定义可知,二次项系数为0,所以a=5,代入方程中即可求出x的值.
10.【答案】-8
【解析】两数互为相反数,则和为0,由非负数的性质可知m-n+4=0,且n-3=0.从而得m=-1,n=3.
11.【答案】﹣1.
【解析】由题意得,2x+12=10,解得x=﹣1.故答案为:﹣1.
12.【答案】40
【解析】解:设标价为元,则有,解得:
13.【答案】
14.【答案】128,-256,512
【解析】通过观察可得:第个数为:,所以第9,10个数分别为:,经检验满足题意.
15.【答案】
【解析】分别解得这两个关于x的方程的解为,,由它们相等得,代入其中一解可得答案.
16.【答案】9
【解析】M1=1000x+y,M2=100y+x,M1 ( M2=9(111x-11y),所以一定是9的倍数.
三、解答题
17.【解析】
解:(1)整理,得,
去分母,得,
去括号,得,
移项,得,
合并,得,
系数化为1,得.
(2)原方程可化为:
解得:x=
(3)原式可化为:|3x-2|=4
由,可得:;由,可得:
所以原方程的解为:x=2,x=-.
18. 【解析】
解:①当,即 b<-1时,原方程无解;
②当,即 b=-1时,原方程只有一个解;
③ 当,即b>-1时,原方程有两个解.
19.【解析】
解:设小明家到学校的距离为x米,
由题意,得+40=,
解得x=6000.
答:小明家到学校的距离为6000米.
20.【解析】
解:(1)①解:设购进甲种电视机台,则购进乙种电视机(50-)台,根据题意,得
1500+2100(50-)=90000.
解得: =25,则50-=25.
故第一种进货方案是购甲、乙两种型号的电视机各25台.
②设购进甲种电视机台,则购进丙种电视机(50- )台,根据题意,得
1500+2500(50-)=90000.
解得: =35,则50-=15.
故第二种进货方案是购进甲种电视机35台,丙种电视机15台.
③设购进乙种电视机台,则购进丙种电视机(50-)台,购进题意,得
2100+2500(50-)=90000.
解得: =87.5(不合题意).
故此种方案不可行.
(2)上述的第一种方案可获利:150×25+200×25=8750元,
第二种方案可获利:150×35+250×15=9000元,
因为8750<9000,故应选择第二种进货方案.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
