高中数学新人教A版必修4课件:第一章三角函数1.1.1任意角:30张PPT
文档属性
| 名称 | 高中数学新人教A版必修4课件:第一章三角函数1.1.1任意角:30张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 296.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-19 10:33:47 | ||
图片预览










文档简介
课件30张PPT。第一章 三角函数
1.1 任意角和弧度制
1.1.1 任意角课标要求:1.了解任意角的概念及角的分类.2.理解象限角的概念.3.理解终边相同的角的概念,并能熟练写出终边相同的角的集合表示.自主学习 1.任意角的概念
(1)角的概念
角可以看成平面内一条射线绕着端点从一个位置 到另一个位置所成的图形,如图所示,∠AOB(或∠O或α)中角的顶点是O.角的始边是射线OA,角的终边是射线OB.知识探究旋转(2)角的分类
按旋转方向可将角分为如下三类:
①正角:按 方向旋转形成的角;
②负角:按顺时针方向旋转形成的角;
③零角:如果一条射线没有作任何旋转,我们称它形成了一个零角.
2.象限角
(1)在直角坐标系中研究角时,如果角的顶点与 重合,角的始边与x轴的非负半轴重合,那么,角的终边在第几象限,我们就说这个角是第几象限角.如果角的终边 上,就认为这个角不属于任何一个象限.
(2)终边落在x轴的非负半轴和y轴的非正半轴上的角的集合分别为
{α|α=k·360°,k∈Z};{α|α=k·360°+270°,k∈Z}.逆时针原点坐标轴3.终边相同的角
所有与角α终边相同的角,连同角α在内,可构成一个集合S=
,即任一与角α终边相同的角,都可以表示成角α与整数个周角的和.
【拓展延伸】
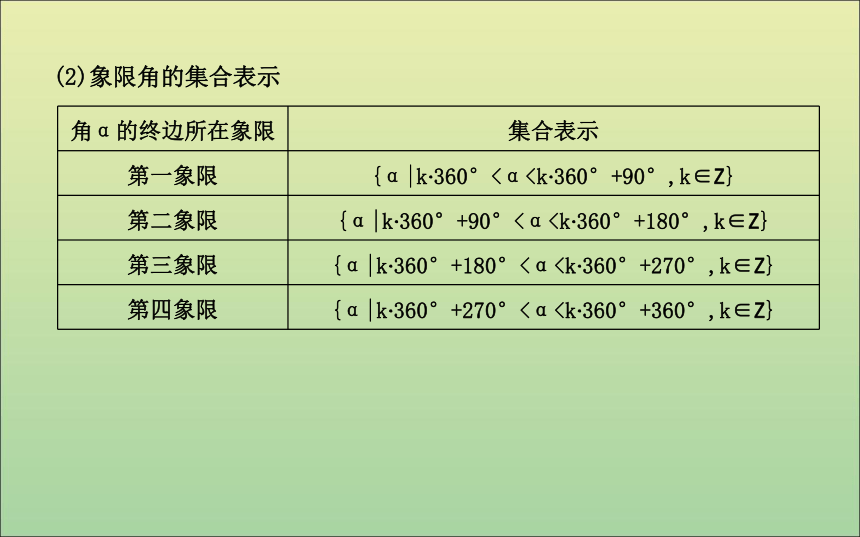
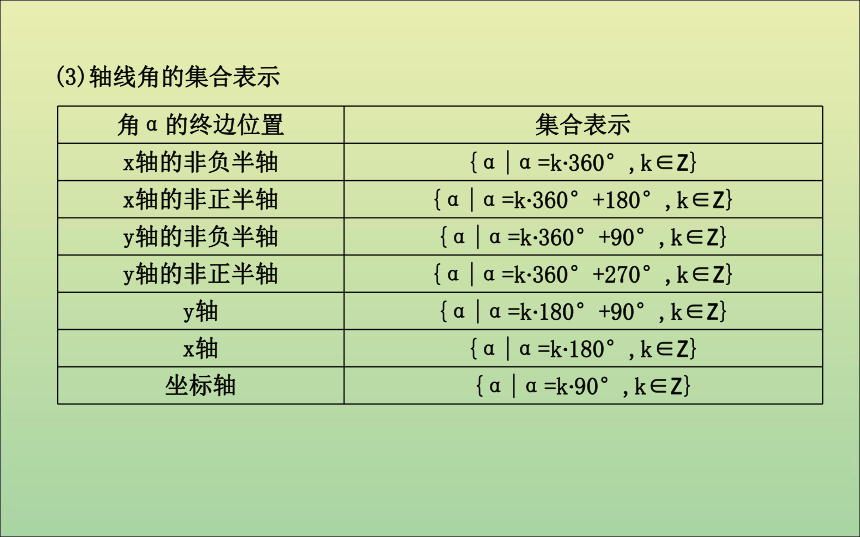
(1)锐角、0°~90°的角、小于90°的角及第一象限角的区别{β|β=α+k·360°,k∈Z}(2)象限角的集合表示(3)轴线角的集合表示1.以下表示第一象限角的集合的是( )
(A){x|0°(B){x|k·360°≤x≤k·360°+90°,k∈Z}
(C){x|k·360°-90°(D){x|k·360°(A)A=B (B)B=C
(C)A=C (D)A=DD3.若β是第二象限角,则270°+β是( )
(A)第一象限角 (B)第二象限角
(C)第三象限角 (D)第四象限角A解析:由于β是第二象限角,所以k·360°+90°<βk∈Z,则(k+1)·360°<β+270°<(k+1)·360°+90°,k∈Z,所以
270°+β是第一象限角,故选A.4.855°是第 象限角.?答案:二5.集合M={α=k·90°,k∈Z}中,各角的终边在 上.?答案:x轴或y轴题型一 终边相同的角及象限角课堂探究【例1】 (1)将下列各角表示为k·360°+α(k∈Z,0°≤α<360°)的形式,并指出是第几象限角.
①420°;②-510°;③1 020°.解:(1)①420°=360°+60°,
而60°角是第一象限角,故420°是第一象限角.
②-510°=-2×360°+210°,
而210°是第三象限角,故-510°是第三象限角.
③1 020°=2×360°+300°,
而300°是第四象限角,故1 020°是第四象限角.(2)在与角1 030°终边相同的角中,求满足下列条件的角.
①最小的正角;
②最大的负角.解:(2)1 030°÷360°=2……310°,
所以1 030°=2×360°+310°,
所以与角1 030°终边相同的角的集合为
{α|α=k·360°+310°,k∈Z}.
①故所求的最小正角为310°.
②取k=-1得所求的最大负角为-50°.误区警示 在利用β=α+k·360°(k∈Z)判断β所在象限时,一定要注意0°≤α<360°,这样只需判断α所在的象限即可.即时训练1-1:(1)写出终边在如图所示直线上的角的集合;解:(1)①在0°~360°范围内,终边在x轴上的角有两个,
即0°和180°,
因此所有与0°角的终边相同的角构成集合S1={β|β=0°+k·360°,k∈Z},而所有与180°的终边相同的角构成集合S2={β|β=180°+k·360°,k∈Z}.于是,终边落在x轴上的角的集合S=S1∪S2={β|β=k·180°,k∈Z}.
②在0°~360°范围内,终边在直线y=-x上的角有两个,即135°和315°.因此,终边在直线y=-x上的角的集合S={β|β=135°+k·360°,k∈Z}∪{β|β
=315°+k·360°,k∈Z}={β|β=135°+k·180°,k∈Z}.
③终边在直线y=x上的角的集合为{β|β=45°+k·180°,k∈Z},于是所求角的集合S={β|β=45°+k·180°,k∈Z}∪{β|β=135°+k·180°,k∈Z}=
{β|β=45°+2k·90°,k∈Z}∪{β|β=45°+(2k+1)·90°,k∈Z}=
{β|β=45°+k·90°,k∈Z}.(2)已知α=-1 845°,在与α终边相同的角中,求满足下列条件的角.
①最小的正角;
②最大的负角;
③-360°~720°之间的角.解:(2)因为-1 845°=-45°+(-5)×360°,
即-1 845°角与-45°角的终边相同,
所以与角α终边相同的角的集合是
{β|β=-45°+k·360°,k∈Z}.
①最小的正角为315°.
②最大的负角为-45°.
③-360°~720°之间的角分别是-45°,315°,675°.题型二 区域角的表示解:终边与OA重合的最小正角为30°,故终边落在OA上的角的集合为
{α|α=30°+k·360°,k∈Z}.
同理,终边与OB重合的最小正角为60°,故终边落在OB上的角的集合为
{β|β=60°+k·360°,k∈Z}.
由题图可知,阴影部分区域可表示为
{γ|30°+k·360°≤γ≤60°+k·360°,k∈Z}.【例2】写出终边落在阴影部分(包括边界)的角的集合.变式探究:把例2图形中的阴影部分(包括边界)变为如图,再写出终边落在阴影部分的角的集合.解:图中阴影部分在第一象限的为k·360°+30°≤α≤k·360°+90°,
在第三象限的为k·360°+210°≤α≤k·360°+270°,
则两部分合为
{α|k·180°+30°≤α≤k·180°+90°,k∈Z}.方法技巧 表示区域角的步骤:
(1)先按逆时针方向找到区域的起始和终止边界.
(2)写出以起始、终止边界为终边的角.
(3)根据角的大小关系写出表示区域角的集合或区间.
求解最后结果需注意边界线的虚实,即表示区域角的区间的开闭.即时训练2-1:(1)如图所示,写出顶点在原点,始边重合于x轴的非负半轴,终边落在阴影部分内的角的集合;(1)解:①以OB为终边的角是330°,可看成-30°,
所以以OA,OB为终边的角的集合分别是S1={x|x=75°+k·360°,k∈Z},S2={x|x=-30°+k·360°,k∈Z},
所以终边落在阴影部分内的角的集合为
{θ|k·360°-30°≤θ≤k·360°+75°,k∈Z}.
②设终边落在阴影部分的角为α,角α的集合由两部分组成.
(ⅰ){α|k·360°+30°≤α(ⅱ){α|k·360°+210°≤α所以角α的集合应当是集合(ⅰ)与(ⅱ)的并集;
{α|k·360°+30°≤α . (2)解析:终边与OB重合的最小正角为30°,故终边落在OB上的角的集合为{β|β=30°+k·360°,k∈Z},
终边与OA重合的最大负角为-60°,故终边落在OA上的角的集合为{γ|γ=-60°+k·360°,k∈Z}.
则角α的取值范围为{α|-60°+k·360°≤α≤30°+k·360°,k∈Z}.
答案:{α|-60°+k·360°≤α≤30°+k·360°,k∈Z}题型三 判断角所在的象限即时训练3-1:(1)已知角α的终边与-770°角的终边关于y轴对称,则角α的终边在第 象限.?(1)解析:-770°=310°+(-3)×360°
=40°+270°+(-3)×360°,
由已知条件可知角α的终边与270°-40°=230°角的终边相同,故α=230°+k·360°,k∈Z.
因为230°角的终边在第三象限,
所以角α终边在第三象限.
答案:三②角2α终边的位置.解:②因为180°+k·360°<α<270°+k·360°(k∈Z),
所以360°+2k·360°<2α<540°+2k·360°(k∈Z),
即角2α终边在第一象限或第二象限或y轴的正半轴.
1.1 任意角和弧度制
1.1.1 任意角课标要求:1.了解任意角的概念及角的分类.2.理解象限角的概念.3.理解终边相同的角的概念,并能熟练写出终边相同的角的集合表示.自主学习 1.任意角的概念
(1)角的概念
角可以看成平面内一条射线绕着端点从一个位置 到另一个位置所成的图形,如图所示,∠AOB(或∠O或α)中角的顶点是O.角的始边是射线OA,角的终边是射线OB.知识探究旋转(2)角的分类
按旋转方向可将角分为如下三类:
①正角:按 方向旋转形成的角;
②负角:按顺时针方向旋转形成的角;
③零角:如果一条射线没有作任何旋转,我们称它形成了一个零角.
2.象限角
(1)在直角坐标系中研究角时,如果角的顶点与 重合,角的始边与x轴的非负半轴重合,那么,角的终边在第几象限,我们就说这个角是第几象限角.如果角的终边 上,就认为这个角不属于任何一个象限.
(2)终边落在x轴的非负半轴和y轴的非正半轴上的角的集合分别为
{α|α=k·360°,k∈Z};{α|α=k·360°+270°,k∈Z}.逆时针原点坐标轴3.终边相同的角
所有与角α终边相同的角,连同角α在内,可构成一个集合S=
,即任一与角α终边相同的角,都可以表示成角α与整数个周角的和.
【拓展延伸】
(1)锐角、0°~90°的角、小于90°的角及第一象限角的区别{β|β=α+k·360°,k∈Z}(2)象限角的集合表示(3)轴线角的集合表示1.以下表示第一象限角的集合的是( )
(A){x|0°
(C){x|k·360°-90°
(C)A=C (D)A=DD3.若β是第二象限角,则270°+β是( )
(A)第一象限角 (B)第二象限角
(C)第三象限角 (D)第四象限角A解析:由于β是第二象限角,所以k·360°+90°<β
270°+β是第一象限角,故选A.4.855°是第 象限角.?答案:二5.集合M={α=k·90°,k∈Z}中,各角的终边在 上.?答案:x轴或y轴题型一 终边相同的角及象限角课堂探究【例1】 (1)将下列各角表示为k·360°+α(k∈Z,0°≤α<360°)的形式,并指出是第几象限角.
①420°;②-510°;③1 020°.解:(1)①420°=360°+60°,
而60°角是第一象限角,故420°是第一象限角.
②-510°=-2×360°+210°,
而210°是第三象限角,故-510°是第三象限角.
③1 020°=2×360°+300°,
而300°是第四象限角,故1 020°是第四象限角.(2)在与角1 030°终边相同的角中,求满足下列条件的角.
①最小的正角;
②最大的负角.解:(2)1 030°÷360°=2……310°,
所以1 030°=2×360°+310°,
所以与角1 030°终边相同的角的集合为
{α|α=k·360°+310°,k∈Z}.
①故所求的最小正角为310°.
②取k=-1得所求的最大负角为-50°.误区警示 在利用β=α+k·360°(k∈Z)判断β所在象限时,一定要注意0°≤α<360°,这样只需判断α所在的象限即可.即时训练1-1:(1)写出终边在如图所示直线上的角的集合;解:(1)①在0°~360°范围内,终边在x轴上的角有两个,
即0°和180°,
因此所有与0°角的终边相同的角构成集合S1={β|β=0°+k·360°,k∈Z},而所有与180°的终边相同的角构成集合S2={β|β=180°+k·360°,k∈Z}.于是,终边落在x轴上的角的集合S=S1∪S2={β|β=k·180°,k∈Z}.
②在0°~360°范围内,终边在直线y=-x上的角有两个,即135°和315°.因此,终边在直线y=-x上的角的集合S={β|β=135°+k·360°,k∈Z}∪{β|β
=315°+k·360°,k∈Z}={β|β=135°+k·180°,k∈Z}.
③终边在直线y=x上的角的集合为{β|β=45°+k·180°,k∈Z},于是所求角的集合S={β|β=45°+k·180°,k∈Z}∪{β|β=135°+k·180°,k∈Z}=
{β|β=45°+2k·90°,k∈Z}∪{β|β=45°+(2k+1)·90°,k∈Z}=
{β|β=45°+k·90°,k∈Z}.(2)已知α=-1 845°,在与α终边相同的角中,求满足下列条件的角.
①最小的正角;
②最大的负角;
③-360°~720°之间的角.解:(2)因为-1 845°=-45°+(-5)×360°,
即-1 845°角与-45°角的终边相同,
所以与角α终边相同的角的集合是
{β|β=-45°+k·360°,k∈Z}.
①最小的正角为315°.
②最大的负角为-45°.
③-360°~720°之间的角分别是-45°,315°,675°.题型二 区域角的表示解:终边与OA重合的最小正角为30°,故终边落在OA上的角的集合为
{α|α=30°+k·360°,k∈Z}.
同理,终边与OB重合的最小正角为60°,故终边落在OB上的角的集合为
{β|β=60°+k·360°,k∈Z}.
由题图可知,阴影部分区域可表示为
{γ|30°+k·360°≤γ≤60°+k·360°,k∈Z}.【例2】写出终边落在阴影部分(包括边界)的角的集合.变式探究:把例2图形中的阴影部分(包括边界)变为如图,再写出终边落在阴影部分的角的集合.解:图中阴影部分在第一象限的为k·360°+30°≤α≤k·360°+90°,
在第三象限的为k·360°+210°≤α≤k·360°+270°,
则两部分合为
{α|k·180°+30°≤α≤k·180°+90°,k∈Z}.方法技巧 表示区域角的步骤:
(1)先按逆时针方向找到区域的起始和终止边界.
(2)写出以起始、终止边界为终边的角.
(3)根据角的大小关系写出表示区域角的集合或区间.
求解最后结果需注意边界线的虚实,即表示区域角的区间的开闭.即时训练2-1:(1)如图所示,写出顶点在原点,始边重合于x轴的非负半轴,终边落在阴影部分内的角的集合;(1)解:①以OB为终边的角是330°,可看成-30°,
所以以OA,OB为终边的角的集合分别是S1={x|x=75°+k·360°,k∈Z},S2={x|x=-30°+k·360°,k∈Z},
所以终边落在阴影部分内的角的集合为
{θ|k·360°-30°≤θ≤k·360°+75°,k∈Z}.
②设终边落在阴影部分的角为α,角α的集合由两部分组成.
(ⅰ){α|k·360°+30°≤α
{α|k·360°+30°≤α
终边与OA重合的最大负角为-60°,故终边落在OA上的角的集合为{γ|γ=-60°+k·360°,k∈Z}.
则角α的取值范围为{α|-60°+k·360°≤α≤30°+k·360°,k∈Z}.
答案:{α|-60°+k·360°≤α≤30°+k·360°,k∈Z}题型三 判断角所在的象限即时训练3-1:(1)已知角α的终边与-770°角的终边关于y轴对称,则角α的终边在第 象限.?(1)解析:-770°=310°+(-3)×360°
=40°+270°+(-3)×360°,
由已知条件可知角α的终边与270°-40°=230°角的终边相同,故α=230°+k·360°,k∈Z.
因为230°角的终边在第三象限,
所以角α终边在第三象限.
答案:三②角2α终边的位置.解:②因为180°+k·360°<α<270°+k·360°(k∈Z),
所以360°+2k·360°<2α<540°+2k·360°(k∈Z),
即角2α终边在第一象限或第二象限或y轴的正半轴.
