高中数学新人教A版必修4课件:第一章三角函数1.2.2同角三角函数的基本关系:28张PPT
文档属性
| 名称 | 高中数学新人教A版必修4课件:第一章三角函数1.2.2同角三角函数的基本关系:28张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-19 00:00:00 | ||
图片预览








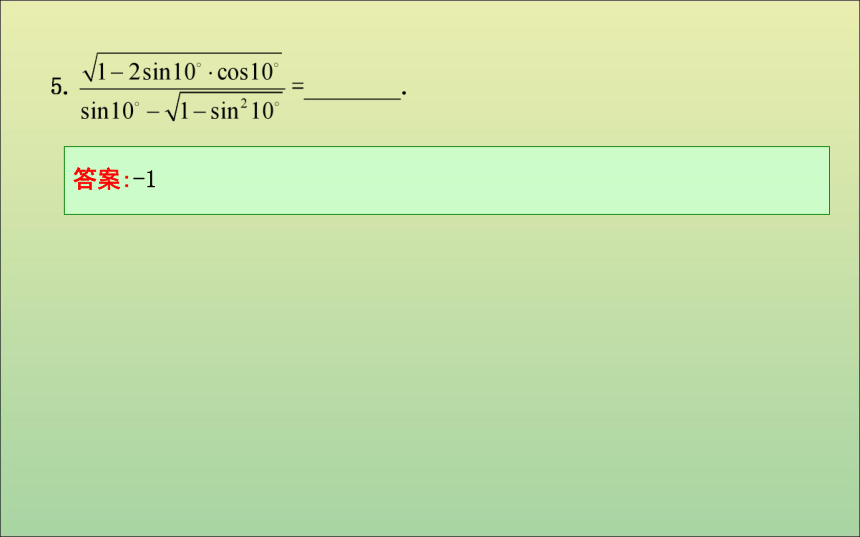
文档简介
课件28张PPT。1.2.2 同角三角函数的基本关系课标要求:1.理解同角三角函数基本关系:sin2α+cos2α=1, =tanα.
2.能灵活运用同角三角函数基本关系进行化简、求值、证明.自主学习 1.平方关系:sin2α+cos2α=1.
这个关系对于任意角都是成立的.现在用正、余弦函数的定义证明如下:知识探究3.对同角三角函数基本关系式的理解
(1)注意“同角”,这里“同角”有两层含义,一是“角相同”,二是对“任意”一个角(在使函数有意义的前提下)关系式都成立,即与角的表达形式无关,如sin23α+cos23α=1成立,但是sin2α+cos2β=1就不一定成立.
(2)sin2α是(sin α)2的简写,读作“sin α的平方”,不能将sin2α写成
sin α2,前者是α的正弦的平方,后者是α2的正弦,两者是不同的,要弄清它们的区别,并能正确书写.1.化简 的结果是( )自我检测CD3.设A是△ABC的一个内角,且sin A+cos A= ,则这个三角形是( )
(A)锐角三角形 (B)钝角三角形
(C)等边三角形 (D)等腰直角三角形B4.化简: = .?答案:cos θ答案:-1题型一 已知角的一个三角函数值,求其他三角函数值课堂探究题型二 已知角的正切值,求同角三角函数式的值【例2】 设tan α=2,求下列各式的值:(2)2sin2α-3sin αcos α+5cos2α.方法技巧 化切求值的方法(2)对于asin2α+bsin αcos α+ccos2α的求值,可看成分母是1,利用1=
sin2α+cos2α进行代替后分子分母同时除以cos2α,得到关于tan α的式子,从而可以求值.(2)cos2x-sin xcos x.题型三 sin θ±cos θ与sin θcos θ之间的联系(2)求sin α-cos α的值.误区警示 在利用sin α±cos α与sin αcos α的关系求值时,一定注意判断它们的符号,否则就会出现漏解或错解.答案:-2题型四 三角函数式的化简与证明题后反思 利用同角三角函数关系式化简的方法
①化切为弦,减少函数名称,便于约分化简;②对含根号的,应先把被开方式化为完全平方,去掉根号,为防止出错,去掉根号后首先用绝对值号表示,然后考虑正负,以保证万无一失;③对含有高次的三角函数式,可借助于因式分解,或构造平方关系,以便于降幂化简.
2.能灵活运用同角三角函数基本关系进行化简、求值、证明.自主学习 1.平方关系:sin2α+cos2α=1.
这个关系对于任意角都是成立的.现在用正、余弦函数的定义证明如下:知识探究3.对同角三角函数基本关系式的理解
(1)注意“同角”,这里“同角”有两层含义,一是“角相同”,二是对“任意”一个角(在使函数有意义的前提下)关系式都成立,即与角的表达形式无关,如sin23α+cos23α=1成立,但是sin2α+cos2β=1就不一定成立.
(2)sin2α是(sin α)2的简写,读作“sin α的平方”,不能将sin2α写成
sin α2,前者是α的正弦的平方,后者是α2的正弦,两者是不同的,要弄清它们的区别,并能正确书写.1.化简 的结果是( )自我检测CD3.设A是△ABC的一个内角,且sin A+cos A= ,则这个三角形是( )
(A)锐角三角形 (B)钝角三角形
(C)等边三角形 (D)等腰直角三角形B4.化简: = .?答案:cos θ答案:-1题型一 已知角的一个三角函数值,求其他三角函数值课堂探究题型二 已知角的正切值,求同角三角函数式的值【例2】 设tan α=2,求下列各式的值:(2)2sin2α-3sin αcos α+5cos2α.方法技巧 化切求值的方法(2)对于asin2α+bsin αcos α+ccos2α的求值,可看成分母是1,利用1=
sin2α+cos2α进行代替后分子分母同时除以cos2α,得到关于tan α的式子,从而可以求值.(2)cos2x-sin xcos x.题型三 sin θ±cos θ与sin θcos θ之间的联系(2)求sin α-cos α的值.误区警示 在利用sin α±cos α与sin αcos α的关系求值时,一定注意判断它们的符号,否则就会出现漏解或错解.答案:-2题型四 三角函数式的化简与证明题后反思 利用同角三角函数关系式化简的方法
①化切为弦,减少函数名称,便于约分化简;②对含根号的,应先把被开方式化为完全平方,去掉根号,为防止出错,去掉根号后首先用绝对值号表示,然后考虑正负,以保证万无一失;③对含有高次的三角函数式,可借助于因式分解,或构造平方关系,以便于降幂化简.
