高中数学新人教A版必修4课件:第一章三角函数1.3三角函数的诱导公式:25张PPT
文档属性
| 名称 | 高中数学新人教A版必修4课件:第一章三角函数1.3三角函数的诱导公式:25张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-19 00:00:00 | ||
图片预览







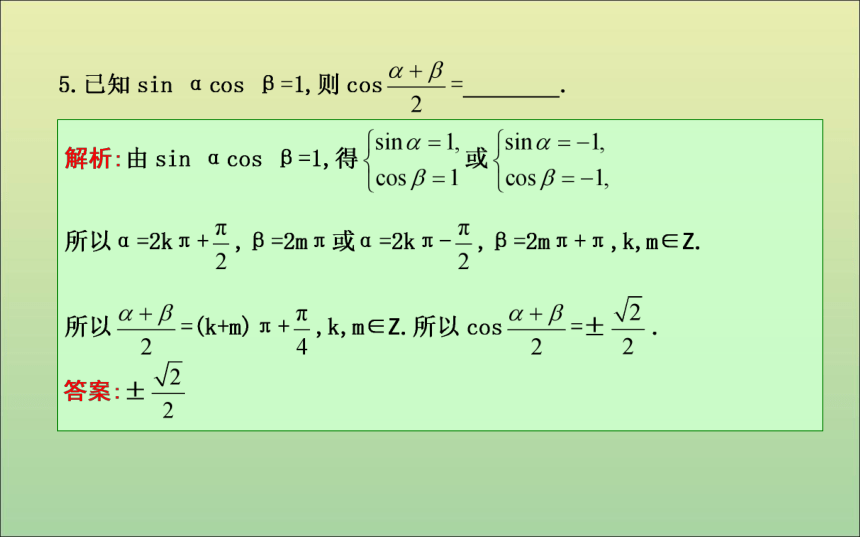
文档简介
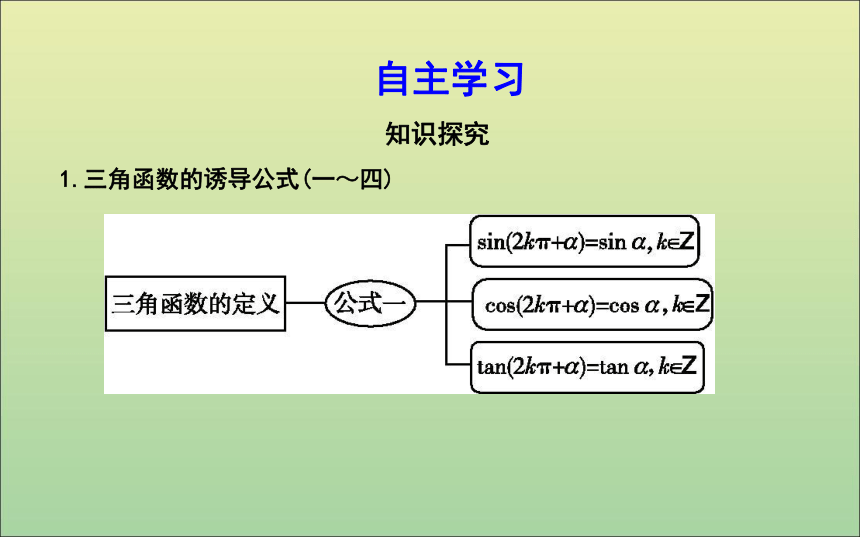
课件25张PPT。1.3 三角函数的诱导公式课标要求:1.理解诱导公式二、三、四的推导方法.2.准确记忆诱导公式二、三、四,会用以上公式解决三角函数化简、求值、证明问题.3.借助单位圆推导出诱导公式五、六.4.掌握六组诱导公式并能灵活运用.自主学习 1.三角函数的诱导公式(一~四) 知识探究这组诱导公式可以概括成:f(2kπ+α)=f(α),k∈Z,f可以表示sin,cos,
tan中任一种.(1)诱导公式二、三、四可以概括成:f(π+α)=±f(α),f(-α)=±f(α),
f(π-α)=±f(α),其中等号右边的“±”号只取其一,规律口诀是“函数名不变,符号看象限”.例如sin(π+α)=-sin α,就是正弦函数名不改变,α看成锐角,则π+α为第三象限角,第三象限角的正弦为负,故符号取“-”.
(2)上述诱导公式一至公式四都是为了化任意角成锐角α的,如果α为其他范围的角也都成立,这就是说,使用这些诱导公式,不必限定α为锐角,但是用口诀“函数名不变,符号看象限”时,都把α看成锐角记忆.
探究:公式一~四都叫做诱导公式,它们分别反映了2kπ+α(k∈Z),π+α,
-α,π-α的三角函数与α的三角函数之间的关系,你能概括一下这四组公式的共同特点和规律吗?
提示:2kπ+α(k∈Z),π+α,-α,π-α的三角函数值,等于α的同名函数值,前面加上一个把α看成锐角时原函数值的符号.简记为“函数名不变,符号看象限”.sin αcos αcos α-sin α自我检测DBA题型一 求任意角的三角函数值课堂探究答案:(3)②③答案:(1)C(2)sin2120°+cos 180°+tan 45°-cos2(-330°)+sin(-210°)=
.?题型二 已知三角函数值求相关角的三角函数值方法技巧 (1)解决条件求值问题的方法
①解决条件求值问题,首先要仔细观察条件与所求式的角、函数名称及有关运算之间的差异及联系.
②可以将已知式进行变形向所求式转化,或将所求式进行变形向已知式转化.
(2)角的转化方法
①对于负角的三角函数求值,可先利用诱导公式三,化为正角的三角函数.若转化之后的正角大于360°,再利用诱导公式一,化为0°到360°间的角的三角函数.
②当化成的角是90°到180°间的角时,再利用180°-α的诱导公式化为0°到90°间的角的三角函数.
③当化成的角是270°到360°间的角时,则利用360°-α及-α的诱导公式化为0°到90°间的角的三角函数.答案:(1)D 题型三 三角函数式的化简与证明答案:-1误区警示 (1)利用诱导公式一~四化简应注意的问题
①利用诱导公式主要是进行角的转化,从而达到统一角的目的;
②化简时函数名没有改变,但一定要注意函数的符号有没有改变;
③同时有切(正切)与弦(正弦、余弦)的式子化简,一般采用切化弦,有时也将弦化切;
(2)应用诱导公式化简三角函数式,要特别注意两点:一是公式选取要正确,二是符号的选取要正确,否则解题时易出错.
tan中任一种.(1)诱导公式二、三、四可以概括成:f(π+α)=±f(α),f(-α)=±f(α),
f(π-α)=±f(α),其中等号右边的“±”号只取其一,规律口诀是“函数名不变,符号看象限”.例如sin(π+α)=-sin α,就是正弦函数名不改变,α看成锐角,则π+α为第三象限角,第三象限角的正弦为负,故符号取“-”.
(2)上述诱导公式一至公式四都是为了化任意角成锐角α的,如果α为其他范围的角也都成立,这就是说,使用这些诱导公式,不必限定α为锐角,但是用口诀“函数名不变,符号看象限”时,都把α看成锐角记忆.
探究:公式一~四都叫做诱导公式,它们分别反映了2kπ+α(k∈Z),π+α,
-α,π-α的三角函数与α的三角函数之间的关系,你能概括一下这四组公式的共同特点和规律吗?
提示:2kπ+α(k∈Z),π+α,-α,π-α的三角函数值,等于α的同名函数值,前面加上一个把α看成锐角时原函数值的符号.简记为“函数名不变,符号看象限”.sin αcos αcos α-sin α自我检测DBA题型一 求任意角的三角函数值课堂探究答案:(3)②③答案:(1)C(2)sin2120°+cos 180°+tan 45°-cos2(-330°)+sin(-210°)=
.?题型二 已知三角函数值求相关角的三角函数值方法技巧 (1)解决条件求值问题的方法
①解决条件求值问题,首先要仔细观察条件与所求式的角、函数名称及有关运算之间的差异及联系.
②可以将已知式进行变形向所求式转化,或将所求式进行变形向已知式转化.
(2)角的转化方法
①对于负角的三角函数求值,可先利用诱导公式三,化为正角的三角函数.若转化之后的正角大于360°,再利用诱导公式一,化为0°到360°间的角的三角函数.
②当化成的角是90°到180°间的角时,再利用180°-α的诱导公式化为0°到90°间的角的三角函数.
③当化成的角是270°到360°间的角时,则利用360°-α及-α的诱导公式化为0°到90°间的角的三角函数.答案:(1)D 题型三 三角函数式的化简与证明答案:-1误区警示 (1)利用诱导公式一~四化简应注意的问题
①利用诱导公式主要是进行角的转化,从而达到统一角的目的;
②化简时函数名没有改变,但一定要注意函数的符号有没有改变;
③同时有切(正切)与弦(正弦、余弦)的式子化简,一般采用切化弦,有时也将弦化切;
(2)应用诱导公式化简三角函数式,要特别注意两点:一是公式选取要正确,二是符号的选取要正确,否则解题时易出错.
