高中数学新人教A版必修4课件:第一章三角函数1.4.1正弦函数、余弦函数的图象:23张PPT
文档属性
| 名称 | 高中数学新人教A版必修4课件:第一章三角函数1.4.1正弦函数、余弦函数的图象:23张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 709.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-19 10:32:22 | ||
图片预览







文档简介
课件23张PPT。1.4 三角函数的图象与性质
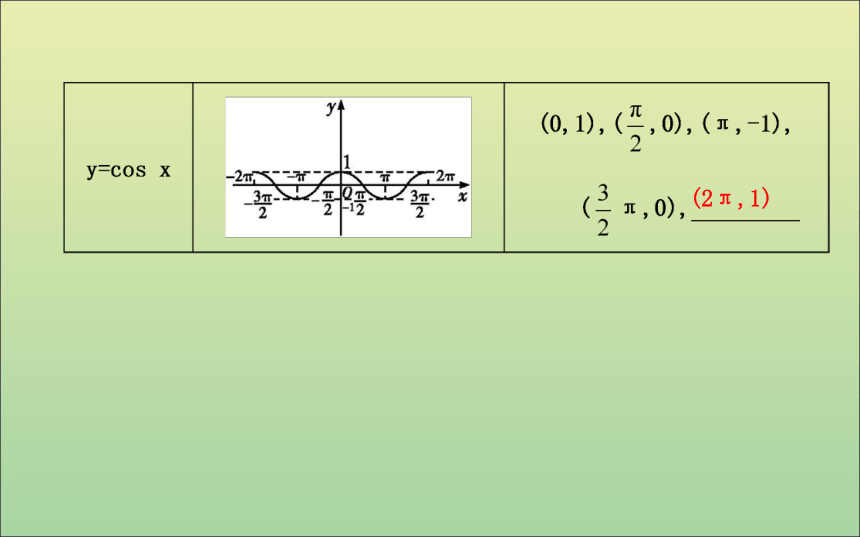
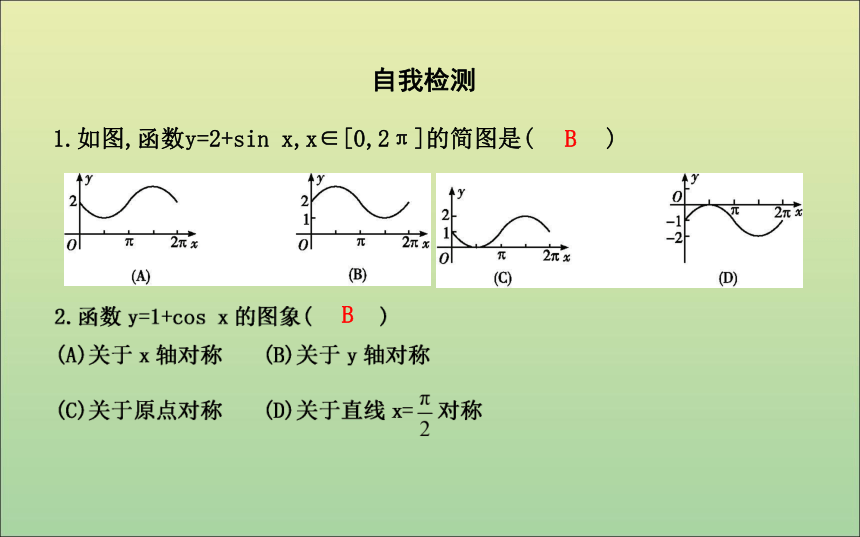
1.4.1 正弦函数、余弦函数的图象课标要求:1.了解正弦函数、余弦函数的图象.2.会用“五点法”画出正、余弦函数的图象.3.能利用正、余弦函数的图象解简单问题.自主学习 正弦函数、余弦函数的图象知识探究(2π,0)(2π,1)探究:用五点作图法作正弦函数、余弦函数的图象时如何确定五点?1.如图,函数y=2+sin x,x∈[0,2π]的简图是( )自我检测BBA4.用五点作图法作y=1-cos x,x∈[0,2π]的图象时,其中第二个关键点的坐标为 .?5.函数f(x)的定义域为[0,1],则f(cos x)的定义域是 .?题型一 利用“五点法”作简图课堂探究【例1】 用“五点法”作出函数y=1+2sin x,x∈[0,2π]的图象.即时训练1-1:(1)函数y=1-sin x,x∈[0,2π] 的大致图象是( )题型二 利用正、余弦函数图象解不等式方法技巧 用三角函数图象解三角不等式的方法
(1)作出相应的正弦函数或余弦函数在[0,2π]上的图象;
(2)写出适合不等式在区间[0,2π]上的解集;
(3)根据公式一写出定义域内的解集.题型三 正、余弦曲线与其他曲线的交点问题【例3】 判断方程sin x=lg x的解的个数.方法技巧 (1)确定方程解的个数问题,常借助函数图象用数形结合的方法求解;(2)三角函数的图象是研究函数的重要工具,通过图象可较简便地解决问题,这正是数形结合思想方法的应用.即时训练3-1:(1)方程x2-cos x=0的实数解的个数是 ;?解析:(1)在同一坐标系内画出y=x2与y=cos x的简图,易得交点个数是2个.答案:(1)2(2)已知函数f(x)=sin x+2|sin x|,x∈[0,2π],若直线y=k与其仅有两个不同的交点,则k的取值范围为 .?答案:(2)(1,3)
1.4.1 正弦函数、余弦函数的图象课标要求:1.了解正弦函数、余弦函数的图象.2.会用“五点法”画出正、余弦函数的图象.3.能利用正、余弦函数的图象解简单问题.自主学习 正弦函数、余弦函数的图象知识探究(2π,0)(2π,1)探究:用五点作图法作正弦函数、余弦函数的图象时如何确定五点?1.如图,函数y=2+sin x,x∈[0,2π]的简图是( )自我检测BBA4.用五点作图法作y=1-cos x,x∈[0,2π]的图象时,其中第二个关键点的坐标为 .?5.函数f(x)的定义域为[0,1],则f(cos x)的定义域是 .?题型一 利用“五点法”作简图课堂探究【例1】 用“五点法”作出函数y=1+2sin x,x∈[0,2π]的图象.即时训练1-1:(1)函数y=1-sin x,x∈[0,2π] 的大致图象是( )题型二 利用正、余弦函数图象解不等式方法技巧 用三角函数图象解三角不等式的方法
(1)作出相应的正弦函数或余弦函数在[0,2π]上的图象;
(2)写出适合不等式在区间[0,2π]上的解集;
(3)根据公式一写出定义域内的解集.题型三 正、余弦曲线与其他曲线的交点问题【例3】 判断方程sin x=lg x的解的个数.方法技巧 (1)确定方程解的个数问题,常借助函数图象用数形结合的方法求解;(2)三角函数的图象是研究函数的重要工具,通过图象可较简便地解决问题,这正是数形结合思想方法的应用.即时训练3-1:(1)方程x2-cos x=0的实数解的个数是 ;?解析:(1)在同一坐标系内画出y=x2与y=cos x的简图,易得交点个数是2个.答案:(1)2(2)已知函数f(x)=sin x+2|sin x|,x∈[0,2π],若直线y=k与其仅有两个不同的交点,则k的取值范围为 .?答案:(2)(1,3)
