高中数学新人教A版必修4课件:第一章三角函数1.4.2正弦函数、余弦函数的性质:31张PPT
文档属性
| 名称 | 高中数学新人教A版必修4课件:第一章三角函数1.4.2正弦函数、余弦函数的性质:31张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-19 00:00:00 | ||
图片预览









文档简介
课件31张PPT。1.4.2 正弦函数、余弦函数的性质课标要求:1.了解周期函数与最小正周期的意义.2.了解三角函数的周期性和奇偶性.3.会利用周期性定义和诱导公式求简单三角函数的周期.4.借助图象直观理解正、余弦函数在[0,2π]上的性质(单调性、最值、图象与x轴的交点等).5.能利用性质解决一些简单问题.1.函数的周期性
(1)对于函数f(x),如果存在一个 ,使得当x取定义域内的 值时,都有 ,那么函数f(x)就叫做周期函数,
叫做这个函数的周期.
(2)如果在周期函数f(x)的所有周期中存在一个 ,那么这个
就叫做f(x)的最小正周期.
(3)记f(x)=sin x,则由sin(2kπ+x)=sin x(k∈Z),得f(x+2kπ)=f(x)对于每一个非零常数2kπ(k∈Z)都成立,余弦函数同理也是这样,所以正弦函数、余弦函数都是周期函数, 都是它们的周期,最小正周期为 .自主学习 知识探究非零常数T每一个f(x+T)=f(x) 非零常数T最小的正数最小正数2kπ(k∈Z且k≠0)2π探究1:是不是所有的周期函数都有最小正周期?
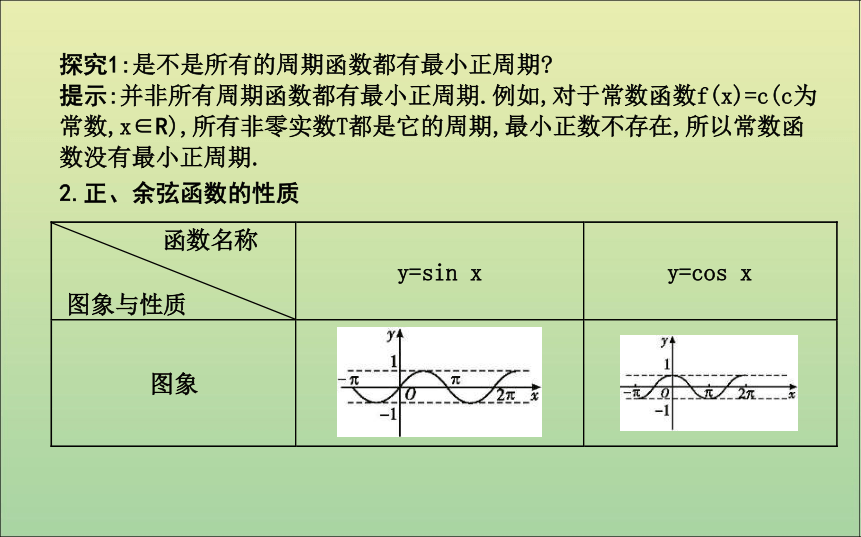
提示:并非所有周期函数都有最小正周期.例如,对于常数函数f(x)=c(c为常数,x∈R),所有非零实数T都是它的周期,最小正数不存在,所以常数函数没有最小正周期.
2.正、余弦函数的性质RR[-1,1]2π奇偶递增递减递增递减[-1,1]2π探究2:正弦函数(余弦函数)是不是定义域上的单调函数?
提示:正弦函数(余弦函数)在其定义域上不是单调函数.
探究3:正弦曲线(余弦曲线)的对称中心一定是正弦曲线(余弦曲线)与x轴的交点吗?
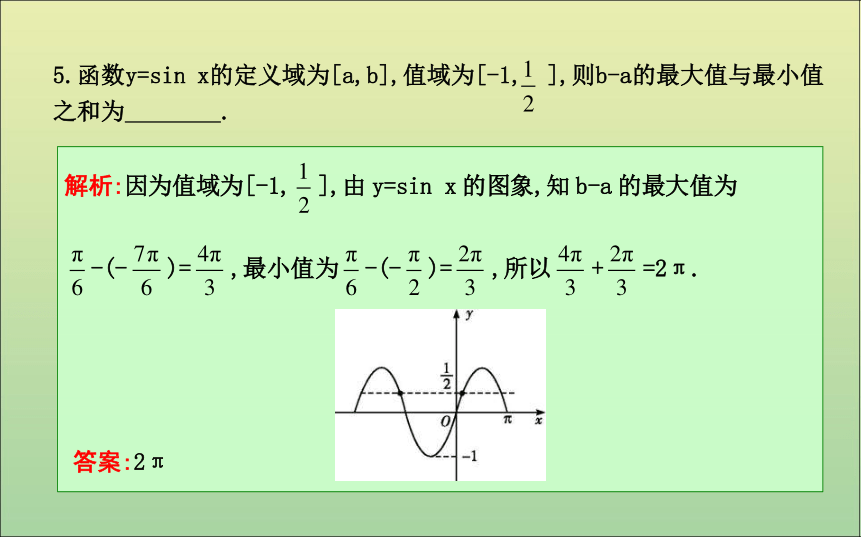
提示:是.2kπ(k∈Z)2kπ+π(k∈Z)自我检测DCD5.函数y=sin x的定义域为[a,b],值域为[-1, ],则b-a的最大值与最小值之和为 .?答案:2π题型一 正、余弦函数的周期性课堂探究【例1】 求下列三角函数的最小正周期:
(1)y=3sin x,x∈R;(2)y=cos 2x,x∈R;解:(1)因为3sin(x+2π)=3sin x,所以由周期函数的定义知,y=3sin x的最小正周期为2π.
(2)因为cos 2(x+π)=cos(2x+2π)=cos 2x,
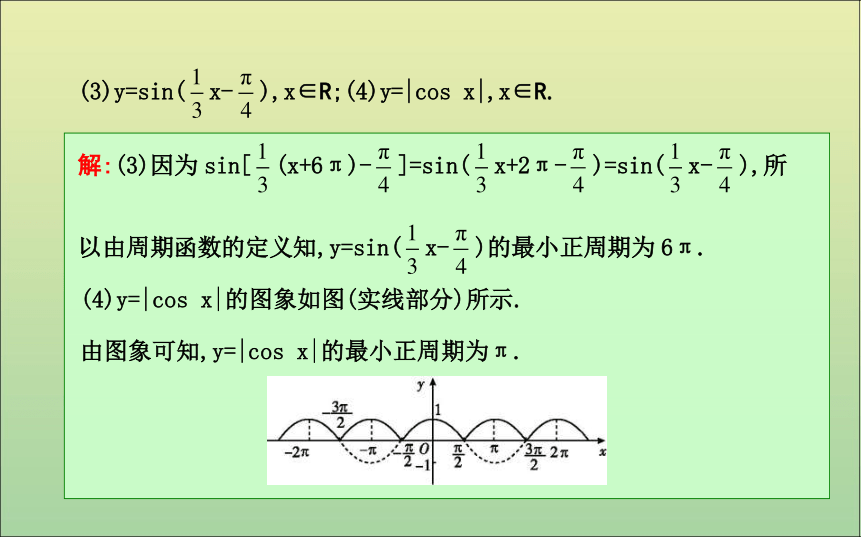
所以由周期函数的定义知,y=cos 2x的最小正周期为π.(4)y=|cos x|的图象如图(实线部分)所示.
由图象可知,y=|cos x|的最小正周期为π.(2)可以借助周期函数的定义或函数图象求最小正周期,有时需借助诱导公式化简后再求解.答案:(1)B(2)函数y=|sin 2x|(x∈R)的最小正周期为 .?题型二 正、余弦函数的奇偶性解:(3)显然x∈R,f(-x)=sin |-x|=sin |x|=f(x),
所以函数f(x)=sin |x|是偶函数.方法技巧 判断函数奇偶性的方法
(1)利用定义判断一个函数f(x)的奇偶性,要考虑两方面:①函数的定义域是否关于原点对称;②f(-x)与f(x)的关系;
(2)判断函数的奇偶性常用方法是:①定义法;②图象法.题型三 正、余弦函数的单调性题型四 正、余弦函数的值域与最值问题(2)y=cos2x-4cos x+5.解:(2)y=cos2x-4cos x+5,令t=cos x,
则-1≤t≤1.
y=t2-4t+5=(t-2)2+1,
当t=-1时,函数取得最大值10;
t=1时,函数取得最小值2,所以函数的值域为[2,10].即时训练4-1:(1)函数y=2cos2x+5sin x-4的值域为 .?答案:(1)[-9,1]答案:(2)1
(1)对于函数f(x),如果存在一个 ,使得当x取定义域内的 值时,都有 ,那么函数f(x)就叫做周期函数,
叫做这个函数的周期.
(2)如果在周期函数f(x)的所有周期中存在一个 ,那么这个
就叫做f(x)的最小正周期.
(3)记f(x)=sin x,则由sin(2kπ+x)=sin x(k∈Z),得f(x+2kπ)=f(x)对于每一个非零常数2kπ(k∈Z)都成立,余弦函数同理也是这样,所以正弦函数、余弦函数都是周期函数, 都是它们的周期,最小正周期为 .自主学习 知识探究非零常数T每一个f(x+T)=f(x) 非零常数T最小的正数最小正数2kπ(k∈Z且k≠0)2π探究1:是不是所有的周期函数都有最小正周期?
提示:并非所有周期函数都有最小正周期.例如,对于常数函数f(x)=c(c为常数,x∈R),所有非零实数T都是它的周期,最小正数不存在,所以常数函数没有最小正周期.
2.正、余弦函数的性质RR[-1,1]2π奇偶递增递减递增递减[-1,1]2π探究2:正弦函数(余弦函数)是不是定义域上的单调函数?
提示:正弦函数(余弦函数)在其定义域上不是单调函数.
探究3:正弦曲线(余弦曲线)的对称中心一定是正弦曲线(余弦曲线)与x轴的交点吗?
提示:是.2kπ(k∈Z)2kπ+π(k∈Z)自我检测DCD5.函数y=sin x的定义域为[a,b],值域为[-1, ],则b-a的最大值与最小值之和为 .?答案:2π题型一 正、余弦函数的周期性课堂探究【例1】 求下列三角函数的最小正周期:
(1)y=3sin x,x∈R;(2)y=cos 2x,x∈R;解:(1)因为3sin(x+2π)=3sin x,所以由周期函数的定义知,y=3sin x的最小正周期为2π.
(2)因为cos 2(x+π)=cos(2x+2π)=cos 2x,
所以由周期函数的定义知,y=cos 2x的最小正周期为π.(4)y=|cos x|的图象如图(实线部分)所示.
由图象可知,y=|cos x|的最小正周期为π.(2)可以借助周期函数的定义或函数图象求最小正周期,有时需借助诱导公式化简后再求解.答案:(1)B(2)函数y=|sin 2x|(x∈R)的最小正周期为 .?题型二 正、余弦函数的奇偶性解:(3)显然x∈R,f(-x)=sin |-x|=sin |x|=f(x),
所以函数f(x)=sin |x|是偶函数.方法技巧 判断函数奇偶性的方法
(1)利用定义判断一个函数f(x)的奇偶性,要考虑两方面:①函数的定义域是否关于原点对称;②f(-x)与f(x)的关系;
(2)判断函数的奇偶性常用方法是:①定义法;②图象法.题型三 正、余弦函数的单调性题型四 正、余弦函数的值域与最值问题(2)y=cos2x-4cos x+5.解:(2)y=cos2x-4cos x+5,令t=cos x,
则-1≤t≤1.
y=t2-4t+5=(t-2)2+1,
当t=-1时,函数取得最大值10;
t=1时,函数取得最小值2,所以函数的值域为[2,10].即时训练4-1:(1)函数y=2cos2x+5sin x-4的值域为 .?答案:(1)[-9,1]答案:(2)1
