高中数学新人教A版必修4课件:第一章三角函数1.6三角函数模型的简单应用:18张PPT
文档属性
| 名称 | 高中数学新人教A版必修4课件:第一章三角函数1.6三角函数模型的简单应用:18张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 394.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-19 00:00:00 | ||
图片预览





文档简介
课件18张PPT。1.6 三角函数模型的简单应用课标要求:1.会用三角函数解决一些简单实际问题.2.体会三角函数是描述周期变化现象的重要函数模型.自主学习 1.数学模型
数学模型就是把实际问题用数学语言抽象概括,再从数学角度来反映或近似地反映实际问题时,所得出的关于实际问题的数学描述.
2.解决三角函数应用问题的一般步骤
(1)审题
阅读、理解用文字语言表述的实际问题的类型、思想内涵、问题的实质,初步预测所属数学模型.
(2)建模
将题中的非数学语言转化为数学语言,然后根据题意,设出变量,画出散点图,列出数量关系——建立三角函数模型.知识探究(3)解模
运用三角函数的有关公式进行推理、运算,使问题得到解决.
(4)还原评价
对解出的结果要代入原问题中进行检验、评价.
探究:怎样处理搜集到的数据?
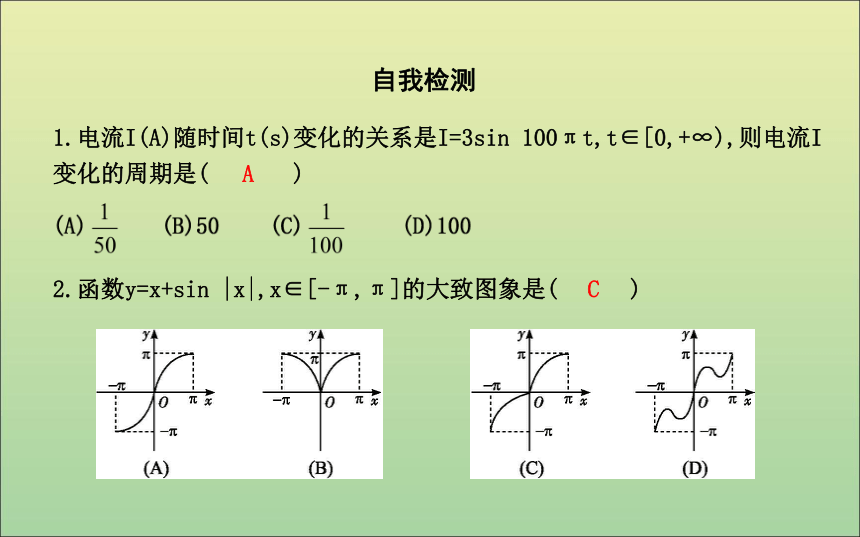
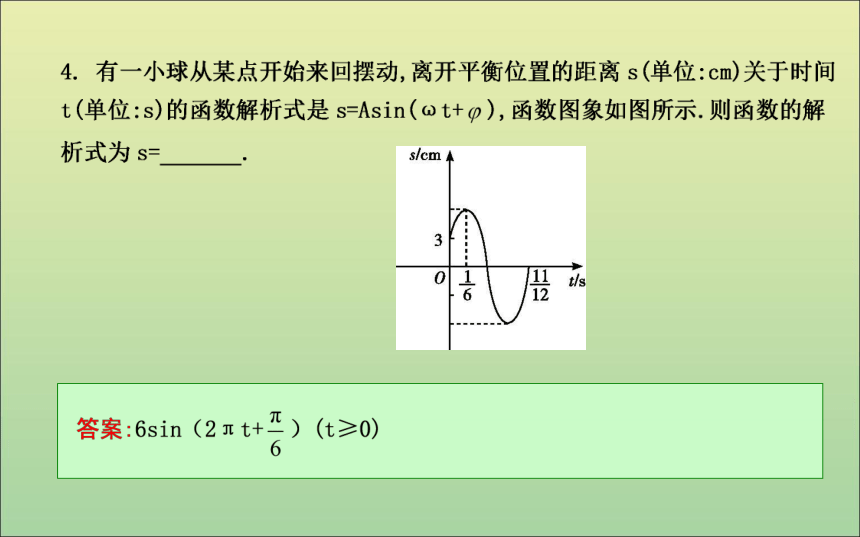
提示:画出图,分析数据的变化趋势,确定合适的函数模型.1.电流I(A)随时间t(s)变化的关系是I=3sin 100πt,t∈[0,+∞),则电流I变化的周期是( )自我检测A2.函数y=x+sin |x|,x∈[-π,π]的大致图象是( )CC(A)5 (B)6 (C)8 (D)10答案:±2题型一 根据函数图象研究实际问题课堂探究误区警示 利用待定系数法求出函数解析式,然后解决实际问题,求解时注意各变量的取值范围,为此,要在解析式后边注明函数的定义域.题型二 根据收集的数据研究函数问题【例2】 表中给出了在24小时期间某人的体温的变化(从夜间零点开始计时).(1)选用一个三角函数来近似描述体温与时间之间的关系;(2)画出(1)中所选函数的图象.解:(2)函数图象如图所示.方法技巧 建立三角函数模型解决实际问题的步骤:
(1)根据已知数据画散点图.
(2)由散点图确定函数模型.
(3)待定系数法求各参数,确定函数模型的表达式.
(4)注明定义域.即时训练2-1:某港口水深y(m)是时间t(0≤t≤24,单位:h)的函数,记作y=f(t),下面是某日水深的数据.经长期观察,y=f(t)的曲线可近似地看成是函数y=Asinωt+b的图象.解:(1)由已知数据,描出曲线如图.(1)试根据以上数据,求出函数y=f(t)的近似解析式;(2)一般情况下,船舶航行时,船底高出海底的距离为5 m或5 m以上时认为是安全的(船舶停靠时,船底只需不碰海底即可),某船吃水深度(船底离水面的距离)为6.5 m,如果该船希望在同一天内安全进出港,那么它至多能在港内停留多长时间?(忽略进出港所需的时间)
数学模型就是把实际问题用数学语言抽象概括,再从数学角度来反映或近似地反映实际问题时,所得出的关于实际问题的数学描述.
2.解决三角函数应用问题的一般步骤
(1)审题
阅读、理解用文字语言表述的实际问题的类型、思想内涵、问题的实质,初步预测所属数学模型.
(2)建模
将题中的非数学语言转化为数学语言,然后根据题意,设出变量,画出散点图,列出数量关系——建立三角函数模型.知识探究(3)解模
运用三角函数的有关公式进行推理、运算,使问题得到解决.
(4)还原评价
对解出的结果要代入原问题中进行检验、评价.
探究:怎样处理搜集到的数据?
提示:画出图,分析数据的变化趋势,确定合适的函数模型.1.电流I(A)随时间t(s)变化的关系是I=3sin 100πt,t∈[0,+∞),则电流I变化的周期是( )自我检测A2.函数y=x+sin |x|,x∈[-π,π]的大致图象是( )CC(A)5 (B)6 (C)8 (D)10答案:±2题型一 根据函数图象研究实际问题课堂探究误区警示 利用待定系数法求出函数解析式,然后解决实际问题,求解时注意各变量的取值范围,为此,要在解析式后边注明函数的定义域.题型二 根据收集的数据研究函数问题【例2】 表中给出了在24小时期间某人的体温的变化(从夜间零点开始计时).(1)选用一个三角函数来近似描述体温与时间之间的关系;(2)画出(1)中所选函数的图象.解:(2)函数图象如图所示.方法技巧 建立三角函数模型解决实际问题的步骤:
(1)根据已知数据画散点图.
(2)由散点图确定函数模型.
(3)待定系数法求各参数,确定函数模型的表达式.
(4)注明定义域.即时训练2-1:某港口水深y(m)是时间t(0≤t≤24,单位:h)的函数,记作y=f(t),下面是某日水深的数据.经长期观察,y=f(t)的曲线可近似地看成是函数y=Asinωt+b的图象.解:(1)由已知数据,描出曲线如图.(1)试根据以上数据,求出函数y=f(t)的近似解析式;(2)一般情况下,船舶航行时,船底高出海底的距离为5 m或5 m以上时认为是安全的(船舶停靠时,船底只需不碰海底即可),某船吃水深度(船底离水面的距离)为6.5 m,如果该船希望在同一天内安全进出港,那么它至多能在港内停留多长时间?(忽略进出港所需的时间)
