人教版高中数学必修二知识讲解,巩固练习(教学资料,补习资料):第01章 章末检测
文档属性
| 名称 | 人教版高中数学必修二知识讲解,巩固练习(教学资料,补习资料):第01章 章末检测 |  | |
| 格式 | zip | ||
| 文件大小 | 641.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-19 10:44:02 | ||
图片预览

文档简介
空间几何体
章末检测
选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.
1.下列各组几何体中,都是多面体的一组是
A.三棱柱、四棱台、球、圆锥
B.三棱柱、四棱台、正方体、圆台
C.三棱柱、四棱台、正方体、六棱锥
D.圆锥、圆台、球、半球
2.一个晴朗的上午,小明拿着一块长方形的木板在阳光下做投影实验,长方形的木板在地面上形成的投影不可能是
A. B.
C. D.
3.已知三棱柱ABC-A1B1C1,如图所示,则其三视图为
A. B.
C. D.
4.已知长方体的三条棱长分别是3,4,x,且它的8个顶点都在同一个球面上,这个球的表面积为125π,则x的值为
A.5 B.6
C.8 D.10
5.一个四棱锥的三视图如图所示,那么对于这个四棱锥,下列说法中正确的是
A.最长棱的棱长为
B.最长棱的棱长为
C.侧面四个三角形中有且仅有一个是正三角形
D.侧面四个三角形都是直角三角形
6.上、下底面面积分别为36π和49π,母线长为5的圆台,两底面间的距离为
A.4 B.
C. D.
7.利用斜二测画法画平面内一个△ABC的直观图得到的图形是,那么的面积与△ABC的面积的比是
A. B.
C. D.
8.一简单几何体的三视图如下图所示,则该几何体最大的面的面积等于
A. B.
C. D.
9.某几何体的三视图如图所示,其中三个圆的半径都为1,三个小扇形都是个圆,则该几何体的表面积为
A. B.
C. D.
10.在四面体中,,则该四面体外接球的表面积是
A. B.
C. D.
11.《九章算术》中将底面是直角三角形的直三棱柱称之为“堑堵”.一块“堑堵”型石材表示的三视图如图所示.将该石材切削、打磨,加工成若干个相同的球,并使每个球的体积最大,则所剩余材料的体积为
A. B.
C. D.
12.正三棱锥P—ABC中,,,AB的中点为M,一小蜜蜂沿锥体侧面由M 爬到C点,最短路程是
A. B.
C. D.
二、填空题:请将答案填在题中横线上.
13.半径为4的球的表面积为________.
14.若一个圆锥的轴截面是等边三角形,其面积为,则这个圆锥的全面积等于__________.
15.一个几何体的三视图如图所示,其中正视图是正三角形,则几何体的外接球的表面积为________.
16.若某几何体的三视图(单位:cm)如图所示,则此几何体的体积是___________.
(,其中S′、S分别为上、下底面面积,h为高)
三、解答题:解答应写出文字说明、证明过程或演算步骤.
17.某建筑由相同的若干房间组成,该楼房的三视图如图所示,问:
(1)该楼房有几层?从前往后最多要经过几个房间?
(2)最高一层的房间在什么位置?请画出此楼房的大致形状.
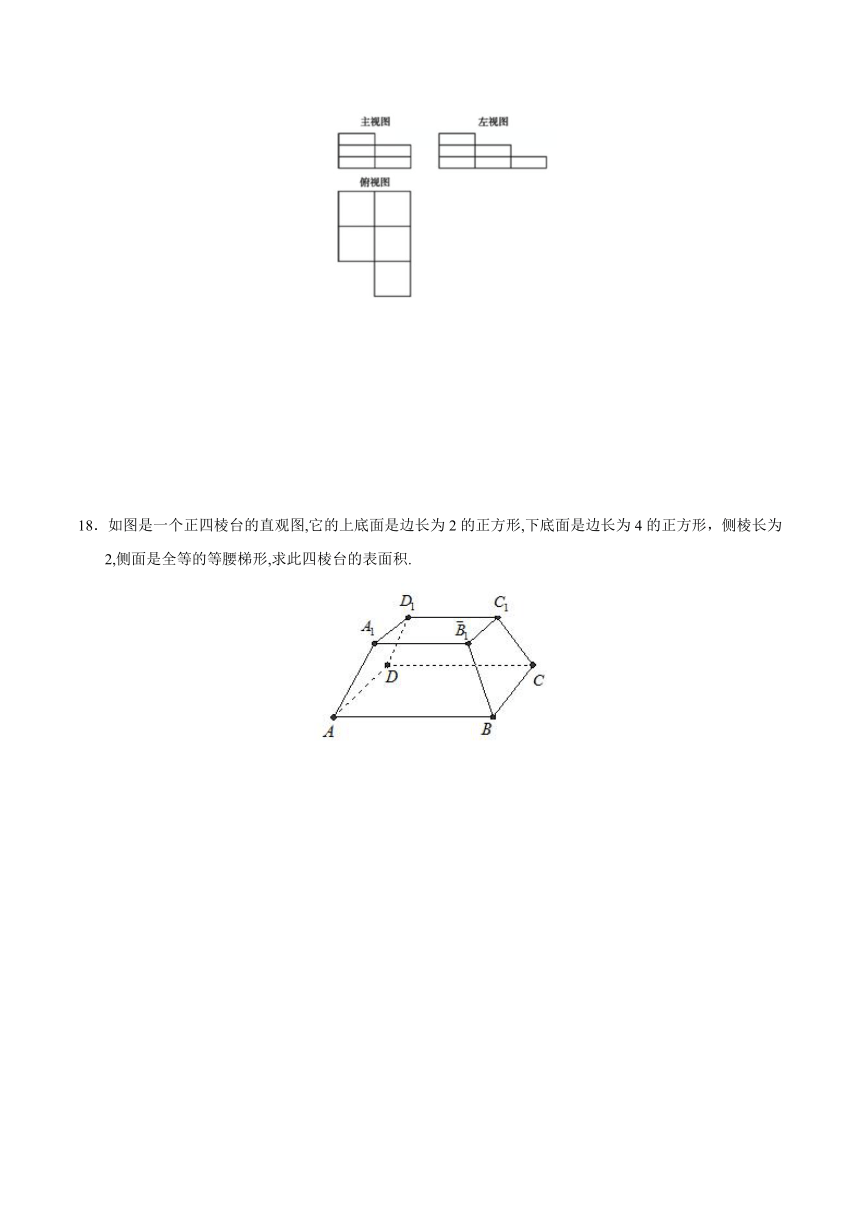
18.如图是一个正四棱台的直观图,它的上底面是边长为2的正方形,下底面是边长为4的正方形,侧棱长为2,侧面是全等的等腰梯形,求此四棱台的表面积.
19.设下图是某几何体的三视图,求该几何体的体积和表面积.
20.如图所示,在边长为的正方形ABCD中,以A为圆心画一个扇形,以O为圆心画一个圆,M,N,K为切点,以扇形为圆锥的侧面,以圆O为圆锥的底面,围成一个圆锥,求这个圆锥的表面积和体积.
21.某几何体的正视图和侧视图如图所示,它的俯视图的直观图是,其中
(1)画出该几何体的直观图;
(2)求该几何体的体积和表面积.
22.底面半径为2,高为的圆锥有一个内接的正四棱柱(底面是正方形,侧棱与底面垂直的四棱柱).
(1)设正四棱柱的底面边长为,试将棱柱的高表示成的函数;
(2)当取何值时,此正四棱柱的表面积最大,并求出最大值.
参考答案
1
2
3
4
5
6
7
8
9
10
11
12
C
A
A
D
D
D
A
B
A
D
C
A
1.【答案】C
2.【答案】A
【解析】由物体同一时刻物高与影长成比例,且矩形对边相等,梯形两底不相等,得到投影不可能是等腰梯形.故选A.
3.【答案】A
【解析】其正视图为矩形,侧视图为三角形,俯视图中棱CC1可见,为实线,只有A符合.
本题选择A选项.
4.【答案】D?
【解析】设球的半径为r,则4πr2=125π,∴r2=.又32+42+x2=(2r)2,∴9+16+x2=125,∴x2=100,即x=10.
5.【答案】D
【解析】由三视图可知该几何体是一个底面为直角梯形,其中一条侧棱垂直于底面的四棱锥,如图所示:
根据三视图中的数据可知最长棱的棱长为,所以选项A和选项B都错误;
根据三视图可知侧面四个三角形都是直角三角形,所以选项D正确.
故选D.
6.【答案】D
【解析】由题意,得圆台上、下底面半径分别为6和7,在圆台的轴截面等腰梯形中,易求得两底面距离.
7.【答案】A
【名师点睛】本题考查了平面图形的斜二测画法,首先掌握斜二测画法的原则,平行于轴或是在轴上的长度不变,平行于轴或是在轴上的长度变为原来的一半,然后会还原为实际图形,直观图与实际图形的面积比值是.
8.【答案】B
【解析】由三视图可知该几何体是底面为等腰直角三角形,一条侧棱垂直于底面的三棱锥,如下图所示.
其中正方体的棱长为,,所以面积最大的面为侧面及侧面,其面积为,故选B.
9.【答案】A
【解析】本题主要考查空间几何体的三视图、表面积与体积,考查了空间想象能力.由三视图可知,该几何体是半径为1的球的右下方截下球,因此该几何体的表面积S=.
10.【答案】D
11.【答案】C
【解析】如图所示,作三棱柱底面的内切圆,设内切接圆的半径为,
则,,
∴,故,
又三棱柱的高为,故共有个球,该三棱柱的体积等于,
剩余材料的体积为,故选C.
【名师点睛】本题利用空间几何体的三视图重点考查学生的空间想象能力和抽象思维能力,属于难题.三视图问题是考查学生空间想象能力最常见的题型,也是高考热点.观察三视图并将其“翻译”成直观图是解题的关键,不但要注意三视图的三要素“高平齐,长对正,宽相等”,还要特别注意实线与虚线以及相同图形的不同位置对几何体直观图的影响,对简单组合体三视图问题,先看俯视图确定底面的形状,根据正视图和侧视图,确定组合体的形状.
12.【答案】A
13.【答案】64
【解析】本题考查球的表面积.由题意得球的表面积.
14.【答案】
【解析】设圆锥的底面圆的直径为a,则
所以圆锥的全面积=故答案为.
【名师点睛】(1)本题主要考查圆锥及其全面积的计算,意在考查学生对这些基础知识的掌握能力.
(2)S扇形==,其中代表弧长,代表圆的半径,代表圆心角的角度数.
15.【答案】
16.【答案】
【解析】三视图复原的几何体上部是圆台,下部是半球,
半球的体积:,
圆台的体积:,
几何体的体积为.
故答案为.
【名师点睛】(1)解决组合体问题关键是分清该几何体是由哪些简单的几何体组成的以及这些简单的几何体的组合情况;
(2)由三视图求几何体的面积、体积,关键是由三视图还原几何体,同时还需掌握求体积的常用技巧如:割补法和等价转化法.
(3)解本题时,由题意可知,几何体上部是圆台,下部是半球,根据三视图数据,求出几何体的体积即可.
17.【答案】(1);(2)左侧的最后一排,如图(答案不唯一).
【解析】(1)由主视图和左视图可以知道,该楼房有3层;
由俯视图知道,从前往后最多要经过3个房间.
(2)从主视图和左视图可以知道,最高一层的房间在左侧的最后一排的房间.
楼房大致形状如图所示(不唯一,画出其他符合三视图的楼房也正确).
18.【答案】.
19.【答案】体积为,表面积为.
【解析】该几何体是由一个球与一个长方体组成的组合体,球的直径为,长方体的底面是边长为的正方形,高为,
故所求体积为,
表面积为.
20.【答案】,.
【解析】设圆锥的母线长为l,底面半径为r,高为h,
由已知条件得,解得.
∴
又,所以.
21.【答案】(1)见解析;(2)见解析.
【解析】(1)由题意结合俯视图的直观图可知三棱锥的底面为边长为4的等边三角形,且侧棱是三棱锥P?ABC的高.
22.【答案】(1);(2)当时,表面积最大,最大值为.
【解析】(1)如图,由题意知,△∽△,所以可得,
又,
所以得,整理得.
(2)正四棱柱的表面积,因为,所以当时,表面积最大,最大值为.
