人教版高中数学必修二知识讲解,巩固练习(教学资料,补习资料):第02章 章末检测
文档属性
| 名称 | 人教版高中数学必修二知识讲解,巩固练习(教学资料,补习资料):第02章 章末检测 |

|
|
| 格式 | zip | ||
| 文件大小 | 268.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-19 00:00:00 | ||
图片预览


文档简介
第二章 点、直线、平面之间的位置关系
章末检测
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.
1.下列命题正确的是
A.经过三点确定一个平面
B.经过一条直线和一个点确定一个平面
C.四边形确定一个平面
D.两两相交且不共点的三条直线确定一个平面
2.如图,A–BCDE是一个四棱锥,AB⊥平面BCDE,且四边形BCDE为矩形,则图中互相垂直的平面共有
A.4组 B.5组
C.6组 D.7组
3.若a、b表示直线,α表示平面,下列命题中正确的个数为
①a⊥α,b∥α?a⊥b;②a⊥α,a⊥b?b∥α;③a∥α,a⊥b?b⊥α.
A.0 B.1
C.2 D.3
4.正方体ABCD–A1B1C1D1中,直线BC1与AC
A.异面且垂直 B.异面但不垂直
C.相交且垂直 D.相交但不垂直
5.下列命题正确的是
A.一直线与平面平行,则它与平面内任一直线平行
B.一直线与平面平行,则平面内有且只有一条直线与已知直线平行
C.一直线与平面平行,则平面内有无数直线与已知直线平行,它们在平面内彼此平行
D.一直线与平面平行,则平面内任意直线都与已知直线异面
6.如果空间四点A、B、C、D不共面,那么下列判断中正确的是
A.A、B、C、D四点中必有三点共线 B.A、B、C、D四点中不存在三点共线
C.直线AB与CD相交 D.直线AB与CD平行
7.两等角的一组对应边平行,则
A.另一组对应边平行 B.另一组对应边不平行
C.另一组对应边也不可能垂直 D.以上都不对
8.设m、n是两条不同的直线,α、β、γ是三个不同的平面,给出下列四个命题:
①若α∥β,α∥γ,则β∥γ;②若α⊥β,m∥α,则m⊥β;
③若m⊥α,m∥β,则α⊥β;④若m∥n,n?α,则m∥α.
其中正确命题的序号是
A.①③ B.①④ C.②③ D.②④
9.已知α、β是两个不同平面,m、n是两不同直线,下列命题中的假命题是
A.若m∥n,m⊥α,则n⊥α B.若m∥α,α∩β=n,则m∥n
C.若m⊥α,m⊥β,则α∥β D.若m⊥α,m?β,则α⊥β
10.下列命题中错误的是
A.如果α⊥β,那么α内一定存在直线平行于平面β
B.如果α⊥β,那么α内所有直线都垂直于平面β
C.如果平面α不垂直平面β,那么α内一定不存在直线垂直于平面β
D.如果α⊥γ,β⊥γ,α∩β=l,那么l⊥γ
11.如图,在三棱锥A–BCD中,AB⊥平面BCD,∠ACB=45°,∠ADB=30°,∠BCD=90°,CD=40,则AB=
A.10 B.20 C.10 D.20
12.下列命题,能得出直线m与平面α平行的是
A.直线m与平面α内所有直线平行 B.直线m与平面α内无数条直线平行
C.直线m与平面α没有公共点 D.直线m与平面α内的一条直线平行
二、填空题:请将答案填在题中横线上.
13.如果两条直线a和b没有公共点,那么a与b的位置关系是__________.
14.若A∈α,B?α,A∈l,B∈l,那么直线l与平面α有__________个公共点.
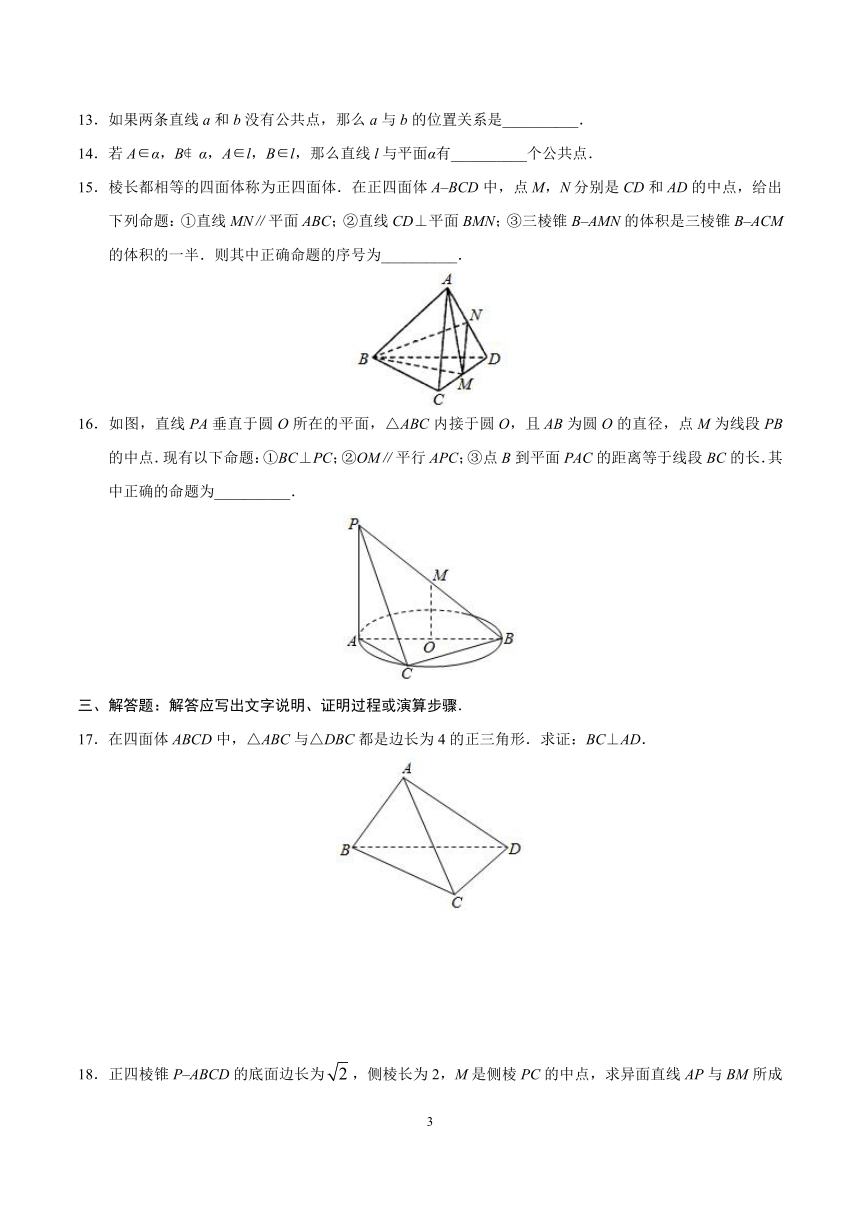
15.棱长都相等的四面体称为正四面体.在正四面体A–BCD中,点M,N分别是CD和AD的中点,给出下列命题:①直线MN∥平面ABC;②直线CD⊥平面BMN;③三棱锥B–AMN的体积是三棱锥B–ACM的体积的一半.则其中正确命题的序号为__________.
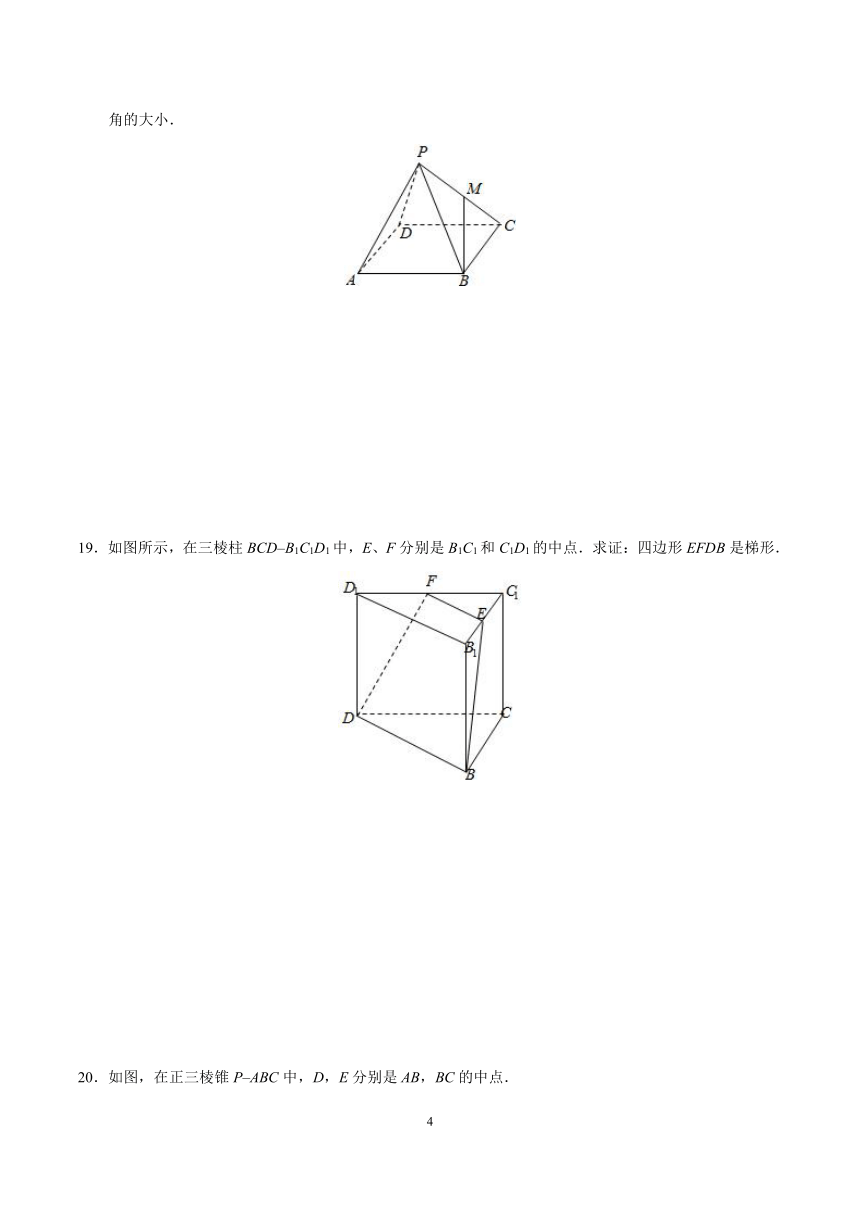
16.如图,直线PA垂直于圆O所在的平面,△ABC内接于圆O,且AB为圆O的直径,点M为线段PB的中点.现有以下命题:①BC⊥PC;②OM∥平行APC;③点B到平面PAC的距离等于线段BC的长.其中正确的命题为__________.
三、解答题:解答应写出文字说明、证明过程或演算步骤.
17.在四面体ABCD中,△ABC与△DBC都是边长为4的正三角形.求证:BC⊥AD.
18.正四棱锥P–ABCD的底面边长为,侧棱长为2,M是侧棱PC的中点,求异面直线AP与BM所成角的大小.
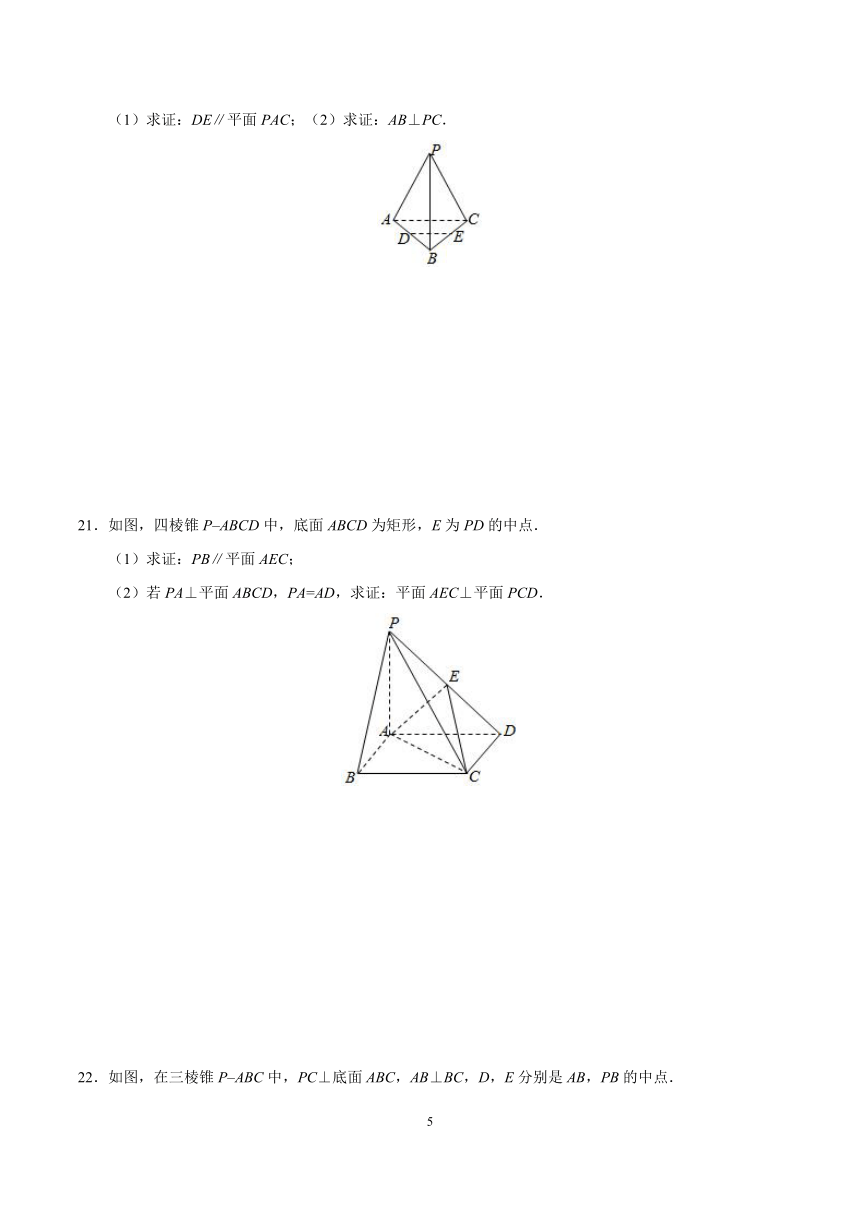
19.如图所示,在三棱柱BCD–B1C1D1中,E、F分别是B1C1和C1D1的中点.求证:四边形EFDB是梯形.
20.如图,在正三棱锥P–ABC中,D,E分别是AB,BC的中点.
(1)求证:DE∥平面PAC;(2)求证:AB⊥PC.
21.如图,四棱锥P–ABCD中,底面ABCD为矩形,E为PD的中点.
(1)求证:PB∥平面AEC;
(2)若PA⊥平面ABCD,PA=AD,求证:平面AEC⊥平面PCD.
22.如图,在三棱锥P–ABC中,PC⊥底面ABC,AB⊥BC,D,E分别是AB,PB的中点.
(1)求证:DE∥PA;(2)求证:DE∥平面PAC;(3)求证:AB⊥PB.
参考答案
1
2
3
4
5
6
7
8
9
10
11
12
D
C
B
B
C
B
D
A
B
B
D
C
1.【答案】D
2.【答案】C
【解析】因为AB⊥平面BCDE,所以平面ABC⊥平面BCDE,平面ABD⊥平面BCDE,平面ABE⊥平面BCDE,又因为四边形BCDE为矩形,所以BC⊥平面ABE?平面ABC⊥平面ABE,同理可得平面ACD⊥平面ABC.平面ADE⊥平面ABE,故图中互相垂直的平面共有6组.故选C.
3.【答案】B
【解析】①a⊥α,b∥α,则a与b相交垂直或异面垂直,故a⊥b,故①正确;②a⊥α,a⊥b,则b∥α或b?α,故②错误;③a∥α,a⊥b,则b与α相交、平行或b?α,故③错误.故选B.
4.【答案】B
【解析】如图,正方体ABCD–A1B1C1D1中,直线BC1与AC是异面直线.将BC1平移至AD1处,∠D1AC就是所求的角,又△AD1C为正三角形.∴∠D1AC=60°.故异面直线AC与BC1所成的角的大小为60°.故选B.
5.【答案】C
6.【答案】B
【解析】空间四点A、B、C、D不共面,则四点所处的位置如四面体的四个顶点.可得只有答案B正确.故选B.
7.【答案】D
【解析】两个等角的一组对边平行,另外一组边可以具有各种位置关系,并且不能确定是哪一种关系,故选D.
8.【答案】A
【解析】对于①,若α∥β,α∥γ根据面面平行的性质容易得到β∥γ;故①正确;对于②,若α⊥β,m∥α,m与β的关系不确定;故②错误;对于③,若m⊥α,m∥β,可以在β找到一条直线n与m平行,所以n⊥α,故α⊥β;故③正确;对于④,若m∥n,n?α,那么m与α的位置关系为m∥α或者m?α;故④错误.故选A.
9.【答案】B
【解析】若m∥n,m⊥α,由线面垂直的第二判定定理,我们可得n⊥α,故A正确;若m∥α,α∩β=n,m与n可能平行也可能异面,故B错误;若m⊥α,m⊥β,则根据垂直于同一直线的两个平面平行,则α∥β,故C正确;若m⊥α,m?β,则根据线面垂直的判定定理,则α⊥β,故D正确.故选B.
10.【答案】B
【解析】如果α⊥β,则α内与两平面的交线平行的直线都平行于面β,故可推断出A命题正确.B选项中α内与两平面的交线平行的直线都平行于面β,故B命题错误.C根据平面与平面垂直的判定定理可知C命题正确.D根据两个平面垂直的性质推断出D命题正确.故选B.
11.【答案】D
12.【答案】C
【解析】A命题本身说法错误.B当直线m在平面α内,m与α不平行.C项能推出m与α平行.D项,当直线m在平面α内满足,m与α不平行.故选C.
13.【答案】平行或异面
【解析】空间中两条直线的位置关系有三种:相交,有且只有一个公共点;平行,没有公共点;异面,没有公共点.由此可知,如果两条直线a和b没有公共点,那么a与b的位置关系是平行或异面.故答案为平行或异面.
14.【答案】1
【解析】∵A∈α,A∈l,直线l与平面α有公共点A,∴直线l?平面α或直线l∩平面α=A,下面用反证法证明直线l不可能在平面α内:假设直线l?平面α,因为B∈l,所以B∈α,这与已知条件“B?α”矛盾,故“直线l?平面α”不能成立,∴直线l∩平面α=A,直线l与平面α有唯一公共点,故答案为1.
15.【答案】①、③
【解析】∵点M,N分别是CD和AD的中点,∴MN∥AC,又由MN?平面ABC,AC?平面ABC,
∴①直线MN∥平面ABC正确;由于∠ACD=60°,∴AC与CD不垂直,则NM与CD也不垂直,故直线CD与平面BMN也不垂直,∴②直线CD⊥平面BMN错误;∵三棱锥B–AMN与三棱锥B–ACM的高相等.△AMN与△ACM高相等且底边之比为1:2,∴③三棱锥B–AMN的体积是三棱锥B–ACM的体积的一半正确.故答案为①、③.
16.【答案】①②③
17.【答案】证明详见解析.
【解析】取BC中点O,连接AO,DO.
∵△ABC,△BCD都是边长为4的正三角形,
∴AO⊥BC,DO⊥BC,且AO∩DO=O,∴BC⊥平面AOD.
又AD?平面AOD,∴BC⊥AD.
18.【答案】45°.
【解析】连接AC,BD交于O点,连接MO.
由MO∥PA知,∠OMB即为PA与BM所成的角.
∵P–ABCD是正四棱锥,
∴PO⊥平面ABCD.又AC⊥BD,∴PA⊥BD,MO⊥BD,
Rt△OMB中,OM⊥OB,OM==1,BO=,∴∠OMB=45°,
∴异面直线PA与BM所成角的为45°.
19.【答案】证明详见解析.
【解析】∵E、F分别是B1C1和C1D1的中点,
∴在△C1B1D1中,C1E=EB1,C1F=FD1,∴EF∥B1D1,且EF=B1D1,
又∵B1BD1D,且B1B=D1D,∴四边形BB1D1D是平行四边形,∴B1D1∥BD,
∴EF∥BD,EF=BD,∴四边形EFDB是梯形.
20.【答案】(1)证明详见解析.(2)证明详见解析.
21.【答案】(1)证明详见解析.(2)证明详见解析.
【解析】(1)连接BD交AC于O点,连接EO,
∵O为BD中点,E为PD中点,∴EO∥PB,
又EO?平面AEC,PB?平面AEC,∴PB∥平面AEC.
(2)∵PA⊥平面ABCD,CD?平面ABCD,∴PA⊥CD,
又AD⊥CD,且AD∩PA=A,∴CD⊥平面PAD.
又AE?平面PAD,∴CD⊥AE.
∵PA=AD,E为PD中点,∴AE⊥PD.
又CD∩PD=D,∴AE⊥平面PDC,
又AE?平面PAD,∴平面PDC⊥平面AEC.
22.【答案】(1)证明详见解析.(2)证明详见解析.(3)证明详见解析.
