高中数学新人教A版必修5课件:第三章不等式3.2一元二次不等式及其解法第二课时一元二次不等式及其解法习题课(27张)
文档属性
| 名称 | 高中数学新人教A版必修5课件:第三章不等式3.2一元二次不等式及其解法第二课时一元二次不等式及其解法习题课(27张) |  | |
| 格式 | zip | ||
| 文件大小 | 453.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-20 14:58:12 | ||
图片预览








文档简介
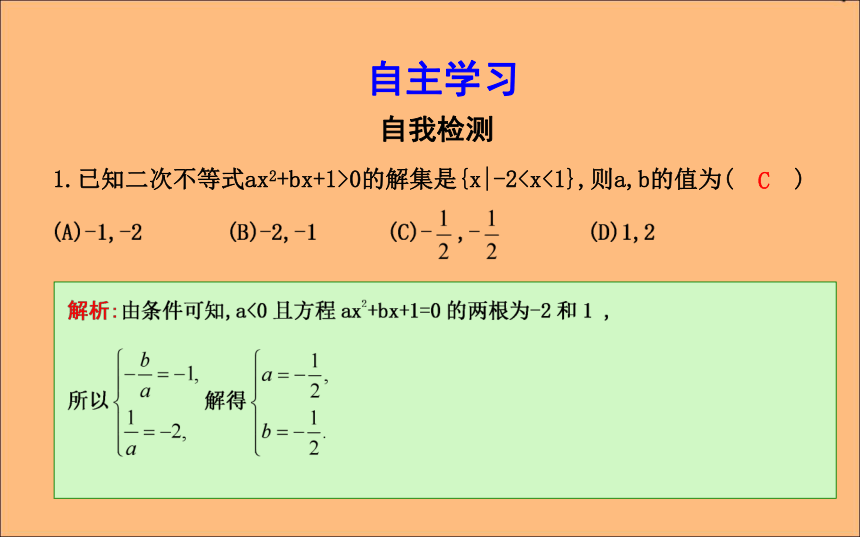
课件27张PPT。第二课时 一元二次不等式及其解法习题课课标要求:1.在掌握一元二次不等式解法的基础上,能够根据一元二次不等式的解集,确定不等式中参数的值.2.能够求解与一元二次不等式相关的不等式恒成立问题.3.能够从实际生活和生产中抽象出一元二次不等式的模型,并加以解决.自主学习1.已知二次不等式ax2+bx+1>0的解集是{x|-2(A)[-2,2]
(B)(-2,2)
(C)(-∞,-2]∪[2,+∞)
(D)(-∞,-2)∪(2,+∞)A解析:由Δ≤0知a2-4≤0,所以-2≤a≤2.3.已知集合P={0,m},Q={x|2x2-5x<0,x∈Z},若P∩Q≠ ,则m等于( )D 解析:因为Q={x|0所以m=1或2,故选D.4.已知f(x)=(x-a)(x-b)+2(a(A)a<α<β(C)α所以α,β为f(x)=(x-a)(x-b)+2与x轴交点的横坐标.
因为a,b为(x-a)(x-b)=0的根,
令g(x)=(x-a)(x-b),
所以a,b为g(x)与x轴交点的横坐标.可知f(x)的图象可由g(x)的图象向上平移2个单位得到,由图知选A.5.不等式x2+ax+4<0的解集不是空集,则实数a的取值范围是 .?解析:因为不等式x2+ax+4<0的解集不是空集,所以Δ=a2-16>0,
所以a<-4或a>4.
所以a的取值范围是(-∞,-4)∪(4,+∞).
答案:(-∞,-4)∪(4,+∞)题型一 三个二次之间的联系课堂探究【例1】 若不等式ax2+bx-1>0的解集是{x|1(1)试求a,b的值;(2)求不等式 >0的解集.方法技巧 一元二次方程ax2+bx+c=0(a≠0)有两个根x1,x2时,二次函数y=ax2+bx+c与x轴有两个交点(x1,0),(x2,0).当已知ax2+bx+c>0(或ax2+bx+ c<0)的解集时,也就知道了ax2+bx+c=0的根,求参数时一般需把根代入方程或利用根与系数的关系(韦达定理)得出.即时训练1-1:已知不等式ax2-3x+6>4的解集为{x|x<1或x>b}.
(1)求a,b;解:(1)原不等式可化为ax2-3x+2>0,
由题意知x=1是方程ax2-3x+2=0的根,
所以a=1.
所以x2-3x+2>0,
所以x<1或x>2,故b=2.(2)解不等式ax2-(ac+b)x+bc<0(c∈R).解: (2)由(1)可知原不等式可化为x2-(c+2)x+2c<0,
即(x-c)(x-2)<0,
①当c>2时,2(1)若对于一切实数x,f(x)<0恒成立,求m的取值范围;(2)对于x∈[1,3],f(x)<-m+5恒成立,求m的取值范围.方法技巧 不等式恒成立求其中参数取值范围的问题通常有以下两种解法:(2)分离参数,构造合适的函数将恒成立问题转化为求函数在给定区间上的最值问题,即
k≥f(x)(k>f(x))恒成立?k≥f(x)max(k>f(x)max);
k≤f(x)(k因为方程2kx2-2x-3k-2=0的两根一个大于1,一个小于1,
①若k>0,则f(1)<0,即2k-2-3k-2<0,所以k>-4.
又k>0,所以k>0.
②若k<0,则f(1)>0,即2k-2-3k-2>0,所以k<-4.
又k<0,所以k<-4.综合①②可知,
k的取值范围为(-∞,-4)∪(0,+∞).题型四 一元二次不等式的实际应用【例4】 某摩托车生产企业,上年度生产车的投入成本为1万元/辆,出厂价为1.2万元/辆,年销售量为1 000辆,本年度为适应市场需要, 计划提高产品档次,适度增加投入成本,若每辆车投入成本增加的比例为x(0(1)写出本年度预计的年利润y与投入成本增加的比例x之间的关系式;解:(1)每辆车投入成本增加的比例为x,
则每辆车投入成本为1×(1+x)万元,出厂价为1.2×(1+0.75x)万元,年销量为1 000×(1+0.6x)辆.
所以y=[1.2×(1+0.75x)-1×(1+x)]×1 000×(1+0.6x),
即y=-60x2+20x+200(0(1)审题:弄清题意,分析条件和结论,理顺数量关系;
(2)建模:建立一元二次不等式模型;
(3)求解:解一元二次不等式;
(4)还原:把数学结论还原为实际问题.即时训练4-1:某单位在对一个长800 m,宽600 m的草坪进行绿化时,是这样想的:中间为矩形绿草坪,四周是等宽的花坛,如图所示,若要保证绿草坪的面积不小于总面积的二分之一,试确定花坛宽度的取值范围.解不等式得x≥600(舍去)或x≤100,
由题意知x>0,
所以0当x在(0,100]内取值时,绿草坪的面积不小于总面积的二分之一.
(B)(-2,2)
(C)(-∞,-2]∪[2,+∞)
(D)(-∞,-2)∪(2,+∞)A解析:由Δ≤0知a2-4≤0,所以-2≤a≤2.3.已知集合P={0,m},Q={x|2x2-5x<0,x∈Z},若P∩Q≠ ,则m等于( )D 解析:因为Q={x|0
因为a,b为(x-a)(x-b)=0的根,
令g(x)=(x-a)(x-b),
所以a,b为g(x)与x轴交点的横坐标.可知f(x)的图象可由g(x)的图象向上平移2个单位得到,由图知选A.5.不等式x2+ax+4<0的解集不是空集,则实数a的取值范围是 .?解析:因为不等式x2+ax+4<0的解集不是空集,所以Δ=a2-16>0,
所以a<-4或a>4.
所以a的取值范围是(-∞,-4)∪(4,+∞).
答案:(-∞,-4)∪(4,+∞)题型一 三个二次之间的联系课堂探究【例1】 若不等式ax2+bx-1>0的解集是{x|1
(1)求a,b;解:(1)原不等式可化为ax2-3x+2>0,
由题意知x=1是方程ax2-3x+2=0的根,
所以a=1.
所以x2-3x+2>0,
所以x<1或x>2,故b=2.(2)解不等式ax2-(ac+b)x+bc<0(c∈R).解: (2)由(1)可知原不等式可化为x2-(c+2)x+2c<0,
即(x-c)(x-2)<0,
①当c>2时,2
k≥f(x)(k>f(x))恒成立?k≥f(x)max(k>f(x)max);
k≤f(x)(k
①若k>0,则f(1)<0,即2k-2-3k-2<0,所以k>-4.
又k>0,所以k>0.
②若k<0,则f(1)>0,即2k-2-3k-2>0,所以k<-4.
又k<0,所以k<-4.综合①②可知,
k的取值范围为(-∞,-4)∪(0,+∞).题型四 一元二次不等式的实际应用【例4】 某摩托车生产企业,上年度生产车的投入成本为1万元/辆,出厂价为1.2万元/辆,年销售量为1 000辆,本年度为适应市场需要, 计划提高产品档次,适度增加投入成本,若每辆车投入成本增加的比例为x(0
则每辆车投入成本为1×(1+x)万元,出厂价为1.2×(1+0.75x)万元,年销量为1 000×(1+0.6x)辆.
所以y=[1.2×(1+0.75x)-1×(1+x)]×1 000×(1+0.6x),
即y=-60x2+20x+200(0
(2)建模:建立一元二次不等式模型;
(3)求解:解一元二次不等式;
(4)还原:把数学结论还原为实际问题.即时训练4-1:某单位在对一个长800 m,宽600 m的草坪进行绿化时,是这样想的:中间为矩形绿草坪,四周是等宽的花坛,如图所示,若要保证绿草坪的面积不小于总面积的二分之一,试确定花坛宽度的取值范围.解不等式得x≥600(舍去)或x≤100,
由题意知x>0,
所以0
