高中数学新人教A版必修5课件:第一章解三角形1.2应用举例第一课时正、余弦定理在实际中的应用(33张)
文档属性
| 名称 | 高中数学新人教A版必修5课件:第一章解三角形1.2应用举例第一课时正、余弦定理在实际中的应用(33张) |

|
|
| 格式 | zip | ||
| 文件大小 | 895.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-20 00:00:00 | ||
图片预览







文档简介
课件33张PPT。1.2 应用举例
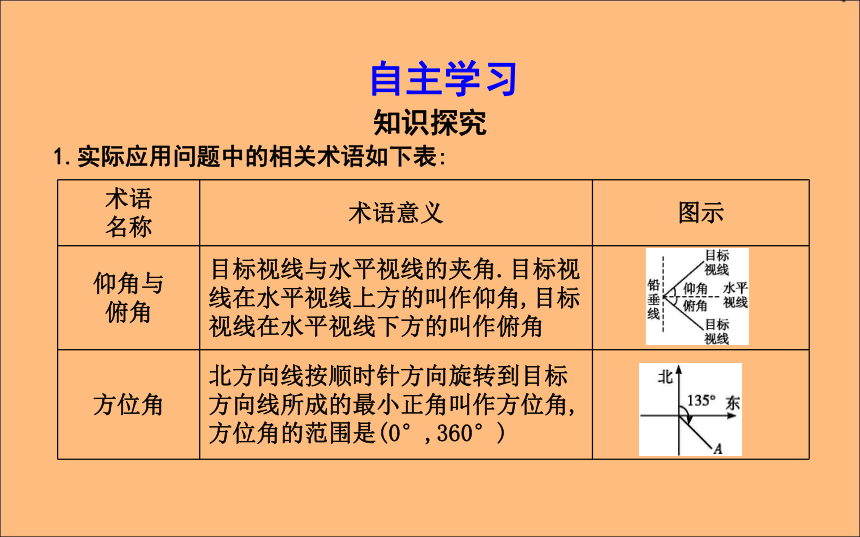
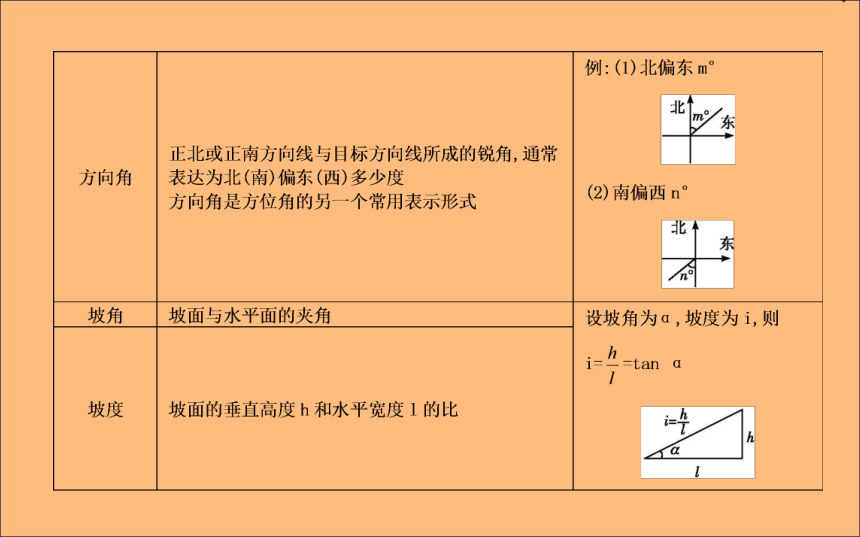
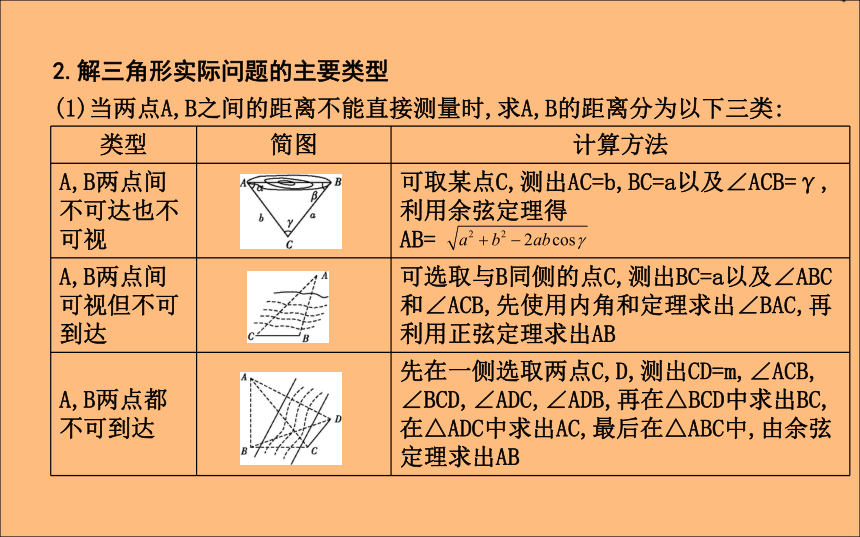
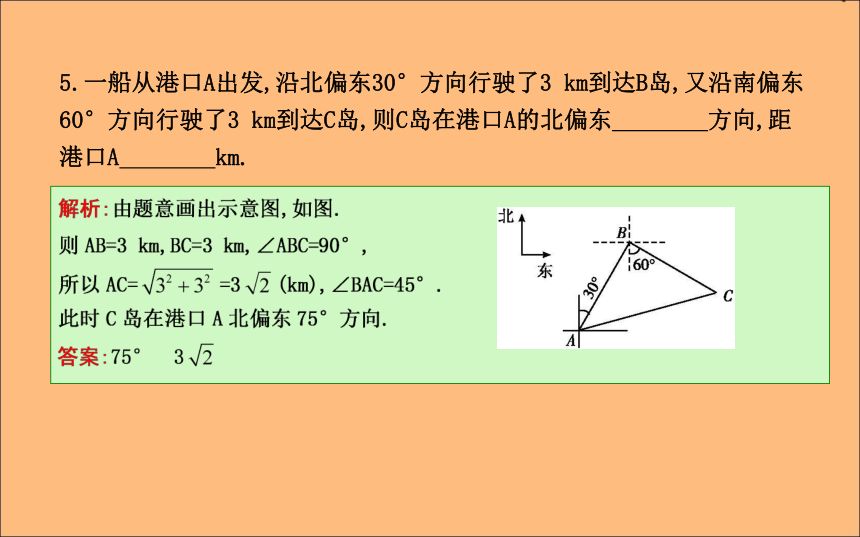
第一课时 正、余弦定理在实际中的应用课标要求:1.能够利用正弦定理、余弦定理解任意三角形.2.能够运用正弦定理、余弦定理解决实际中的测量问题.自主学习知识探究1.实际应用问题中的相关术语如下表:2.解三角形实际问题的主要类型
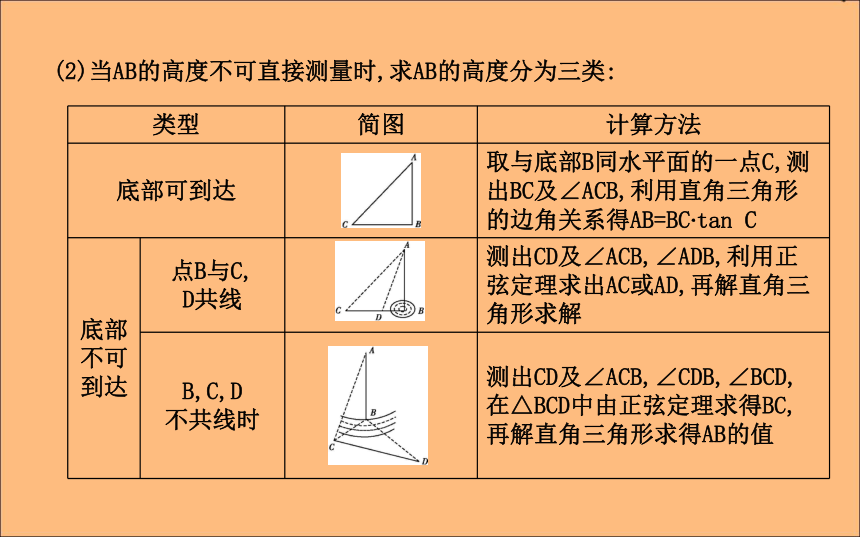
(1)当两点A,B之间的距离不能直接测量时,求A,B的距离分为以下三类:(2)当AB的高度不可直接测量时,求AB的高度分为三类:自我检测1.从A处望B处的仰角为α,从B处望A处的俯角为β,则α,β的关系为( )
(A)α>β (B)α=β
(C)α+β=90° (D)α+β=180°B解析:根据仰角与俯角的定义知α=β.故选B.A2.某次测量中,若A在B的南偏东40°,则B在A的( )
(A)北偏西40° (B)北偏东50°
(C)北偏西50° (D)南偏西50°解析:由方向角的定义知选A.D3.如图,在河岸AC测量河的宽度BC,测量下列四组数据,较适宜的是( )
(A)a,c,α
(B)b,c,α
(C)c,a,β
(D)b,α,β解析:由正弦定理BC= ,故选D.4.如图,甲、乙两楼相距20 m,从乙楼底望甲楼顶的仰角为60°,从甲楼顶望乙楼顶的俯角为30°,则乙楼的高是 m.?5.一船从港口A出发,沿北偏东30°方向行驶了3 km到达B岛,又沿南偏东60°方向行驶了3 km到达C岛,则C岛在港口A的北偏东 方向,距港口A km.?题型一 测量距离问题课堂探究【例1】 (1)甲船在湖中B岛的正南A处,AB=3 km,甲船以8 km/h的速度向正北方向航行,同时乙船自B岛出发,以12 km/h的速度向北偏东60°方向驶去,则行驶15 min时,两船间的距离是( )(2)在某次军事演习中,红方为了准确分析战场形势,在两个相距为 的军事基地C处和D处测得蓝方两支精锐部队分别在A处和B处,且∠ADB=30°,
∠BDC=30°,∠DCA=60°,∠ACB=45°,如图所示,求蓝方这两支精锐部队的距离.误区警示 求距离问题的注意事项
(1)选定或确定所求量所在的三角形.若其他量已知,则直接求解;若有未知量,则把未知量放在另一三角形中求解.
(2)确定用正弦定理还是余弦定理,如果都可用,就选择更便于计算的定理.即时训练1-1:如图所示,隔河看两目标A,B,但不能到达,在岸边选取相距 千米的C,D两点,并测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°
(A,B,C,D在同一平面内),求两目标A,B之间的距离.方法技巧 求两不可到达的点之间的距离问题,通常需要解多个三角形,通过一些相邻三角形公共边、角的相互转化,并综合应用正、余弦定理,来获得待求的距离.题型二 测量高度问题【例2】 (1)如图所示,为测量一树的高度,在地面上选取A,B两点,从A,B两点测得树尖的仰角分别为30°和45°,且A,B两点之间的距离为60 m,则树的高度为( )A(2)如图,为了测量河对岸的塔高AB,有不同的方案,其中之一是选取与塔底B在同一水平面内的两个测点C和D,测得CD=200米,在C点和D点测得塔顶A的仰角分别是45°和30°,且∠CBD=30°,求塔高AB.方法技巧 测量高度问题的方法:由于塔垂直于地面,因此一定会出现直角三角形,应抓住此条件求出直角三角形的某条边,再应用到其他三角形中.问题中,如果既有方向角又有仰(俯)角,在绘制图形时,可画出立体图形和平面图形两个图,以对比分析求解.变式探究:本例中,若将条件改为∠BCD=15°,∠BDC=30°,CD=30,且在C点测得塔顶A的仰角为60°,如何求塔高AB?即时训练2-1:如图,一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北侧一山顶D在西偏北30°的方向上,行驶600 m后到达B处,测得此山顶在西偏北75°的方向上,仰角为30°,则此山的高度CD= m.?题型三 测量角度问题【例3】 (1)如图所示,已知两座灯塔A和B与海洋观察站C的距离相等,灯塔A在观察站C的北偏东40°方向,灯塔B在观察站C的南偏东60°方向,则灯塔A在灯塔B的( )
(A)北偏东10°方向
(B)北偏西10°方向
(C)南偏东10°方向
(D)南偏西10°方向(1)解析:由题意,得∠ACB=180°-(40°+60°)=80°.
因为AC=BC,所以∠A=∠CBA=50°.
因为∠CBD=60°,所以∠ABD=60°-50°=10°.
故灯塔A在灯塔B的北偏西10°方向.故选B.(2)解:若要最快追上走私船,
则两船所用时间相等.
假设在D处相遇,设缉私船用t h在D处追上走私船,如图.方法技巧 测量角度问题也就是通过解三角形求角的问题,求角问题可转化为求该角的三角函数值.若是用余弦定理求得该角的余弦,则该角易确定,若用正弦定理求得该角的正弦,则需讨论解的情况.即时训练3-1:某渔船在航行中不幸遇险,发出呼叫信号,我海军舰艇在A处获悉后,立即测出该渔船在方位角为45°,距离为10 nmile的C处,并测得渔船正沿方位角为105°的方向,以10 nmile/h的速度向某小岛B靠拢,我海军舰艇立即以10 nmile/h的速度前去营救,求舰艇的航向和靠近渔船所需的时间.
第一课时 正、余弦定理在实际中的应用课标要求:1.能够利用正弦定理、余弦定理解任意三角形.2.能够运用正弦定理、余弦定理解决实际中的测量问题.自主学习知识探究1.实际应用问题中的相关术语如下表:2.解三角形实际问题的主要类型
(1)当两点A,B之间的距离不能直接测量时,求A,B的距离分为以下三类:(2)当AB的高度不可直接测量时,求AB的高度分为三类:自我检测1.从A处望B处的仰角为α,从B处望A处的俯角为β,则α,β的关系为( )
(A)α>β (B)α=β
(C)α+β=90° (D)α+β=180°B解析:根据仰角与俯角的定义知α=β.故选B.A2.某次测量中,若A在B的南偏东40°,则B在A的( )
(A)北偏西40° (B)北偏东50°
(C)北偏西50° (D)南偏西50°解析:由方向角的定义知选A.D3.如图,在河岸AC测量河的宽度BC,测量下列四组数据,较适宜的是( )
(A)a,c,α
(B)b,c,α
(C)c,a,β
(D)b,α,β解析:由正弦定理BC= ,故选D.4.如图,甲、乙两楼相距20 m,从乙楼底望甲楼顶的仰角为60°,从甲楼顶望乙楼顶的俯角为30°,则乙楼的高是 m.?5.一船从港口A出发,沿北偏东30°方向行驶了3 km到达B岛,又沿南偏东60°方向行驶了3 km到达C岛,则C岛在港口A的北偏东 方向,距港口A km.?题型一 测量距离问题课堂探究【例1】 (1)甲船在湖中B岛的正南A处,AB=3 km,甲船以8 km/h的速度向正北方向航行,同时乙船自B岛出发,以12 km/h的速度向北偏东60°方向驶去,则行驶15 min时,两船间的距离是( )(2)在某次军事演习中,红方为了准确分析战场形势,在两个相距为 的军事基地C处和D处测得蓝方两支精锐部队分别在A处和B处,且∠ADB=30°,
∠BDC=30°,∠DCA=60°,∠ACB=45°,如图所示,求蓝方这两支精锐部队的距离.误区警示 求距离问题的注意事项
(1)选定或确定所求量所在的三角形.若其他量已知,则直接求解;若有未知量,则把未知量放在另一三角形中求解.
(2)确定用正弦定理还是余弦定理,如果都可用,就选择更便于计算的定理.即时训练1-1:如图所示,隔河看两目标A,B,但不能到达,在岸边选取相距 千米的C,D两点,并测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°
(A,B,C,D在同一平面内),求两目标A,B之间的距离.方法技巧 求两不可到达的点之间的距离问题,通常需要解多个三角形,通过一些相邻三角形公共边、角的相互转化,并综合应用正、余弦定理,来获得待求的距离.题型二 测量高度问题【例2】 (1)如图所示,为测量一树的高度,在地面上选取A,B两点,从A,B两点测得树尖的仰角分别为30°和45°,且A,B两点之间的距离为60 m,则树的高度为( )A(2)如图,为了测量河对岸的塔高AB,有不同的方案,其中之一是选取与塔底B在同一水平面内的两个测点C和D,测得CD=200米,在C点和D点测得塔顶A的仰角分别是45°和30°,且∠CBD=30°,求塔高AB.方法技巧 测量高度问题的方法:由于塔垂直于地面,因此一定会出现直角三角形,应抓住此条件求出直角三角形的某条边,再应用到其他三角形中.问题中,如果既有方向角又有仰(俯)角,在绘制图形时,可画出立体图形和平面图形两个图,以对比分析求解.变式探究:本例中,若将条件改为∠BCD=15°,∠BDC=30°,CD=30,且在C点测得塔顶A的仰角为60°,如何求塔高AB?即时训练2-1:如图,一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北侧一山顶D在西偏北30°的方向上,行驶600 m后到达B处,测得此山顶在西偏北75°的方向上,仰角为30°,则此山的高度CD= m.?题型三 测量角度问题【例3】 (1)如图所示,已知两座灯塔A和B与海洋观察站C的距离相等,灯塔A在观察站C的北偏东40°方向,灯塔B在观察站C的南偏东60°方向,则灯塔A在灯塔B的( )
(A)北偏东10°方向
(B)北偏西10°方向
(C)南偏东10°方向
(D)南偏西10°方向(1)解析:由题意,得∠ACB=180°-(40°+60°)=80°.
因为AC=BC,所以∠A=∠CBA=50°.
因为∠CBD=60°,所以∠ABD=60°-50°=10°.
故灯塔A在灯塔B的北偏西10°方向.故选B.(2)解:若要最快追上走私船,
则两船所用时间相等.
假设在D处相遇,设缉私船用t h在D处追上走私船,如图.方法技巧 测量角度问题也就是通过解三角形求角的问题,求角问题可转化为求该角的三角函数值.若是用余弦定理求得该角的余弦,则该角易确定,若用正弦定理求得该角的正弦,则需讨论解的情况.即时训练3-1:某渔船在航行中不幸遇险,发出呼叫信号,我海军舰艇在A处获悉后,立即测出该渔船在方位角为45°,距离为10 nmile的C处,并测得渔船正沿方位角为105°的方向,以10 nmile/h的速度向某小岛B靠拢,我海军舰艇立即以10 nmile/h的速度前去营救,求舰艇的航向和靠近渔船所需的时间.
