高中数学新人教A版选修2-1课件:第二章圆锥曲线与方程2.2.1椭圆及其标准方程(34张)
文档属性
| 名称 | 高中数学新人教A版选修2-1课件:第二章圆锥曲线与方程2.2.1椭圆及其标准方程(34张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-20 00:00:00 | ||
图片预览











文档简介
课件34张PPT。2.2 椭 圆
2.2.1 椭圆及其标准方程课标要求:1.了解椭圆标准方程的推导.2.理解椭圆的定义及椭圆的标准方程.3.掌握用定义和待定系数法求椭圆的标准方程. 自主学习1.椭圆的定义
(1)椭圆的定义
我们把平面内与两个定点F1,F2的距离的和等于常数(大于|F1F2|)的点的轨迹叫做椭圆(ellipse).
这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距.
(2)椭圆定义的集合
设点M是椭圆上的任意一点,点F1,F2是椭圆的焦点,则由椭圆的定义知,椭圆就是集合P={M||MF1|+|MF2|=常数,常数>|F1F2|>0}.知识探究注意:对定义中限制条件“常数(大于|F1F2|)”的理解
(1)当动点M满足|MF1|+|MF2|=常数>|F1F2|时,动点M的轨迹为椭圆.
(2)当动点M满足|MF1|+|MF2|=常数=|F1F2|时,动点M的轨迹为以F1,F2为两端点的线段.
(3)当动点M满足|MF1|+|MF2|=常数<|F1F2|时,动点M的轨迹不存在.
(4)此定义是推导椭圆方程的依据.
(5)理解椭圆定义要紧扣“到两定点距离之和为定值且大于两定点间的距离”.注意:椭圆标准方程的推导,要充分利用椭圆的对称性,当且仅当椭圆的中心为坐标原点,其焦点在坐标轴上时,椭圆的方程才具有标准形式.
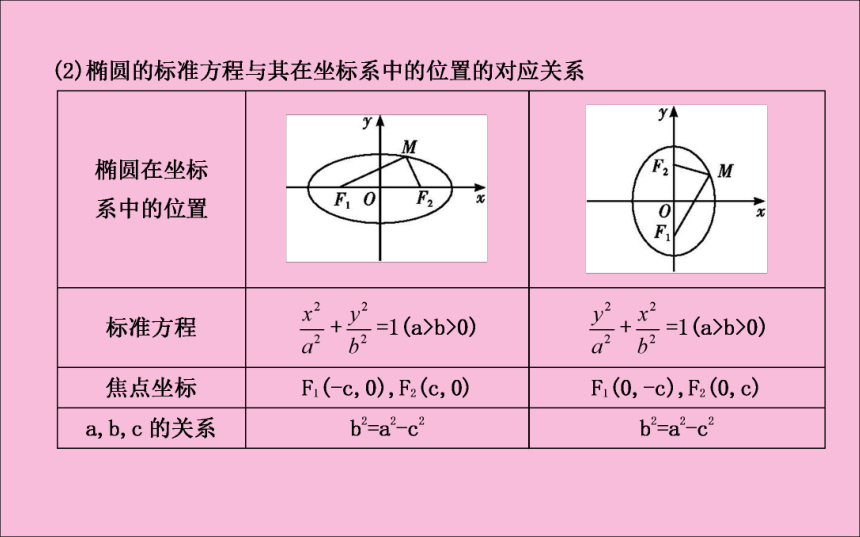
(1)标准方程中根据x2,y2对应的分母的大小可以确定椭圆的焦点在哪条坐标轴上,x2对应的分母大,焦点就在x轴上;y2对应的分母大,焦点就在y轴上.
(2)标准方程中的两个参数a,b确定了椭圆的形状和大小,是椭圆定形的条件,a,b,c三个量满足a2=b2+c2,恰好是一个直角三角形的三条边,构成如图的直角三角形,称为椭圆的“特征三角形”.椭圆的特征三角形清晰地反映了参数a,b,c的几何意义.3.椭圆的焦点三角形
(1)焦点三角形的概念
设M是椭圆上一点,F1,F2为椭圆的焦点,当点M,F1,F2
不在同一条直线上时,它们构成一个三角形——焦
点三角形,如图所示.
(2)焦点三角形的常用公式
①焦点三角形的周长L=2a+2c.
②在△MF1F2中,由余弦定理可得|F1F2|2=|MF1|2+|MF2|2-2|MF1||MF2|cos∠F1MF2.自我检测D 解析:|PF1|+|PF2|=2a=10.DC解析:由已知,k-4>10-k>0,解得7(2)与焦点三角形有关的问题,常考虑定义、余弦定理相结合求解,注意方程思想的应用.答案:(1)C题型二椭圆标准方程的理解 求参数的范围就是根据条件列出以参数为未知量的不等式(组)或方程(组),把问题转化为不等式(组)或方程(组)的求解问题.
本题如果未知焦点所在的位置,就要分两种情形分别列式求解.方法技巧(2)(2016·山东济南检测)如果椭圆5x2+ky2=5的一个焦点是(0,2),那么k= .?答案:(2)1求椭圆的标准方程题型三【例3】 求满足下列条件的椭圆的标准方程.
(1)a=5,c=2,焦点在y轴上;(2)焦距为8,椭圆上一点到两焦点的距离之和为12; 求椭圆方程的方法
(1)求椭圆的方程,可以利用定义求出参数a,b,c其中的两个量;也可以用待定系数法构造三者之间的关系.但是要注意先确定焦点所在的位置,其主要步骤可归纳为“先定位,后定量”.
(2)当焦点位置不确定时,可设椭圆方程为mx2+ny2=1(m>0,n>0,m≠n).因为它包括焦点在x轴上(mn)两类情况,所以可以避免分类讨论,从而达到了简化运算的目的.易错警示即时训练3-1:求适合下列条件的椭圆的标准方程:
(1)两个焦点的坐标分别是(-2,0),(2,0),椭圆上一点P到两焦点距离之和等于6;(2)椭圆的焦点为F1(0,-5),F2(0,5),点P(3,4)是椭圆上的一个点.
2.2.1 椭圆及其标准方程课标要求:1.了解椭圆标准方程的推导.2.理解椭圆的定义及椭圆的标准方程.3.掌握用定义和待定系数法求椭圆的标准方程. 自主学习1.椭圆的定义
(1)椭圆的定义
我们把平面内与两个定点F1,F2的距离的和等于常数(大于|F1F2|)的点的轨迹叫做椭圆(ellipse).
这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距.
(2)椭圆定义的集合
设点M是椭圆上的任意一点,点F1,F2是椭圆的焦点,则由椭圆的定义知,椭圆就是集合P={M||MF1|+|MF2|=常数,常数>|F1F2|>0}.知识探究注意:对定义中限制条件“常数(大于|F1F2|)”的理解
(1)当动点M满足|MF1|+|MF2|=常数>|F1F2|时,动点M的轨迹为椭圆.
(2)当动点M满足|MF1|+|MF2|=常数=|F1F2|时,动点M的轨迹为以F1,F2为两端点的线段.
(3)当动点M满足|MF1|+|MF2|=常数<|F1F2|时,动点M的轨迹不存在.
(4)此定义是推导椭圆方程的依据.
(5)理解椭圆定义要紧扣“到两定点距离之和为定值且大于两定点间的距离”.注意:椭圆标准方程的推导,要充分利用椭圆的对称性,当且仅当椭圆的中心为坐标原点,其焦点在坐标轴上时,椭圆的方程才具有标准形式.
(1)标准方程中根据x2,y2对应的分母的大小可以确定椭圆的焦点在哪条坐标轴上,x2对应的分母大,焦点就在x轴上;y2对应的分母大,焦点就在y轴上.
(2)标准方程中的两个参数a,b确定了椭圆的形状和大小,是椭圆定形的条件,a,b,c三个量满足a2=b2+c2,恰好是一个直角三角形的三条边,构成如图的直角三角形,称为椭圆的“特征三角形”.椭圆的特征三角形清晰地反映了参数a,b,c的几何意义.3.椭圆的焦点三角形
(1)焦点三角形的概念
设M是椭圆上一点,F1,F2为椭圆的焦点,当点M,F1,F2
不在同一条直线上时,它们构成一个三角形——焦
点三角形,如图所示.
(2)焦点三角形的常用公式
①焦点三角形的周长L=2a+2c.
②在△MF1F2中,由余弦定理可得|F1F2|2=|MF1|2+|MF2|2-2|MF1||MF2|cos∠F1MF2.自我检测D 解析:|PF1|+|PF2|=2a=10.DC解析:由已知,k-4>10-k>0,解得7
本题如果未知焦点所在的位置,就要分两种情形分别列式求解.方法技巧(2)(2016·山东济南检测)如果椭圆5x2+ky2=5的一个焦点是(0,2),那么k= .?答案:(2)1求椭圆的标准方程题型三【例3】 求满足下列条件的椭圆的标准方程.
(1)a=5,c=2,焦点在y轴上;(2)焦距为8,椭圆上一点到两焦点的距离之和为12; 求椭圆方程的方法
(1)求椭圆的方程,可以利用定义求出参数a,b,c其中的两个量;也可以用待定系数法构造三者之间的关系.但是要注意先确定焦点所在的位置,其主要步骤可归纳为“先定位,后定量”.
(2)当焦点位置不确定时,可设椭圆方程为mx2+ny2=1(m>0,n>0,m≠n).因为它包括焦点在x轴上(m
(1)两个焦点的坐标分别是(-2,0),(2,0),椭圆上一点P到两焦点距离之和等于6;(2)椭圆的焦点为F1(0,-5),F2(0,5),点P(3,4)是椭圆上的一个点.
