高中数学新人教A版选修2-1课件:第二章圆锥曲线与方程2.3.1双曲线及其标准方程(34张)
文档属性
| 名称 | 高中数学新人教A版选修2-1课件:第二章圆锥曲线与方程2.3.1双曲线及其标准方程(34张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-20 00:00:00 | ||
图片预览










文档简介
课件34张PPT。2.3 双曲线
2.3.1 双曲线及其标准方程课标要求:1.了解双曲线的定义、几何图形和标准方程的推导过程.2.掌握双曲线的标准方程.3.会利用双曲线的定义和标准方程解决简单的问题. 自主学习知识探究1.双曲线的定义
平面内与两个定点F1,F2的距离的差的绝对值等于非零常数(小于|F1F2|)的点的轨迹叫做双曲线.
这两个定点叫做双曲线的焦点,两焦点间的距离叫做双曲线的焦距.
2.双曲线定义的集合表示
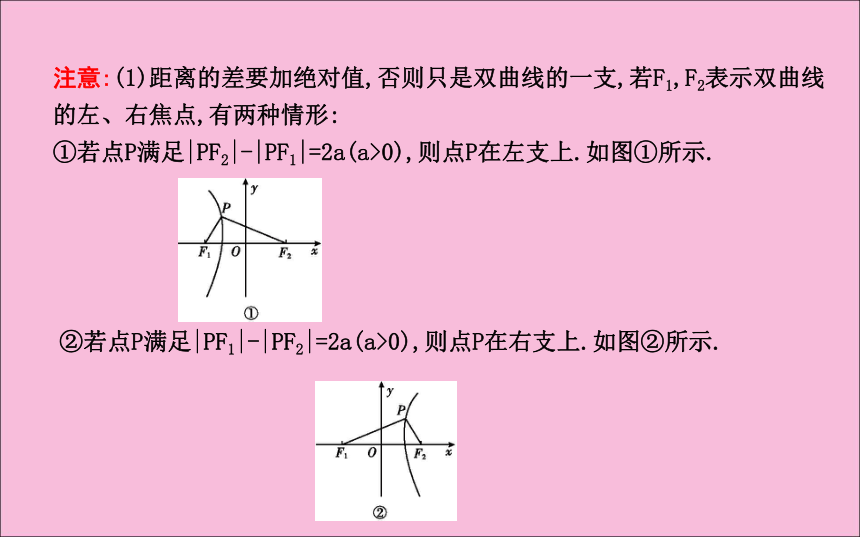
设点M是双曲线上任意一点,点F1,F2是双曲线的焦点,则由双曲线的定义可知,双曲线可以视为动点M的集合,即点集P={M|||MF1|-|MF2||=常数,常数大于0且小于|F1F2|}.注意:(1)距离的差要加绝对值,否则只是双曲线的一支,若F1,F2表示双曲线的左、右焦点,有两种情形:
①若点P满足|PF2|-|PF1|=2a(a>0),则点P在左支上.如图①所示.②若点P满足|PF1|-|PF2|=2a(a>0),则点P在右支上.如图②所示.(2)注意定义中的“小于|F1F2|”这一限制条件,其根据是“三角形两边之差小于第三边”.
①若2a=2c,即||PF1|-|PF2||=|F1F2|,根据平面几何知识,当|PF1|-|PF2|= |F1F2|时,动点轨迹是以F2为端点向右延伸的一条射线;当|PF2|-|PF1|=|F1F2|时,动点轨迹是以F1为端点向左延伸的一条射线.
②若2a>2c,即||PF1|-|PF2||>|F1F2|,根据平面几何知识,动点轨迹不存在.3.双曲线的标准方程注意:(1)标准方程中的两个参数a和b,确定了双曲线的形状和大小,是双曲线的定形条件,这里b2=c2-a2,它们恰好为一个直角三角形的三条边,其中c为斜边.注意与椭圆中b2=a2-c2相区别,在椭圆中a>b>0,而双曲线中,a,b大小则不确定.
(2)焦点F1,F2的位置,是双曲线定位的条件,它决定了双曲线标准方程的类型.可以根据项的正负来判断焦点所在的位置,即x2项的系数是正的,那么焦点在x轴上;y2项的系数是正的,那么焦点在y轴上.简言之,“焦点跟着正项走”.自我检测D解析:双曲线的焦点坐标为(±5,0),令|PF2|=15,由||PF1|-|PF2||=8,解得|PF1|=23或|PF1|=7.D3.若k>1,则关于x,y的方程(1-k)x2+y2=k2-1所表示的曲线是( )
(A)焦点在x轴上的椭圆
(B)焦点在y轴上的椭圆
(C)焦点在y轴上的双曲线
(D)焦点在x轴上的双曲线C解析:由已知a2=m,b2=3, 所以m+3=9,所以m=6.
答案:65.一动圆过定点A(-4,0),且与定圆B:(x-4)2+y2=16相外切,则动圆圆心的轨迹方程为 .?题型一 双曲线定义的理解及应用 课堂探究【例1】 (1)已知F1(-8,3),F2(2,3),动点P满足|PF1|-|PF2|=10,则P点的轨迹是( )
(A)双曲线 (B)双曲线的一支
(C)直线 (D)一条射线解析:(1)F1,F2是定点,且|F1F2|=10,所以满足条件|PF1|-|PF2|=10的点P的轨迹应为一条射线.故选D.
答案:(1)D答案:(2)16答案:32误区警示 (1)在解决与双曲线有关的焦点三角形问题时,应注意双曲线定义条件||PF1|-|PF2||=2a的应用.
(2)解题的关键是“|PF1|·|PF2|”形式的“配凑”,将双曲线定义及图形的平面几何性质(结合正、余弦定理)“和谐”地结合起来,注意整体思想的应用,从而达到简化运算的目的.(2)已知一个动点P(x,y)到两个定点F1(-1,0),F2(1,0)的距离差的绝对值为定值a(a≥0),求点P的轨迹.解:(2)因为|F1F2|=2,
①当a=2时,轨迹是两条射线y=0(x≥1)或y=0(x≤-1);
②当a=0时,轨迹是线段F1F2的垂直平分线,即y轴,方程x=0;
③当0④当a>2时,轨迹不存在.题型二双曲线标准方程的求法方法技巧 利用待定系数法求双曲线标准方程的步骤:双曲线标准方程的理解题型三【例3】 (1)若θ是第三象限角,则方程x2+y2sin θ=cos θ表示的曲线是( )
(A)焦点在y轴上的双曲线
(B)焦点在x轴上的双曲线
(C)焦点在y轴上的椭圆
(D)焦点在x轴上的椭圆解析:(1)由题意知(k+1)(1-k)<0,
即(k+1)(k-1)>0,解得k>1或k<-1.
故选D.(2)已知m,n为两个不相等的非零实数,则方程mx-y+n=0与nx2+my2=mn所表示的曲线可能是( )解析:(2)A中,由直线位置可知,m>0,n<0,曲线应为双曲线,故A错;B中,由直线位置可知,m<0,n>0,曲线应为双曲线,故B错;C中,由直线位置可知,m>0,n<0,曲线为焦点在x轴上的双曲线,故C正确;D中,由直线位置可知,m>0,n>0,曲线应为椭圆,故D错.故选C.
2.3.1 双曲线及其标准方程课标要求:1.了解双曲线的定义、几何图形和标准方程的推导过程.2.掌握双曲线的标准方程.3.会利用双曲线的定义和标准方程解决简单的问题. 自主学习知识探究1.双曲线的定义
平面内与两个定点F1,F2的距离的差的绝对值等于非零常数(小于|F1F2|)的点的轨迹叫做双曲线.
这两个定点叫做双曲线的焦点,两焦点间的距离叫做双曲线的焦距.
2.双曲线定义的集合表示
设点M是双曲线上任意一点,点F1,F2是双曲线的焦点,则由双曲线的定义可知,双曲线可以视为动点M的集合,即点集P={M|||MF1|-|MF2||=常数,常数大于0且小于|F1F2|}.注意:(1)距离的差要加绝对值,否则只是双曲线的一支,若F1,F2表示双曲线的左、右焦点,有两种情形:
①若点P满足|PF2|-|PF1|=2a(a>0),则点P在左支上.如图①所示.②若点P满足|PF1|-|PF2|=2a(a>0),则点P在右支上.如图②所示.(2)注意定义中的“小于|F1F2|”这一限制条件,其根据是“三角形两边之差小于第三边”.
①若2a=2c,即||PF1|-|PF2||=|F1F2|,根据平面几何知识,当|PF1|-|PF2|= |F1F2|时,动点轨迹是以F2为端点向右延伸的一条射线;当|PF2|-|PF1|=|F1F2|时,动点轨迹是以F1为端点向左延伸的一条射线.
②若2a>2c,即||PF1|-|PF2||>|F1F2|,根据平面几何知识,动点轨迹不存在.3.双曲线的标准方程注意:(1)标准方程中的两个参数a和b,确定了双曲线的形状和大小,是双曲线的定形条件,这里b2=c2-a2,它们恰好为一个直角三角形的三条边,其中c为斜边.注意与椭圆中b2=a2-c2相区别,在椭圆中a>b>0,而双曲线中,a,b大小则不确定.
(2)焦点F1,F2的位置,是双曲线定位的条件,它决定了双曲线标准方程的类型.可以根据项的正负来判断焦点所在的位置,即x2项的系数是正的,那么焦点在x轴上;y2项的系数是正的,那么焦点在y轴上.简言之,“焦点跟着正项走”.自我检测D解析:双曲线的焦点坐标为(±5,0),令|PF2|=15,由||PF1|-|PF2||=8,解得|PF1|=23或|PF1|=7.D3.若k>1,则关于x,y的方程(1-k)x2+y2=k2-1所表示的曲线是( )
(A)焦点在x轴上的椭圆
(B)焦点在y轴上的椭圆
(C)焦点在y轴上的双曲线
(D)焦点在x轴上的双曲线C解析:由已知a2=m,b2=3, 所以m+3=9,所以m=6.
答案:65.一动圆过定点A(-4,0),且与定圆B:(x-4)2+y2=16相外切,则动圆圆心的轨迹方程为 .?题型一 双曲线定义的理解及应用 课堂探究【例1】 (1)已知F1(-8,3),F2(2,3),动点P满足|PF1|-|PF2|=10,则P点的轨迹是( )
(A)双曲线 (B)双曲线的一支
(C)直线 (D)一条射线解析:(1)F1,F2是定点,且|F1F2|=10,所以满足条件|PF1|-|PF2|=10的点P的轨迹应为一条射线.故选D.
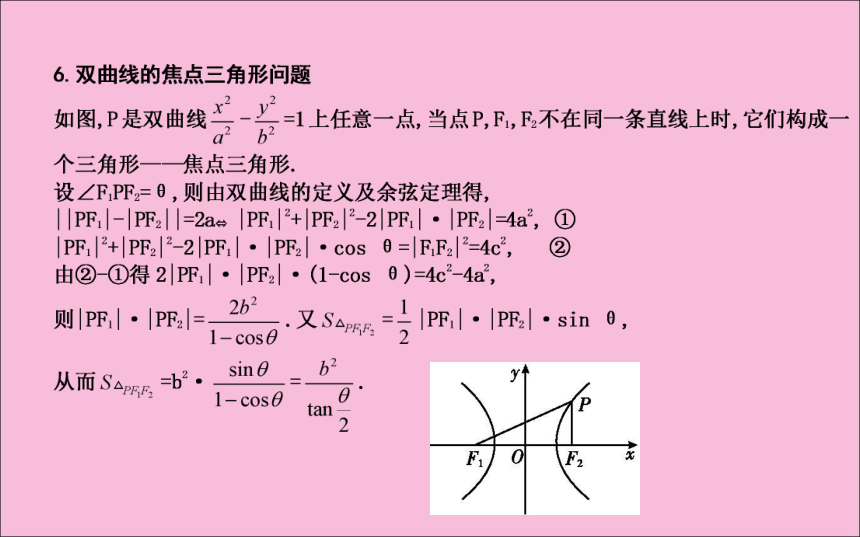
答案:(1)D答案:(2)16答案:32误区警示 (1)在解决与双曲线有关的焦点三角形问题时,应注意双曲线定义条件||PF1|-|PF2||=2a的应用.
(2)解题的关键是“|PF1|·|PF2|”形式的“配凑”,将双曲线定义及图形的平面几何性质(结合正、余弦定理)“和谐”地结合起来,注意整体思想的应用,从而达到简化运算的目的.(2)已知一个动点P(x,y)到两个定点F1(-1,0),F2(1,0)的距离差的绝对值为定值a(a≥0),求点P的轨迹.解:(2)因为|F1F2|=2,
①当a=2时,轨迹是两条射线y=0(x≥1)或y=0(x≤-1);
②当a=0时,轨迹是线段F1F2的垂直平分线,即y轴,方程x=0;
③当0
(A)焦点在y轴上的双曲线
(B)焦点在x轴上的双曲线
(C)焦点在y轴上的椭圆
(D)焦点在x轴上的椭圆解析:(1)由题意知(k+1)(1-k)<0,
即(k+1)(k-1)>0,解得k>1或k<-1.
故选D.(2)已知m,n为两个不相等的非零实数,则方程mx-y+n=0与nx2+my2=mn所表示的曲线可能是( )解析:(2)A中,由直线位置可知,m>0,n<0,曲线应为双曲线,故A错;B中,由直线位置可知,m<0,n>0,曲线应为双曲线,故B错;C中,由直线位置可知,m>0,n<0,曲线为焦点在x轴上的双曲线,故C正确;D中,由直线位置可知,m>0,n>0,曲线应为椭圆,故D错.故选C.
