高中数学新人教A版选修2-1课件:第二章圆锥曲线与方程2.3.2双曲线的简单几何性质(39张)
文档属性
| 名称 | 高中数学新人教A版选修2-1课件:第二章圆锥曲线与方程2.3.2双曲线的简单几何性质(39张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-20 19:40:08 | ||
图片预览











文档简介
课件39张PPT。2.3.2 双曲线的简单几何性质课标要求:1.掌握双曲线的简单几何性质.2.能够利用双曲线的简单几何性质解题.3.能区分椭圆与双曲线的性质. 自主学习知识探究2.对称性
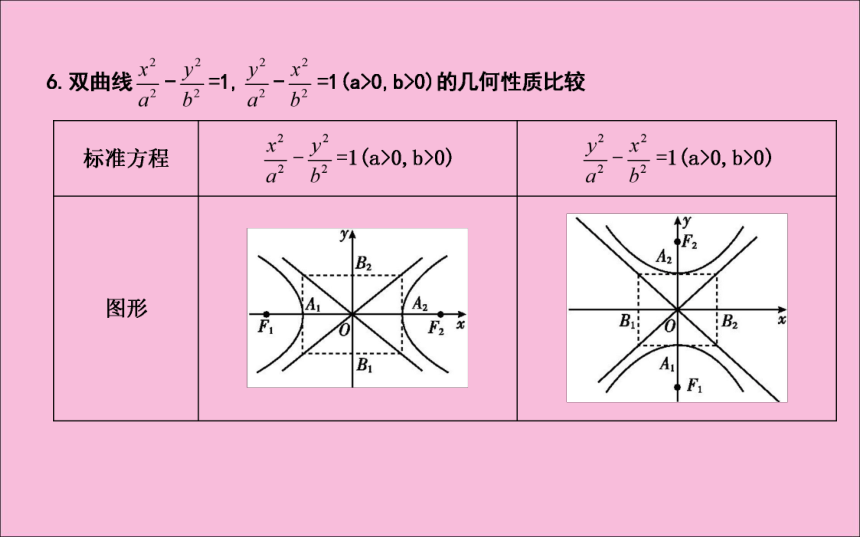
以-x代x可得双曲线关于y轴对称;以-y代y可得双曲线关于x轴对称;以-x代x,-y代y可得双曲线关于原点对称.即坐标轴是双曲线的对称轴,原点是双曲线的对称中心.双曲线的对称中心叫做双曲线的中心.(2)实轴、虚轴
线段A1A2叫做双曲线的实轴,它的长等于2a,a叫做双曲线的实半轴长;
线段B1B2叫做双曲线的虚轴,它的长等于2b,b叫做双曲线的虚半轴长.(2)范围
由c>a>0可知双曲线的离心率e>1.7.等轴双曲线与共轭双曲线
(1)实轴和虚轴等长的双曲线叫做等轴双曲线,等轴双曲线有如下性质:
①方程形式为x2-y2=λ(λ≠0);
②渐近线方程为y=±x,它们互相垂直,并且平分双曲线实轴和虚轴所成的角;②两个共轭双曲线有相同的焦距;自我检测DBC题型一 双曲线的简单几何性质 课堂探究【例1】 (10分)求双曲线nx2-my2=mn(m>0,n>0)的实半轴长、虚半轴长、焦点坐标、离心率、顶点坐标和渐近线方程.变式探究:将本例双曲线方程改为“4x2-y2=-4”,试求解之.方法技巧 由双曲线的标准方程求几何性质的四个步骤(2)求双曲线9x2-y2=81的实轴长、虚轴长、顶点坐标、焦点坐标、渐近线方程、离心率.题型二由几何性质求双曲线的方程答案:(1)C 答案:(2)A 方法技巧⑤渐近线为y=kx的双曲线方程可设为k2x2-y2=λ(λ≠0).
⑥渐近线为ax±by=0的双曲线方程可设为a2x2-b2y2=λ(λ≠0).(3)与双曲线x2-2y2=2有公共的渐近线,且过点M(2,-2).(5)过点P(2,-1),渐近线方程是y=±3x.直线与双曲线的位置关系题型三【例3】 已知双曲线x2-y2=4,直线l:y=k(x-1),试在下列条件下讨论实数k的取值范围.
(1)直线l与双曲线有两个公共点;(2)直线l与双曲线有且只有一个公共点;
(3)直线l与双曲线没有公共点.题后反思 直线与双曲线位置关系的处理方法
把直线与双曲线的方程联立成方程组,通过消元化为一元二次方程形式,在二次项系数不为零的情况下考查方程的判别式:
(1)Δ>0时,直线与双曲线有两个不同的交点.
(2)Δ=0时,直线与双曲线只有一个公共点.
(3)Δ<0时,直线与双曲线没有公共点.
当二次项系数为0时,此时直线与双曲线的渐近线平行,直线与双曲线只有一个公共点.即时训练3-1:直线l:y=kx+1与双曲线C:2x2-y2=1的右支交于不同的两点A,B.
(1)求实数k的取值范围;(2)是否存在实数k,使得以线段AB为直径的圆经过双曲线C的右焦点F?若存在,求出k的值;若不存在,说明理由.
以-x代x可得双曲线关于y轴对称;以-y代y可得双曲线关于x轴对称;以-x代x,-y代y可得双曲线关于原点对称.即坐标轴是双曲线的对称轴,原点是双曲线的对称中心.双曲线的对称中心叫做双曲线的中心.(2)实轴、虚轴
线段A1A2叫做双曲线的实轴,它的长等于2a,a叫做双曲线的实半轴长;
线段B1B2叫做双曲线的虚轴,它的长等于2b,b叫做双曲线的虚半轴长.(2)范围
由c>a>0可知双曲线的离心率e>1.7.等轴双曲线与共轭双曲线
(1)实轴和虚轴等长的双曲线叫做等轴双曲线,等轴双曲线有如下性质:
①方程形式为x2-y2=λ(λ≠0);
②渐近线方程为y=±x,它们互相垂直,并且平分双曲线实轴和虚轴所成的角;②两个共轭双曲线有相同的焦距;自我检测DBC题型一 双曲线的简单几何性质 课堂探究【例1】 (10分)求双曲线nx2-my2=mn(m>0,n>0)的实半轴长、虚半轴长、焦点坐标、离心率、顶点坐标和渐近线方程.变式探究:将本例双曲线方程改为“4x2-y2=-4”,试求解之.方法技巧 由双曲线的标准方程求几何性质的四个步骤(2)求双曲线9x2-y2=81的实轴长、虚轴长、顶点坐标、焦点坐标、渐近线方程、离心率.题型二由几何性质求双曲线的方程答案:(1)C 答案:(2)A 方法技巧⑤渐近线为y=kx的双曲线方程可设为k2x2-y2=λ(λ≠0).
⑥渐近线为ax±by=0的双曲线方程可设为a2x2-b2y2=λ(λ≠0).(3)与双曲线x2-2y2=2有公共的渐近线,且过点M(2,-2).(5)过点P(2,-1),渐近线方程是y=±3x.直线与双曲线的位置关系题型三【例3】 已知双曲线x2-y2=4,直线l:y=k(x-1),试在下列条件下讨论实数k的取值范围.
(1)直线l与双曲线有两个公共点;(2)直线l与双曲线有且只有一个公共点;
(3)直线l与双曲线没有公共点.题后反思 直线与双曲线位置关系的处理方法
把直线与双曲线的方程联立成方程组,通过消元化为一元二次方程形式,在二次项系数不为零的情况下考查方程的判别式:
(1)Δ>0时,直线与双曲线有两个不同的交点.
(2)Δ=0时,直线与双曲线只有一个公共点.
(3)Δ<0时,直线与双曲线没有公共点.
当二次项系数为0时,此时直线与双曲线的渐近线平行,直线与双曲线只有一个公共点.即时训练3-1:直线l:y=kx+1与双曲线C:2x2-y2=1的右支交于不同的两点A,B.
(1)求实数k的取值范围;(2)是否存在实数k,使得以线段AB为直径的圆经过双曲线C的右焦点F?若存在,求出k的值;若不存在,说明理由.
