高中数学新人教A版选修2-1课件:第二章圆锥曲线与方程2.4.2抛物线的简单几何性质(33张)
文档属性
| 名称 | 高中数学新人教A版选修2-1课件:第二章圆锥曲线与方程2.4.2抛物线的简单几何性质(33张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-20 00:00:00 | ||
图片预览











文档简介
课件33张PPT。2.4.2 抛物线的简单几何性质课标要求:1.掌握抛物线的简单几何性质,并能应用性质解题.2.理解直线与抛物线的位置关系. 自主学习知识探究1.抛物线y2=2px(p>0)的简单几何性质
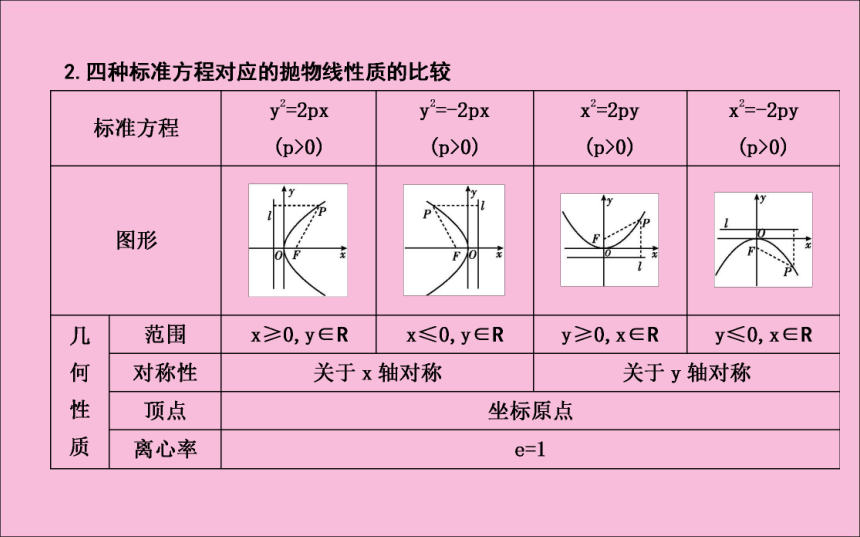
(1)范围
由p>0和方程y2=2px可知,对于抛物线y2=2px(p>0)上的点M(x,y),x≥0,所以这条抛物线在y轴的右侧,开口方向与x轴正向相同;当x的值增大时,|y|也增大,这说明抛物线向右上方和右下方无限延伸.
(2)对称性
以-y代替y,方程y2=2px(p>0)不变,所以这条抛物线关于x轴对称.我们把抛物线的对称轴叫做抛物线的轴.(3)顶点
抛物线和它的轴的交点叫做抛物线的顶点.在方程y2=2px(p>0)中,当y=0时,x=0,因此抛物线y2=2px(p>0)的顶点就是坐标原点.
(4)离心率
抛物线上的点M到焦点的距离和它到准线的距离之比,叫做抛物线的离心率,用e表示.由抛物线的定义可知,e=1.3.直线与抛物线的位置关系
直线与抛物线有三种位置关系:相离、相切、相交.
(1)直线的斜率存在时,设直线y=kx+m与抛物线y2=2px(p>0)相交于A(x1,y1),B(x2,y2)两点,将y=kx+m代入y2=2px,消去y并化简,得k2x2+2(mk-p)x+m2=0.
①当k=0时,直线平行于抛物线的对称轴或与对称轴重合,直线与抛物线只有一个公 共点.
②当k≠0时,判别式Δ>0?直线与抛物线相交,有两个公共点;判别式Δ=0?直线与抛物线相切,有且只有一个公共点;判别式Δ<0?直线与抛物线相离,没有公共点.
(2)直线的斜率不存在时,设直线l:x=m,抛物线:y2=2px(p>0).显然,当m<0时,直线与抛物线相离,无交点;当m=0时,直线与抛物线相切,有一个交点;当m>0时,直线与抛物线相交,有两个交点.(2)通径在反映抛物线开口大小上的作用
线段AB叫做抛物线的通径,长度为2p,这是常数2p的又一几何意义,所以p越大,通径越大,即抛物线的开口越大;反之,p越小,通径越小,即抛物线的开口越小.通径是所有焦点弦中最短的弦.自我检测1.设抛物线的顶点在原点,准线方程为x=-2,则抛物线的方程是( )
(A)y2=-8x (B)y2=8x
(C)y2=-4x (D)y2=4xBB3.已知直线y=kx-k及抛物线y2=2px(p>0),则( )
(A)直线与抛物线有一个公共点 (B)直线与抛物线有两个公共点
(C)直线与抛物线有一个或两个公共点 (D)直线与抛物线可能没有公共点C4.过抛物线y2=4x的焦点作直线交抛物线于A(x1,y1),B(x2,y2)两点,若x1+x2 =6,则|AB|= .?答案:85.过抛物线y2=4x的顶点O作互相垂直的两弦OM,ON,则M的横坐标x1与N的横坐标x2之积为 .?答案:16题型一抛物线简单几何性质的应用 课堂探究【例1】 已知抛物线y2=8x,
(1)求出该抛物线的顶点、焦点、准线、对称轴、变量x的范围;解:(1)抛物线y2=8x的顶点、焦点、准线、对称轴、变量x的范围分别为(0,0),(2,0),x=-2,x轴,x≥0.(2)以坐标原点O为顶点,作抛物线的内接等腰三角形OAB,|OA|=|OB|,若焦点F是△OAB的重心,求△OAB的周长.易错警示 抛物线的几何性质(对称性、范围等)在解决抛物线问题时,有着广泛的应用,但在解题过程中又容易忽视这些隐含条件,如抛物线的对称性、准线与对称轴垂直等,解题时应注意挖掘并充分利用这些隐含条件.(2)已知抛物线C的顶点在原点,焦点F在x轴正半轴上,设A,B是抛物线C上的两个动点(AB不垂直于x轴),且|AF|+|BF|=8,线段AB的垂直平分线恒经过定点Q(6,0),求此抛物线方程.题型二直线与抛物线的位置关系【例2】 已知直线l:y=k(x+1)与抛物线C:y2=4x.问:k为何值时,直线l与抛物线C有两个交点,一个交点,无交点?②若直线与抛物线有一个交点,
则k2=0或k2≠0时,Δ=0.
解得k=0或k=±1.
所以当k=0或k=±1时,直线l和抛物线C有一个交点.
③若直线与抛物线无交点,
则k2≠0且Δ<0.
解得k>1或k<-1.
所以当k>1或k<-1时,直线l和抛物线C无交点.题后反思 研究直线和抛物线的位置关系时,由于消元后所得的方程中含参数,因此要注意分二次项系数为0和不为0两种情况讨论.(2)过点(-3,2)的直线与抛物线y2=4x只有一个公共点,求此直线方程.抛物线的焦点弦问题题型三【例3】 已知直线l经过抛物线y2=6x的焦点F,且与抛物线相交于A,B两点.若直线l的倾斜角为60°,求|AB|的值.变式探究:若本例中“直线l的倾斜角为60°”改为“|AB|=9”,求线段AB的中点M到准线的距离.方法技巧 求圆锥曲线的弦长时,为简化计算常常借助根与系数的关系,这样可以避免分别求x1,x2(或y1,y2)的麻烦,如果是利用弦长求参数的问题,只需要列出参数的方程或不等式即可求解,而x1,x2(或y1,y2)一般是求不出来的.(3)以AB为直径的圆与抛物线的准线相切.题型四抛物线中的最值问题(2)在抛物线上求一点P,使P到直线x-y+3=0的距离最短,并求出距离的最小值.题后反思(2)点P在抛物线2y2=x上,点Q在圆(x-2)2+y2=1上,求|PQ|的最小值.
(1)范围
由p>0和方程y2=2px可知,对于抛物线y2=2px(p>0)上的点M(x,y),x≥0,所以这条抛物线在y轴的右侧,开口方向与x轴正向相同;当x的值增大时,|y|也增大,这说明抛物线向右上方和右下方无限延伸.
(2)对称性
以-y代替y,方程y2=2px(p>0)不变,所以这条抛物线关于x轴对称.我们把抛物线的对称轴叫做抛物线的轴.(3)顶点
抛物线和它的轴的交点叫做抛物线的顶点.在方程y2=2px(p>0)中,当y=0时,x=0,因此抛物线y2=2px(p>0)的顶点就是坐标原点.
(4)离心率
抛物线上的点M到焦点的距离和它到准线的距离之比,叫做抛物线的离心率,用e表示.由抛物线的定义可知,e=1.3.直线与抛物线的位置关系
直线与抛物线有三种位置关系:相离、相切、相交.
(1)直线的斜率存在时,设直线y=kx+m与抛物线y2=2px(p>0)相交于A(x1,y1),B(x2,y2)两点,将y=kx+m代入y2=2px,消去y并化简,得k2x2+2(mk-p)x+m2=0.
①当k=0时,直线平行于抛物线的对称轴或与对称轴重合,直线与抛物线只有一个公 共点.
②当k≠0时,判别式Δ>0?直线与抛物线相交,有两个公共点;判别式Δ=0?直线与抛物线相切,有且只有一个公共点;判别式Δ<0?直线与抛物线相离,没有公共点.
(2)直线的斜率不存在时,设直线l:x=m,抛物线:y2=2px(p>0).显然,当m<0时,直线与抛物线相离,无交点;当m=0时,直线与抛物线相切,有一个交点;当m>0时,直线与抛物线相交,有两个交点.(2)通径在反映抛物线开口大小上的作用
线段AB叫做抛物线的通径,长度为2p,这是常数2p的又一几何意义,所以p越大,通径越大,即抛物线的开口越大;反之,p越小,通径越小,即抛物线的开口越小.通径是所有焦点弦中最短的弦.自我检测1.设抛物线的顶点在原点,准线方程为x=-2,则抛物线的方程是( )
(A)y2=-8x (B)y2=8x
(C)y2=-4x (D)y2=4xBB3.已知直线y=kx-k及抛物线y2=2px(p>0),则( )
(A)直线与抛物线有一个公共点 (B)直线与抛物线有两个公共点
(C)直线与抛物线有一个或两个公共点 (D)直线与抛物线可能没有公共点C4.过抛物线y2=4x的焦点作直线交抛物线于A(x1,y1),B(x2,y2)两点,若x1+x2 =6,则|AB|= .?答案:85.过抛物线y2=4x的顶点O作互相垂直的两弦OM,ON,则M的横坐标x1与N的横坐标x2之积为 .?答案:16题型一抛物线简单几何性质的应用 课堂探究【例1】 已知抛物线y2=8x,
(1)求出该抛物线的顶点、焦点、准线、对称轴、变量x的范围;解:(1)抛物线y2=8x的顶点、焦点、准线、对称轴、变量x的范围分别为(0,0),(2,0),x=-2,x轴,x≥0.(2)以坐标原点O为顶点,作抛物线的内接等腰三角形OAB,|OA|=|OB|,若焦点F是△OAB的重心,求△OAB的周长.易错警示 抛物线的几何性质(对称性、范围等)在解决抛物线问题时,有着广泛的应用,但在解题过程中又容易忽视这些隐含条件,如抛物线的对称性、准线与对称轴垂直等,解题时应注意挖掘并充分利用这些隐含条件.(2)已知抛物线C的顶点在原点,焦点F在x轴正半轴上,设A,B是抛物线C上的两个动点(AB不垂直于x轴),且|AF|+|BF|=8,线段AB的垂直平分线恒经过定点Q(6,0),求此抛物线方程.题型二直线与抛物线的位置关系【例2】 已知直线l:y=k(x+1)与抛物线C:y2=4x.问:k为何值时,直线l与抛物线C有两个交点,一个交点,无交点?②若直线与抛物线有一个交点,
则k2=0或k2≠0时,Δ=0.
解得k=0或k=±1.
所以当k=0或k=±1时,直线l和抛物线C有一个交点.
③若直线与抛物线无交点,
则k2≠0且Δ<0.
解得k>1或k<-1.
所以当k>1或k<-1时,直线l和抛物线C无交点.题后反思 研究直线和抛物线的位置关系时,由于消元后所得的方程中含参数,因此要注意分二次项系数为0和不为0两种情况讨论.(2)过点(-3,2)的直线与抛物线y2=4x只有一个公共点,求此直线方程.抛物线的焦点弦问题题型三【例3】 已知直线l经过抛物线y2=6x的焦点F,且与抛物线相交于A,B两点.若直线l的倾斜角为60°,求|AB|的值.变式探究:若本例中“直线l的倾斜角为60°”改为“|AB|=9”,求线段AB的中点M到准线的距离.方法技巧 求圆锥曲线的弦长时,为简化计算常常借助根与系数的关系,这样可以避免分别求x1,x2(或y1,y2)的麻烦,如果是利用弦长求参数的问题,只需要列出参数的方程或不等式即可求解,而x1,x2(或y1,y2)一般是求不出来的.(3)以AB为直径的圆与抛物线的准线相切.题型四抛物线中的最值问题(2)在抛物线上求一点P,使P到直线x-y+3=0的距离最短,并求出距离的最小值.题后反思(2)点P在抛物线2y2=x上,点Q在圆(x-2)2+y2=1上,求|PQ|的最小值.
