高中数学新人教A版选修2-1课件:第三章空间向量与立体几何3.1.1空间向量及其加减运算3.1.2空间向量的数乘运算(41张)
文档属性
| 名称 | 高中数学新人教A版选修2-1课件:第三章空间向量与立体几何3.1.1空间向量及其加减运算3.1.2空间向量的数乘运算(41张) |  | |
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-20 19:42:07 | ||
图片预览











文档简介
课件41张PPT。3.1.1 空间向量及其加减运算
3.1.2 空间向量的数乘运算课标要求:1.经历向量及其运算由平面到空间推广的过程,了解空间向量的概念.2.掌握空间向量的加法、减法和数乘运算.3.理解空间共线向量和共面向量定理及推论.自主学习课堂探究 自主学习1.空间向量及其长度的定义
与平面向量一样,在空间,我们把 叫做空间向量,向量的大小叫做向量的长度或模.知识探究具有大小和方向的量2.空间向量的表示方法
(1)几何表示:与平面向量一样,空间向量也用 表示,有向线段的 表示向量的模.
(2)符号表示:如图所示,向量a的起点是A,终点是B,则向量a也可以记作 ,其模记为|a|或| |.空间向量在空间中是可以任
意平移的,这是向量与有向线段的本质区别.有向线段长度3.几个特殊的空间向量
(1)零向量:我们规定, 叫做零向量,记为0.当有向线段的起点A和终点B重合时 ,=0.长度为0的向量(2)单位向量: 称为单位向量.
(3)相反向量: 的向量,称为a的相反向量,记为-a.
(4)相等向量: 的向量称为相等向量,在空间,同向且等长的有向线段表示同一向量或相等向量.模为1的向量 与向量a长度相等而方向相反 方向相同且模相等注意:(1)单位向量、零向量都只是规定了向量的模长而没有规定方向,需注意单位向量有无数个,它们的方向不确定,因此,它们不一定相等;零向量也有无数个,它们的方向任意,但规定所有的零向量都相等.(2)在平面内,若以两个同向向量为对边可构成平行四边形,则这两个向量相等,在空间中,这个结论同样成立.
(3)和平面向量一样,若两个空间向量相等,则它们的方向相同,且模相等,但起点、终点未必相同.
(4)向量不能比较大小,但向量的模可以比较大小.因此,关于两个向量的比较,我们仅研究两者是否相等.4.空间向量的加减运算
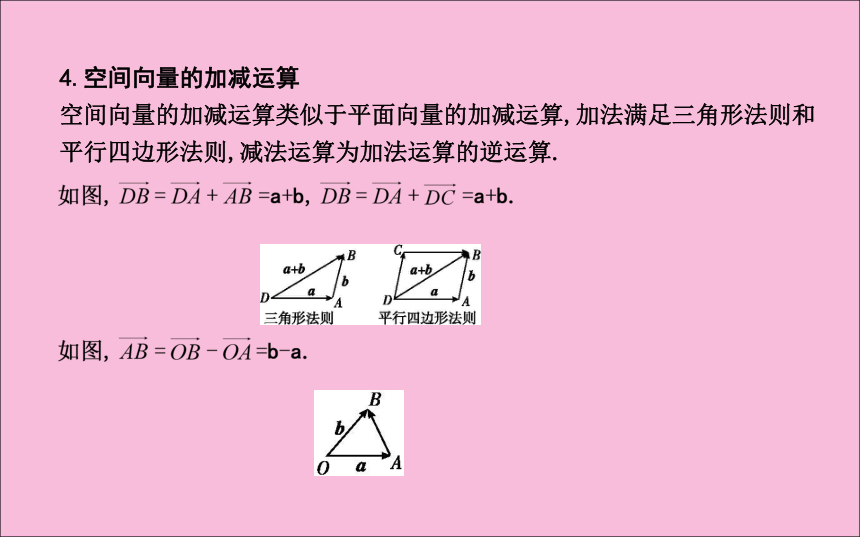
空间向量的加减运算类似于平面向量的加减运算,加法满足三角形法则和平行四边形法则,减法运算为加法运算的逆运算.5.空间向量的加法运算满足的运算律
(1)交换律:a+b=b+a;
(2)结合律:(a+b)+c=a+(b+c).6.空间向量的数乘运算的定义
(1)定义:与平面向量一样,实数λ与空间向量a的乘积λa仍然是一个向量,称为向量的数乘运算.
(2)λa的方向和长度如下:
①方向:
当λ>0时,λa与向量a方向相同,如图(1);
当λ<0时,λa与向量a方向相反,如图(2);
当λ=0时,λa=0.
②大小:
λa的长度是a的长度的|λ|倍.7.空间向量的数乘运算的运算律
(1)分配律:λ(a+b)=λa+λb;(2)结合律:λ(μa)=(λμ)a.
8.共线向量
(1)共线向量的定义
如果表示空间向量的有向线段 ,则这些向量叫做共线向量或平行向量.
理解共线向量的定义时,要注意以下两点:
①零向量和空间任一向量是共线向量.
②共线向量不具有传递性,如a∥b,b∥c,那么a∥c不一定成立,因为当b=0时,虽然a∥b,b∥c,但a不一定与c共线.所在的直线互相平行或重合(2)向量共线的充要条件(又称共线向量定理)
类似于平面向量共线的充要条件,对空间任意两个向量a,b(b≠0),a∥b的充要条件是 .
对向量共线的充要条件的理解,应从以下几个方面正确把握:
①在此充要条件中,要特别注意b≠0,若不加b≠0,则该充要性不一定成立.例如:若a≠0,b=0,则a∥b,但λ不存在,该充要性也就不成立了.②该充要条件包含两个命题:
a.a∥b?存在唯一的实数λ,使a=λb;
b.存在唯一的实数λ,使a=λb?a∥b.
③向量共线的充要条件可以作为判定线线平行的依据,但必须注意在向量a(或b)上存在一点不在向量b(或a)上.存在实数λ,使a=λb9.共面向量
(1)共面向量的定义
平行于同一个平面的向量,叫做共面向量.
空间任意两个向量必共面,但空间任意三个向量不一定共面.(2)三个向量共面的充要条件(又称共面向量定理)
如果两个向量a,b ,那么向量p与向量a,b共面的充要条件是 .不共线存在唯一的有序实数对(x,y),使p=xa+yb注意:(1)0与空间任意向量a都是共线向量.
(2)a与b共线时,表示a与b的有向线段所在直线可能是同一直线,也可能是平行直线.
(3)共线向量定理中的b≠0不可去掉,否则实数λ可能不唯一.(5)空间任意两个向量必共面,但空间任意三个向量不一定共面.
(6)空间任意直线由空间一点及直线的方向向量唯一确定.
(7)空间中任意平面由空间一点及两个不共线向量唯一确定.自我检测1.下列命题中,假命题是( )
(A)任意两个向量都是共面向量
(B)空间向量的加法运算满足交换律及结合律
(C)只有零向量的模等于0
(D)共线的单位向量都相等D解析:容易判断D是假命题,共线的单位向量是相等向量或相反向量.故
选D.C 2.空间两向量a,b互为相反向量,已知向量|b|=3,则下列结论正确的是( )
(A)a=b (B)a+b为实数0
(C)a与b方向相同 (D)|a|=3D答案:±1题型一 空间向量的有关概念 课堂探究答案:(1)D答案:(2)①②易错警示 (1)判断有关向量的命题时,要抓住向量的两个主要元素,即大小和方向,两者缺一不可.
(2)要注意零向量的特殊性.对于零向量,应明确:
①零向量不是没有方向,而是它的方向是任意的;
②零向量与任何向量都共线.
(3)对于共线向量应明确:
①当a与b共线时,表示a,b的两条有向线段所在的直线有可能是同一直线,也可能是平行直线;
②共线(平行)向量不具有传递性,如a∥b,b∥c,那么a∥c就不一定成立,因为b=0时,虽然有a∥b,b∥c,但a不一定与c共线,若a,b,c都不是零向量,则具有传递性.解析:(1)①正确,零向量的方向是任意的.
②错误,空间向量可以平行移动.
③正确,向量的模可以比较大小,有向线段长度越长,其所表示的向量的模就越大.
④错误,如果两个向量不相同,它们的长度可以相等.即时训练1-1:(1)给出下列命题:
①零向量没有确定的方向;
②空间向量是不能平行移动的;
③有向线段可用来表示空间向量,有向线段长度越长,其所表示的向量的模就越大;
④如果两个向量不相同,那么它们的长度也不相等.其中正确的是( )
(A)①② (B)②③ (C)①③ (D)①③④答案:(1)C(2)如图,在以长、宽、高分别为AB=4,AD=2,AA1=1的长方体ABCD-A1B1C1D1中的八个顶点的两点为起点和终点的向量中,单位向量共有 个,模为 的所有向量为 .?题型二 空间向量的加减和数乘运算答案:(2)①②③④ (1)利用向量的加减运算是处理此类问题的基本方法,一般地,可以找到的封闭图形不是唯一的,但无论哪一种途径,结果应是唯一的.
(2)应用向量的加减法法则和数乘运算表示向量是向量在几何中应用的前提,一定要熟练掌握.方法技巧答案:(1)b-a+c a+b-c 空间向量共线问题题型三方法技巧 (1)判断向量共线的策略
①熟记共线向量充要条件:a∥b,b≠0,则存在惟一实数λ使a=λb;若存在惟一实数λ,使a=λb,则a∥b.
②判断向量共线的关键:找到实数λ.
(2)三点共线与直线平行的判断
①线线平行:证明两直线平行要先证明两直线的方向向量a,b平行,还要证明一直线上有一点不在另一条直线上.题型四 空间向量共面问题(1)证明:A,E,C1,F四点共面;方法技巧 (1)证明空间三个向量共面,常用如下方法:
①设法证明其中一个向量可以表示成另两个向量的线性组合,即若a=xb+yc,则向量a,b,c共面;
②寻找平面α,证明这些向量与平面α平行.
3.1.2 空间向量的数乘运算课标要求:1.经历向量及其运算由平面到空间推广的过程,了解空间向量的概念.2.掌握空间向量的加法、减法和数乘运算.3.理解空间共线向量和共面向量定理及推论.自主学习课堂探究 自主学习1.空间向量及其长度的定义
与平面向量一样,在空间,我们把 叫做空间向量,向量的大小叫做向量的长度或模.知识探究具有大小和方向的量2.空间向量的表示方法
(1)几何表示:与平面向量一样,空间向量也用 表示,有向线段的 表示向量的模.
(2)符号表示:如图所示,向量a的起点是A,终点是B,则向量a也可以记作 ,其模记为|a|或| |.空间向量在空间中是可以任
意平移的,这是向量与有向线段的本质区别.有向线段长度3.几个特殊的空间向量
(1)零向量:我们规定, 叫做零向量,记为0.当有向线段的起点A和终点B重合时 ,=0.长度为0的向量(2)单位向量: 称为单位向量.
(3)相反向量: 的向量,称为a的相反向量,记为-a.
(4)相等向量: 的向量称为相等向量,在空间,同向且等长的有向线段表示同一向量或相等向量.模为1的向量 与向量a长度相等而方向相反 方向相同且模相等注意:(1)单位向量、零向量都只是规定了向量的模长而没有规定方向,需注意单位向量有无数个,它们的方向不确定,因此,它们不一定相等;零向量也有无数个,它们的方向任意,但规定所有的零向量都相等.(2)在平面内,若以两个同向向量为对边可构成平行四边形,则这两个向量相等,在空间中,这个结论同样成立.
(3)和平面向量一样,若两个空间向量相等,则它们的方向相同,且模相等,但起点、终点未必相同.
(4)向量不能比较大小,但向量的模可以比较大小.因此,关于两个向量的比较,我们仅研究两者是否相等.4.空间向量的加减运算
空间向量的加减运算类似于平面向量的加减运算,加法满足三角形法则和平行四边形法则,减法运算为加法运算的逆运算.5.空间向量的加法运算满足的运算律
(1)交换律:a+b=b+a;
(2)结合律:(a+b)+c=a+(b+c).6.空间向量的数乘运算的定义
(1)定义:与平面向量一样,实数λ与空间向量a的乘积λa仍然是一个向量,称为向量的数乘运算.
(2)λa的方向和长度如下:
①方向:
当λ>0时,λa与向量a方向相同,如图(1);
当λ<0时,λa与向量a方向相反,如图(2);
当λ=0时,λa=0.
②大小:
λa的长度是a的长度的|λ|倍.7.空间向量的数乘运算的运算律
(1)分配律:λ(a+b)=λa+λb;(2)结合律:λ(μa)=(λμ)a.
8.共线向量
(1)共线向量的定义
如果表示空间向量的有向线段 ,则这些向量叫做共线向量或平行向量.
理解共线向量的定义时,要注意以下两点:
①零向量和空间任一向量是共线向量.
②共线向量不具有传递性,如a∥b,b∥c,那么a∥c不一定成立,因为当b=0时,虽然a∥b,b∥c,但a不一定与c共线.所在的直线互相平行或重合(2)向量共线的充要条件(又称共线向量定理)
类似于平面向量共线的充要条件,对空间任意两个向量a,b(b≠0),a∥b的充要条件是 .
对向量共线的充要条件的理解,应从以下几个方面正确把握:
①在此充要条件中,要特别注意b≠0,若不加b≠0,则该充要性不一定成立.例如:若a≠0,b=0,则a∥b,但λ不存在,该充要性也就不成立了.②该充要条件包含两个命题:
a.a∥b?存在唯一的实数λ,使a=λb;
b.存在唯一的实数λ,使a=λb?a∥b.
③向量共线的充要条件可以作为判定线线平行的依据,但必须注意在向量a(或b)上存在一点不在向量b(或a)上.存在实数λ,使a=λb9.共面向量
(1)共面向量的定义
平行于同一个平面的向量,叫做共面向量.
空间任意两个向量必共面,但空间任意三个向量不一定共面.(2)三个向量共面的充要条件(又称共面向量定理)
如果两个向量a,b ,那么向量p与向量a,b共面的充要条件是 .不共线存在唯一的有序实数对(x,y),使p=xa+yb注意:(1)0与空间任意向量a都是共线向量.
(2)a与b共线时,表示a与b的有向线段所在直线可能是同一直线,也可能是平行直线.
(3)共线向量定理中的b≠0不可去掉,否则实数λ可能不唯一.(5)空间任意两个向量必共面,但空间任意三个向量不一定共面.
(6)空间任意直线由空间一点及直线的方向向量唯一确定.
(7)空间中任意平面由空间一点及两个不共线向量唯一确定.自我检测1.下列命题中,假命题是( )
(A)任意两个向量都是共面向量
(B)空间向量的加法运算满足交换律及结合律
(C)只有零向量的模等于0
(D)共线的单位向量都相等D解析:容易判断D是假命题,共线的单位向量是相等向量或相反向量.故
选D.C 2.空间两向量a,b互为相反向量,已知向量|b|=3,则下列结论正确的是( )
(A)a=b (B)a+b为实数0
(C)a与b方向相同 (D)|a|=3D答案:±1题型一 空间向量的有关概念 课堂探究答案:(1)D答案:(2)①②易错警示 (1)判断有关向量的命题时,要抓住向量的两个主要元素,即大小和方向,两者缺一不可.
(2)要注意零向量的特殊性.对于零向量,应明确:
①零向量不是没有方向,而是它的方向是任意的;
②零向量与任何向量都共线.
(3)对于共线向量应明确:
①当a与b共线时,表示a,b的两条有向线段所在的直线有可能是同一直线,也可能是平行直线;
②共线(平行)向量不具有传递性,如a∥b,b∥c,那么a∥c就不一定成立,因为b=0时,虽然有a∥b,b∥c,但a不一定与c共线,若a,b,c都不是零向量,则具有传递性.解析:(1)①正确,零向量的方向是任意的.
②错误,空间向量可以平行移动.
③正确,向量的模可以比较大小,有向线段长度越长,其所表示的向量的模就越大.
④错误,如果两个向量不相同,它们的长度可以相等.即时训练1-1:(1)给出下列命题:
①零向量没有确定的方向;
②空间向量是不能平行移动的;
③有向线段可用来表示空间向量,有向线段长度越长,其所表示的向量的模就越大;
④如果两个向量不相同,那么它们的长度也不相等.其中正确的是( )
(A)①② (B)②③ (C)①③ (D)①③④答案:(1)C(2)如图,在以长、宽、高分别为AB=4,AD=2,AA1=1的长方体ABCD-A1B1C1D1中的八个顶点的两点为起点和终点的向量中,单位向量共有 个,模为 的所有向量为 .?题型二 空间向量的加减和数乘运算答案:(2)①②③④ (1)利用向量的加减运算是处理此类问题的基本方法,一般地,可以找到的封闭图形不是唯一的,但无论哪一种途径,结果应是唯一的.
(2)应用向量的加减法法则和数乘运算表示向量是向量在几何中应用的前提,一定要熟练掌握.方法技巧答案:(1)b-a+c a+b-c 空间向量共线问题题型三方法技巧 (1)判断向量共线的策略
①熟记共线向量充要条件:a∥b,b≠0,则存在惟一实数λ使a=λb;若存在惟一实数λ,使a=λb,则a∥b.
②判断向量共线的关键:找到实数λ.
(2)三点共线与直线平行的判断
①线线平行:证明两直线平行要先证明两直线的方向向量a,b平行,还要证明一直线上有一点不在另一条直线上.题型四 空间向量共面问题(1)证明:A,E,C1,F四点共面;方法技巧 (1)证明空间三个向量共面,常用如下方法:
①设法证明其中一个向量可以表示成另两个向量的线性组合,即若a=xb+yc,则向量a,b,c共面;
②寻找平面α,证明这些向量与平面α平行.
