高中数学新人教A版选修2-1课件:第三章空间向量与立体几何3.1.3空间向量的数量积运算(30张)
文档属性
| 名称 | 高中数学新人教A版选修2-1课件:第三章空间向量与立体几何3.1.3空间向量的数量积运算(30张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-20 00:00:00 | ||
图片预览











文档简介
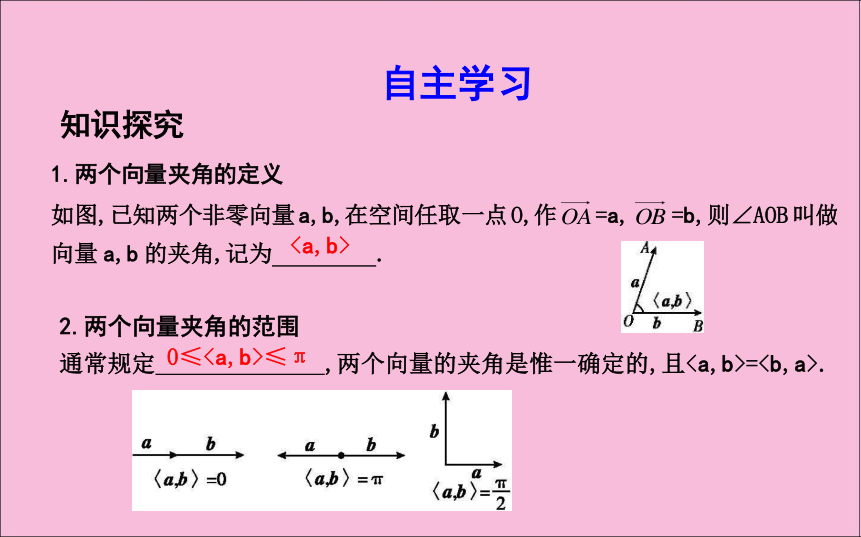
课件30张PPT。3.1.3 空间向量的数量积运算课标要求:1.掌握空间向量夹角的概念及表示方法,掌握两个向量的数量积的概念、性质和计算方法及运算律.2.掌握两个向量的数量积的主要用途,会用它解决立体几何中一些简单的问题. 自主学习知识探究2.两个向量夹角的范围
通常规定 ,两个向量的夹角是惟一确定的,且=.0≤≤π特点地,如图.
当=0时,向量a,b ;
当=π时,向量a,b ;
当= 时,向量a,b互相垂直,记作a⊥b.同向共线反向共线注意:对空间两个向量夹角的理解,应注意以下几点:
(1)两个非零向量才有夹角,当两非零向量同向时,夹角为0;反向时,夹角为π.故=0或π?a∥b(a,b为非零向量).(2)零向量与其他向量之间不定义夹角,并约定0与任何向量a都是共线的,即0∥a.(3)对空间任意两个向量a,b,有:
①==<-a,-b>=<-b,-a>;②=<-a,b>=π-;3.空间向量的数量积的定义及几何意义
已知两个非零向量a,b,则|a||b|cos叫做a,b的数量积,记作a·b,即
.零向量与任何向量的数量积为0.类比平面向量,我们可得a·b的几何意义 :数量积a·b等于a的长度|a|与b在a的方向上的投影|b|cos的乘积,或b的长度|b|与a在b的方向上的投影|a|cos的乘积.4.空间向量数量积的性质
(1)若a是非零向量,e是任意单位向量,则a·e=|a|cos.
(2)若a,b是非零向量,则a⊥b?a·b=0.
(3)a·a=|a||a|cos=|a|2.
(4)若θ为a与b的夹角,则cos θ= .a·b=|a||b|·cos5.空间向量数量积的运算律
(1)(λa)·b=λ(a·b);
(2)a·b=b·a(交换律);
(3)a·(b+c)=a·b+a·c(分配律).注意:对于空间向量的数量积, 我们可以从以下几个方面理解:(1)向量a, b的数量积记为a·b,而不能表示为a×b或ab.
(2)向量的数量积的结果为实数,而不是向量,其符号由夹角θ的余弦值的符号决定.当θ为锐角时,a·b>0,但当a·b>0时,θ不一定是锐角,因为θ也可能为0;当θ为钝角时,a·b<0,但当a·b<0时,θ不一定是钝角,因为θ也可能为π.(3)对于任意一个非零向量a,我们把 叫做向量a的单位向量,记作a0,a0与a同方向.(4)当a≠0时,由a·b=0不能推出b一定是零向量,这是因为对于任意一个与a垂直的非零向量b,都有a·b=0.自我检测1.已知a,b均为单位向量,它们的夹角为60°,那么|a+3b|等于( )CC3.已知空间四边形ABCD中,∠ACD=∠BDC=90°,且AB=2,CD=1,则AB与CD所成
的角是( )
(A)30° (B)45°
(C)60° (D)90°C解析:(a+3c)·(3b-2a)=3a·b-2|a|2+9b·c-6a·c=-62.
答案:-624.设向量a与b互相垂直,向量c与它们构成的角是60°,且|a|=5,|b|=3, |c|=8,则(a+3c)·(3b-2a)= .?题型一空间向量数量积的运算 课堂探究【例1】 已知长方体ABCD-A1B1C1D1中,AB=AA1=2,AD=4,E为侧面AA1B1B的中心,F为A1D1的中点.
求下列向量的数量积.即时训练1-1:如图,已知空间四边形ABCD的每条边和对角线长都等于a,点E,F,G分别是AB,AD,DC的中点,求下列向量的数量积:题型二 利用空间向量的数量积求夹角方法技巧 (1)求几何体中两个向量的夹角可以把其中一个向量平移使其起点与另一个向量的起点重合,通过解三角形得出夹角的大小,此法就是求两个向量夹角的平移法.(2)由两个向量的数量积定义得cos= ,求的大小,转化为求两个向量的数量积及两个向量的模的大小,求出的余弦值,进而求的大小.
(3)利用向量的数量积求出两向量的夹角,则这个夹角就是两异面直线所成的角或补角(注意异面直线所成角的范围).即时训练2-1:如图所示,在棱长为a的正方体ABCD-A1B1C1D1中,求异面直线BA1与AC所成的角.利用空间向量解决垂直问题题型三【例3】 如图,已知平行六面体ABCD-A1B1C1D1的底面ABCD是菱形,且∠C1CB =∠C1CD=∠BCD.求证:CA1⊥B1D1.方法技巧 用向量法证明垂直关系的操作步骤
(1)把几何问题转化为向量问题;(2)用已知向量表示所证向量;(3)结合数量积公式和运算律证明数量积为0;(4)将向量问题回归到几何问题.即时训练3-1:已知空间四边形OABC中,∠AOB=∠BOC=∠AOC,且OA=OB=OC. M,N分别是OA,BC的中点,G是MN的中点.求证:OG⊥BC.题型四 利用数量积求距离【例4】 如图1所示,在平行四边形ABCD中,AB=AC=1,∠ACD =90°,将它沿对角线AC折起,使AB与CD成60°角,如图2所示,求B,D间的距离.题后反思 用空间向量求两点间距离,首先用其他已知夹角和模的向量表示此向量,再利用a·a=|a|2,通过向量运算求|a|.即时训练4-1:如图所示,在空间四边形OABC中,OA,OB,OC两两成60°角,且OA=OB=OC=2,E为OA的中点,F为BC的中点,试求E,F间的距离.
通常规定 ,两个向量的夹角是惟一确定的,且
当
当
当
(1)两个非零向量才有夹角,当两非零向量同向时,夹角为0;反向时,夹角为π.故
①
已知两个非零向量a,b,则|a||b|cos
.零向量与任何向量的数量积为0.类比平面向量,我们可得a·b的几何意义 :数量积a·b等于a的长度|a|与b在a的方向上的投影|b|cos
(1)若a是非零向量,e是任意单位向量,则a·e=|a|cos
(2)若a,b是非零向量,则a⊥b?a·b=0.
(3)a·a=|a||a|cos
(4)若θ为a与b的夹角,则cos θ= .a·b=|a||b|·cos
(1)(λa)·b=λ(a·b);
(2)a·b=b·a(交换律);
(3)a·(b+c)=a·b+a·c(分配律).注意:对于空间向量的数量积, 我们可以从以下几个方面理解:(1)向量a, b的数量积记为a·b,而不能表示为a×b或ab.
(2)向量的数量积的结果为实数,而不是向量,其符号由夹角θ的余弦值的符号决定.当θ为锐角时,a·b>0,但当a·b>0时,θ不一定是锐角,因为θ也可能为0;当θ为钝角时,a·b<0,但当a·b<0时,θ不一定是钝角,因为θ也可能为π.(3)对于任意一个非零向量a,我们把 叫做向量a的单位向量,记作a0,a0与a同方向.(4)当a≠0时,由a·b=0不能推出b一定是零向量,这是因为对于任意一个与a垂直的非零向量b,都有a·b=0.自我检测1.已知a,b均为单位向量,它们的夹角为60°,那么|a+3b|等于( )CC3.已知空间四边形ABCD中,∠ACD=∠BDC=90°,且AB=2,CD=1,则AB与CD所成
的角是( )
(A)30° (B)45°
(C)60° (D)90°C解析:(a+3c)·(3b-2a)=3a·b-2|a|2+9b·c-6a·c=-62.
答案:-624.设向量a与b互相垂直,向量c与它们构成的角是60°,且|a|=5,|b|=3, |c|=8,则(a+3c)·(3b-2a)= .?题型一空间向量数量积的运算 课堂探究【例1】 已知长方体ABCD-A1B1C1D1中,AB=AA1=2,AD=4,E为侧面AA1B1B的中心,F为A1D1的中点.
求下列向量的数量积.即时训练1-1:如图,已知空间四边形ABCD的每条边和对角线长都等于a,点E,F,G分别是AB,AD,DC的中点,求下列向量的数量积:题型二 利用空间向量的数量积求夹角方法技巧 (1)求几何体中两个向量的夹角可以把其中一个向量平移使其起点与另一个向量的起点重合,通过解三角形得出夹角的大小,此法就是求两个向量夹角的平移法.(2)由两个向量的数量积定义得cos
(3)利用向量的数量积求出两向量的夹角,则这个夹角就是两异面直线所成的角或补角(注意异面直线所成角的范围).即时训练2-1:如图所示,在棱长为a的正方体ABCD-A1B1C1D1中,求异面直线BA1与AC所成的角.利用空间向量解决垂直问题题型三【例3】 如图,已知平行六面体ABCD-A1B1C1D1的底面ABCD是菱形,且∠C1CB =∠C1CD=∠BCD.求证:CA1⊥B1D1.方法技巧 用向量法证明垂直关系的操作步骤
(1)把几何问题转化为向量问题;(2)用已知向量表示所证向量;(3)结合数量积公式和运算律证明数量积为0;(4)将向量问题回归到几何问题.即时训练3-1:已知空间四边形OABC中,∠AOB=∠BOC=∠AOC,且OA=OB=OC. M,N分别是OA,BC的中点,G是MN的中点.求证:OG⊥BC.题型四 利用数量积求距离【例4】 如图1所示,在平行四边形ABCD中,AB=AC=1,∠ACD =90°,将它沿对角线AC折起,使AB与CD成60°角,如图2所示,求B,D间的距离.题后反思 用空间向量求两点间距离,首先用其他已知夹角和模的向量表示此向量,再利用a·a=|a|2,通过向量运算求|a|.即时训练4-1:如图所示,在空间四边形OABC中,OA,OB,OC两两成60°角,且OA=OB=OC=2,E为OA的中点,F为BC的中点,试求E,F间的距离.
