高中数学新人教A版选修2-1课件:第三章空间向量与立体几何3.2立体几何中的向量方法第一课时空间向量与平行、垂直关系(44张)
文档属性
| 名称 | 高中数学新人教A版选修2-1课件:第三章空间向量与立体几何3.2立体几何中的向量方法第一课时空间向量与平行、垂直关系(44张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-20 19:43:28 | ||
图片预览










文档简介
课件44张PPT。第一课时 空间向量与平行、垂直关系课标要求:1.理解直线的方向向量与平面的法向量,并能运用它们证明平行问题和垂直问题.2.能用向量语言表述线线、线面、面面的平行关系和垂直关系. 自主学习知识探究1.点的位置向量3.空间平面的向量表示4.平面法向量的定义
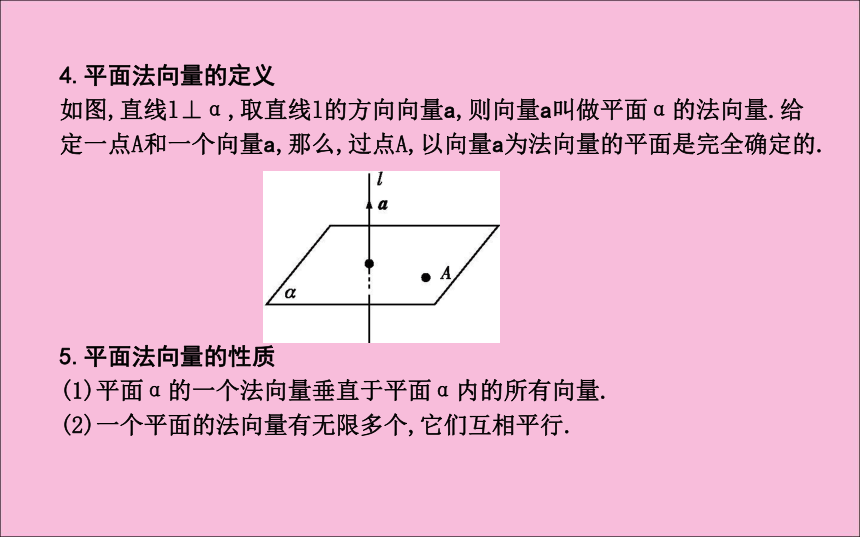
如图,直线l⊥α,取直线l的方向向量a,则向量a叫做平面α的法向量.给定一点A和一个向量a,那么,过点A,以向量a为法向量的平面是完全确定的.5.平面法向量的性质
(1)平面α的一个法向量垂直于平面α内的所有向量.
(2)一个平面的法向量有无限多个,它们互相平行.6.平面的法向量的求法
已知平面内两条相交直线的方向向量,可求出该平面的一个法向量.
确定平面的法向量通常有两种方法:
方法一:在几何体中已经给出有向线段,只需证明线面垂直.
方法二:在几何体中没有现成的有向线段,这时一般要建立空间直角坐标系,然后用待定系数法求平面的法向量.一般步骤如下:
(1)设平面的一个法向量为n=(x,y,z).
(2)找出(求出)平面内的两个不共线的向量的坐标:a=(a1,b1,c1),b=(a2, b2,c2).(3)根据法向量的定义建立关于x,y,z的方程组:(4)解方程组,取其中的一组解,即得该平面的一个法向量.由于平面的法向量有无数个,故可在方程组的解中取一个较简单的作为平面的法向量.7.利用空间向量表示立体几何中的平行与垂直关系
因为直线的方向向量与平面的法向量可以确定直线与平面的位置关系,所以我们可以利用直线的方向向量与平面的法向量来研究空间直线、平面的平行(或垂直)问题.
设直线l,m的方向向量分别为a,b,平面α,β的法向量分别为u,v,则①线线平行:l∥m?a∥b?a=kb,k∈R;
线面平行:l∥α?a⊥u且l?α?a·u=0且l?α;
面面平行:α∥β?u∥v?u=kv,k∈R.②线线垂直:l⊥m?a⊥b?a·b=0;
线面垂直:l⊥α?a∥u?a=ku,k∈R;
面面垂直:α⊥β?u⊥v?u·v=0.8.用向量法证明空间中的平行关系
空间中的平行关系有:直线与直线平行、直线与平面平行、平面与平面平行.
(1)线线平行
设直线l1,l2的方向向量分别为v1=(a1,b1,c1),v2=(a2,b2,c2),则l1∥l2?v1∥v2?v1=λv2(λ∈R)?a1=λa2,b1=λb2,c1=λc2.(2)线面平行
证法一:设直线l的方向向量是a=(x1,y1,z1),平面α的法向量是u=(x2,y2, z2),则l∥α?a⊥u,且l?α?a·u=0且l?α?x1x2+y1y2+z1z2=0且l?α.
证法二:根据线面平行的判定定理“如果直线(平面外)与平面内的一条直线平行,那么这条直线和这个平面平行”,要证明一条直线和一个平面平行,可以在平面内找一个向量与已知直线的方向向量是共线向量即可.
证法三:根据共面向量定理可知,如果一个向量和两个不共线的向量是共面向量,那么这个向量与这两个不共线向量确定的平面必定平行,因此要证明一条直线和一个平面平行,只要证明这条直线的方向向量能够用平面内两个不共线的向量线性表示即可.(3)面面平行
证法一:由面面平行的判定定理知,要证明面面平行,只要转化为证明相应的线面平行、线线平行即可.
证法二:若能求出平面α,β的法向量u,v,要证明α∥β,只要证明u∥v即可.9.用向量法证明空间中的垂直关系
空间中的垂直关系有:线线垂直、线面垂直、面面垂直.
(1)线线垂直
设直线l1,l2的方向向量分别为a1,a2,要证明l1⊥l2,只要证明a1·a2=0即可.
(2)线面垂直
证法一:设直线l的方向向量为a,平面α的法向量为u,要证l⊥α,只要证a∥u即可.
证法二:根据线面垂直的判定定理,转化为证明直线的方向向量与平面内两个不共线的向量垂直.
(3)面面垂直
设平面α,β的法向量分别为u1,u2,则只需证明u1⊥u2,即只需证明u1·u2=0即可.自我检测1.已知A(1,2,3),B(2,1,4)是直线AB上两点,单位向量e是直线AB的方向向量,则e等于( )C解析:问题即求与n共线的一个向量.即n=(2,-3,1)=-(-2,3,-1).2.若n=(2,-3,1)是平面α的一个法向量,则下列向量中能作为平面α的法向量的是( )
(A)(0,-3,1) (B)(2,0,1)
(C)(-2,-3,1) (D)(-2,3,-1)D3.已知直线l与平面α垂直,直线l的一个方向向量为u=(1,-3,z),向量v=(3,-2,1)与平面α平行,则z等于( )
(A)3 (B)6
(C)-9 (D)9C解析:因为l⊥α,v与平面α平行,所以u⊥v,即u·v=0,所以1×3+3×2+z×1=0,
所以z=-9.答案:-84.已知直线l的方向向量为(2,m,1),平面α的法向量为(1, ,2),且l∥α,则m= .?答案:-105.若平面α,β的法向量分别为(-1,2,4),(x,-1,-2),并且α⊥β,则x的值为 .?题型一 求平面的法向量 课堂探究【例1】 如图所示,在四棱锥S-ABCD中,底面是直角梯形,∠ABC=90°, SA⊥底面ABCD,且SA=AB=BC=1,AD= ,建立适当的空间直角坐标系,求平面SCD与平面SBA的一个法向量.方法技巧 求平面法向量的方法与步骤(2)设平面的法向量为n=(x,y,z);(4)所求出向量中的三个坐标不是具体的值而是比例关系,设定一个坐标为常数(常数不能为0)便可得到平面的一个法向量.即时训练1-1:已知A(1,0,1),B(0,1,1),C(1,1,0),求平面ABC的一个法
向量.题型二利用空间向量证明平行问题【例2】 已知正方体ABCD-A1B1C1D1的棱长为2,E,F分别是BB1,DD1的中点,求证:FC1∥平面ADE.变式探究:在本例条件下,求证:平面ADE∥平面B1C1F.方法技巧 利用向量法证明几何中的平行问题可以通过两条途径实现,一是利用三角形法则和平面向量基本定理实现向量间的相互转化,得到向量的共线关系;二是通过建立空间直角坐标系,借助直线的方向向量和平面的法向量进行平行关系的证明.即时训练2-1:如图所示,在正方体ABCD-A1B1C1D1中,M,N分别是C1C,B1C1的中点.求证:MN∥平面A1BD.证明:法一 如图所示,以D为原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,
题型三 利用空间向量证明线线垂直方法技巧 用向量法证明空间两条直线相互垂直,主要思路是证明两直线的方向向量相互垂直,具体方法为
(1)坐标法:根据图形的特征,建立恰当的直角坐标系,准确地写出相关点的坐标,表达出两直线的方向向量,证明其数量积为0.
(2)基向量法:利用向量的加减法运算,结合图形,将要证明的两直线所在的向量用基向量表达出来,利用数量积运算证明两向量的数量积为0.即时训练3-1:在棱长为a的正方体ABCD-A1B1C1D1中,E,F分别是AB,BC的中点,求证:A1F⊥C1E.题型四 利用空间向量证明线面垂直问题(1)设平面PAB∩平面PCD=m,求证:CD∥m;证明:(1)因为AB∥CD,
CD?平面PAB,AB?平面PAB,
所以CD∥平面PAB.
因为CD?平面PCD,平面PAB∩平面PCD=m,
所以CD∥m.(2)证明:BD⊥平面PAC.方法技巧 用向量法证明线面垂直的方法及步骤
(1)基向量法
①确定基向量作为空间的一个基底,用基向量表示有关直线的方向向量;
②找出平面内两条相交直线的方向向量,并分别用基向量表示;
③分别计算有关直线的方向向量与平面内相交直线的方向向量的数量积,根据数量积为0,证得线线垂直,然后由线面垂直的判定定理得出结论.
(2)坐标法
方法一:①建立空间直角坐标系;
②将直线的方向向量用坐标表示;
③找出平面内两条相交直线,并用坐标表示它们的方向向量;
④分别计算两组向量的数量积,得到数量积为0.
方法二:①建立空间直角坐标系;
②将直线的方向向量用坐标表示;
③找出平面的法向量;
④判断直线的方向向量与平面的法向量平行.即时训练4-1:如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,A1O⊥平面ABCD,AB=AA1= .
证明:A1C⊥平面BB1D1D.题型五 利用空间向量证明面面垂直问题【例5】 如图,正四棱柱ABCD-A1B1C1D1中,底面边长为2 ,侧棱长为4,E, F分别是棱AB,BC的中点,EF∩BD=G.求证:平面B1EF⊥平面BDD1B1.证明:以D为原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系,
由题意知方法技巧 利用空间向量证明面面垂直通常可以有两个途径,一是利用两个平面垂直的判定定理将面面垂直问题转化为线面垂直进而转化为线线垂直;二是直接求解两个平面的法向量,证明两个法向量垂直,从而得到两个平面垂直.即时训练5-1:如图所示,在直三棱柱ABC-A1B1C1中,AB⊥BC,AB=BC=2,BB1= 1,E为BB1的中点,证明:平面AEC1⊥平面AA1C1C.
如图,直线l⊥α,取直线l的方向向量a,则向量a叫做平面α的法向量.给定一点A和一个向量a,那么,过点A,以向量a为法向量的平面是完全确定的.5.平面法向量的性质
(1)平面α的一个法向量垂直于平面α内的所有向量.
(2)一个平面的法向量有无限多个,它们互相平行.6.平面的法向量的求法
已知平面内两条相交直线的方向向量,可求出该平面的一个法向量.
确定平面的法向量通常有两种方法:
方法一:在几何体中已经给出有向线段,只需证明线面垂直.
方法二:在几何体中没有现成的有向线段,这时一般要建立空间直角坐标系,然后用待定系数法求平面的法向量.一般步骤如下:
(1)设平面的一个法向量为n=(x,y,z).
(2)找出(求出)平面内的两个不共线的向量的坐标:a=(a1,b1,c1),b=(a2, b2,c2).(3)根据法向量的定义建立关于x,y,z的方程组:(4)解方程组,取其中的一组解,即得该平面的一个法向量.由于平面的法向量有无数个,故可在方程组的解中取一个较简单的作为平面的法向量.7.利用空间向量表示立体几何中的平行与垂直关系
因为直线的方向向量与平面的法向量可以确定直线与平面的位置关系,所以我们可以利用直线的方向向量与平面的法向量来研究空间直线、平面的平行(或垂直)问题.
设直线l,m的方向向量分别为a,b,平面α,β的法向量分别为u,v,则①线线平行:l∥m?a∥b?a=kb,k∈R;
线面平行:l∥α?a⊥u且l?α?a·u=0且l?α;
面面平行:α∥β?u∥v?u=kv,k∈R.②线线垂直:l⊥m?a⊥b?a·b=0;
线面垂直:l⊥α?a∥u?a=ku,k∈R;
面面垂直:α⊥β?u⊥v?u·v=0.8.用向量法证明空间中的平行关系
空间中的平行关系有:直线与直线平行、直线与平面平行、平面与平面平行.
(1)线线平行
设直线l1,l2的方向向量分别为v1=(a1,b1,c1),v2=(a2,b2,c2),则l1∥l2?v1∥v2?v1=λv2(λ∈R)?a1=λa2,b1=λb2,c1=λc2.(2)线面平行
证法一:设直线l的方向向量是a=(x1,y1,z1),平面α的法向量是u=(x2,y2, z2),则l∥α?a⊥u,且l?α?a·u=0且l?α?x1x2+y1y2+z1z2=0且l?α.
证法二:根据线面平行的判定定理“如果直线(平面外)与平面内的一条直线平行,那么这条直线和这个平面平行”,要证明一条直线和一个平面平行,可以在平面内找一个向量与已知直线的方向向量是共线向量即可.
证法三:根据共面向量定理可知,如果一个向量和两个不共线的向量是共面向量,那么这个向量与这两个不共线向量确定的平面必定平行,因此要证明一条直线和一个平面平行,只要证明这条直线的方向向量能够用平面内两个不共线的向量线性表示即可.(3)面面平行
证法一:由面面平行的判定定理知,要证明面面平行,只要转化为证明相应的线面平行、线线平行即可.
证法二:若能求出平面α,β的法向量u,v,要证明α∥β,只要证明u∥v即可.9.用向量法证明空间中的垂直关系
空间中的垂直关系有:线线垂直、线面垂直、面面垂直.
(1)线线垂直
设直线l1,l2的方向向量分别为a1,a2,要证明l1⊥l2,只要证明a1·a2=0即可.
(2)线面垂直
证法一:设直线l的方向向量为a,平面α的法向量为u,要证l⊥α,只要证a∥u即可.
证法二:根据线面垂直的判定定理,转化为证明直线的方向向量与平面内两个不共线的向量垂直.
(3)面面垂直
设平面α,β的法向量分别为u1,u2,则只需证明u1⊥u2,即只需证明u1·u2=0即可.自我检测1.已知A(1,2,3),B(2,1,4)是直线AB上两点,单位向量e是直线AB的方向向量,则e等于( )C解析:问题即求与n共线的一个向量.即n=(2,-3,1)=-(-2,3,-1).2.若n=(2,-3,1)是平面α的一个法向量,则下列向量中能作为平面α的法向量的是( )
(A)(0,-3,1) (B)(2,0,1)
(C)(-2,-3,1) (D)(-2,3,-1)D3.已知直线l与平面α垂直,直线l的一个方向向量为u=(1,-3,z),向量v=(3,-2,1)与平面α平行,则z等于( )
(A)3 (B)6
(C)-9 (D)9C解析:因为l⊥α,v与平面α平行,所以u⊥v,即u·v=0,所以1×3+3×2+z×1=0,
所以z=-9.答案:-84.已知直线l的方向向量为(2,m,1),平面α的法向量为(1, ,2),且l∥α,则m= .?答案:-105.若平面α,β的法向量分别为(-1,2,4),(x,-1,-2),并且α⊥β,则x的值为 .?题型一 求平面的法向量 课堂探究【例1】 如图所示,在四棱锥S-ABCD中,底面是直角梯形,∠ABC=90°, SA⊥底面ABCD,且SA=AB=BC=1,AD= ,建立适当的空间直角坐标系,求平面SCD与平面SBA的一个法向量.方法技巧 求平面法向量的方法与步骤(2)设平面的法向量为n=(x,y,z);(4)所求出向量中的三个坐标不是具体的值而是比例关系,设定一个坐标为常数(常数不能为0)便可得到平面的一个法向量.即时训练1-1:已知A(1,0,1),B(0,1,1),C(1,1,0),求平面ABC的一个法
向量.题型二利用空间向量证明平行问题【例2】 已知正方体ABCD-A1B1C1D1的棱长为2,E,F分别是BB1,DD1的中点,求证:FC1∥平面ADE.变式探究:在本例条件下,求证:平面ADE∥平面B1C1F.方法技巧 利用向量法证明几何中的平行问题可以通过两条途径实现,一是利用三角形法则和平面向量基本定理实现向量间的相互转化,得到向量的共线关系;二是通过建立空间直角坐标系,借助直线的方向向量和平面的法向量进行平行关系的证明.即时训练2-1:如图所示,在正方体ABCD-A1B1C1D1中,M,N分别是C1C,B1C1的中点.求证:MN∥平面A1BD.证明:法一 如图所示,以D为原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,
题型三 利用空间向量证明线线垂直方法技巧 用向量法证明空间两条直线相互垂直,主要思路是证明两直线的方向向量相互垂直,具体方法为
(1)坐标法:根据图形的特征,建立恰当的直角坐标系,准确地写出相关点的坐标,表达出两直线的方向向量,证明其数量积为0.
(2)基向量法:利用向量的加减法运算,结合图形,将要证明的两直线所在的向量用基向量表达出来,利用数量积运算证明两向量的数量积为0.即时训练3-1:在棱长为a的正方体ABCD-A1B1C1D1中,E,F分别是AB,BC的中点,求证:A1F⊥C1E.题型四 利用空间向量证明线面垂直问题(1)设平面PAB∩平面PCD=m,求证:CD∥m;证明:(1)因为AB∥CD,
CD?平面PAB,AB?平面PAB,
所以CD∥平面PAB.
因为CD?平面PCD,平面PAB∩平面PCD=m,
所以CD∥m.(2)证明:BD⊥平面PAC.方法技巧 用向量法证明线面垂直的方法及步骤
(1)基向量法
①确定基向量作为空间的一个基底,用基向量表示有关直线的方向向量;
②找出平面内两条相交直线的方向向量,并分别用基向量表示;
③分别计算有关直线的方向向量与平面内相交直线的方向向量的数量积,根据数量积为0,证得线线垂直,然后由线面垂直的判定定理得出结论.
(2)坐标法
方法一:①建立空间直角坐标系;
②将直线的方向向量用坐标表示;
③找出平面内两条相交直线,并用坐标表示它们的方向向量;
④分别计算两组向量的数量积,得到数量积为0.
方法二:①建立空间直角坐标系;
②将直线的方向向量用坐标表示;
③找出平面的法向量;
④判断直线的方向向量与平面的法向量平行.即时训练4-1:如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,A1O⊥平面ABCD,AB=AA1= .
证明:A1C⊥平面BB1D1D.题型五 利用空间向量证明面面垂直问题【例5】 如图,正四棱柱ABCD-A1B1C1D1中,底面边长为2 ,侧棱长为4,E, F分别是棱AB,BC的中点,EF∩BD=G.求证:平面B1EF⊥平面BDD1B1.证明:以D为原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系,
由题意知方法技巧 利用空间向量证明面面垂直通常可以有两个途径,一是利用两个平面垂直的判定定理将面面垂直问题转化为线面垂直进而转化为线线垂直;二是直接求解两个平面的法向量,证明两个法向量垂直,从而得到两个平面垂直.即时训练5-1:如图所示,在直三棱柱ABC-A1B1C1中,AB⊥BC,AB=BC=2,BB1= 1,E为BB1的中点,证明:平面AEC1⊥平面AA1C1C.
