高中数学新人教A版选修2-1课件:第三章空间向量与立体几何章末总结(48张)
文档属性
| 名称 | 高中数学新人教A版选修2-1课件:第三章空间向量与立体几何章末总结(48张) |  | |
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-20 19:44:35 | ||
图片预览









文档简介
课件48张PPT。章末总结点击进入 网络建构主题串讲一、空间向量与线面位置关系
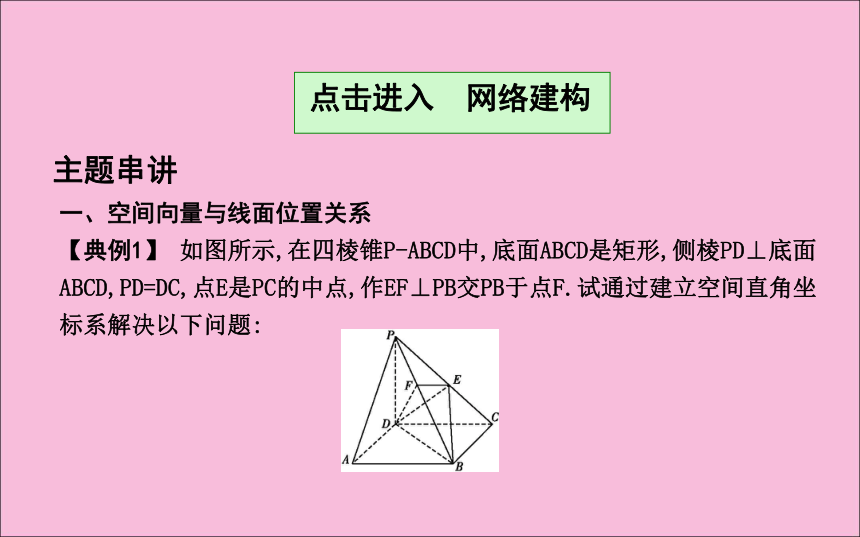
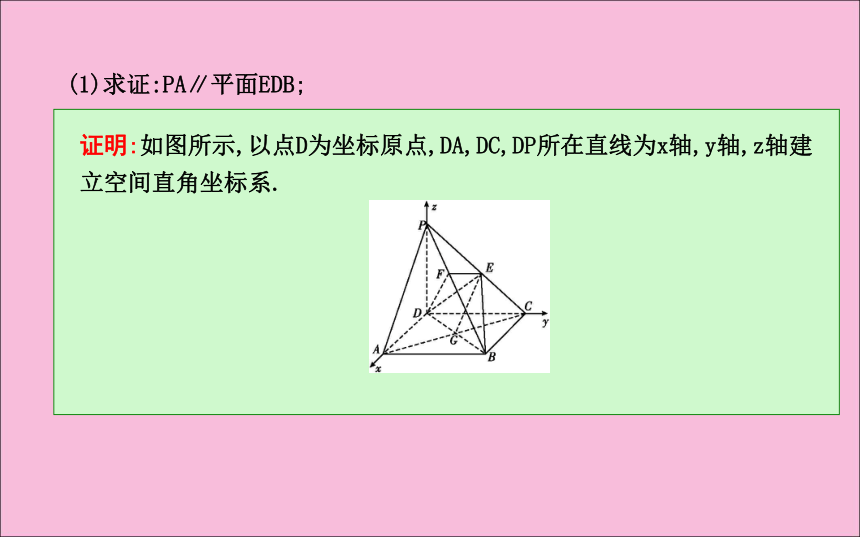
【典例1】 如图所示,在四棱锥P-ABCD中,底面ABCD是矩形,侧棱PD⊥底面ABCD,PD=DC,点E是PC的中点,作EF⊥PB交PB于点F.试通过建立空间直角坐标系解决以下问题:(1)求证:PA∥平面EDB;证明:如图所示,以点D为坐标原点,DA,DC,DP所在直线为x轴,y轴,z轴建立空间直角坐标系.(2)求证:PB⊥平面EFD.即时训练1-1:在四棱锥P-ABCD中,AB⊥AD,CD⊥AD,PA⊥底面ABCD,PA=AD= CD=2AB=2,M为PC的中点.
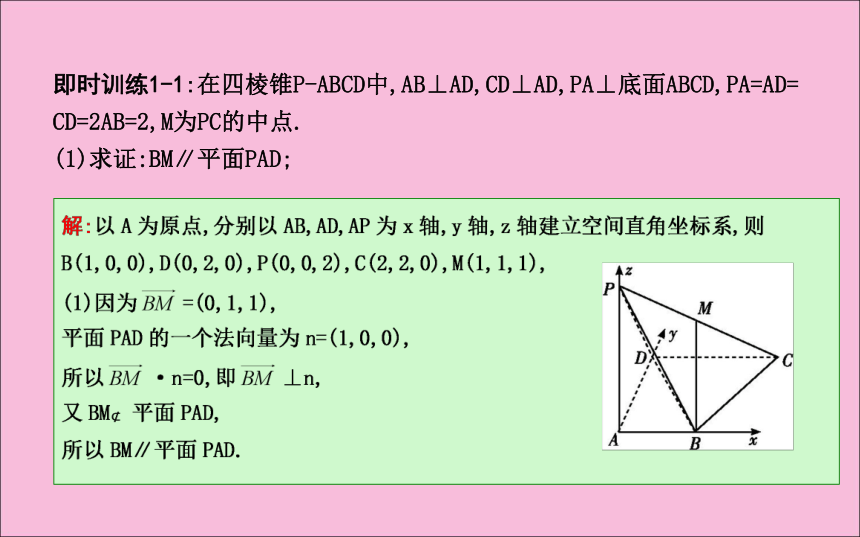
(1)求证:BM∥平面PAD;(2)平面PAD内是否存在一点N,使MN⊥平面PBD?若存在,确定N的位置,若不存在,说明理由.二、空间向量与空间角(1)求PB的长度;(2)求证:PB⊥平面ABCE;(3)求直线AB与平面APE所成角的正弦值.即时训练2-1:如图,在直三棱柱ABC-A1B1C1中,底面ABC为边长为2的正三角形,D是棱A1C1的中点,CC1=h(h>0).
(1)证明:BC1∥平面AB1D;(1)证明:法一 连接A1B交AB1于E,连接DE,
则DE是△A1BC1的中位线.
所以DE∥BC1.
又DE?平面AB1D,
BC1?平面AB1D,
故BC1∥平面AB1D.法二 取AC的中点F,连接BF,C1F.
因为AF∥DC1,且AF=DC1,
所以四边形AFC1D是平行四边形,
故AD∥FC1.
又FC1?平面BFC1,
AD?平面BFC1,
故AD∥平面BFC1.同理:DB1∥平面BFC1.
所以平面ADB1∥平面BFC1.
故BC1∥平面AB1D.三、用空间向量求距离
【典例3】 如图所示,已知四边形ABCD,EADM和MDCF都是边长为a的正方形,点P,Q分别是ED,AC的中点,求:(2)P点到平面EFB的距离.即时训练3-1:在直三棱柱ABC-A1B1C1中,AB=AC=AA1=2,∠BAC=90°,M为BB1的中点,N为BC的中点.
(1)求点M到直线AC1的距离;(2)求点N到平面MA1C1的距离.四、易错易误辨析
1.混淆向量与实数的运算性质致误
【典例4】 已知a,b都是非零向量,且向量a+3b与7a-5b垂直,向量a-4b与7a-2b垂直,求向量a,b的夹角.错因分析:向量的运算性质与实数不同,若b·(2a-b)=0不一定有a=0或2a-b=0,本题在此处误当作实数运算而导致了错误.2.对所求角与向量夹角的关系不理解致误
【典例5】 正方体ABCD-A1B1C1D1中,求二面角A-BD1-C的大小.错解:以D为坐标原点建立如图所示的空间直角坐标系,设正方体的棱长为1,
则D(0,0,0),A1(1,0,1),C1(0,1,1).错因分析:用法向量的夹角判断二面角的大小时出现错误,根据法向量的方向可知,二面角为钝角,而不是锐角.正解:以D为坐标原点建立如图所示的空间直角坐标系,
设正方体的棱长为1,
则D(0,0,0),A1(1,0,1),C1(0,1,1).真题体验1.(2017·全国Ⅰ卷)如图,在四棱锥P-ABCD中,AB∥CD,且∠BAP=∠CDP =90°.
(1)证明:平面PAB⊥平面PAD;(1)证明:由已知∠BAP=∠CDP=90°,
得AB⊥AP,CD⊥PD.
由于AB∥CD,故AB⊥PD,
从而AB⊥平面PAD.
又AB?平面PAB,所以平面PAB⊥平面PAD.(2)若PA=PD=AB=DC,∠APD=90°,求二面角A-PB-C的余弦值.(1)证明:直线CE∥平面PAB;(2)点M在棱PC上,且直线BM与底面ABCD所成角为45°,求二面角M-AB-D的余弦值.3.(2017·全国Ⅲ卷)如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.
(1)证明:平面ACD⊥平面ABC;解:(1)由题设可得△ABD≌△CBD,从而AD=DC.
又△ACD是直角三角形,所以∠ADC=90°.
取AC的中点O,连接DO,BO,则DO⊥AC,DO=AO.
又由于△ABC是正三角形,故BO⊥AC.
所以∠DOB为二面角D-AC-B的平面角.
在Rt△AOB中,BO2+AO2=AB2.
又AB=BD,所以BO2+DO2=BO2+AO2=AB2=BD2,故∠DOB=90°.
所以平面ACD⊥平面ABC.(2)过AC的平面交BD于点E,若平面AEC把四面体ABCD分成体积相等的两部分,求二面角D-AE-C的余弦值.(1)求证:M为PB的中点;(1)证明:设AC,BD交点为E,连接ME.
因为PD∥平面MAC,
平面MAC∩平面PDB=ME,
所以PD∥ME.
因为ABCD是正方形,
所以E为BD的中点.
所以M为PB的中点.(2)求二面角B-PD-A的大小;(2)解:取AD的中点O,连接OP,OE.
因为PA=PD,
所以OP⊥AD.
又因为平面PAD⊥平面ABCD,
且OP?平面PAD,平面PAD∩平面ABCD=AD,
所以OP⊥平面ABCD.(3)求直线MC与平面BDP所成角的正弦值.5.(2017·天津卷)如图,在三棱锥P-ABC中,PA⊥底面ABC,∠BAC=90°.点D,E,N分别为棱PA,PC,BC的中点,M是线段AD的中点,PA=AC=4,AB=2.(1)求证:MN∥平面BDE;(2)求二面角C-EM-N的正弦值;解:(1)因为AP⊥BE,AB⊥BE,AB,AP?平面ABP,AB∩AP=A,
所以BE⊥平面ABP.
又BP?平面ABP,所以BE⊥BP.
又∠EBC=120°,所以∠CBP=30°.(2)当AB=3,AD=2时,求二面角E-AG-C的大小.
【典例1】 如图所示,在四棱锥P-ABCD中,底面ABCD是矩形,侧棱PD⊥底面ABCD,PD=DC,点E是PC的中点,作EF⊥PB交PB于点F.试通过建立空间直角坐标系解决以下问题:(1)求证:PA∥平面EDB;证明:如图所示,以点D为坐标原点,DA,DC,DP所在直线为x轴,y轴,z轴建立空间直角坐标系.(2)求证:PB⊥平面EFD.即时训练1-1:在四棱锥P-ABCD中,AB⊥AD,CD⊥AD,PA⊥底面ABCD,PA=AD= CD=2AB=2,M为PC的中点.
(1)求证:BM∥平面PAD;(2)平面PAD内是否存在一点N,使MN⊥平面PBD?若存在,确定N的位置,若不存在,说明理由.二、空间向量与空间角(1)求PB的长度;(2)求证:PB⊥平面ABCE;(3)求直线AB与平面APE所成角的正弦值.即时训练2-1:如图,在直三棱柱ABC-A1B1C1中,底面ABC为边长为2的正三角形,D是棱A1C1的中点,CC1=h(h>0).
(1)证明:BC1∥平面AB1D;(1)证明:法一 连接A1B交AB1于E,连接DE,
则DE是△A1BC1的中位线.
所以DE∥BC1.
又DE?平面AB1D,
BC1?平面AB1D,
故BC1∥平面AB1D.法二 取AC的中点F,连接BF,C1F.
因为AF∥DC1,且AF=DC1,
所以四边形AFC1D是平行四边形,
故AD∥FC1.
又FC1?平面BFC1,
AD?平面BFC1,
故AD∥平面BFC1.同理:DB1∥平面BFC1.
所以平面ADB1∥平面BFC1.
故BC1∥平面AB1D.三、用空间向量求距离
【典例3】 如图所示,已知四边形ABCD,EADM和MDCF都是边长为a的正方形,点P,Q分别是ED,AC的中点,求:(2)P点到平面EFB的距离.即时训练3-1:在直三棱柱ABC-A1B1C1中,AB=AC=AA1=2,∠BAC=90°,M为BB1的中点,N为BC的中点.
(1)求点M到直线AC1的距离;(2)求点N到平面MA1C1的距离.四、易错易误辨析
1.混淆向量与实数的运算性质致误
【典例4】 已知a,b都是非零向量,且向量a+3b与7a-5b垂直,向量a-4b与7a-2b垂直,求向量a,b的夹角.错因分析:向量的运算性质与实数不同,若b·(2a-b)=0不一定有a=0或2a-b=0,本题在此处误当作实数运算而导致了错误.2.对所求角与向量夹角的关系不理解致误
【典例5】 正方体ABCD-A1B1C1D1中,求二面角A-BD1-C的大小.错解:以D为坐标原点建立如图所示的空间直角坐标系,设正方体的棱长为1,
则D(0,0,0),A1(1,0,1),C1(0,1,1).错因分析:用法向量的夹角判断二面角的大小时出现错误,根据法向量的方向可知,二面角为钝角,而不是锐角.正解:以D为坐标原点建立如图所示的空间直角坐标系,
设正方体的棱长为1,
则D(0,0,0),A1(1,0,1),C1(0,1,1).真题体验1.(2017·全国Ⅰ卷)如图,在四棱锥P-ABCD中,AB∥CD,且∠BAP=∠CDP =90°.
(1)证明:平面PAB⊥平面PAD;(1)证明:由已知∠BAP=∠CDP=90°,
得AB⊥AP,CD⊥PD.
由于AB∥CD,故AB⊥PD,
从而AB⊥平面PAD.
又AB?平面PAB,所以平面PAB⊥平面PAD.(2)若PA=PD=AB=DC,∠APD=90°,求二面角A-PB-C的余弦值.(1)证明:直线CE∥平面PAB;(2)点M在棱PC上,且直线BM与底面ABCD所成角为45°,求二面角M-AB-D的余弦值.3.(2017·全国Ⅲ卷)如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.
(1)证明:平面ACD⊥平面ABC;解:(1)由题设可得△ABD≌△CBD,从而AD=DC.
又△ACD是直角三角形,所以∠ADC=90°.
取AC的中点O,连接DO,BO,则DO⊥AC,DO=AO.
又由于△ABC是正三角形,故BO⊥AC.
所以∠DOB为二面角D-AC-B的平面角.
在Rt△AOB中,BO2+AO2=AB2.
又AB=BD,所以BO2+DO2=BO2+AO2=AB2=BD2,故∠DOB=90°.
所以平面ACD⊥平面ABC.(2)过AC的平面交BD于点E,若平面AEC把四面体ABCD分成体积相等的两部分,求二面角D-AE-C的余弦值.(1)求证:M为PB的中点;(1)证明:设AC,BD交点为E,连接ME.
因为PD∥平面MAC,
平面MAC∩平面PDB=ME,
所以PD∥ME.
因为ABCD是正方形,
所以E为BD的中点.
所以M为PB的中点.(2)求二面角B-PD-A的大小;(2)解:取AD的中点O,连接OP,OE.
因为PA=PD,
所以OP⊥AD.
又因为平面PAD⊥平面ABCD,
且OP?平面PAD,平面PAD∩平面ABCD=AD,
所以OP⊥平面ABCD.(3)求直线MC与平面BDP所成角的正弦值.5.(2017·天津卷)如图,在三棱锥P-ABC中,PA⊥底面ABC,∠BAC=90°.点D,E,N分别为棱PA,PC,BC的中点,M是线段AD的中点,PA=AC=4,AB=2.(1)求证:MN∥平面BDE;(2)求二面角C-EM-N的正弦值;解:(1)因为AP⊥BE,AB⊥BE,AB,AP?平面ABP,AB∩AP=A,
所以BE⊥平面ABP.
又BP?平面ABP,所以BE⊥BP.
又∠EBC=120°,所以∠CBP=30°.(2)当AB=3,AD=2时,求二面角E-AG-C的大小.
