高中数学新人教A版选修2-1课件:第一章常用逻辑用语1.1.2四种命题1.1.3四种命题间的相互关系(27张)
文档属性
| 名称 | 高中数学新人教A版选修2-1课件:第一章常用逻辑用语1.1.2四种命题1.1.3四种命题间的相互关系(27张) |

|
|
| 格式 | zip | ||
| 文件大小 | 209.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-20 00:00:00 | ||
图片预览








文档简介
课件27张PPT。1.1.2 四种命题
1.1.3 四种命题间的相互关系课标要求:1.了解“若p,则q”形式的命题及其逆命题、否命题与逆否命题.2.能够把一个“若p,则q”形式的命题熟练地写出其逆命题、否命题和逆否命题.3.掌握四种命题之间的关系及真假性之间的联系,会利用命题的等价性解决问题. 自主学习1.互逆命题
对于两个命题,如果一个命题的条件和结论分别是另一个命题的 ,那么我们把这样的两个命题叫做互逆命题.其中一个命题叫做原命题,另一个叫做原命题的逆命题.
2.互否命题
对于两个命题,其中一个命题的条件和结论恰好是另一个命题的 .和 ,我们把这样的两个命题叫做互否命题.如果把其中的一个命题叫做原命题,那么另一个叫做原命题的否命题.知识探究结论和条件条件的否定结论的否定3.互为逆否命题
对于两个命题,其中一个命题的条件和结论恰好是另一个命题的 .
和 ,我们把这样的两个命题叫做互为逆否命题.如果把其中的一个命题叫做原命题,那么另一个叫做原命题的逆否命题.
用p和q分别表示原命题的条件和结论,用﹁p(读作“非p”)和﹁q(读作“非q”)分别表示p和q的否定,于是四种命题的形式就是:结论的否定条件的否定注意:(1)“逆命题、否命题、逆否命题”都是相对于原命题而言的,都是相对概念,如命题“若x≠2,则x2≠4”相对于命题“若x=2,则x2=4”是否命题,而相对于命题“若x2=4,则x=2”则是逆否命题;
(2)互逆命题、互否命题、互为逆否命题都是说两个命题之间的关系,把其中一个命题叫做原命题时,另一个命题就叫做原命题的逆命题、否命题或逆否命题,即要充分理解“互为”的相对性;
(3)不是“若p,则q”形式的命题,最好先改写成“若p,则q”的形式,然后讨论其他三种命题,这样容易分清条件和结论.4.四种命题间的相互关系
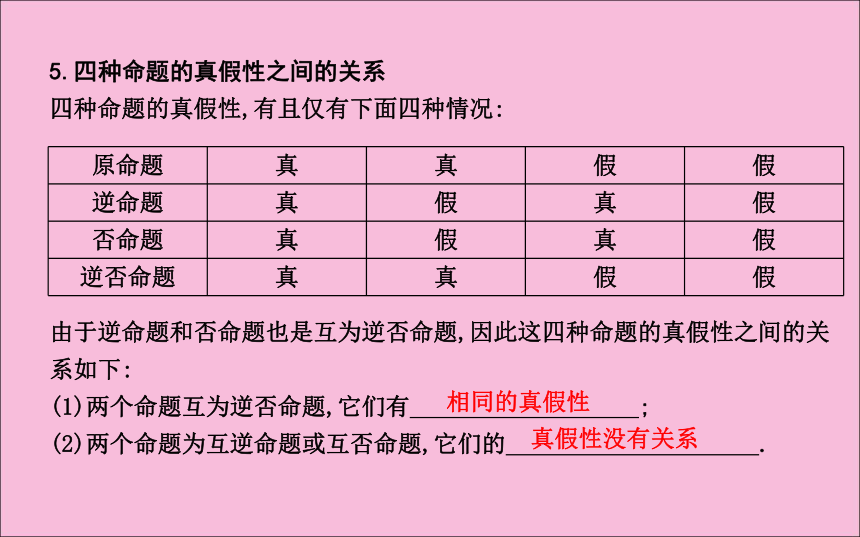
原命题、逆命题、否命题与逆否命题这四种命题之间的相互关系如图所示.5.四种命题的真假性之间的关系
四种命题的真假性,有且仅有下面四种情况:
由于逆命题和否命题也是互为逆否命题,因此这四种命题的真假性之间的关系如下:
(1)两个命题互为逆否命题,它们有 ;
(2)两个命题为互逆命题或互否命题,它们的 .相同的真假性真假性没有关系注意:四种命题中真命题个数的探究
因为原命题与逆否命题有相同的真假性,逆命题与否命题有相同真假性,所以四种命题中真命题的个数一定为偶数,即真命题的个数只可能为0,2,4.
说明:根据四种命题中真命题的个数只可能为0,2,4,可以检验写出的逆命题、否命题、逆否命题是否正确.自我检测B1.命题“若一个数是负数,则它的平方是正数”的逆命题是( )
(A)若一个数是负数,则它的平方不是正数
(B)若一个数的平方是正数,则它是负数
(C)若一个数不是负数,则它的平方不是正数
(D)若一个数的平方不是正数,则它不是负数C3.命题“a,b都是奇数,则a+b是偶数”的逆否命题是( )
(A)若a,b都不是奇数,则a+b是偶数
(B)若a+b是奇数,则a,b都是偶数
(C)若a+b不是偶数,则a,b都不是奇数
(D)若a+b不是偶数,则a,b不都是奇数
4.命题“若x>1,则x>0”的逆命题是 ,逆否命题是
. 答案:若x>0,则x>1 若x≤0,则x≤1D5.在原命题“若A∪B≠B,则A∩B≠A”与它的逆命题、否命题、逆否命题中,真命题的个数为 .?解析:逆命题为“若A∩B≠A,则A∪B≠B”;
否命题为“若A∪B=B,则A∩B=A”;
逆否命题为“若A∩B=A,则A∪B=B”;
全为真命题.
答案:4题型一四种命题的概念 课堂探究【例1】 把下列命题改写成“若p,则q”的形式,并写出它们的逆命题、否命题与逆否命题.
(1)全等三角形的对应边相等;解:(1)原命题:若两个三角形全等,则这两个三角形三边对应相等;
逆命题:若两个三角形三边对应相等,则这两个三角形全等;
否命题:若两个三角形不全等,则这两个三角形三边对应不相等;
逆否命题:若两个三角形三边对应不相等,则这两个三角形不全等.(2)当x=2时,x2-3x+2=0;
(3)正数a的平方根不等于0.解:(2)原命题:若x=2,则x2-3x+2=0;
逆命题:若x2-3x+2=0,则x=2;
否命题:若x≠2,则x2-3x+2≠0;
逆否命题:若x2-3x+2≠0,则x≠2.
(3)原命题:若a是正数,则a的平方根不等于0.
逆命题:若a的平方根不等于0,则a是正数.
否命题:若a不是正数,则a的平方根等于0.
逆否命题:若a的平方根等于0,则a不是正数.方法技巧 (1)由原命题写出其他三种命题,关键要分清原命题的条件和结论,将条件与结论互换即得逆命题,将条件和结论同时否定即得否命题,将条件和结论互换的同时,进行否定即得逆否命题.
(2)如果原命题含有大前提,在写出原命题的逆命题、否命题、逆否命题时,必须注意各命题中的大前提不变.解:(1)改写成“若一个数是无理数,则它的平方是有理数”.
逆命题:若一个数的平方是有理数,则它是无理数.
否命题:若一个数不是无理数,则它的平方不是有理数.
逆否命题:若一个数的平方不是有理数,则它不是无理数.
(2)逆命题:若x=2或x=-3,则x2+x-6=0.
否命题:若x2+x-6≠0,则x≠2且x≠-3.
逆否命题:若x≠2且x≠-3,则x2+x-6≠0.即时训练1-1:写出下列命题的逆命题、否命题和逆否命题.
(1)无理数的平方是有理数;
(2)当x2+x-6=0时,x=2或x=-3;(3)垂直于同一平面的两直线平行;
(4)若m·n<0,则方程mx2-x+n=0有实数根.解:(3)逆命题:如果两条直线平行,那么这两条直线垂直于同一个平面.
否命题:如果两条直线不垂直于同一平面,那么这两条直线不平行.
逆否命题:如果两条直线不平行,那么这两条直线不垂直于同一平面.
(4)逆命题:若方程mx2-x+n=0有实数根,则m·n<0.
否命题:若m·n≥0,则方程mx2-x+n=0没有实数根.
逆否命题:若方程mx2-x+n=0没有实数根,则m·n≥0.题型二四种命题的关系及其真假判断【例2】 判断下列命题的真假.
(1)“若x2+y2≠0,则x,y不全为零”的否命题;
(2)“正三角形都相似”的逆命题;
(3)“若m>0,则x2+x-m=0有实根”的逆否命题;解:(1)原命题的否命题为“若x2+y2=0,则x,y全为零”.真命题.
(2)原命题的逆命题为“若三角形相似,则这些三角形是正三角形”.假命题.(4)“若m>0,则x2+x-m=0有实根”的逆命题;
(5)“若m>0,则mx2+x-1=0有实根”的逆否命题. 解决此类题目的关键是牢记四种命题的概念,原命题与它的逆否命题同真同假,原命题的否命题与逆命题也互为逆否命题,同真同假,故只判断两者中的一个即可.方法技巧即时训练2-1:(1)设m,n是向量,命题“若m=n,则|m|=|n|”与它的逆命题、否命题、逆否命题这4个命题中,真命题的个数是( )
(A)0 (B)1 (C)2 (D)4解析:(1)法一 原命题为真命题.
逆命题:“若|m|=|n|,则m=n”为假命题,
否命题:“若m≠n,则|m|≠|n|”为假命题.
逆否命题:“若|m|≠|n|,则m≠n”为真命题.
故四个命题中,真命题的个数是2.故选C.
法二 原命题为真命题,则其逆否命题也为真命题.
逆命题:“若|m|=|n|,则m=n”为假命题,则否命题也为假命题.故四个命题中,真命题的个数是2.故选C.等价命题的应用题型三【例3】 (12分)已知函数f(x)在(-∞,+∞)上是增函数,a,b∈R,对命题“若a+b≥0,则f(a)+f(b)≥f(-a)+f(-b).”
写出其逆命题,判断其真假,并证明你的结论.规范解答:逆命题:若f(a)+f(b)≥f(-a)+f(-b),则a+b≥0.为真命题.2分
由于逆命题与否命题具有相同的真假性,因此可转化为证明其否命题为真,即证明“若a+b<0,则f(a)+f(b)因为a+b<0,则a<-b,b<-a.
因为f(x)在(-∞,+∞)上为增函数,
则f(a)所以f(a)+f(b)因此否命题为真命题,即逆命题为真命题.………………………………12分变式探究:写出本例中命题的逆否命题,判断其真假,并证明你的结论.解:逆否命题:若f(a)+f(b)因为一个命题的真假性与它的逆否命题的真假性相同,
所以可证明原命题为真命题.
因为a+b≥0,所以a≥-b,b≥-a.
又因为f(x)在(-∞,+∞)上是增函数,
所以f(a)≥f(-b),f(b)≥f(-a).
所以f(a)+f(b)≥f(-a)+f(-b).
所以逆否命题为真命题.方法技巧 直接证明困难时,命题是否定的形式或不等式的形式时,常常考虑用证明逆否命题的方法来证明.即时训练3-1:判断命题“已知a,x为实数,若关于x的不等式x2+(2a+1)x+a2+2
≤0的解集是空集,则a<2”的逆否命题的真假.解:法一 原命题的逆否命题为“已知a,x为实数,若a≥2,则关于x的不等式x2+(2a+1)x+a2+2≤0的解集不是空集”.
判断真假如下:
抛物线y=x2+(2a+1)x+a2+2的开口向上,判别式Δ=(2a+1)2-4(a2+2)=4a-7,
因为a≥2,所以4a-7>0,
即抛物线与x轴有交点,所以关于x的不等式x2+(2a+1)x+a2+2≤0的解集不是空集,故原命题的逆否命题为真.
1.1.3 四种命题间的相互关系课标要求:1.了解“若p,则q”形式的命题及其逆命题、否命题与逆否命题.2.能够把一个“若p,则q”形式的命题熟练地写出其逆命题、否命题和逆否命题.3.掌握四种命题之间的关系及真假性之间的联系,会利用命题的等价性解决问题. 自主学习1.互逆命题
对于两个命题,如果一个命题的条件和结论分别是另一个命题的 ,那么我们把这样的两个命题叫做互逆命题.其中一个命题叫做原命题,另一个叫做原命题的逆命题.
2.互否命题
对于两个命题,其中一个命题的条件和结论恰好是另一个命题的 .和 ,我们把这样的两个命题叫做互否命题.如果把其中的一个命题叫做原命题,那么另一个叫做原命题的否命题.知识探究结论和条件条件的否定结论的否定3.互为逆否命题
对于两个命题,其中一个命题的条件和结论恰好是另一个命题的 .
和 ,我们把这样的两个命题叫做互为逆否命题.如果把其中的一个命题叫做原命题,那么另一个叫做原命题的逆否命题.
用p和q分别表示原命题的条件和结论,用﹁p(读作“非p”)和﹁q(读作“非q”)分别表示p和q的否定,于是四种命题的形式就是:结论的否定条件的否定注意:(1)“逆命题、否命题、逆否命题”都是相对于原命题而言的,都是相对概念,如命题“若x≠2,则x2≠4”相对于命题“若x=2,则x2=4”是否命题,而相对于命题“若x2=4,则x=2”则是逆否命题;
(2)互逆命题、互否命题、互为逆否命题都是说两个命题之间的关系,把其中一个命题叫做原命题时,另一个命题就叫做原命题的逆命题、否命题或逆否命题,即要充分理解“互为”的相对性;
(3)不是“若p,则q”形式的命题,最好先改写成“若p,则q”的形式,然后讨论其他三种命题,这样容易分清条件和结论.4.四种命题间的相互关系
原命题、逆命题、否命题与逆否命题这四种命题之间的相互关系如图所示.5.四种命题的真假性之间的关系
四种命题的真假性,有且仅有下面四种情况:
由于逆命题和否命题也是互为逆否命题,因此这四种命题的真假性之间的关系如下:
(1)两个命题互为逆否命题,它们有 ;
(2)两个命题为互逆命题或互否命题,它们的 .相同的真假性真假性没有关系注意:四种命题中真命题个数的探究
因为原命题与逆否命题有相同的真假性,逆命题与否命题有相同真假性,所以四种命题中真命题的个数一定为偶数,即真命题的个数只可能为0,2,4.
说明:根据四种命题中真命题的个数只可能为0,2,4,可以检验写出的逆命题、否命题、逆否命题是否正确.自我检测B1.命题“若一个数是负数,则它的平方是正数”的逆命题是( )
(A)若一个数是负数,则它的平方不是正数
(B)若一个数的平方是正数,则它是负数
(C)若一个数不是负数,则它的平方不是正数
(D)若一个数的平方不是正数,则它不是负数C3.命题“a,b都是奇数,则a+b是偶数”的逆否命题是( )
(A)若a,b都不是奇数,则a+b是偶数
(B)若a+b是奇数,则a,b都是偶数
(C)若a+b不是偶数,则a,b都不是奇数
(D)若a+b不是偶数,则a,b不都是奇数
4.命题“若x>1,则x>0”的逆命题是 ,逆否命题是
. 答案:若x>0,则x>1 若x≤0,则x≤1D5.在原命题“若A∪B≠B,则A∩B≠A”与它的逆命题、否命题、逆否命题中,真命题的个数为 .?解析:逆命题为“若A∩B≠A,则A∪B≠B”;
否命题为“若A∪B=B,则A∩B=A”;
逆否命题为“若A∩B=A,则A∪B=B”;
全为真命题.
答案:4题型一四种命题的概念 课堂探究【例1】 把下列命题改写成“若p,则q”的形式,并写出它们的逆命题、否命题与逆否命题.
(1)全等三角形的对应边相等;解:(1)原命题:若两个三角形全等,则这两个三角形三边对应相等;
逆命题:若两个三角形三边对应相等,则这两个三角形全等;
否命题:若两个三角形不全等,则这两个三角形三边对应不相等;
逆否命题:若两个三角形三边对应不相等,则这两个三角形不全等.(2)当x=2时,x2-3x+2=0;
(3)正数a的平方根不等于0.解:(2)原命题:若x=2,则x2-3x+2=0;
逆命题:若x2-3x+2=0,则x=2;
否命题:若x≠2,则x2-3x+2≠0;
逆否命题:若x2-3x+2≠0,则x≠2.
(3)原命题:若a是正数,则a的平方根不等于0.
逆命题:若a的平方根不等于0,则a是正数.
否命题:若a不是正数,则a的平方根等于0.
逆否命题:若a的平方根等于0,则a不是正数.方法技巧 (1)由原命题写出其他三种命题,关键要分清原命题的条件和结论,将条件与结论互换即得逆命题,将条件和结论同时否定即得否命题,将条件和结论互换的同时,进行否定即得逆否命题.
(2)如果原命题含有大前提,在写出原命题的逆命题、否命题、逆否命题时,必须注意各命题中的大前提不变.解:(1)改写成“若一个数是无理数,则它的平方是有理数”.
逆命题:若一个数的平方是有理数,则它是无理数.
否命题:若一个数不是无理数,则它的平方不是有理数.
逆否命题:若一个数的平方不是有理数,则它不是无理数.
(2)逆命题:若x=2或x=-3,则x2+x-6=0.
否命题:若x2+x-6≠0,则x≠2且x≠-3.
逆否命题:若x≠2且x≠-3,则x2+x-6≠0.即时训练1-1:写出下列命题的逆命题、否命题和逆否命题.
(1)无理数的平方是有理数;
(2)当x2+x-6=0时,x=2或x=-3;(3)垂直于同一平面的两直线平行;
(4)若m·n<0,则方程mx2-x+n=0有实数根.解:(3)逆命题:如果两条直线平行,那么这两条直线垂直于同一个平面.
否命题:如果两条直线不垂直于同一平面,那么这两条直线不平行.
逆否命题:如果两条直线不平行,那么这两条直线不垂直于同一平面.
(4)逆命题:若方程mx2-x+n=0有实数根,则m·n<0.
否命题:若m·n≥0,则方程mx2-x+n=0没有实数根.
逆否命题:若方程mx2-x+n=0没有实数根,则m·n≥0.题型二四种命题的关系及其真假判断【例2】 判断下列命题的真假.
(1)“若x2+y2≠0,则x,y不全为零”的否命题;
(2)“正三角形都相似”的逆命题;
(3)“若m>0,则x2+x-m=0有实根”的逆否命题;解:(1)原命题的否命题为“若x2+y2=0,则x,y全为零”.真命题.
(2)原命题的逆命题为“若三角形相似,则这些三角形是正三角形”.假命题.(4)“若m>0,则x2+x-m=0有实根”的逆命题;
(5)“若m>0,则mx2+x-1=0有实根”的逆否命题. 解决此类题目的关键是牢记四种命题的概念,原命题与它的逆否命题同真同假,原命题的否命题与逆命题也互为逆否命题,同真同假,故只判断两者中的一个即可.方法技巧即时训练2-1:(1)设m,n是向量,命题“若m=n,则|m|=|n|”与它的逆命题、否命题、逆否命题这4个命题中,真命题的个数是( )
(A)0 (B)1 (C)2 (D)4解析:(1)法一 原命题为真命题.
逆命题:“若|m|=|n|,则m=n”为假命题,
否命题:“若m≠n,则|m|≠|n|”为假命题.
逆否命题:“若|m|≠|n|,则m≠n”为真命题.
故四个命题中,真命题的个数是2.故选C.
法二 原命题为真命题,则其逆否命题也为真命题.
逆命题:“若|m|=|n|,则m=n”为假命题,则否命题也为假命题.故四个命题中,真命题的个数是2.故选C.等价命题的应用题型三【例3】 (12分)已知函数f(x)在(-∞,+∞)上是增函数,a,b∈R,对命题“若a+b≥0,则f(a)+f(b)≥f(-a)+f(-b).”
写出其逆命题,判断其真假,并证明你的结论.规范解答:逆命题:若f(a)+f(b)≥f(-a)+f(-b),则a+b≥0.为真命题.2分
由于逆命题与否命题具有相同的真假性,因此可转化为证明其否命题为真,即证明“若a+b<0,则f(a)+f(b)
因为f(x)在(-∞,+∞)上为增函数,
则f(a)
所以可证明原命题为真命题.
因为a+b≥0,所以a≥-b,b≥-a.
又因为f(x)在(-∞,+∞)上是增函数,
所以f(a)≥f(-b),f(b)≥f(-a).
所以f(a)+f(b)≥f(-a)+f(-b).
所以逆否命题为真命题.方法技巧 直接证明困难时,命题是否定的形式或不等式的形式时,常常考虑用证明逆否命题的方法来证明.即时训练3-1:判断命题“已知a,x为实数,若关于x的不等式x2+(2a+1)x+a2+2
≤0的解集是空集,则a<2”的逆否命题的真假.解:法一 原命题的逆否命题为“已知a,x为实数,若a≥2,则关于x的不等式x2+(2a+1)x+a2+2≤0的解集不是空集”.
判断真假如下:
抛物线y=x2+(2a+1)x+a2+2的开口向上,判别式Δ=(2a+1)2-4(a2+2)=4a-7,
因为a≥2,所以4a-7>0,
即抛物线与x轴有交点,所以关于x的不等式x2+(2a+1)x+a2+2≤0的解集不是空集,故原命题的逆否命题为真.
