高中数学新人教A版选修2-1课件:第二章圆锥曲线与方程2.2.2椭圆的简单几何性质(31张)
文档属性
| 名称 | 高中数学新人教A版选修2-1课件:第二章圆锥曲线与方程2.2.2椭圆的简单几何性质(31张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-20 00:00:00 | ||
图片预览











文档简介
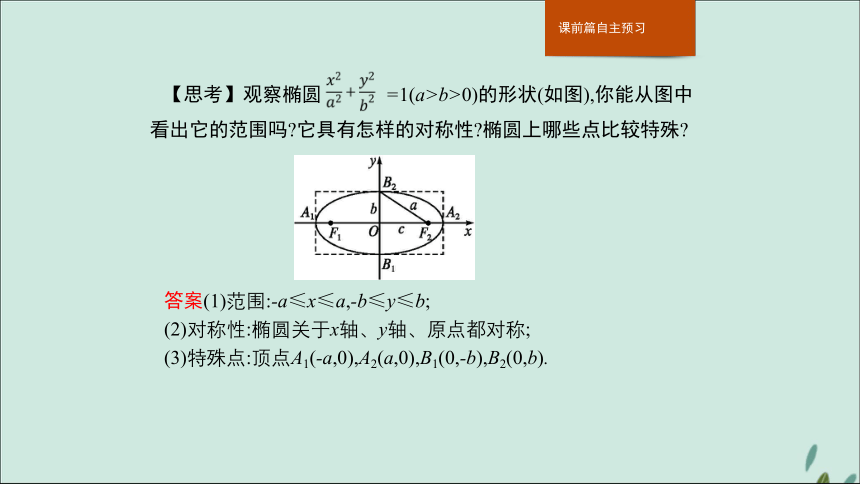
课件31张PPT。2.2.2 椭圆的简单几何性质【思考】观察椭圆 =1(a>b>0)的形状(如图),你能从图中看出它的范围吗?它具有怎样的对称性?椭圆上哪些点比较特殊?
答案(1)范围:-a≤x≤a,-b≤y≤b;
(2)对称性:椭圆关于x轴、y轴、原点都对称;
(3)特殊点:顶点A1(-a,0),A2(a,0),B1(0,-b),B2(0,b).1.椭圆的几何性质 名师点拨1.椭圆的范围给出了椭圆上的点的横坐标、纵坐标的取值范围,在求解一些存在性、判断性问题中有着重要的应用,也可用于求最值、求轨迹等问题时的检验等.
2.利用方程研究曲线对称性的方法如下:
(1)若把曲线方程中的x换成-x,方程不变,则曲线关于y轴对称;
(2)若把曲线方程中的y换成-y,方程不变,则曲线关于x轴对称;
(3)若同时把曲线方程中的x换成-x,y换成-y,方程不变,则曲线关于原点对称.【做一做1】 椭圆x2+4y2=1的离心率等于( ) 答案A 【做一做2】 若点P(m,n)是椭圆 =1上任意一点,则m的取值范围是 ,n的取值范围是 .?【做一做3】 已知椭圆 =1,则其顶点坐标分别为 ,焦点坐标为 ,长轴长等于 ,短轴长等于 ,焦距等于 .?【做一做4】 判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
(1)椭圆 =1(a>b)的长轴长为a,短轴长为b.( )
(2)椭圆的离心率越大,则椭圆越接近于圆.( )
(3)若一个矩形的四个顶点都在椭圆上,则这四个顶点关于椭圆的中心对称.( )
答案(1)× (2)× (3)√探究一探究二探究三当堂检测 探究一根据椭圆的标准方程研究其几何性质
例1 求椭圆9x2+16y2=144的长轴长、短轴长、离心率、焦点和顶点坐标.探究一探究二探究三当堂检测延伸探究本例中若把椭圆方程改为“9x2+16y2=1”,求其长轴长、短轴长、离心率、焦点和顶点坐标.探究一探究二探究三当堂检测反思感悟确定椭圆几何性质的基本步骤
(1)化标准,把椭圆方程化成标准形式;
(2)定位置,根据标准方程中x2,y2对应分母的大小来确定焦点位置;
(3)求参数,写出a,b的值,并求出c的值;
(4)写性质,按要求写出椭圆的简单几何性质.探究一探究二探究三当堂检测变式训练1已知椭圆C1: =1,设椭圆C2与椭圆C1的长轴长、短轴长分别相等,且椭圆C2的焦点在y轴上.
(1)求椭圆C1的长半轴长、短半轴长、焦点坐标及离心率;
(2)写出椭圆C2的方程,并研究其性质.探究一探究二探究三当堂检测探究二根据椭圆的几何性质求其标准方程
例2 根据下列条件求椭圆的标准方程:
(1)椭圆过点(3,0),离心率e= ;
(2)在x轴上的一个焦点,与短轴两个端点的连线互相垂直,且焦距为8.
思路分析(1)焦点位置不确定,应分类讨论;(2)结合图形求出a,b,c的值代入即可.探究一探究二探究三当堂检测探究一探究二探究三当堂检测(2)设椭圆的标准方程为 =1(a>b>0).
如图所示,△A1FA2为等腰直角三角形,
OF为斜边A1A2的中线(高),
且|OF|=c,|A1A2|=2b,
∴c=b=4,∴a2=b2+c2=32.
故所求椭圆的标准方程为 =1.探究一探究二探究三当堂检测反思感悟根据椭圆的性质求方程
1.已知椭圆的几何性质,求其标准方程主要采用待定系数法,解题步骤为:
(1)确定焦点所在的位置,以确定椭圆标准方程的形式;
(2)确立关于a,b,c的方程(组),求出参数a,b,c;
(3)写出标准方程.
2.在求椭圆方程时,要注意根据题目条件判断焦点所在的坐标轴,从而确定方程的形式,若不能确定焦点所在坐标轴,则应进行讨论.一般地,已知椭圆的焦点坐标时,可以确定焦点位置,而已知离心率、长轴长、短轴长、焦距时,则不能确定焦点位置.探究一探究二探究三当堂检测变式训练2已知椭圆的长轴长是短轴长的2倍,且经过点A(2,0),求椭圆的标准方程. 探究一探究二探究三当堂检测探究三椭圆的离心率问题
例3 (1)已知椭圆的焦距不小于短轴长,求椭圆的离心率的取值范围.
(2)椭圆 =1(a>b>0)的半焦距为c,若直线y=2x与椭圆一个交点的横坐标恰为c,求椭圆的离心率.思路分析(1)依题意先建立c与b的不等式,再转化为a,c的不等式,即可求得离心率的取值范围;(2)根据题意,建立参数a,b,c的方程求解,注意椭圆定义的灵活运用.探究一探究二探究三当堂检测探究一探究二探究三当堂检测反思感悟离心率的求法
(3)若已知a,b,c的关系,则可转化为a,c的方程或不等式,进而得到关于e的方程或不等式进行求解.探究一探究二探究三当堂检测变式训练3若直线l:x-2y+2=0过椭圆的左焦点F1和一个顶点B,则椭圆离心率为( )答案D 探究一探究二探究三当堂检测思维辨析
一题多变——求椭圆的离心率探究一探究二探究三当堂检测答案D 探究一探究二探究三当堂检测变式训练1(变条件)若将本例中“PF2⊥F1F2,∠PF1F2=30°”改为“∠PF2F1=75°,∠PF1F2=45°”,求椭圆C的离心率.解在△PF1F2中,
∵∠PF1F2=45°,∠PF2F1=75°,
∴∠F1PF2=60°,
设|PF1|=m,|PF2|=n,|F1F2|=2c,椭圆的长轴长为2a,探究一探究二探究三当堂检测变式训练2(变条件,变设问)若将本例中“PF2⊥F1F2,∠PF1F2=30°”改为“椭圆C上存在点P,使∠F1PF2为钝角”,求椭圆C的离心率的取值范围.探究一探究二探究三当堂检测1.椭圆6x2+y2=6的长轴的端点坐标是( ) 答案D 探究一探究二探究三当堂检测2.在平面直角坐标系xOy中,椭圆C的中心为原点,焦点F1,F2在x轴上,离心率为 ,点P为椭圆上一点,且△PF1F2的周长为18,则椭圆C的方程为( )答案B 探究一探究二探究三当堂检测答案A 探究一探究二探究三当堂检测探究一探究二探究三当堂检测5.已知椭圆x2+my2=1的离心率为 ,求m的值及椭圆的长轴长.
答案(1)范围:-a≤x≤a,-b≤y≤b;
(2)对称性:椭圆关于x轴、y轴、原点都对称;
(3)特殊点:顶点A1(-a,0),A2(a,0),B1(0,-b),B2(0,b).1.椭圆的几何性质 名师点拨1.椭圆的范围给出了椭圆上的点的横坐标、纵坐标的取值范围,在求解一些存在性、判断性问题中有着重要的应用,也可用于求最值、求轨迹等问题时的检验等.
2.利用方程研究曲线对称性的方法如下:
(1)若把曲线方程中的x换成-x,方程不变,则曲线关于y轴对称;
(2)若把曲线方程中的y换成-y,方程不变,则曲线关于x轴对称;
(3)若同时把曲线方程中的x换成-x,y换成-y,方程不变,则曲线关于原点对称.【做一做1】 椭圆x2+4y2=1的离心率等于( ) 答案A 【做一做2】 若点P(m,n)是椭圆 =1上任意一点,则m的取值范围是 ,n的取值范围是 .?【做一做3】 已知椭圆 =1,则其顶点坐标分别为 ,焦点坐标为 ,长轴长等于 ,短轴长等于 ,焦距等于 .?【做一做4】 判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
(1)椭圆 =1(a>b)的长轴长为a,短轴长为b.( )
(2)椭圆的离心率越大,则椭圆越接近于圆.( )
(3)若一个矩形的四个顶点都在椭圆上,则这四个顶点关于椭圆的中心对称.( )
答案(1)× (2)× (3)√探究一探究二探究三当堂检测 探究一根据椭圆的标准方程研究其几何性质
例1 求椭圆9x2+16y2=144的长轴长、短轴长、离心率、焦点和顶点坐标.探究一探究二探究三当堂检测延伸探究本例中若把椭圆方程改为“9x2+16y2=1”,求其长轴长、短轴长、离心率、焦点和顶点坐标.探究一探究二探究三当堂检测反思感悟确定椭圆几何性质的基本步骤
(1)化标准,把椭圆方程化成标准形式;
(2)定位置,根据标准方程中x2,y2对应分母的大小来确定焦点位置;
(3)求参数,写出a,b的值,并求出c的值;
(4)写性质,按要求写出椭圆的简单几何性质.探究一探究二探究三当堂检测变式训练1已知椭圆C1: =1,设椭圆C2与椭圆C1的长轴长、短轴长分别相等,且椭圆C2的焦点在y轴上.
(1)求椭圆C1的长半轴长、短半轴长、焦点坐标及离心率;
(2)写出椭圆C2的方程,并研究其性质.探究一探究二探究三当堂检测探究二根据椭圆的几何性质求其标准方程
例2 根据下列条件求椭圆的标准方程:
(1)椭圆过点(3,0),离心率e= ;
(2)在x轴上的一个焦点,与短轴两个端点的连线互相垂直,且焦距为8.
思路分析(1)焦点位置不确定,应分类讨论;(2)结合图形求出a,b,c的值代入即可.探究一探究二探究三当堂检测探究一探究二探究三当堂检测(2)设椭圆的标准方程为 =1(a>b>0).
如图所示,△A1FA2为等腰直角三角形,
OF为斜边A1A2的中线(高),
且|OF|=c,|A1A2|=2b,
∴c=b=4,∴a2=b2+c2=32.
故所求椭圆的标准方程为 =1.探究一探究二探究三当堂检测反思感悟根据椭圆的性质求方程
1.已知椭圆的几何性质,求其标准方程主要采用待定系数法,解题步骤为:
(1)确定焦点所在的位置,以确定椭圆标准方程的形式;
(2)确立关于a,b,c的方程(组),求出参数a,b,c;
(3)写出标准方程.
2.在求椭圆方程时,要注意根据题目条件判断焦点所在的坐标轴,从而确定方程的形式,若不能确定焦点所在坐标轴,则应进行讨论.一般地,已知椭圆的焦点坐标时,可以确定焦点位置,而已知离心率、长轴长、短轴长、焦距时,则不能确定焦点位置.探究一探究二探究三当堂检测变式训练2已知椭圆的长轴长是短轴长的2倍,且经过点A(2,0),求椭圆的标准方程. 探究一探究二探究三当堂检测探究三椭圆的离心率问题
例3 (1)已知椭圆的焦距不小于短轴长,求椭圆的离心率的取值范围.
(2)椭圆 =1(a>b>0)的半焦距为c,若直线y=2x与椭圆一个交点的横坐标恰为c,求椭圆的离心率.思路分析(1)依题意先建立c与b的不等式,再转化为a,c的不等式,即可求得离心率的取值范围;(2)根据题意,建立参数a,b,c的方程求解,注意椭圆定义的灵活运用.探究一探究二探究三当堂检测探究一探究二探究三当堂检测反思感悟离心率的求法
(3)若已知a,b,c的关系,则可转化为a,c的方程或不等式,进而得到关于e的方程或不等式进行求解.探究一探究二探究三当堂检测变式训练3若直线l:x-2y+2=0过椭圆的左焦点F1和一个顶点B,则椭圆离心率为( )答案D 探究一探究二探究三当堂检测思维辨析
一题多变——求椭圆的离心率探究一探究二探究三当堂检测答案D 探究一探究二探究三当堂检测变式训练1(变条件)若将本例中“PF2⊥F1F2,∠PF1F2=30°”改为“∠PF2F1=75°,∠PF1F2=45°”,求椭圆C的离心率.解在△PF1F2中,
∵∠PF1F2=45°,∠PF2F1=75°,
∴∠F1PF2=60°,
设|PF1|=m,|PF2|=n,|F1F2|=2c,椭圆的长轴长为2a,探究一探究二探究三当堂检测变式训练2(变条件,变设问)若将本例中“PF2⊥F1F2,∠PF1F2=30°”改为“椭圆C上存在点P,使∠F1PF2为钝角”,求椭圆C的离心率的取值范围.探究一探究二探究三当堂检测1.椭圆6x2+y2=6的长轴的端点坐标是( ) 答案D 探究一探究二探究三当堂检测2.在平面直角坐标系xOy中,椭圆C的中心为原点,焦点F1,F2在x轴上,离心率为 ,点P为椭圆上一点,且△PF1F2的周长为18,则椭圆C的方程为( )答案B 探究一探究二探究三当堂检测答案A 探究一探究二探究三当堂检测探究一探究二探究三当堂检测5.已知椭圆x2+my2=1的离心率为 ,求m的值及椭圆的长轴长.
