高中数学新人教A版选修2-1课件:第二章圆锥曲线与方程2.3.2双曲线的简单几何性质(32张)
文档属性
| 名称 | 高中数学新人教A版选修2-1课件:第二章圆锥曲线与方程2.3.2双曲线的简单几何性质(32张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-20 21:41:01 | ||
图片预览










文档简介
课件32张PPT。2.3.2 双曲线的简单几何性质【思考】观察下面的图形:(1)从图形上可以看出双曲线是向两端无限延伸的,那么是否与椭圆一样有范围限制?
(2)是不是轴对称图形?对称轴是哪条直线?是不是中心对称图形?对称中心是哪个点?答案(1)有限制,因为 ≥1,即x2≥a2,所以x≥a或x≤-a.
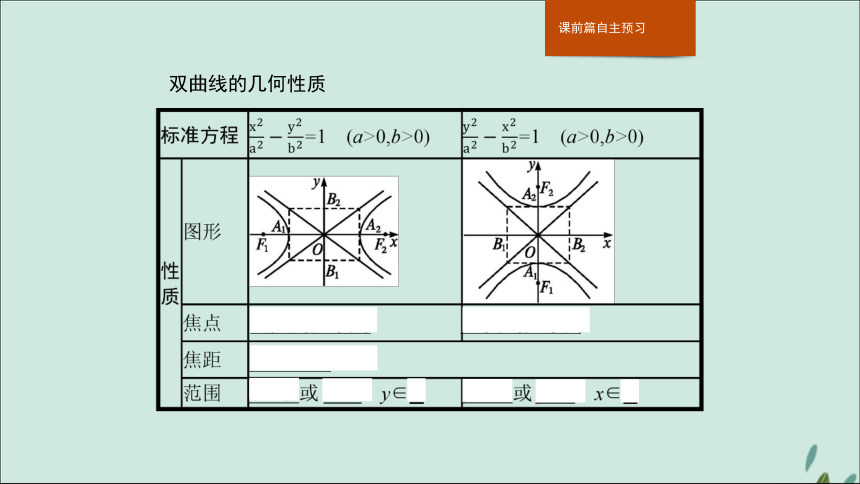
(2)关于x轴、y轴和原点都是对称的,x轴、y轴是双曲线的对称轴,原点是对称中心,又叫做双曲线的中心.双曲线的几何性质 名师点拨1.双曲线有“四点”(两个焦点、两个顶点),“四线”(两条对称轴、两条渐近线),椭圆是封闭性曲线,而双曲线是开放性曲线;双曲线有两支,故在应用时要注意点在哪一支上;根据方程判断焦点的位置时,注意双曲线与椭圆的差异性.
2.如果双曲线的方程确定,那么其渐近线的方程是唯一的,但如果双曲线的渐近线确定,那么其对应的双曲线有无数条,具有共同渐近线的双曲线方程可设为 =λ(λ≠0),当λ>0时,对应的双曲线焦点在x轴上,当λ<0时,对应的双曲线焦点在y轴上.【做一做1】 若点M(x0,y0)是双曲线 =1上支上的任意一点,则x0的取值范围是 ,y0的取值范围是 .?
解析因为a2=4,b2=25,所以a=2,b=5,所以x0∈R,y0≥2.
答案(-∞,+∞) [2,+∞)
【做一做2】 双曲线4x2-2y2=1的实轴长等于 ,虚轴长等于 ,焦距等于 .?探究一探究二探究三当堂检测 探究一双曲线的几何性质
例1 求双曲线9y2-4x2=-36的顶点坐标、焦点坐标、实轴长、虚轴长、离心率和渐近线方程.
思路分析将双曲线方程化为标准方程,先求出参数a,b,c的值,再写出各个结果.探究一探究二探究三当堂检测延伸探究若将方程9y2-4x2=-36改为9y2-4x2=36,其结果又将如何?探究一探究二探究三当堂检测反思感悟求双曲线的几何性质的基本思路
1.已知双曲线的方程研究其几何性质时,若不是标准方程,则应先化为标准方程,确定方程中a,b的对应值,利用c2=a2+b2得到c值,然后确定双曲线的焦点位置,从而写出它的几何性质.
2.求双曲线的渐近线方程时要特别注意焦点在x轴上还是在y轴上,以免写错.探究一探究二探究三当堂检测变式训练1(1)双曲线2x2-y2=-8的实轴长是 ( )答案(1)D (2)C 探究一探究二探究三当堂检测探究二根据双曲线几何性质求其标准方程
例2 求满足下列条件的双曲线的方程:
(1)已知双曲线的焦点在y轴上,实轴长与虚轴长之比为2∶3,且经过点P( ,2);
(2)已知双曲线的焦点在x轴上,离心率为 ,且经过点M(-3,2 );
(3)若双曲线的渐近线方程为2x±3y=0,且两顶点间的距离是6.
思路分析对于(1)和(2),可直接设出双曲线方程,根据条件求出参数a,b的值,即得方程;对于(3),焦点位置不确定,应分类讨论.探究一探究二探究三当堂检测探究一探究二探究三当堂检测探究一探究二探究三当堂检测反思感悟巧设双曲线方程的六种方法与技巧⑤渐近线为y=kx的双曲线方程可设为k2x2-y2=λ(λ≠0).
⑥渐近线为ax±by=0的双曲线方程可设为a2x2-b2y2=λ(λ≠0).探究一探究二探究三当堂检测变式训练2求满足下列条件的双曲线的标准方程:
(1)双曲线的实轴长与虚轴长之和等于其焦距的 倍,且一个顶点的坐标为(0,2);
(2)双曲线的渐近线方程为y=± x,且经过点A(2,-3).探究一探究二探究三当堂检测探究一探究二探究三当堂检测探究三双曲线的渐近线与离心率问题
例3 (1)过双曲线的一个焦点F2作垂直于实轴的弦PQ,F1是另一焦点,若∠PF1Q= ,则双曲线的离心率等于( )(2)已知中心在原点,焦点在坐标轴上的双曲线的离心率等于 ,则其渐近线方程为 .?探究一探究二探究三当堂检测探究一探究二探究三当堂检测反思感悟双曲线的离心率与渐近线的求法及其关系
1.求双曲线的离心率,就是求a和c的值或a和c的关系,然后根据离心率的定义求得.但在多数情况下,由于受到题目已知条件的限制,很难或不可能求出a和c的值,只能将条件整理成关于a和c的关系式,进而求得 的值,其关键是善于利用定义以及图形中的几何关系来建立关于参数a,b,c的关系式,结合c2=a2+b2,化简为参数a,c的关系式进行求解.
2.双曲线的离心率与渐近线方程之间有着密切的联系,可以借助
进行互求.一般地,如果已知双曲线离心率的值求渐近线方程,或者已知渐近线方程,求离心率的值,都会有两解(焦点在x轴上和焦点在y轴上两种情况),不能忘记分类讨论.探究一探究二探究三当堂检测变式训练3(1)过双曲线 =1(a>0,b>0)的一个焦点F引它的一条渐近线的垂线FM,垂足为M,并且交y轴于点E,若M为EF的中点,则该双曲线的离心率为( )(2)已知直线2x-y+6=0过双曲线 =1(m>0)的一个焦点,则双曲线的渐近线方程为 .?探究一探究二探究三当堂检测探究一探究二探究三当堂检测思想方法
数学方法——双曲线离心率的常见求法
典例(1)若双曲线 =1(a>0,b>0)的一条渐近线经过点(3,-4),则此双曲线的离心率为( )(2)已知点A,B为双曲线E的左、右顶点,点M在双曲线E上,△ABM为等腰三角形,且顶角为120°,则双曲线E的离心率为( )探究一探究二探究三当堂检测答案(1)D (2)D 探究一探究二探究三当堂检测方法总结求双曲线离心率的方法 (3)若得到的是关于a,c的齐次方程pc2+qac+ra2=0(p,q,r为常数,且p≠0),则转化为关于e的方程pe2+qe+r=0求解.探究一探究二探究三当堂检测探究一探究二探究三当堂检测?探究一探究二探究三当堂检测1.双曲线 =1的左焦点与右顶点之间的距离等于( )
A.6 B.8 C.9 D.10
解析由已知得左焦点(-5,0),右顶点(3,0),所以左焦点与右顶点之间的距离等于8.
答案B
2.中心在原点,焦点在x轴上的双曲线的实轴与虚轴相等,一个焦点到一条渐近线的距离为 ,则双曲线方程为( )
A.x2-y2=1 B.x2-y2=2答案B 探究一探究二探究三当堂检测答案C 探究一探究二探究三当堂检测4.若双曲线 =-1的渐近线方程为y=±2x,则实数m等于 .?答案16 探究一探究二探究三当堂检测
(2)是不是轴对称图形?对称轴是哪条直线?是不是中心对称图形?对称中心是哪个点?答案(1)有限制,因为 ≥1,即x2≥a2,所以x≥a或x≤-a.
(2)关于x轴、y轴和原点都是对称的,x轴、y轴是双曲线的对称轴,原点是对称中心,又叫做双曲线的中心.双曲线的几何性质 名师点拨1.双曲线有“四点”(两个焦点、两个顶点),“四线”(两条对称轴、两条渐近线),椭圆是封闭性曲线,而双曲线是开放性曲线;双曲线有两支,故在应用时要注意点在哪一支上;根据方程判断焦点的位置时,注意双曲线与椭圆的差异性.
2.如果双曲线的方程确定,那么其渐近线的方程是唯一的,但如果双曲线的渐近线确定,那么其对应的双曲线有无数条,具有共同渐近线的双曲线方程可设为 =λ(λ≠0),当λ>0时,对应的双曲线焦点在x轴上,当λ<0时,对应的双曲线焦点在y轴上.【做一做1】 若点M(x0,y0)是双曲线 =1上支上的任意一点,则x0的取值范围是 ,y0的取值范围是 .?
解析因为a2=4,b2=25,所以a=2,b=5,所以x0∈R,y0≥2.
答案(-∞,+∞) [2,+∞)
【做一做2】 双曲线4x2-2y2=1的实轴长等于 ,虚轴长等于 ,焦距等于 .?探究一探究二探究三当堂检测 探究一双曲线的几何性质
例1 求双曲线9y2-4x2=-36的顶点坐标、焦点坐标、实轴长、虚轴长、离心率和渐近线方程.
思路分析将双曲线方程化为标准方程,先求出参数a,b,c的值,再写出各个结果.探究一探究二探究三当堂检测延伸探究若将方程9y2-4x2=-36改为9y2-4x2=36,其结果又将如何?探究一探究二探究三当堂检测反思感悟求双曲线的几何性质的基本思路
1.已知双曲线的方程研究其几何性质时,若不是标准方程,则应先化为标准方程,确定方程中a,b的对应值,利用c2=a2+b2得到c值,然后确定双曲线的焦点位置,从而写出它的几何性质.
2.求双曲线的渐近线方程时要特别注意焦点在x轴上还是在y轴上,以免写错.探究一探究二探究三当堂检测变式训练1(1)双曲线2x2-y2=-8的实轴长是 ( )答案(1)D (2)C 探究一探究二探究三当堂检测探究二根据双曲线几何性质求其标准方程
例2 求满足下列条件的双曲线的方程:
(1)已知双曲线的焦点在y轴上,实轴长与虚轴长之比为2∶3,且经过点P( ,2);
(2)已知双曲线的焦点在x轴上,离心率为 ,且经过点M(-3,2 );
(3)若双曲线的渐近线方程为2x±3y=0,且两顶点间的距离是6.
思路分析对于(1)和(2),可直接设出双曲线方程,根据条件求出参数a,b的值,即得方程;对于(3),焦点位置不确定,应分类讨论.探究一探究二探究三当堂检测探究一探究二探究三当堂检测探究一探究二探究三当堂检测反思感悟巧设双曲线方程的六种方法与技巧⑤渐近线为y=kx的双曲线方程可设为k2x2-y2=λ(λ≠0).
⑥渐近线为ax±by=0的双曲线方程可设为a2x2-b2y2=λ(λ≠0).探究一探究二探究三当堂检测变式训练2求满足下列条件的双曲线的标准方程:
(1)双曲线的实轴长与虚轴长之和等于其焦距的 倍,且一个顶点的坐标为(0,2);
(2)双曲线的渐近线方程为y=± x,且经过点A(2,-3).探究一探究二探究三当堂检测探究一探究二探究三当堂检测探究三双曲线的渐近线与离心率问题
例3 (1)过双曲线的一个焦点F2作垂直于实轴的弦PQ,F1是另一焦点,若∠PF1Q= ,则双曲线的离心率等于( )(2)已知中心在原点,焦点在坐标轴上的双曲线的离心率等于 ,则其渐近线方程为 .?探究一探究二探究三当堂检测探究一探究二探究三当堂检测反思感悟双曲线的离心率与渐近线的求法及其关系
1.求双曲线的离心率,就是求a和c的值或a和c的关系,然后根据离心率的定义求得.但在多数情况下,由于受到题目已知条件的限制,很难或不可能求出a和c的值,只能将条件整理成关于a和c的关系式,进而求得 的值,其关键是善于利用定义以及图形中的几何关系来建立关于参数a,b,c的关系式,结合c2=a2+b2,化简为参数a,c的关系式进行求解.
2.双曲线的离心率与渐近线方程之间有着密切的联系,可以借助
进行互求.一般地,如果已知双曲线离心率的值求渐近线方程,或者已知渐近线方程,求离心率的值,都会有两解(焦点在x轴上和焦点在y轴上两种情况),不能忘记分类讨论.探究一探究二探究三当堂检测变式训练3(1)过双曲线 =1(a>0,b>0)的一个焦点F引它的一条渐近线的垂线FM,垂足为M,并且交y轴于点E,若M为EF的中点,则该双曲线的离心率为( )(2)已知直线2x-y+6=0过双曲线 =1(m>0)的一个焦点,则双曲线的渐近线方程为 .?探究一探究二探究三当堂检测探究一探究二探究三当堂检测思想方法
数学方法——双曲线离心率的常见求法
典例(1)若双曲线 =1(a>0,b>0)的一条渐近线经过点(3,-4),则此双曲线的离心率为( )(2)已知点A,B为双曲线E的左、右顶点,点M在双曲线E上,△ABM为等腰三角形,且顶角为120°,则双曲线E的离心率为( )探究一探究二探究三当堂检测答案(1)D (2)D 探究一探究二探究三当堂检测方法总结求双曲线离心率的方法 (3)若得到的是关于a,c的齐次方程pc2+qac+ra2=0(p,q,r为常数,且p≠0),则转化为关于e的方程pe2+qe+r=0求解.探究一探究二探究三当堂检测探究一探究二探究三当堂检测?探究一探究二探究三当堂检测1.双曲线 =1的左焦点与右顶点之间的距离等于( )
A.6 B.8 C.9 D.10
解析由已知得左焦点(-5,0),右顶点(3,0),所以左焦点与右顶点之间的距离等于8.
答案B
2.中心在原点,焦点在x轴上的双曲线的实轴与虚轴相等,一个焦点到一条渐近线的距离为 ,则双曲线方程为( )
A.x2-y2=1 B.x2-y2=2答案B 探究一探究二探究三当堂检测答案C 探究一探究二探究三当堂检测4.若双曲线 =-1的渐近线方程为y=±2x,则实数m等于 .?答案16 探究一探究二探究三当堂检测
