高中数学新人教A版选修2-1课件:第二章圆锥曲线与方程2.4.2抛物线的简单几何性质(26张)
文档属性
| 名称 | 高中数学新人教A版选修2-1课件:第二章圆锥曲线与方程2.4.2抛物线的简单几何性质(26张) |  | |
| 格式 | zip | ||
| 文件大小 | 749.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-20 21:41:22 | ||
图片预览








文档简介
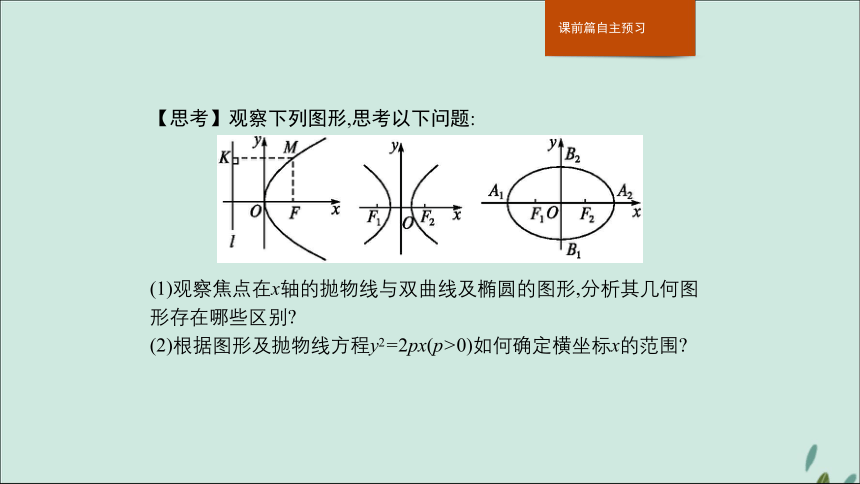
课件26张PPT。2.4.2 抛物线的简单几何性质【思考】观察下列图形,思考以下问题:
(1)观察焦点在x轴的抛物线与双曲线及椭圆的图形,分析其几何图形存在哪些区别?
(2)根据图形及抛物线方程y2=2px(p>0)如何确定横坐标x的范围?答案(1)抛物线与另两种曲线相比较,有明显的不同,椭圆是封闭曲线,有四个顶点,有两个焦点,有中心;双曲线虽然不是封闭曲线,但是有两支,有两个顶点,两个焦点,有中心;抛物线只有一条曲线,一个顶点,一个焦点,无中心.
(2)由抛物线y2=2px(p>0)有 所以x≥0.所以抛物线x的范围为x≥0.抛物线在y轴的右侧,当x的值增大时,|y|也增大,这说明抛物线向右上方和右下方无限延伸.1.抛物线的简单几何性质 名师点拨1.抛物线的几何性质与椭圆、双曲线相比有较大差别,它的离心率为定值1,只有一个焦点,一个顶点、一条对称轴、一条准线,没有渐近线,没有对称中心,通常称抛物线为无心圆锥曲线,而称椭圆、双曲线为有心圆锥曲线.
2.抛物线的焦点始终在对称轴上,抛物线的顶点就是抛物线与对称轴的交点,抛物线的准线始终与对称轴垂直,抛物线准线与对称轴的交点和焦点关于抛物线的顶点对称.【做一做1】 (1)顶点在原点,对称轴为y轴,顶点到准线的距离为4的抛物线方程是( )
A.x2=16y B.x2=8y
C.x2=±8y D.x2=±16y
(2)若点(a,b)是抛物线x2=2py(p>0)上的一点,则下列点一定在抛物线上的是( )
A.(a,-b) B.(-a,b)
C.(-a,-b) D.(b,a)
解析(1)由已知得 =4,2p=16,所以抛物线方程为x2=±16y.
(2)抛物线x2=2py关于y轴对称,所以点(a,b)关于y轴的对称点(-a,b)一定在抛物线上.
答案(1)D (2)B2.直线与抛物线的位置关系
设直线l:y=kx+m,抛物线:y2=2px(p>0),将直线方程与抛物线方程联立整理成关于x的方程k2x2+2(km-p)x+m2=0.
(1)若k≠0,当Δ>0时,直线与抛物线相交,有两个交点;
当Δ=0时,直线与抛物线相切,有一个切点;
当Δ<0时,直线与抛物线相离,没有公共点.
(2)若k=0,直线与抛物线有一个交点,此时直线平行于抛物线的对称轴或与对称轴重合.因此直线与抛物线有一个公共点是直线与抛物线相切的必要不充分条件.
特别提醒直线与抛物线相交时,直线与抛物线不一定有两个公共点;直线与抛物线只有一个公共点时,直线与抛物线不一定相切,也有可能是相交,这时直线与抛物线的对称轴平行.【做一做2】 (1)直线y=2x-1与抛物线x2= y的位置关系是( )
A.相切 B.相交
C.相离 D.不确定
(2)过点(1,1)与抛物线y2=x只有一个公共点的直线有( )
A.1条 B.2条 C.3条 D.4条因为Δ=-1<0,所以直线与抛物线相离.
(2)因为点(1,1)在抛物线y2=x上,所以与y2=x只有一个公共点的直线有两条,其中一条为切线,一条为平行于x轴的直线.
答案(1)C (2)B探究一探究二探究三当堂检测 探究一由抛物线的几何性质求标准方程
例1 抛物线的顶点在原点,对称轴重合于椭圆9x2+4y2=36短轴所在的直线,抛物线焦点到顶点的距离为3,求抛物线的方程及抛物线的准线方程.
解椭圆的方程可化为 =1,其短轴在x轴上,
∴抛物线的对称轴为x轴,
∴设抛物线的方程为y2=2px或y2=-2px(p>0).
∵抛物线的焦点到顶点的距离为3,即 =3,∴p=6.
∴抛物线的标准方程为y2=12x或y2=-12x,
其准线方程分别为x=-3或x=3.探究一探究二探究三当堂检测反思感悟抛物线各元素间的关系
抛物线的焦点始终在对称轴上,顶点就是抛物线与对称轴的交点,准线始终与对称轴垂直,准线与对称轴的交点和焦点关于顶点对称,顶点到焦点的距离等于顶点到准线的距离为 .探究一探究二探究三当堂检测延伸探究抛物线的顶点在原点,对称轴重合于双曲线9x2-4y2=36虚轴所在的直线,其他条件不变,抛物线的方程如何?
解双曲线9x2-4y2=36的虚轴为y轴,
∴抛物线的对称轴为y轴,
∴设抛物线的方程为x2=2py或x2=-2py(p>0).
∵抛物线的焦点到顶点的距离为3,即 =3,∴p=6.
∴抛物线的标准方程为x2=12y或x2=-12y.探究一探究二探究三当堂检测变式训练1边长为1的等边三角形AOB,O为坐标原点,AB⊥x轴,以O为顶点且过A,B的抛物线方程是 ( )答案C 探究一探究二探究三当堂检测探究二直线与抛物线的位置关系
例2 已知直线l:y=kx+1,抛物线C:y2=4x,当k为何值时,l与C有:
(1)一个公共点;(2)两个公共点;(3)没有公共点?
思路分析将直线方程与抛物线方程联立,消去y得到关于x的方程后,讨论根的情况,得到公共点的个数情况.探究一探究二探究三当堂检测当k≠0时,方程(*)是一个一元二次方程,且Δ=(2k-4)2-4k2×1=16-16k,
①当Δ>0,即k<1,且k≠0时,l与C有两个公共点,此时l与C相交;
②当Δ=0,即k=1时,l与C有一个公共点,此时直线l与C相切;
③当Δ<0时,即k>1时,l与C没有公共点,此时直线l与C相离.
综上所述,(1)当k=1或k=0时,直线l与C有一个公共点;
(2)当k<1,且k≠0时,直线l与C有两个公共点;
(3)当k>1时,直线l与C没有公共点.探究一探究二探究三当堂检测反思感悟方程思想解决直线与抛物线的位置关系
研究直线与抛物线的位置关系问题主要采用代数方法,即当直线斜率存在时,设直线l的方程为y=kx+m,抛物线的方程为y2=2px(p>0),将直线方程与抛物线方程联立整理成关于x(或y)的一元二次方程形式Ax2+Bx+C=0(或Ay2+By+C=0).探究一探究二探究三当堂检测变式训练2设抛物线y2=8x的准线与x轴交于点Q,若过点Q的直线l与抛物线有公共点,则直线l的斜率的取值范围是( )解析设直线方程为y=k(x+2),与抛物线方程联立,整理得ky2-8y+16k=0.当k=0时,直线与抛物线有一个交点;当k≠0时,由Δ=64-64k2≥0,解得-1≤k≤1,所以-1≤k≤1.
答案C探究一探究二探究三当堂检测探究三抛物线在实际问题中的应用
例3 如图所示,花坛水池中央有一喷泉,水管O'P=1 m,水从喷头P喷出后呈抛物线状,先向上至最高点后落下,若最高点距水面2 m,点P距抛物线的对称轴1 m,则水池的直径至少应设计多少米?(精确到1 m)
思路分析以抛物线的顶点为原点,对称轴为y轴建立平面直角坐标系,则易得点P的坐标,再由P在抛物线上求出抛物线方程,设抛物线与水面的交点为B,则由点B的纵坐标求出点B的横坐标即可得解.探究一探究二探究三当堂检测解如图所示,建立平面直角坐标系.
设抛物线方程为x2=-2py(p>0).
依题意有P(-1,-1)在抛物线上,代入得p= .
故得抛物线方程为x2=-y.反思感悟坐标法解决与抛物线有关的实际问题
解决实际问题时,首先找到合适的数学模型,把它转化为数学问题,通过我们学过的数学知识进行求解.利用抛物线模型解决问题时,关键是建立坐标系得到抛物线的标准方程,一般都是将抛物线的顶点作为坐标原点,将对称轴作为x轴或y轴建立坐标系,其次要注意抛物线上关键点的坐标,并善于运用抛物线的对称性进行求解.探究一探究二探究三当堂检测变式训练3如图是抛物线形拱桥,当水面到直线l时,拱顶离水面2 m,水面宽为4 m.水位下降1 m后,水面宽为 m.解析建立如图所示的平面直角坐标系.
设抛物线的方程为x2=-2py(p>0),由点(2,-2)在抛物线上,可得p=1,则抛物线方程为x2=-2y.当y=-3时,x=± ,故水面宽为2 m.
答案2探究一探究二探究三当堂检测思维辨析
一题多解——与中点弦有关的问题
典例过点Q(4,1)作抛物线y2=8x的弦AB,恰被点Q所平分,则AB所在直线的方程为 .?
思路分析法一:设A(x1,y1),B(x2,y2),用点差法求kAB;法二:设直线AB的方程,建立方程求解.解析(1)法一:设以Q为中点的弦AB的端点坐标为∴(y1+y2)(y1-y2)=8(x1-x2).
又y1+y2=2,∴y1-y2=4(x1-x2),∴所求弦AB所在直线的方程为y-1=4(x-4),
即4x-y-15=0.探究一探究二探究三当堂检测法二:设弦AB所在直线的方程为y=k(x-4)+1.联立
消去x,得ky2-8y-32k+8=0,此方程的两根就是线段端点A,B两点的纵坐标,
由根与系数得y1+y2= .
又y1+y2=2,∴k=4.
∴所求弦AB所在直线的方程为4x-y-15=0.
答案4x-y-15=0探究一探究二探究三当堂检测1.抛物线C:y2=2px(p>0)的焦点F到准线l的距离为2,则C的焦点坐标为( )解析∵焦点F到准线l的距离为2,∴p=2.抛物线方程为y2=4x,∴焦点F的坐标为(1,0).故选C.
答案C探究一探究二探究三当堂检测2.直线y=2x+4与抛物线y=x2交于A,B两点,则△ABO的面积为( )答案B 探究一探究二探究三当堂检测3.若抛物线x2=ay的焦点到准线的距离为1,则a= ( )
A.2 B.4
C.±2 D.±4答案C 探究一探究二探究三当堂检测4.如图所示,等边三角形OAB的边长为8 ,且其三个顶点均在抛物线E:x2=2py(p>0)上,求抛物线E的方程.
(1)观察焦点在x轴的抛物线与双曲线及椭圆的图形,分析其几何图形存在哪些区别?
(2)根据图形及抛物线方程y2=2px(p>0)如何确定横坐标x的范围?答案(1)抛物线与另两种曲线相比较,有明显的不同,椭圆是封闭曲线,有四个顶点,有两个焦点,有中心;双曲线虽然不是封闭曲线,但是有两支,有两个顶点,两个焦点,有中心;抛物线只有一条曲线,一个顶点,一个焦点,无中心.
(2)由抛物线y2=2px(p>0)有 所以x≥0.所以抛物线x的范围为x≥0.抛物线在y轴的右侧,当x的值增大时,|y|也增大,这说明抛物线向右上方和右下方无限延伸.1.抛物线的简单几何性质 名师点拨1.抛物线的几何性质与椭圆、双曲线相比有较大差别,它的离心率为定值1,只有一个焦点,一个顶点、一条对称轴、一条准线,没有渐近线,没有对称中心,通常称抛物线为无心圆锥曲线,而称椭圆、双曲线为有心圆锥曲线.
2.抛物线的焦点始终在对称轴上,抛物线的顶点就是抛物线与对称轴的交点,抛物线的准线始终与对称轴垂直,抛物线准线与对称轴的交点和焦点关于抛物线的顶点对称.【做一做1】 (1)顶点在原点,对称轴为y轴,顶点到准线的距离为4的抛物线方程是( )
A.x2=16y B.x2=8y
C.x2=±8y D.x2=±16y
(2)若点(a,b)是抛物线x2=2py(p>0)上的一点,则下列点一定在抛物线上的是( )
A.(a,-b) B.(-a,b)
C.(-a,-b) D.(b,a)
解析(1)由已知得 =4,2p=16,所以抛物线方程为x2=±16y.
(2)抛物线x2=2py关于y轴对称,所以点(a,b)关于y轴的对称点(-a,b)一定在抛物线上.
答案(1)D (2)B2.直线与抛物线的位置关系
设直线l:y=kx+m,抛物线:y2=2px(p>0),将直线方程与抛物线方程联立整理成关于x的方程k2x2+2(km-p)x+m2=0.
(1)若k≠0,当Δ>0时,直线与抛物线相交,有两个交点;
当Δ=0时,直线与抛物线相切,有一个切点;
当Δ<0时,直线与抛物线相离,没有公共点.
(2)若k=0,直线与抛物线有一个交点,此时直线平行于抛物线的对称轴或与对称轴重合.因此直线与抛物线有一个公共点是直线与抛物线相切的必要不充分条件.
特别提醒直线与抛物线相交时,直线与抛物线不一定有两个公共点;直线与抛物线只有一个公共点时,直线与抛物线不一定相切,也有可能是相交,这时直线与抛物线的对称轴平行.【做一做2】 (1)直线y=2x-1与抛物线x2= y的位置关系是( )
A.相切 B.相交
C.相离 D.不确定
(2)过点(1,1)与抛物线y2=x只有一个公共点的直线有( )
A.1条 B.2条 C.3条 D.4条因为Δ=-1<0,所以直线与抛物线相离.
(2)因为点(1,1)在抛物线y2=x上,所以与y2=x只有一个公共点的直线有两条,其中一条为切线,一条为平行于x轴的直线.
答案(1)C (2)B探究一探究二探究三当堂检测 探究一由抛物线的几何性质求标准方程
例1 抛物线的顶点在原点,对称轴重合于椭圆9x2+4y2=36短轴所在的直线,抛物线焦点到顶点的距离为3,求抛物线的方程及抛物线的准线方程.
解椭圆的方程可化为 =1,其短轴在x轴上,
∴抛物线的对称轴为x轴,
∴设抛物线的方程为y2=2px或y2=-2px(p>0).
∵抛物线的焦点到顶点的距离为3,即 =3,∴p=6.
∴抛物线的标准方程为y2=12x或y2=-12x,
其准线方程分别为x=-3或x=3.探究一探究二探究三当堂检测反思感悟抛物线各元素间的关系
抛物线的焦点始终在对称轴上,顶点就是抛物线与对称轴的交点,准线始终与对称轴垂直,准线与对称轴的交点和焦点关于顶点对称,顶点到焦点的距离等于顶点到准线的距离为 .探究一探究二探究三当堂检测延伸探究抛物线的顶点在原点,对称轴重合于双曲线9x2-4y2=36虚轴所在的直线,其他条件不变,抛物线的方程如何?
解双曲线9x2-4y2=36的虚轴为y轴,
∴抛物线的对称轴为y轴,
∴设抛物线的方程为x2=2py或x2=-2py(p>0).
∵抛物线的焦点到顶点的距离为3,即 =3,∴p=6.
∴抛物线的标准方程为x2=12y或x2=-12y.探究一探究二探究三当堂检测变式训练1边长为1的等边三角形AOB,O为坐标原点,AB⊥x轴,以O为顶点且过A,B的抛物线方程是 ( )答案C 探究一探究二探究三当堂检测探究二直线与抛物线的位置关系
例2 已知直线l:y=kx+1,抛物线C:y2=4x,当k为何值时,l与C有:
(1)一个公共点;(2)两个公共点;(3)没有公共点?
思路分析将直线方程与抛物线方程联立,消去y得到关于x的方程后,讨论根的情况,得到公共点的个数情况.探究一探究二探究三当堂检测当k≠0时,方程(*)是一个一元二次方程,且Δ=(2k-4)2-4k2×1=16-16k,
①当Δ>0,即k<1,且k≠0时,l与C有两个公共点,此时l与C相交;
②当Δ=0,即k=1时,l与C有一个公共点,此时直线l与C相切;
③当Δ<0时,即k>1时,l与C没有公共点,此时直线l与C相离.
综上所述,(1)当k=1或k=0时,直线l与C有一个公共点;
(2)当k<1,且k≠0时,直线l与C有两个公共点;
(3)当k>1时,直线l与C没有公共点.探究一探究二探究三当堂检测反思感悟方程思想解决直线与抛物线的位置关系
研究直线与抛物线的位置关系问题主要采用代数方法,即当直线斜率存在时,设直线l的方程为y=kx+m,抛物线的方程为y2=2px(p>0),将直线方程与抛物线方程联立整理成关于x(或y)的一元二次方程形式Ax2+Bx+C=0(或Ay2+By+C=0).探究一探究二探究三当堂检测变式训练2设抛物线y2=8x的准线与x轴交于点Q,若过点Q的直线l与抛物线有公共点,则直线l的斜率的取值范围是( )解析设直线方程为y=k(x+2),与抛物线方程联立,整理得ky2-8y+16k=0.当k=0时,直线与抛物线有一个交点;当k≠0时,由Δ=64-64k2≥0,解得-1≤k≤1,所以-1≤k≤1.
答案C探究一探究二探究三当堂检测探究三抛物线在实际问题中的应用
例3 如图所示,花坛水池中央有一喷泉,水管O'P=1 m,水从喷头P喷出后呈抛物线状,先向上至最高点后落下,若最高点距水面2 m,点P距抛物线的对称轴1 m,则水池的直径至少应设计多少米?(精确到1 m)
思路分析以抛物线的顶点为原点,对称轴为y轴建立平面直角坐标系,则易得点P的坐标,再由P在抛物线上求出抛物线方程,设抛物线与水面的交点为B,则由点B的纵坐标求出点B的横坐标即可得解.探究一探究二探究三当堂检测解如图所示,建立平面直角坐标系.
设抛物线方程为x2=-2py(p>0).
依题意有P(-1,-1)在抛物线上,代入得p= .
故得抛物线方程为x2=-y.反思感悟坐标法解决与抛物线有关的实际问题
解决实际问题时,首先找到合适的数学模型,把它转化为数学问题,通过我们学过的数学知识进行求解.利用抛物线模型解决问题时,关键是建立坐标系得到抛物线的标准方程,一般都是将抛物线的顶点作为坐标原点,将对称轴作为x轴或y轴建立坐标系,其次要注意抛物线上关键点的坐标,并善于运用抛物线的对称性进行求解.探究一探究二探究三当堂检测变式训练3如图是抛物线形拱桥,当水面到直线l时,拱顶离水面2 m,水面宽为4 m.水位下降1 m后,水面宽为 m.解析建立如图所示的平面直角坐标系.
设抛物线的方程为x2=-2py(p>0),由点(2,-2)在抛物线上,可得p=1,则抛物线方程为x2=-2y.当y=-3时,x=± ,故水面宽为2 m.
答案2探究一探究二探究三当堂检测思维辨析
一题多解——与中点弦有关的问题
典例过点Q(4,1)作抛物线y2=8x的弦AB,恰被点Q所平分,则AB所在直线的方程为 .?
思路分析法一:设A(x1,y1),B(x2,y2),用点差法求kAB;法二:设直线AB的方程,建立方程求解.解析(1)法一:设以Q为中点的弦AB的端点坐标为∴(y1+y2)(y1-y2)=8(x1-x2).
又y1+y2=2,∴y1-y2=4(x1-x2),∴所求弦AB所在直线的方程为y-1=4(x-4),
即4x-y-15=0.探究一探究二探究三当堂检测法二:设弦AB所在直线的方程为y=k(x-4)+1.联立
消去x,得ky2-8y-32k+8=0,此方程的两根就是线段端点A,B两点的纵坐标,
由根与系数得y1+y2= .
又y1+y2=2,∴k=4.
∴所求弦AB所在直线的方程为4x-y-15=0.
答案4x-y-15=0探究一探究二探究三当堂检测1.抛物线C:y2=2px(p>0)的焦点F到准线l的距离为2,则C的焦点坐标为( )解析∵焦点F到准线l的距离为2,∴p=2.抛物线方程为y2=4x,∴焦点F的坐标为(1,0).故选C.
答案C探究一探究二探究三当堂检测2.直线y=2x+4与抛物线y=x2交于A,B两点,则△ABO的面积为( )答案B 探究一探究二探究三当堂检测3.若抛物线x2=ay的焦点到准线的距离为1,则a= ( )
A.2 B.4
C.±2 D.±4答案C 探究一探究二探究三当堂检测4.如图所示,等边三角形OAB的边长为8 ,且其三个顶点均在抛物线E:x2=2py(p>0)上,求抛物线E的方程.
