高中数学新人教A版选修2-1课件:第三章空间向量与立体几何3.1.1空间向量及其加减运算(26张)
文档属性
| 名称 | 高中数学新人教A版选修2-1课件:第三章空间向量与立体几何3.1.1空间向量及其加减运算(26张) |

|
|
| 格式 | zip | ||
| 文件大小 | 710.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-20 00:00:00 | ||
图片预览








文档简介
课件26张PPT。第三章 空间向量与立体几何3.1 空间向量及其运算3.1.1 空间向量及其加减运算【思考1】类比平面向量的概念,能否给出空间向量的概念?
答案能.在空间,把具有大小和方向的量叫做空间向量.
1.空间向量及其表示
(1)定义:在空间,把具有大小和方向的量叫做空间向量.向量的大小叫做向量的长度或模.
(2)表示:①几何表示法,用有向线段表示;
②字母表示法,用a,b,c,…表示或用表示向量的有向线段的起点和终点的字母表示.特别提醒注意区分有向线段与向量.向量可用有向线段来表示,但是有向线段不是向量,它只是向量的一种表示方法.2.空间向量的相关概念
(1)零向量:长度为0的向量叫做零向量,记为0.
(2)单位向量:模为1的向量称为单位向量.
(3)相反向量:与向量a长度相等而方向相反的向量称为a的相反向量,记为-a.
(4)相等向量:方向相同且模相等的向量称为相等向量.
名师点拨1.空间向量的表示方法,以及零向量、单位向量、相等向量、相反向量等概念与平面向量相同.
2.凡涉及空间两个向量的问题,平面向量中有关结论仍然适用它们.
3.两个向量的关系:空间向量是具有大小与方向的量,两个向量只有相等与不相等之分,而无大小之分.【做一做1】 下列命题正确的是( )
A.若向量a与b的方向相反,则称向量a与b为相反向量
B.零向量没有方向
C.若a是单位向量,则|a|=1
D.若向量m,n,p满足m=n,n=p,则不一定有m=p
解析单位向量是指模等于1的向量,所以若a是单位向量,则必有|a|=1,即C项正确.
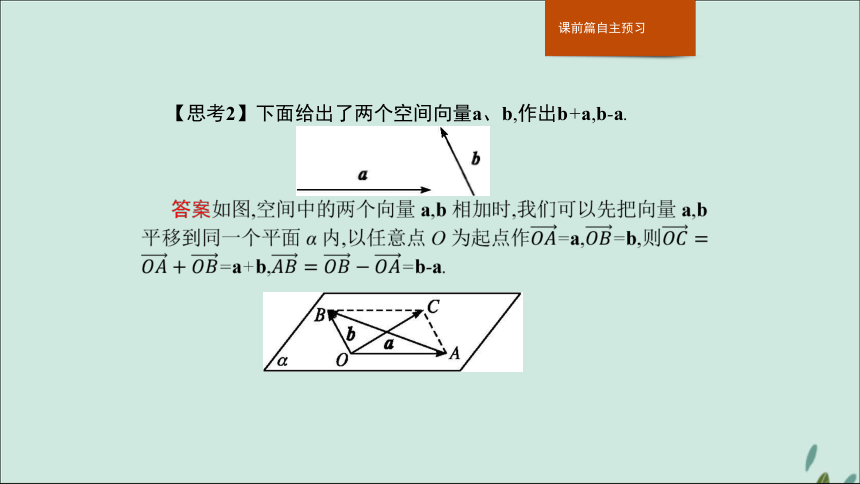
答案C【思考2】下面给出了两个空间向量a、b,作出b+a,b-a.3.空间向量的加减运算及其运算律 特别提醒1.首尾相接的若干向量之和等于由起始向量的起点指向末尾向量的终点的向量.
2.首尾相接的若干向量若构成一个封闭图形,则它们的和是零向量.A.a+b-c B.c-a-b
C.c+a-b D.c+a+b答案B 探究一探究二当堂检测探究一空间向量及相关概念的理解 探究一探究二当堂检测解析①错误,在同一条直线上的单位向量,方向可能相同,也可能相反,故它们不一定相等;
②正确,零向量的模等于0,模等于0的向量只有零向量;答案②③ 探究一探究二当堂检测反思感悟空间向量概念的辨析
(1)向量的两个要素是大小与方向,两者缺一不可;
(2)单位向量的方向虽然不一定相同,但长度一定为1;
(3)两个向量的模相等,则它们的长度相等,但方向不确定,即两个向量(非零向量)的模相等是两个向量相等的必要不充分条件;
(4)由于方向不能比较大小,因此“大于”“小于”对向量来说是没有意义的,但向量的模是可以比较大小的.探究一探究二当堂检测变式训练1下列说法正确的是( )
A.若|a|=|b|,则a,b的长度相同,方向相同或相反
B.若向量a是向量b的相反向量,则|a|=|b|
C.两个向量相等,若它们的起点相同,则其终点不一定相同
D.若|a|>|b|,|b|>|c|,则a>c
解析两个向量是相反向量时,它们的模必相等,故B项正确.
答案B探究一探究二当堂检测探究二空间向量的加法与减法运算
例2 如图,已知长方体ABCD-A'B'C'D',化简下列向量表达式,并在图中标出化简结果的向量.思路分析根据空间向量加法及减法运算法则求解.探究一探究二当堂检测反思感悟1.空间向量加法、减法运算的两个技巧
(1)巧用相反向量:向量加减法的三角形法则是解决空间向量加法、减法运算的关键,灵活应用相反向量可使有关向量首尾相接,从而便于运算.
(2)巧用平移:利用三角形法则和平行四边形法则进行向量的加法运算时,务必要注意和向量、差向量的方向,必要时可采用空间向量的自由平移获得更准确的结果.
2.化简空间向量的常用思路
(1)分组:合理分组,以便灵活运用三角形法则、平行四边形法则进行化简.
(2)多边形法则:在空间向量的加法运算中,若是多个向量求和,还可利用多边形法则,若干个向量的和可以将其转化为首尾相接的向量求和.
(3)走边路:灵活运用空间向量的加法、减法法则,尽量走边路(即沿几何体的边选择途径).探究一探究二当堂检测探究一探究二当堂检测思维辨析
一题多变——空间向量的加法、减法运算探究一探究二当堂检测探究一探究二当堂检测解(1)根据六棱柱的性质知四边形BB1C1C,DD1E1E都是平行四边形,探究一探究二当堂检测(2)因为六边形ABCDEF是正六边形,
所以BC∥EF,BC=EF,
又因为E1F1∥EF,E1F1=EF,
所以BC∥E1F1,BC=E1F1,
所以BCE1F1是平行四边形,方法总结在进行减法运算时,可将减去一个向量转化为加上这个向量的相反向量,而在进行加法运算时,首先考虑这两个向量在哪个平面内,然后与平面向量求和一样,运用向量运算的平行四边形法则、三角形法则及多边形法则来求.探究一探究二当堂检测1.“两个非零空间向量的模相等”是“两个空间向量相等”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
解析两个向量相等是指两个向量的模相等并且方向相同,因此“两个非零向量的模相等”是“两个向量相等”的必要不充分条件.
答案B探究一探究二当堂检测答案C 探究一探究二当堂检测3.在平行六面体ABCD-A'B'C'D'中,与向量 相等的向量共有( )
A.1个 B.2个 C.3个 D.4个答案C 解析如图, 答案-c-a+b 探究一探究二当堂检测5.如图所示的是平行六面体ABCD-A1B1C1D1,化简下列各式.
答案能.在空间,把具有大小和方向的量叫做空间向量.
1.空间向量及其表示
(1)定义:在空间,把具有大小和方向的量叫做空间向量.向量的大小叫做向量的长度或模.
(2)表示:①几何表示法,用有向线段表示;
②字母表示法,用a,b,c,…表示或用表示向量的有向线段的起点和终点的字母表示.特别提醒注意区分有向线段与向量.向量可用有向线段来表示,但是有向线段不是向量,它只是向量的一种表示方法.2.空间向量的相关概念
(1)零向量:长度为0的向量叫做零向量,记为0.
(2)单位向量:模为1的向量称为单位向量.
(3)相反向量:与向量a长度相等而方向相反的向量称为a的相反向量,记为-a.
(4)相等向量:方向相同且模相等的向量称为相等向量.
名师点拨1.空间向量的表示方法,以及零向量、单位向量、相等向量、相反向量等概念与平面向量相同.
2.凡涉及空间两个向量的问题,平面向量中有关结论仍然适用它们.
3.两个向量的关系:空间向量是具有大小与方向的量,两个向量只有相等与不相等之分,而无大小之分.【做一做1】 下列命题正确的是( )
A.若向量a与b的方向相反,则称向量a与b为相反向量
B.零向量没有方向
C.若a是单位向量,则|a|=1
D.若向量m,n,p满足m=n,n=p,则不一定有m=p
解析单位向量是指模等于1的向量,所以若a是单位向量,则必有|a|=1,即C项正确.
答案C【思考2】下面给出了两个空间向量a、b,作出b+a,b-a.3.空间向量的加减运算及其运算律 特别提醒1.首尾相接的若干向量之和等于由起始向量的起点指向末尾向量的终点的向量.
2.首尾相接的若干向量若构成一个封闭图形,则它们的和是零向量.A.a+b-c B.c-a-b
C.c+a-b D.c+a+b答案B 探究一探究二当堂检测探究一空间向量及相关概念的理解 探究一探究二当堂检测解析①错误,在同一条直线上的单位向量,方向可能相同,也可能相反,故它们不一定相等;
②正确,零向量的模等于0,模等于0的向量只有零向量;答案②③ 探究一探究二当堂检测反思感悟空间向量概念的辨析
(1)向量的两个要素是大小与方向,两者缺一不可;
(2)单位向量的方向虽然不一定相同,但长度一定为1;
(3)两个向量的模相等,则它们的长度相等,但方向不确定,即两个向量(非零向量)的模相等是两个向量相等的必要不充分条件;
(4)由于方向不能比较大小,因此“大于”“小于”对向量来说是没有意义的,但向量的模是可以比较大小的.探究一探究二当堂检测变式训练1下列说法正确的是( )
A.若|a|=|b|,则a,b的长度相同,方向相同或相反
B.若向量a是向量b的相反向量,则|a|=|b|
C.两个向量相等,若它们的起点相同,则其终点不一定相同
D.若|a|>|b|,|b|>|c|,则a>c
解析两个向量是相反向量时,它们的模必相等,故B项正确.
答案B探究一探究二当堂检测探究二空间向量的加法与减法运算
例2 如图,已知长方体ABCD-A'B'C'D',化简下列向量表达式,并在图中标出化简结果的向量.思路分析根据空间向量加法及减法运算法则求解.探究一探究二当堂检测反思感悟1.空间向量加法、减法运算的两个技巧
(1)巧用相反向量:向量加减法的三角形法则是解决空间向量加法、减法运算的关键,灵活应用相反向量可使有关向量首尾相接,从而便于运算.
(2)巧用平移:利用三角形法则和平行四边形法则进行向量的加法运算时,务必要注意和向量、差向量的方向,必要时可采用空间向量的自由平移获得更准确的结果.
2.化简空间向量的常用思路
(1)分组:合理分组,以便灵活运用三角形法则、平行四边形法则进行化简.
(2)多边形法则:在空间向量的加法运算中,若是多个向量求和,还可利用多边形法则,若干个向量的和可以将其转化为首尾相接的向量求和.
(3)走边路:灵活运用空间向量的加法、减法法则,尽量走边路(即沿几何体的边选择途径).探究一探究二当堂检测探究一探究二当堂检测思维辨析
一题多变——空间向量的加法、减法运算探究一探究二当堂检测探究一探究二当堂检测解(1)根据六棱柱的性质知四边形BB1C1C,DD1E1E都是平行四边形,探究一探究二当堂检测(2)因为六边形ABCDEF是正六边形,
所以BC∥EF,BC=EF,
又因为E1F1∥EF,E1F1=EF,
所以BC∥E1F1,BC=E1F1,
所以BCE1F1是平行四边形,方法总结在进行减法运算时,可将减去一个向量转化为加上这个向量的相反向量,而在进行加法运算时,首先考虑这两个向量在哪个平面内,然后与平面向量求和一样,运用向量运算的平行四边形法则、三角形法则及多边形法则来求.探究一探究二当堂检测1.“两个非零空间向量的模相等”是“两个空间向量相等”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
解析两个向量相等是指两个向量的模相等并且方向相同,因此“两个非零向量的模相等”是“两个向量相等”的必要不充分条件.
答案B探究一探究二当堂检测答案C 探究一探究二当堂检测3.在平行六面体ABCD-A'B'C'D'中,与向量 相等的向量共有( )
A.1个 B.2个 C.3个 D.4个答案C 解析如图, 答案-c-a+b 探究一探究二当堂检测5.如图所示的是平行六面体ABCD-A1B1C1D1,化简下列各式.
