高中数学新人教A版选修2-1课件:第一章常用逻辑用语1.1.2四种命题1.1.3四种命题间的相互关系(25张)
文档属性
| 名称 | 高中数学新人教A版选修2-1课件:第一章常用逻辑用语1.1.2四种命题1.1.3四种命题间的相互关系(25张) |

|
|
| 格式 | zip | ||
| 文件大小 | 275.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-20 21:44:22 | ||
图片预览







文档简介
课件25张PPT。1.1.2~1.1.3 四种命题 四种命题间的相互关系【思考】初中已学过命题与逆命题的知识,什么叫做命题的逆命题?
答案在两个命题中,如果第一个命题的条件是第二个命题的结论,且第一个命题的结论是第二个命题的条件,那么这两个命题叫做互为逆命题,其中一个叫做原命题,另一个叫做原命题的逆命题.1.四种命题
(1)逆命题
对于两个命题,如果一个命题的条件和结论分别为另一个命题的结论和条件,那么我们把这样的两个命题叫做互逆命题,其中一个叫做原命题,另一个叫做原命题的逆命题.如果原命题为“若p,则q”,则其逆命题为“若q,则p”.
(2)否命题
对于两个命题,如果一个命题的条件和结论分别为另一个命题的条件的否定和结论的否定,那么我们把这样的两个命题叫做互否命题,其中一个叫做原命题,另一个叫做原命题的否命题.如果原命题为“若p,则q”,那么其否命题为“若??p,则??q”.
(3)逆否命题
对于两个命题,如果一个命题的条件和结论分别为另一个命题的结论的否定和条件的否定,那么我们把这样的两个命题叫做互为逆否命题,其中一个叫做原命题,另一个叫做原命题的逆否命题.如果原命题为“若p,则q”,那么其逆否命题为“若??q,则??p”.名师点拨1.四种命题中的任何一个都可以作为原命题,即命题的四种形式中,原命题是不确定的.
2.“互为逆否命题”与“逆否命题”是不同的,互为逆否命题指的是两个命题之间的关系,具有双向性,而逆否命题指的是一个命题,具有单向性.【做一做1】 已知命题p:若x=y,则cos x=cos y,则命题p的逆命题为 ;命题p的否命题为 ;命题p的逆否命题为 .?
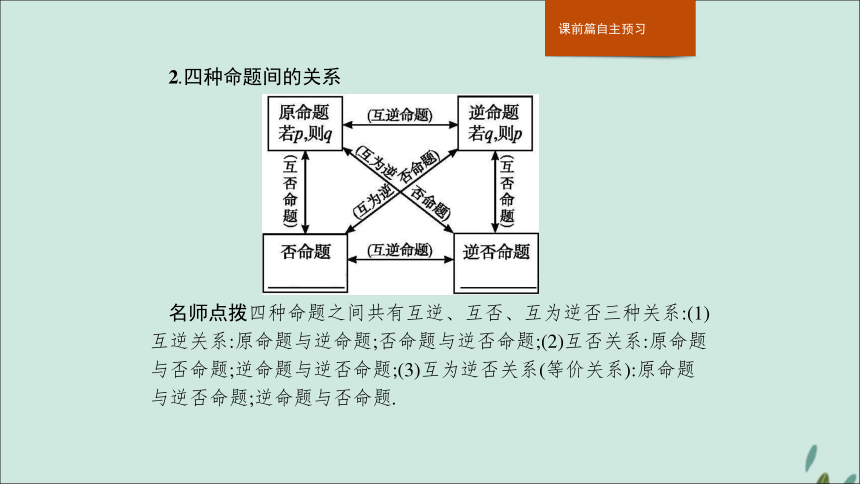
答案若cos x=cos y,则x=y 若x≠y,则cos x≠cos y 若cos x≠cos y,则x≠y2.四种命题间的关系 名师点拨四种命题之间共有互逆、互否、互为逆否三种关系:(1)互逆关系:原命题与逆命题;否命题与逆否命题;(2)互否关系:原命题与否命题;逆命题与逆否命题;(3)互为逆否关系(等价关系):原命题与逆否命题;逆命题与否命题.【做一做2】 给出以下命题:
①若一个四边形的四条边不相等,则它不是正方形;②若一个四边形对角互补,则它内接于圆;③正方形的四条边相等;④圆内接四边形对角互补;⑤对角不互补的四边形不内接于圆;⑥若一个四边形的边相等,则它是正方形.
其中互为逆命题的有 ;互为否命题的有 ;互为逆否命题的有 .?
解析命题③可改写为“若一个四边形是正方形,则它的四条边相等”;命题④可改写为“若一个四边形是圆内接四边形,则它的对角互补”;命题⑤可改写为“若一个四边形的对角不互补,则它不内接于圆”.因此互为逆命题的有③和⑥,②和④;互为否命题的有①和⑥,②和⑤;互为逆否命题的有①和③,④和⑤.
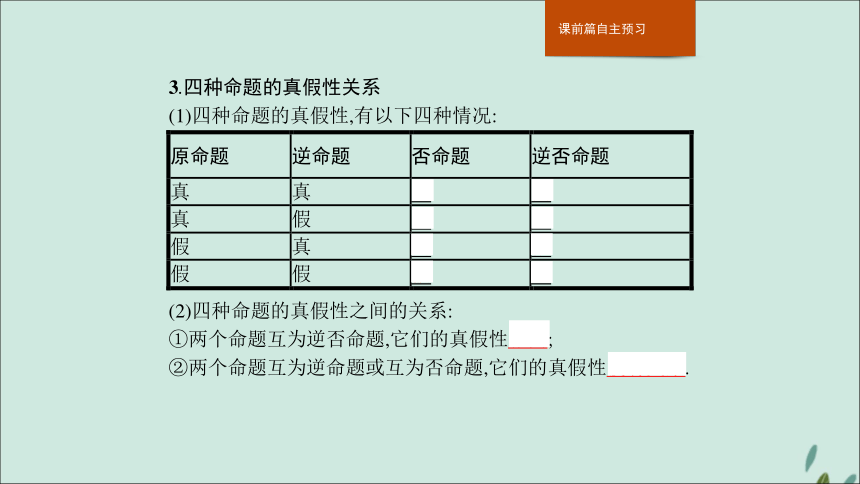
答案③和⑥,②和④ ①和⑥,②和⑤ ①和③,④和⑤3.四种命题的真假性关系
(1)四种命题的真假性,有以下四种情况:(2)四种命题的真假性之间的关系:
①两个命题互为逆否命题,它们的真假性相同;
②两个命题互为逆命题或互为否命题,它们的真假性没有关系.【做一做3】 命题“若a>-3,则a>-6”以及它的逆命题、否命题、逆否命题中,真命题的个数为( )
A.1 B.2
C.3 D.4
解析由a>-3可得a>-6,但由a>-6得不出a>-3,故原命题及原命题的逆否命题为真命题.
答案B探究一探究二当堂检测 探究一命题的四种形式
例1 写出下列各个命题的逆命题、否命题以及逆否命题.
(1)若sin α= ,则tan α= ;
(2)等底等高的两个三角形是全等三角形;
(3)当1(4)若ab=0,则a=0或b=0.探究一探究二当堂检测(2)逆命题:若两个三角形全等,则这两个三角形等底等高.
否命题:若两个三角形不等底或不等高,则这两个三角形不全等.
逆否命题:若两个三角形不全等,则这两个三角形不等底或不等高.
(3)逆命题:若x2-3x+2<0,则1否命题:若x≤1或x≥2,则x2-3x+2≥0.
逆否命题:若x2-3x+2≥0,则x≤1或x≥2.
(4)逆命题:若a=0或b=0,则ab=0.
否命题:若ab≠0,则a≠0,且b≠0.
逆否命题:若a≠0,且b≠0,则ab≠0.探究一探究二当堂检测反思感悟四种命题的写法及注意事项
1.给出一个命题,写出其命题的四种形式时,首先要弄清楚该命题的条件和结论,若给出的命题不是“若p,则q”的形式,则应改写为“若p,则q”的形式,找出命题的条件和结论.
2.由原命题“若p,则q”写其他三种命题的方法:
(1)“换位”(即交换命题的条件与结论)得到“若q,则p”,即为逆命题;
(2)“换质”(即将原命题的条件与结论分别否定后作为条件和结论)得到“若??p,则??q”,即为否命题;
(3)既“换位”又“换质”(即把原命题的结论否定后作为新命题的条件,条件否定后作为新命题的结论)得到“若??q,则??p”,即为逆否命题.
3.要特别注意对一些常见形式的否定的写法,例如“都是”的否定为“不都是”,“a,b中至少一个为零”的否定为“a,b都不为零”.
4.在写命题的否定时,要注意对逻辑联结词的改变,即将“且”改写为“或”“或”改写为“且”.探究一探究二当堂检测变式训练1(1)命题:“若a2+b2=0(a,b∈R),则a=b=0”的逆否命题是( )
A.“若a≠b,b≠0(a,b∈R),则a2+b2≠0”
B.若a=b≠0(a,b∈R),则a2+b2≠0
C.若a≠0,且b≠0(a,b∈R),则a2+b2≠0
D.若a≠0或b≠0(a,b∈R),则a2+b2≠0
(2)命题“若x=3或y=5,则(x-3)(y-5)=0”的逆命题是 ;否命题是 ;逆否命题是 .?
解析(1)原命题的结论“a=b=0”实质是“a=0,且b=0”,所以它的否定是“a≠0或b≠0”,因此原命题的逆否命题是:若a≠0或b≠0(a,b∈R),则a2+b2≠0,选D.
答案(1)D (2)若(x-3)(y-5)=0,则x=3或y=5
若x≠3,且y≠5,则(x-3)(y-5)≠0 若(x-3)(y-5)≠0,则x≠3,且y≠5探究一探究二当堂检测 探究二四种命题的真假判断
例2 (1)对于原命题:“已知a、b、c∈R,若a>b,则ac2>bc2”,以及它的逆命题、否命题、逆否命题,在这4个命题中,真命题的个数为( )
A.0 B.1 C.2 D.4
(2)判断命题“若a≥0,则x2+x-a=0有实根”的逆否命题的真假.
思路分析(1)只需判断原命题和逆命题的真假即可.探究一探究二当堂检测(1)解析当c=0时,ac2>bc2不成立,故原命题是假命题,从而其逆否命题也是假命题;原命题的逆命题为“已知a、b、c∈R,若ac2>bc2,则a>b”是真命题,从而否命题也是真命题,故选C.
答案C
(2)解法一:原命题的逆否命题:若x2+x-a=0无实根,则a<0.
∵x2+x-a=0无实根,∴Δ=1+4a<0,解得a<- ,
∴原命题的逆否命题为真命题.
法二:∵a≥0,∴4a≥0,∴对于方程x2+x-a=0,根的判别式Δ=1+4a>0,∴方程x2+x-a=0有实根,故原命题为真命题.
∵原命题与其逆否命题等价,∴原命题的逆否命题为真命题.探究一探究二当堂检测延伸探究若将本例改为:判断命题“若a≥0,则x2+x-a>0恒成立”的真假.
解若x2+x-a>0恒成立,则Δ=1+4a<0,解得a<- .故原命题是假命题.
反思感悟判断命题真假的方法
(1)分清该命题的条件与结论,直接对该命题的真假进行判断;
(2)不直接写出命题,而是根据命题之间的关系进行判断,即原命题与其逆否命题等价、逆命题与否命题等价,特别是当命题本身不容易判断真假时,通常都通过判断其逆否命题的真假来实现.探究一探究二当堂检测变式训练2(1)命题“当AB=AC时,△ABC为等腰三角形”与它的逆命题、否命题、逆否命题中真命题的个数是( )
A.4 B.3 C.2 D.0
(2)有下列四个命题:①“若x+y=0,则x,y互为相反数”的否命题;②“若x>y,则x20”的否命题;④“等边三角形有两边相等”的逆命题.其中真命题的个数是( )
A.0 B.1 C.2 D.3探究一探究二当堂检测解析(1)当AB=AC时,△ABC为等腰三角形为真命题,故逆否命题为真命题.逆命题是△ABC为等腰三角形,则AB=AC为假命题,故否命题为假命题.
(2)①是真命题.其逆命题为“若x,y互为相反数,则x+y=0”,是真命题,因为原命题的否命题与其逆命题有相同的真假性,所以其否命题是真命题.②是假命题.原命题(如取x=1,y=0)是假命题,所以其逆否命题是假命题.③是假命题.该命题的否命题为“若x>3,则x2-x-6≤0”,显然是假命题.④是假命题.该命题的逆命题是“有两边相等的三角形是等边三角形”,显然是假命题.
答案(1)C (2)B探究一探究二当堂检测思想方法
等价性命题的应用
典例求证:当a2+b2=c2时,a,b,c不可能都是奇数.
思路分析可将要证明的问题看作一个命题,只需证明这个命题是真命题即可,若证明这个命题本身比较困难,则可以利用命题的等价性证明其逆否命题为真命题.
证明构造命题p:若a2+b2=c2,则a,b,c不可能都是奇数.
该命题的逆否命题是:若a,b,c都是奇数,则a2+b2≠c2.下面证明该逆否命题是真命题.
由于a,b,c都是奇数,则a2,b2,c2都是奇数,于是a2+b2必为偶数,而c2为奇数,所以有a2+b2≠c2,故逆否命题为真命题,从而原命题也是真命题.探究一探究二当堂检测反思感悟正难则反思想:在直接证明某一个命题为真命题有困难时,可以通过证明它的逆否命题为真命题,来间接地证明原命题为真命题.探究一探究二当堂检测跟踪训练求证:若a+b≥6,则a,b中至少有一个不小于3.
证明构造命题p:若a+b≥6,则a,b中至少有一个不小于3,则其逆否命题为:若a,b都小于3,则a+b<6.
而当a<3,且b<3时,必有a+b<6,所以逆否命题为真,从而原命题p为真命题,故原结论成立.探究一探究二当堂检测1.命题“若a>b,则a2>b2”的逆否命题是( )
A.若a2>b2,则a>b B.若a≤b,则a2≤b2
C.若a2≤b2,则a≤b D.若a>b,则a2≤b2
解析命题“若a>b,则a2>b2”,它的逆否命题是“若a2≤b2,则a≤b”.
答案C
2.在命题“若a=5,则a2=25”与其逆命题、否命题、逆否命题这四个命题中,假命题是( )
A.原命题、否命题 B.原命题、逆命题
C.原命题、逆否命题 D.逆命题、否命题
解析因为原命题为真,逆命题为假,所以逆否命题为真,否命题为假.
答案D探究一探究二当堂检测3.下列命题中,正确的个数是( )
①“若x,y都是奇数,则x+y是偶数”的否命题;②“全等三角形是相似三角形”的逆命题;③“圆内接四边形对角互补”的逆否命题.
A.3 B.2 C.1 D.0
答案C
4.命题“若α=β,则sin α=sin β”的等价命题是 .?
解析原命题与逆否命题是等价命题,所以命题“若α=β,则sin α=sin β”的等价命题是“若sin α≠sin β,则α≠β”.
答案若sin α≠sin β,则α≠β探究一探究二当堂检测5.已知命题p:“若ac≥0,则二次不等式ax2+bx+c>0无解”.
(1)写出命题p的否命题;
(2)判断命题p的否命题的真假.
解(1)命题p的否命题为:“若ac<0,则二次不等式ax2+bx+c>0有解”.
(2)命题p的否命题是真命题.
判断如下:
因为ac<0,
所以-ac>0,Δ=b2-4ac>0,所以二次方程ax2+bx+c=0有实根,即ax2+bx+c>0有解,所以该命题是真命题.
答案在两个命题中,如果第一个命题的条件是第二个命题的结论,且第一个命题的结论是第二个命题的条件,那么这两个命题叫做互为逆命题,其中一个叫做原命题,另一个叫做原命题的逆命题.1.四种命题
(1)逆命题
对于两个命题,如果一个命题的条件和结论分别为另一个命题的结论和条件,那么我们把这样的两个命题叫做互逆命题,其中一个叫做原命题,另一个叫做原命题的逆命题.如果原命题为“若p,则q”,则其逆命题为“若q,则p”.
(2)否命题
对于两个命题,如果一个命题的条件和结论分别为另一个命题的条件的否定和结论的否定,那么我们把这样的两个命题叫做互否命题,其中一个叫做原命题,另一个叫做原命题的否命题.如果原命题为“若p,则q”,那么其否命题为“若??p,则??q”.
(3)逆否命题
对于两个命题,如果一个命题的条件和结论分别为另一个命题的结论的否定和条件的否定,那么我们把这样的两个命题叫做互为逆否命题,其中一个叫做原命题,另一个叫做原命题的逆否命题.如果原命题为“若p,则q”,那么其逆否命题为“若??q,则??p”.名师点拨1.四种命题中的任何一个都可以作为原命题,即命题的四种形式中,原命题是不确定的.
2.“互为逆否命题”与“逆否命题”是不同的,互为逆否命题指的是两个命题之间的关系,具有双向性,而逆否命题指的是一个命题,具有单向性.【做一做1】 已知命题p:若x=y,则cos x=cos y,则命题p的逆命题为 ;命题p的否命题为 ;命题p的逆否命题为 .?
答案若cos x=cos y,则x=y 若x≠y,则cos x≠cos y 若cos x≠cos y,则x≠y2.四种命题间的关系 名师点拨四种命题之间共有互逆、互否、互为逆否三种关系:(1)互逆关系:原命题与逆命题;否命题与逆否命题;(2)互否关系:原命题与否命题;逆命题与逆否命题;(3)互为逆否关系(等价关系):原命题与逆否命题;逆命题与否命题.【做一做2】 给出以下命题:
①若一个四边形的四条边不相等,则它不是正方形;②若一个四边形对角互补,则它内接于圆;③正方形的四条边相等;④圆内接四边形对角互补;⑤对角不互补的四边形不内接于圆;⑥若一个四边形的边相等,则它是正方形.
其中互为逆命题的有 ;互为否命题的有 ;互为逆否命题的有 .?
解析命题③可改写为“若一个四边形是正方形,则它的四条边相等”;命题④可改写为“若一个四边形是圆内接四边形,则它的对角互补”;命题⑤可改写为“若一个四边形的对角不互补,则它不内接于圆”.因此互为逆命题的有③和⑥,②和④;互为否命题的有①和⑥,②和⑤;互为逆否命题的有①和③,④和⑤.
答案③和⑥,②和④ ①和⑥,②和⑤ ①和③,④和⑤3.四种命题的真假性关系
(1)四种命题的真假性,有以下四种情况:(2)四种命题的真假性之间的关系:
①两个命题互为逆否命题,它们的真假性相同;
②两个命题互为逆命题或互为否命题,它们的真假性没有关系.【做一做3】 命题“若a>-3,则a>-6”以及它的逆命题、否命题、逆否命题中,真命题的个数为( )
A.1 B.2
C.3 D.4
解析由a>-3可得a>-6,但由a>-6得不出a>-3,故原命题及原命题的逆否命题为真命题.
答案B探究一探究二当堂检测 探究一命题的四种形式
例1 写出下列各个命题的逆命题、否命题以及逆否命题.
(1)若sin α= ,则tan α= ;
(2)等底等高的两个三角形是全等三角形;
(3)当1
否命题:若两个三角形不等底或不等高,则这两个三角形不全等.
逆否命题:若两个三角形不全等,则这两个三角形不等底或不等高.
(3)逆命题:若x2-3x+2<0,则1
逆否命题:若x2-3x+2≥0,则x≤1或x≥2.
(4)逆命题:若a=0或b=0,则ab=0.
否命题:若ab≠0,则a≠0,且b≠0.
逆否命题:若a≠0,且b≠0,则ab≠0.探究一探究二当堂检测反思感悟四种命题的写法及注意事项
1.给出一个命题,写出其命题的四种形式时,首先要弄清楚该命题的条件和结论,若给出的命题不是“若p,则q”的形式,则应改写为“若p,则q”的形式,找出命题的条件和结论.
2.由原命题“若p,则q”写其他三种命题的方法:
(1)“换位”(即交换命题的条件与结论)得到“若q,则p”,即为逆命题;
(2)“换质”(即将原命题的条件与结论分别否定后作为条件和结论)得到“若??p,则??q”,即为否命题;
(3)既“换位”又“换质”(即把原命题的结论否定后作为新命题的条件,条件否定后作为新命题的结论)得到“若??q,则??p”,即为逆否命题.
3.要特别注意对一些常见形式的否定的写法,例如“都是”的否定为“不都是”,“a,b中至少一个为零”的否定为“a,b都不为零”.
4.在写命题的否定时,要注意对逻辑联结词的改变,即将“且”改写为“或”“或”改写为“且”.探究一探究二当堂检测变式训练1(1)命题:“若a2+b2=0(a,b∈R),则a=b=0”的逆否命题是( )
A.“若a≠b,b≠0(a,b∈R),则a2+b2≠0”
B.若a=b≠0(a,b∈R),则a2+b2≠0
C.若a≠0,且b≠0(a,b∈R),则a2+b2≠0
D.若a≠0或b≠0(a,b∈R),则a2+b2≠0
(2)命题“若x=3或y=5,则(x-3)(y-5)=0”的逆命题是 ;否命题是 ;逆否命题是 .?
解析(1)原命题的结论“a=b=0”实质是“a=0,且b=0”,所以它的否定是“a≠0或b≠0”,因此原命题的逆否命题是:若a≠0或b≠0(a,b∈R),则a2+b2≠0,选D.
答案(1)D (2)若(x-3)(y-5)=0,则x=3或y=5
若x≠3,且y≠5,则(x-3)(y-5)≠0 若(x-3)(y-5)≠0,则x≠3,且y≠5探究一探究二当堂检测 探究二四种命题的真假判断
例2 (1)对于原命题:“已知a、b、c∈R,若a>b,则ac2>bc2”,以及它的逆命题、否命题、逆否命题,在这4个命题中,真命题的个数为( )
A.0 B.1 C.2 D.4
(2)判断命题“若a≥0,则x2+x-a=0有实根”的逆否命题的真假.
思路分析(1)只需判断原命题和逆命题的真假即可.探究一探究二当堂检测(1)解析当c=0时,ac2>bc2不成立,故原命题是假命题,从而其逆否命题也是假命题;原命题的逆命题为“已知a、b、c∈R,若ac2>bc2,则a>b”是真命题,从而否命题也是真命题,故选C.
答案C
(2)解法一:原命题的逆否命题:若x2+x-a=0无实根,则a<0.
∵x2+x-a=0无实根,∴Δ=1+4a<0,解得a<- ,
∴原命题的逆否命题为真命题.
法二:∵a≥0,∴4a≥0,∴对于方程x2+x-a=0,根的判别式Δ=1+4a>0,∴方程x2+x-a=0有实根,故原命题为真命题.
∵原命题与其逆否命题等价,∴原命题的逆否命题为真命题.探究一探究二当堂检测延伸探究若将本例改为:判断命题“若a≥0,则x2+x-a>0恒成立”的真假.
解若x2+x-a>0恒成立,则Δ=1+4a<0,解得a<- .故原命题是假命题.
反思感悟判断命题真假的方法
(1)分清该命题的条件与结论,直接对该命题的真假进行判断;
(2)不直接写出命题,而是根据命题之间的关系进行判断,即原命题与其逆否命题等价、逆命题与否命题等价,特别是当命题本身不容易判断真假时,通常都通过判断其逆否命题的真假来实现.探究一探究二当堂检测变式训练2(1)命题“当AB=AC时,△ABC为等腰三角形”与它的逆命题、否命题、逆否命题中真命题的个数是( )
A.4 B.3 C.2 D.0
(2)有下列四个命题:①“若x+y=0,则x,y互为相反数”的否命题;②“若x>y,则x2
A.0 B.1 C.2 D.3探究一探究二当堂检测解析(1)当AB=AC时,△ABC为等腰三角形为真命题,故逆否命题为真命题.逆命题是△ABC为等腰三角形,则AB=AC为假命题,故否命题为假命题.
(2)①是真命题.其逆命题为“若x,y互为相反数,则x+y=0”,是真命题,因为原命题的否命题与其逆命题有相同的真假性,所以其否命题是真命题.②是假命题.原命题(如取x=1,y=0)是假命题,所以其逆否命题是假命题.③是假命题.该命题的否命题为“若x>3,则x2-x-6≤0”,显然是假命题.④是假命题.该命题的逆命题是“有两边相等的三角形是等边三角形”,显然是假命题.
答案(1)C (2)B探究一探究二当堂检测思想方法
等价性命题的应用
典例求证:当a2+b2=c2时,a,b,c不可能都是奇数.
思路分析可将要证明的问题看作一个命题,只需证明这个命题是真命题即可,若证明这个命题本身比较困难,则可以利用命题的等价性证明其逆否命题为真命题.
证明构造命题p:若a2+b2=c2,则a,b,c不可能都是奇数.
该命题的逆否命题是:若a,b,c都是奇数,则a2+b2≠c2.下面证明该逆否命题是真命题.
由于a,b,c都是奇数,则a2,b2,c2都是奇数,于是a2+b2必为偶数,而c2为奇数,所以有a2+b2≠c2,故逆否命题为真命题,从而原命题也是真命题.探究一探究二当堂检测反思感悟正难则反思想:在直接证明某一个命题为真命题有困难时,可以通过证明它的逆否命题为真命题,来间接地证明原命题为真命题.探究一探究二当堂检测跟踪训练求证:若a+b≥6,则a,b中至少有一个不小于3.
证明构造命题p:若a+b≥6,则a,b中至少有一个不小于3,则其逆否命题为:若a,b都小于3,则a+b<6.
而当a<3,且b<3时,必有a+b<6,所以逆否命题为真,从而原命题p为真命题,故原结论成立.探究一探究二当堂检测1.命题“若a>b,则a2>b2”的逆否命题是( )
A.若a2>b2,则a>b B.若a≤b,则a2≤b2
C.若a2≤b2,则a≤b D.若a>b,则a2≤b2
解析命题“若a>b,则a2>b2”,它的逆否命题是“若a2≤b2,则a≤b”.
答案C
2.在命题“若a=5,则a2=25”与其逆命题、否命题、逆否命题这四个命题中,假命题是( )
A.原命题、否命题 B.原命题、逆命题
C.原命题、逆否命题 D.逆命题、否命题
解析因为原命题为真,逆命题为假,所以逆否命题为真,否命题为假.
答案D探究一探究二当堂检测3.下列命题中,正确的个数是( )
①“若x,y都是奇数,则x+y是偶数”的否命题;②“全等三角形是相似三角形”的逆命题;③“圆内接四边形对角互补”的逆否命题.
A.3 B.2 C.1 D.0
答案C
4.命题“若α=β,则sin α=sin β”的等价命题是 .?
解析原命题与逆否命题是等价命题,所以命题“若α=β,则sin α=sin β”的等价命题是“若sin α≠sin β,则α≠β”.
答案若sin α≠sin β,则α≠β探究一探究二当堂检测5.已知命题p:“若ac≥0,则二次不等式ax2+bx+c>0无解”.
(1)写出命题p的否命题;
(2)判断命题p的否命题的真假.
解(1)命题p的否命题为:“若ac<0,则二次不等式ax2+bx+c>0有解”.
(2)命题p的否命题是真命题.
判断如下:
因为ac<0,
所以-ac>0,Δ=b2-4ac>0,所以二次方程ax2+bx+c=0有实根,即ax2+bx+c>0有解,所以该命题是真命题.
