高中数学新人教A版选修2-1课件:第一章常用逻辑用语1.3简单的逻辑联结词(27张)
文档属性
| 名称 | 高中数学新人教A版选修2-1课件:第一章常用逻辑用语1.3简单的逻辑联结词(27张) |

|
|
| 格式 | zip | ||
| 文件大小 | 348.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-20 00:00:00 | ||
图片预览








文档简介
课件27张PPT。1.3 简单的逻辑联结词【思考】观察三个命题:①2是4的约数;②2是6的约数;③2是8的约数且是10的约数,它们之间有什么关系?从集合的角度如何理解“且”的含义.
答案命题③是将命题①,②用“且”联结得到的新命题,“且”与集合运算中交集的定义A∩B={x|x∈A且x∈B}中“且”的意义相同,表示“并且”,“同时”的意思.“且”作为逻辑联结词,与生活用语中“既……,又……”相同,表示两者都要满足的意思,在日常生活中经常用“和”“与”代替.1.逻辑联结词“且”“或”“非”
(1)用逻辑联结词“且”把命题p和命题q联结起来,就得到一个新命题,记作p∧q,读作“p且q”.
(2)用逻辑联结词“或”把命题p和命题q联结起来,就得到一个新命题,记作p∨q,读作“p或q”.
(3)对一个命题p全盘否定,就得到一个新命题,记作??p,读作“非p”或“p的否定”.
名师点拨1.对于逻辑联结词“且”“或”“非”,可以分别结合集合中的“交集”“并集”“补集”来进行理解.
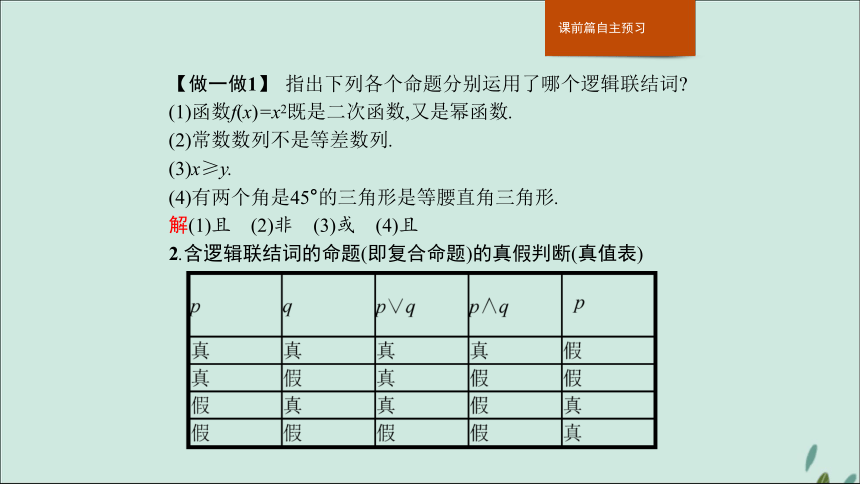
2.一个命题的否定与命题的否命题不同,命题的否定只是将命题的结论进行否定,而否命题则是将命题的条件和结论都进行否定.【做一做1】 指出下列各个命题分别运用了哪个逻辑联结词?
(1)函数f(x)=x2既是二次函数,又是幂函数.
(2)常数数列不是等差数列.
(3)x≥y.
(4)有两个角是45°的三角形是等腰直角三角形.
解(1)且 (2)非 (3)或 (4)且
2.含逻辑联结词的命题(即复合命题)的真假判断(真值表)名师点拨注意以上真值表的逆用,当p∧q为真时,p和q都必须是真命题;当p∨q为真时,p和q中至少有一个是真命题;当p∨q为假时,p和q都必须是假命题;当p∧q为假时,p和q中至少有一个是假命题.【做一做2】 已知命题:
p:对任意x∈R,总有2x>0;
q:“x>1”是“x>2”的充分不必要条件.
则下列命题为真命题的是( )
A.p∧q B.(??p)∧(??q)
C.(??p)∧q D.p∧(??q)
解析因为指数函数的值域为(0,+∞),所以对任意x∈R,y=2x>0恒成立,故p为真命题;因为当x>1时,x>2不一定成立,反之当x>2时,一定有x>1成立,故“x>1”是“x>2”的必要不充分条件,故q为假命题,则p∧q、??p为假命题,??q为真命题,(??p)∧(??q)、(??p)∧q为假命题,p∧(??q)为真命题,故选D.
答案D探究一探究二探究三当堂检测 探究一含逻辑联结词的命题的构成
例1 指出下列命题的构成形式,以及构成它的简单命题:
(1)1是质数或合数;
(2)他是运动员兼教练;
(3)不等式|x-2|≤0没有实数解;
(4)要么周长相等的两个三角形全等,要么面积相等的两个三角形全等;
(5)这部作品不仅艺术上有缺点,而且政治上也有错误.探究一探究二探究三当堂检测思路分析根据命题中所使用的逻辑联结词,或者命题所表达的实际意义判断命题的结构.
解(1)这个命题是p∨q形式,其中p:1是质数,q:1是合数.
(2)这个命题是p∧q形式,其中p:他是运动员,q:他是教练.
(3)这个命题是??p形式,其中p:不等式|x-2|≤0有实数解.
(4)这个命题是p∨q形式,其中p:周长相等的两个三角形全等,q:面积相等的两个三角形全等.
(5)这个命题是p∧q形式,其中p:这部作品艺术上有缺点,q:这部作品政治上有错误.探究一探究二探究三当堂检测反思感悟复合命题的判断及注意的问题
1.辨别含逻辑联结词的命题的构成形式时,应根据组成含逻辑联结词的命题的语句中所出现的逻辑联结词,或语句的意义确定含逻辑联结词的命题的形式,准确理解语义应注意抓住一些关键词.如“是……也是……”,“兼”,“不但……而且……”,“既……又……”,“要么……,要么……”等.
2.要注意数学中和生活中一些特殊表达方式和特殊关系式.如a≥3是a>3或a=3,xy=0是x=0或y=0,x2+y2=0是x=0且y=0.
3.如果要用逻辑联结词“且”“或”“非”联结两个命题,关键是正确理解这些词语的意义及在日常生活中的同义词,选择合适的联结词,有时为了语法的要求及语句的通顺也可进行适当的省略和变形.
4.常见词语及其否定形式:是→不是,相等→不相等,>→≤,<→≥,都是→不都是,都不是→至少有一个是.探究一探究二探究三当堂检测变式训练1指出下列命题的构成形式,以及构成它的简单命题:
(1)48是16与12的公倍数;
(2)方程x2+x+3=0没有实数根;
(3)相似三角形的周长相等或对应角相等;
(4)垂直于弦的直径平分这条弦,并且平分弦所对的两段弧.
解(1)这个命题是p∧q形式,其中p:48是16的倍数,q:48是12的倍数.
(2)这个命题是??p形式,其中p:方程x2+x+3=0有实数根.
(3)这个命题是p∨q形式,其中p:相似三角形周长相等,q:相似三角形对应角相等.
(4)这个命题是p∧q形式,其中p:垂直于弦的直径平分这条弦,q:垂直于弦的直径平分这条弦所对的两段弧.探究一探究二探究三当堂检测探究二含逻辑联结词的命题的真假判断
例2 分别指出由下列简单命题所构成的“p∧q”“p∨q”“??p”形式的命题的真假.
(1)p:2是奇数,q:2是合数;
(2)p:函数f(x)=3x-3-x是偶函数,q:函数f(x)=3x-3-x是单调递增函数;
(3)p:点(1,2)在直线2x+y-4=0上,q:点(1,2)不在圆x2+(y-3)2=2上;
(4)p:不等式x2-x+2<0没有实数解,q:函数y=x2-x+2的图象与x轴没有交点.探究一探究二探究三当堂检测思路分析分析判断出每个简单命题的真假,然后结合真值表得到每个复合命题的真假.
解(1)因为p是假命题,q是假命题,
所以p∧q是假命题,p∨q是假命题,??p是真命题.
(2)因为p是假命题,q是真命题,
所以p∧q是假命题,p∨q是真命题,??p是真命题.
(3)因为p是真命题,q是假命题,
所以p∧q是假命题,p∨q是真命题,??p是假命题.
(4)因为p是真命题,q是真命题,
所以p∧q是真命题,p∨q是真命题,??p是假命题.探究一探究二探究三当堂检测反思感悟判断“p∧q”“p∨q”“??p”形式的命题真假的步骤
第一步,确定复合命题的构成形式;
第二步,判断简单命题p,q的真假;
第三步,根据真值表作出判断.
其中特别要注意:一真“或”为真,一假“且”即假.探究一探究二探究三当堂检测变式训练2(1)已知命题p:方程x2-2ax-1=0有两个实数根;命题q:函数f(x)=x+ 的最小值为4.给出下列命题:
①p∧q;②p∨q;③p∧(??q);④(??p)∨(??q).
则其中真命题的个数为( )
A.1 B.2 C.3 D.4
(2)已知命题p:对任意x∈R,总有2x>0,q:“x>1”是“x>2”的充分不必要条件,则下列命题为真命题的是( )
A.p∧q B.(??p)∧(??q)
C.(??p)∧q D.p∧(??q)探究一探究二探究三当堂检测解析(1)由于Δ=(-2a)2-4×1×(-1)=4a2+4>0,所以方程x2-2ax-1=0有两个实数根,所以命题p是真命题;当x<0时,f(x)=x+ <0,所以命题q为假命题,所以p∨q,p∧(??q),(??p)∨(??q)是真命题,故选C.
(2)由题意知,p是真命题,q是假命题,所以p∧(??q)是真命题.
答案(1)C (2)D探究一探究二探究三当堂检测探究三命题的否定及其应用
例3 (1)写出下列命题的否定形式:
①函数f(x)=sin 3x是周期函数;
②面积相等的三角形都是全等三角形;
③若m2+n2+p2=0,则m,n,p全为0.
(2)若p:x2-2x-3>0,q: >0,试判断??p是??q的什么条件?思路分析(1)按照命题否定的定义进行改写,注意常见词语的否定形式,如果是“若p则q”的形式,则只否定其结论;(2)两种思路,一是直接将??p,??q的范围写出来,通过集合间的包含关系进行判断,二是判断p与q的关系,利用等价关系得到??p是??q的什么条件.探究一探究二探究三当堂检测解(1)各个命题的否定形式分别是:
①函数f(x)=sin 3x不是周期函数.
②面积相等的三角形不都是全等三角形.
③若m2+n2+p2=0,则m,n,p不全为0.
(2)(方法1)因为x2-2x-3>0?x>3或x<-1,所以??p:-1≤x≤3.
又因为 >0?x2-x-6>0?x>3或x<-2,
所以??q:-2≤x≤3.
因为{x|-1≤x≤3}?{x|-2≤x≤3},所以??p是??q的充分不必要条件.
(方法2)因为p:x2-2x-3>0?x>3或x<-1,q: >0?x2-x-6>0?x>3或x<-2,
所以p是q的必要不充分条件,故??p是??q的充分不必要条件.探究一探究二探究三当堂检测反思感悟1.注意区分命题的否定与命题的否命题,二者是有区别的,对于“若p,则q”形式的命题,其否命题是“若??p,则??q”,即条件和结论都进行否定,而命题的否定只对全称命题和特称命题进行否定.
2.若p是q的充分不必要条件,即p?q,q p,则由原命题与其逆否命题的等价性可知,??q???p,??p ??q,所以??p是??q的必要不充分条件;同理,若p是q的必要不充分条件,则??p是??q的充分不必要条件;若p是q的充要条件,则??p是??q的充要条件.因此在判断??p与??q之间的关系时,可以借助下表进行恰当的转化,简化解题过程.探究一探究二探究三当堂检测规范解答
一题多变——由复合命题的真假求参数的取值范围
典例已知命题p:关于x的方程x2+mx+1=0有两个不相等的负根,命题q:关于x的方程4x2+4(m-2)x+1=0无实根.若p∨q为真命题,p∧q为假命题,求m的取值范围.探究一探究二探究三当堂检测延伸探究1本例题条件不变,试求p∧q为真命题时m的取值范围.
解由例题知,当p为真时,m>2,当q为真时,11(a>0,且a≠1)的解集是{x|x<0}”,命题q改为“函数y=lg(ax2-x+a)的定义域为R”.其他不变,试求a的取值范围.
解根据关于x的不等式ax>1(a>0,且a≠1)的解集为{x|x<0},知00的解集为探究一探究二探究三当堂检测方法总结根据命题的真假求参数范围的步骤
(1)求出命题p、q均为真时参数的取值范围;
(2)根据命题p∧q、p∨q的真假判断命题p、q的真假;
(3)根据命题p、q的真假求出参数的取值范围.探究一探究二探究三当堂检测1.下列命题中是“p∧q”形式的命题是( )
A.28是5的倍数或是7的倍数
B.2是方程x2-4=0的根又是方程x-2=0的根
C.函数y=ax(a>1)是增函数
D.函数y=ln x是减函数
答案B
2.已知命题p:2+2=5,命题q:3>2,则下列判断正确的是( )
A.“p∨q”为假,“??q”为假
B.“p∨q”为真,“??q”为假
C.“p∧q”为假,“??p”为假
D.“p∧q”为真,“p∨q”为假
解析显然p假q真,故“p∨q”为真,“p∧q”为假,“??p”为真,“??q”为假,故选B.
答案B探究一探究二探究三当堂检测A.p∧q B.(??p)∧(??q)
C.(??p)∧q D.p∧(??q)答案C 探究一探究二探究三当堂检测4.已知命题p:函数f(x)=log0.5(3-x)定义域为(-∞,3);命题q:若k<0,则函数h(x)= 在(0,+∞)上是减函数.则下列结论中错误的是 .(填序号)?
①命题“p∧q”为真;②命题“p∨(??q)”为假;③命题“p∨q”为假;④命题“(??p)∧(??q)”为假.
解析由3-x>0,得x<3,所以命题p为真,所以命题??p为假.又由k<0,易知函数h(x)= 在(0,+∞)上是增函数,所以命题q为假,所以命题??q为真.所以命题“p∧q”为假,命题“p∨(??q)”为真,命题“p∨q”为真,命题“(??p)∧(??q)”为假,故答案为①②③.
答案①②③探究一探究二探究三当堂检测5.设有两个命题:①关于x的不等式mx2+1>0的解集是R;②函数f(x)=logmx是减函数.如果这两个命题中有且只有一个真命题,那么实数m的取值范围是 .?
解析①是真命题,则m≥0,②是真命题,则0答案{0}∪[1,+∞)
答案命题③是将命题①,②用“且”联结得到的新命题,“且”与集合运算中交集的定义A∩B={x|x∈A且x∈B}中“且”的意义相同,表示“并且”,“同时”的意思.“且”作为逻辑联结词,与生活用语中“既……,又……”相同,表示两者都要满足的意思,在日常生活中经常用“和”“与”代替.1.逻辑联结词“且”“或”“非”
(1)用逻辑联结词“且”把命题p和命题q联结起来,就得到一个新命题,记作p∧q,读作“p且q”.
(2)用逻辑联结词“或”把命题p和命题q联结起来,就得到一个新命题,记作p∨q,读作“p或q”.
(3)对一个命题p全盘否定,就得到一个新命题,记作??p,读作“非p”或“p的否定”.
名师点拨1.对于逻辑联结词“且”“或”“非”,可以分别结合集合中的“交集”“并集”“补集”来进行理解.
2.一个命题的否定与命题的否命题不同,命题的否定只是将命题的结论进行否定,而否命题则是将命题的条件和结论都进行否定.【做一做1】 指出下列各个命题分别运用了哪个逻辑联结词?
(1)函数f(x)=x2既是二次函数,又是幂函数.
(2)常数数列不是等差数列.
(3)x≥y.
(4)有两个角是45°的三角形是等腰直角三角形.
解(1)且 (2)非 (3)或 (4)且
2.含逻辑联结词的命题(即复合命题)的真假判断(真值表)名师点拨注意以上真值表的逆用,当p∧q为真时,p和q都必须是真命题;当p∨q为真时,p和q中至少有一个是真命题;当p∨q为假时,p和q都必须是假命题;当p∧q为假时,p和q中至少有一个是假命题.【做一做2】 已知命题:
p:对任意x∈R,总有2x>0;
q:“x>1”是“x>2”的充分不必要条件.
则下列命题为真命题的是( )
A.p∧q B.(??p)∧(??q)
C.(??p)∧q D.p∧(??q)
解析因为指数函数的值域为(0,+∞),所以对任意x∈R,y=2x>0恒成立,故p为真命题;因为当x>1时,x>2不一定成立,反之当x>2时,一定有x>1成立,故“x>1”是“x>2”的必要不充分条件,故q为假命题,则p∧q、??p为假命题,??q为真命题,(??p)∧(??q)、(??p)∧q为假命题,p∧(??q)为真命题,故选D.
答案D探究一探究二探究三当堂检测 探究一含逻辑联结词的命题的构成
例1 指出下列命题的构成形式,以及构成它的简单命题:
(1)1是质数或合数;
(2)他是运动员兼教练;
(3)不等式|x-2|≤0没有实数解;
(4)要么周长相等的两个三角形全等,要么面积相等的两个三角形全等;
(5)这部作品不仅艺术上有缺点,而且政治上也有错误.探究一探究二探究三当堂检测思路分析根据命题中所使用的逻辑联结词,或者命题所表达的实际意义判断命题的结构.
解(1)这个命题是p∨q形式,其中p:1是质数,q:1是合数.
(2)这个命题是p∧q形式,其中p:他是运动员,q:他是教练.
(3)这个命题是??p形式,其中p:不等式|x-2|≤0有实数解.
(4)这个命题是p∨q形式,其中p:周长相等的两个三角形全等,q:面积相等的两个三角形全等.
(5)这个命题是p∧q形式,其中p:这部作品艺术上有缺点,q:这部作品政治上有错误.探究一探究二探究三当堂检测反思感悟复合命题的判断及注意的问题
1.辨别含逻辑联结词的命题的构成形式时,应根据组成含逻辑联结词的命题的语句中所出现的逻辑联结词,或语句的意义确定含逻辑联结词的命题的形式,准确理解语义应注意抓住一些关键词.如“是……也是……”,“兼”,“不但……而且……”,“既……又……”,“要么……,要么……”等.
2.要注意数学中和生活中一些特殊表达方式和特殊关系式.如a≥3是a>3或a=3,xy=0是x=0或y=0,x2+y2=0是x=0且y=0.
3.如果要用逻辑联结词“且”“或”“非”联结两个命题,关键是正确理解这些词语的意义及在日常生活中的同义词,选择合适的联结词,有时为了语法的要求及语句的通顺也可进行适当的省略和变形.
4.常见词语及其否定形式:是→不是,相等→不相等,>→≤,<→≥,都是→不都是,都不是→至少有一个是.探究一探究二探究三当堂检测变式训练1指出下列命题的构成形式,以及构成它的简单命题:
(1)48是16与12的公倍数;
(2)方程x2+x+3=0没有实数根;
(3)相似三角形的周长相等或对应角相等;
(4)垂直于弦的直径平分这条弦,并且平分弦所对的两段弧.
解(1)这个命题是p∧q形式,其中p:48是16的倍数,q:48是12的倍数.
(2)这个命题是??p形式,其中p:方程x2+x+3=0有实数根.
(3)这个命题是p∨q形式,其中p:相似三角形周长相等,q:相似三角形对应角相等.
(4)这个命题是p∧q形式,其中p:垂直于弦的直径平分这条弦,q:垂直于弦的直径平分这条弦所对的两段弧.探究一探究二探究三当堂检测探究二含逻辑联结词的命题的真假判断
例2 分别指出由下列简单命题所构成的“p∧q”“p∨q”“??p”形式的命题的真假.
(1)p:2是奇数,q:2是合数;
(2)p:函数f(x)=3x-3-x是偶函数,q:函数f(x)=3x-3-x是单调递增函数;
(3)p:点(1,2)在直线2x+y-4=0上,q:点(1,2)不在圆x2+(y-3)2=2上;
(4)p:不等式x2-x+2<0没有实数解,q:函数y=x2-x+2的图象与x轴没有交点.探究一探究二探究三当堂检测思路分析分析判断出每个简单命题的真假,然后结合真值表得到每个复合命题的真假.
解(1)因为p是假命题,q是假命题,
所以p∧q是假命题,p∨q是假命题,??p是真命题.
(2)因为p是假命题,q是真命题,
所以p∧q是假命题,p∨q是真命题,??p是真命题.
(3)因为p是真命题,q是假命题,
所以p∧q是假命题,p∨q是真命题,??p是假命题.
(4)因为p是真命题,q是真命题,
所以p∧q是真命题,p∨q是真命题,??p是假命题.探究一探究二探究三当堂检测反思感悟判断“p∧q”“p∨q”“??p”形式的命题真假的步骤
第一步,确定复合命题的构成形式;
第二步,判断简单命题p,q的真假;
第三步,根据真值表作出判断.
其中特别要注意:一真“或”为真,一假“且”即假.探究一探究二探究三当堂检测变式训练2(1)已知命题p:方程x2-2ax-1=0有两个实数根;命题q:函数f(x)=x+ 的最小值为4.给出下列命题:
①p∧q;②p∨q;③p∧(??q);④(??p)∨(??q).
则其中真命题的个数为( )
A.1 B.2 C.3 D.4
(2)已知命题p:对任意x∈R,总有2x>0,q:“x>1”是“x>2”的充分不必要条件,则下列命题为真命题的是( )
A.p∧q B.(??p)∧(??q)
C.(??p)∧q D.p∧(??q)探究一探究二探究三当堂检测解析(1)由于Δ=(-2a)2-4×1×(-1)=4a2+4>0,所以方程x2-2ax-1=0有两个实数根,所以命题p是真命题;当x<0时,f(x)=x+ <0,所以命题q为假命题,所以p∨q,p∧(??q),(??p)∨(??q)是真命题,故选C.
(2)由题意知,p是真命题,q是假命题,所以p∧(??q)是真命题.
答案(1)C (2)D探究一探究二探究三当堂检测探究三命题的否定及其应用
例3 (1)写出下列命题的否定形式:
①函数f(x)=sin 3x是周期函数;
②面积相等的三角形都是全等三角形;
③若m2+n2+p2=0,则m,n,p全为0.
(2)若p:x2-2x-3>0,q: >0,试判断??p是??q的什么条件?思路分析(1)按照命题否定的定义进行改写,注意常见词语的否定形式,如果是“若p则q”的形式,则只否定其结论;(2)两种思路,一是直接将??p,??q的范围写出来,通过集合间的包含关系进行判断,二是判断p与q的关系,利用等价关系得到??p是??q的什么条件.探究一探究二探究三当堂检测解(1)各个命题的否定形式分别是:
①函数f(x)=sin 3x不是周期函数.
②面积相等的三角形不都是全等三角形.
③若m2+n2+p2=0,则m,n,p不全为0.
(2)(方法1)因为x2-2x-3>0?x>3或x<-1,所以??p:-1≤x≤3.
又因为 >0?x2-x-6>0?x>3或x<-2,
所以??q:-2≤x≤3.
因为{x|-1≤x≤3}?{x|-2≤x≤3},所以??p是??q的充分不必要条件.
(方法2)因为p:x2-2x-3>0?x>3或x<-1,q: >0?x2-x-6>0?x>3或x<-2,
所以p是q的必要不充分条件,故??p是??q的充分不必要条件.探究一探究二探究三当堂检测反思感悟1.注意区分命题的否定与命题的否命题,二者是有区别的,对于“若p,则q”形式的命题,其否命题是“若??p,则??q”,即条件和结论都进行否定,而命题的否定只对全称命题和特称命题进行否定.
2.若p是q的充分不必要条件,即p?q,q p,则由原命题与其逆否命题的等价性可知,??q???p,??p ??q,所以??p是??q的必要不充分条件;同理,若p是q的必要不充分条件,则??p是??q的充分不必要条件;若p是q的充要条件,则??p是??q的充要条件.因此在判断??p与??q之间的关系时,可以借助下表进行恰当的转化,简化解题过程.探究一探究二探究三当堂检测规范解答
一题多变——由复合命题的真假求参数的取值范围
典例已知命题p:关于x的方程x2+mx+1=0有两个不相等的负根,命题q:关于x的方程4x2+4(m-2)x+1=0无实根.若p∨q为真命题,p∧q为假命题,求m的取值范围.探究一探究二探究三当堂检测延伸探究1本例题条件不变,试求p∧q为真命题时m的取值范围.
解由例题知,当p为真时,m>2,当q为真时,1
解根据关于x的不等式ax>1(a>0,且a≠1)的解集为{x|x<0},知0
(1)求出命题p、q均为真时参数的取值范围;
(2)根据命题p∧q、p∨q的真假判断命题p、q的真假;
(3)根据命题p、q的真假求出参数的取值范围.探究一探究二探究三当堂检测1.下列命题中是“p∧q”形式的命题是( )
A.28是5的倍数或是7的倍数
B.2是方程x2-4=0的根又是方程x-2=0的根
C.函数y=ax(a>1)是增函数
D.函数y=ln x是减函数
答案B
2.已知命题p:2+2=5,命题q:3>2,则下列判断正确的是( )
A.“p∨q”为假,“??q”为假
B.“p∨q”为真,“??q”为假
C.“p∧q”为假,“??p”为假
D.“p∧q”为真,“p∨q”为假
解析显然p假q真,故“p∨q”为真,“p∧q”为假,“??p”为真,“??q”为假,故选B.
答案B探究一探究二探究三当堂检测A.p∧q B.(??p)∧(??q)
C.(??p)∧q D.p∧(??q)答案C 探究一探究二探究三当堂检测4.已知命题p:函数f(x)=log0.5(3-x)定义域为(-∞,3);命题q:若k<0,则函数h(x)= 在(0,+∞)上是减函数.则下列结论中错误的是 .(填序号)?
①命题“p∧q”为真;②命题“p∨(??q)”为假;③命题“p∨q”为假;④命题“(??p)∧(??q)”为假.
解析由3-x>0,得x<3,所以命题p为真,所以命题??p为假.又由k<0,易知函数h(x)= 在(0,+∞)上是增函数,所以命题q为假,所以命题??q为真.所以命题“p∧q”为假,命题“p∨(??q)”为真,命题“p∨q”为真,命题“(??p)∧(??q)”为假,故答案为①②③.
答案①②③探究一探究二探究三当堂检测5.设有两个命题:①关于x的不等式mx2+1>0的解集是R;②函数f(x)=logmx是减函数.如果这两个命题中有且只有一个真命题,那么实数m的取值范围是 .?
解析①是真命题,则m≥0,②是真命题,则0
