高中数学新人教A版选修2-1课件:模块复习课第1课时常用逻辑用语(30张)
文档属性
| 名称 | 高中数学新人教A版选修2-1课件:模块复习课第1课时常用逻辑用语(30张) |  | |
| 格式 | zip | ||
| 文件大小 | 620.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-20 21:45:52 | ||
图片预览









文档简介
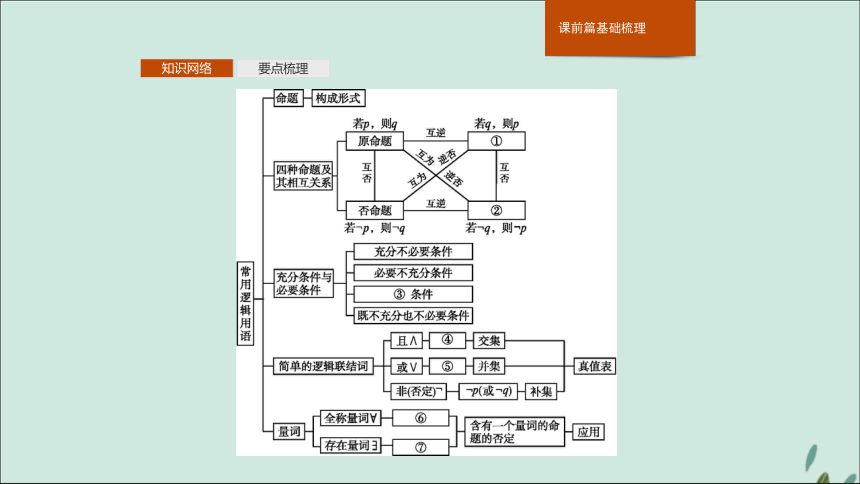
课件30张PPT。模块复习课第1课时 常用逻辑用语知识网络要点梳理知识网络要点梳理填一填:① ;② ;③ ;④ ;⑤ ;⑥ ;⑦ .?
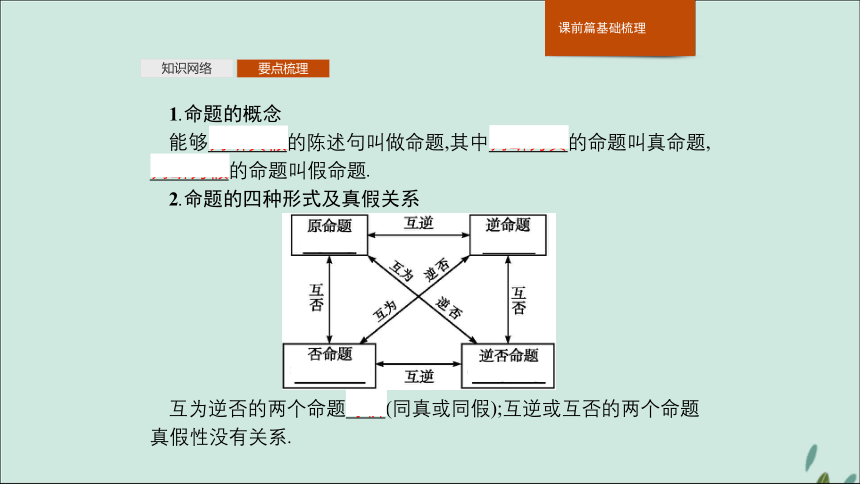
答案①逆命题 ②逆否命题 ③充分必要 ④p∧q ⑤p∨q ⑥全称命题 ⑦特称命题知识网络要点梳理1.命题的概念
能够判断真假的陈述句叫做命题,其中判断为真的命题叫真命题,判断为假的命题叫假命题.
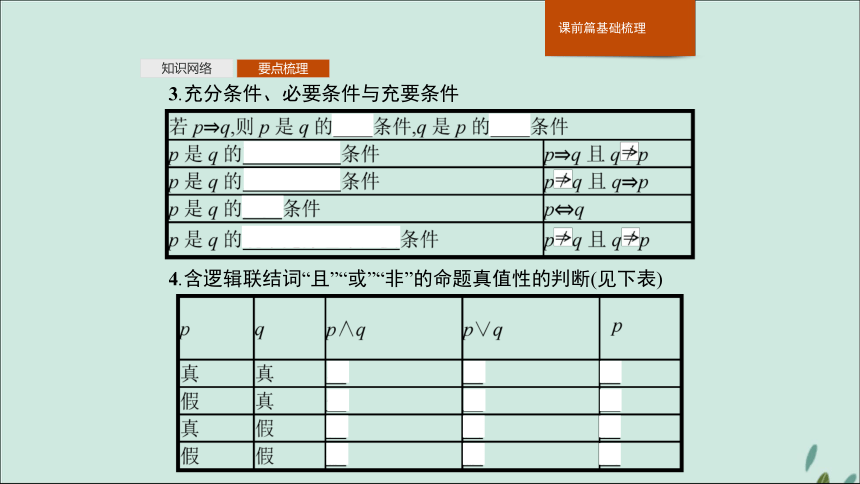
2.命题的四种形式及真假关系互为逆否的两个命题等价(同真或同假);互逆或互否的两个命题真假性没有关系.知识网络要点梳理3.充分条件、必要条件与充要条件 4.含逻辑联结词“且”“或”“非”的命题真值性的判断(见下表) 知识网络要点梳理5.全称量词与全称命题
(1)全称量词:短语“所有的”在陈述中表示所述事物的全体,逻辑中通常叫做全称量词,并用符号“?”表示.
(2)全称命题:含有全称量词的命题.
(3)全称命题的符号表示:形如“对M中的所有x,p(x)”的命题,用符号简记为“?x∈M,p(x)”.知识网络要点梳理6.存在量词与存在性命题
(1)存在量词:短语“存在一个”或“有些”或“至少有一个”在陈述中表示所述事物的个体或部分,逻辑中通常叫做存在量词,并用符号“?”表示.
(2)存在性命题:含有存在量词的命题.
(3)存在性命题的符号表示:形如“存在集合M中的元素x,q(x)”的命题,用符号简记为?x∈M,q(x).
(4)全称命题与存在性命题的否定专题归纳高考体验专题一 四种命题及其真假判定
例1 已知下面四个命题:
①对于?x,若x-3=0,则x-3≤0;
②命题“设a,b是非零向量且a·b=0,则a⊥b”的逆命题;
③“m>n>0”是“方程mx2+ny2=1表示焦点在y轴上的椭圆”的充分而不必要条件;
④已知p,q为两个命题,若“p∨q”为假命题,则“(??p)∧(??q)”为真命题.
其中所有真命题的序号是 .?
思路分析对于②③要注意四种命题及其关系,对于④涉及含逻辑联结词的命题,要根据真值表与逻辑联结词的含义判断.专题归纳高考体验自主解答①∵x-3=0?x-3≤0,∴为真命题.
②逆命题:“若a⊥b,则a·b=0”为真命题.
此椭圆焦点在y轴上,反之亦成立.
所以“m>n>0”是“方程mx2+ny2=1表示焦点在y轴上的椭圆”的充要条件.∴题目结论为假命题.
④由p∨q为假命题,∴p与q均为假命题.
∴??p,??q为真命题,一定有(??p)∧(??q)为真,故④为真命题.
综上知,命题①②④为真命题.
答案①②④反思感悟四种命题真假的判断方法
因为互为逆否命题的真假等价,所以判断四个命题的真假,只需判断原命题与逆命题(或否命题)的真假即可.专题归纳高考体验跟踪训练1写出下列命题的逆命题、否命题和逆否命题,并判断它们的真假:
(1)相等的两个角的正弦值相等;
(2)若x2-2x-3=0,则x=3.
解(1)逆命题:若两个角的正弦值相等,则这两个角相等,假命题;
否命题:若两个角不相等,则这两个角的正弦值也不相等,假命题;
逆否命题:若两个角的正弦值不相等,则这两个角不相等,真命题.
(2)逆命题:若x=3,则x2-2x-3=0,真命题;
否命题:若x2-2x-3≠0,则x≠3,真命题;
逆否命题:若x≠3,则x2-2x-3≠0,假命题.专题归纳高考体验专题二 充分条件、必要条件的判断及应用
例2 下列各小题中,p是q的充要条件的是( )
①p:m<-2或m>6;q:y=x2+mx+m+3有两个不同的零点;
②p: =1;q:y=f(x)为偶函数;
③p:cos α=cos β;q:tan α=tan β;
④p:A∩B=A;q:?UB??UA.
A.①② B.②③
C.③④ D.①④
思路分析把握充要条件的概念,会用反例来排除选项.专题归纳高考体验自主解答对于①,∵y=x2+mx+m+3有两个不同零点,∴m2-4(m+3)>0,解得m<-2或m>6.∴p是q的充要条件,排除选项B,C.
对于②,q:取f(x)=x2,其在R上为偶函数,但 在x=0处没有意义,p是q的充分不必要条件,排除选项A.
答案D反思感悟充分条件与必要条件的判断方法
(1)直接利用定义判断:即若p?q成立,则p是q的充分条件,q是p的必要条件.(条件与结论是相对的)
(2)利用等价命题的关系判断:p?q的等价命题是??q???p,即若??q???p成立,则p是q的充分条件,q是p的必要条件.专题归纳高考体验跟踪训练2已知p:x2-(a+1)x+a≤0,q:1≤x≤3,若p是q的必要不充分条件,则实数a的取值范围是 .?
解析x2-(a+1)x+a≤0,即(x-1)(x-a)≤0,
p是q的必要不充分条件,
当a=1时,由(x-1)(x-1)≤0得x=1,此时不满足条件,
当a<1时,由(x-1)(x-a)≤0得a≤x≤1,此时不满足条件,
当a>1时,由(x-1)(x-a)≤0得1≤x≤a,
若p是q的必要不充分条件,则a>3,
即实数a的取值范围是(3,+∞).
答案(3,+∞)专题归纳高考体验专题三 全称命题与特称命题
例3 判断下列命题是特称命题还是全称命题,用符号写出其否定并判断命题的否定的真假.
(1)有一个实数α,使得sin2α+cos2α≠1;
(2)任何一条直线都存在斜率;
(3)存在实数x,使得 =2.
思路分析首先找准量词判断是全称命题还是特称命题,写它们的否定时要注意量词的变化,真假判断可从原命题和原命题的否定两个角度择易处理.答案(1)特称命题,否定:?α∈R,sin2α+cos2α=1,真命题.
(2)全称命题,否定:?直线l,l没有斜率,真命题.
(3)特称命题,否定:?x∈R, ≠2,真命题.专题归纳高考体验反思感悟1.全称命题与特称命题真假的判断方法
(1)判断全称命题为真命题,需严格的逻辑推理证明,判断全称命题为假命题,只需举出反例.
(2)判断特称命题为真命题,需要举出正例,而判断特称命题为假命题时,要有严格的逻辑证明.
2.含有一个量词的命题否定的关注点
全称命题的否定是特称命题,特称命题的否定是全称命题,否定时既要改写量词,又要否定结论.专题归纳高考体验跟踪训练3下列命题为假命题是( )
A.?x0∈R,lg x0=0
B.?x0∈R,tan x0=1
C.?x∈R,x3>3
D.?x∈R,2x>0
解析∵当x=1时,lg 1=0,∴A是真命题.
∵当x= 时,tan =1,∴B是真命题.
∵当x<0时,x3<0,∴C是假命题.
由指数函数的性质可知,对?x∈R,2x>0成立,∴D是真命题.
答案C专题归纳高考体验专题四 转化与化归思想
例4 已知命题p:f(x)=x2+2(m-1)x+3在区间(-∞,0)上是减函数;
命题q:不等式x2-4x+1-m≤0无解.
若命题“p∨q”为真,命题“p∧q”为假,求实数m的取值范围.
思路分析如果命题p∨q为真,命题p∧q为假,则命题p,q一真一假,进而可得实数m的取值范围.专题归纳高考体验解f(x)=x2+2(m-1)x+3的图象是开口朝上,且以直线x=1-m为对称轴的抛物线,
若命题p:f(x)=x2+2(m-1)x+3在区间(-∞,0)上是减函数为真命题,
则1-m≥0,即m≤1;
命题q:“不等式x2-4x+1-m≤0无解”,
则Δ=16-4(1-m)<0,即m<-3.
如果命题p∨q为真,命题p∧q为假,则命题p,q一真一假,
若p真,q假,则-3≤m≤1,
若p假,q真,则不存在满足条件的m值,
∴-3≤m≤1.
∴实数m的取值范围是[-3,1].专题归纳高考体验反思感悟转化与化归思想的应用
所谓转化与化归思想是指在研究和解决问题时,采用某种手段将问题通过变换、转化,进而使问题得到解决的一种解题策略.一般是将复杂的问题进行变换,转化为简单的问题,将较难的问题通过变换,转化为容易求解的问题,将未解决的问题转化为已解决的问题.专题归纳高考体验跟踪训练4已知命题r(x):?x∈R,sin x+cos x>m成立;s(x):?x∈R,x2+mx+1>0成立.若r(x)为假命题,s(x)为真命题,求实数m的取值范围.又对任意的x∈R,s(x)为真命题,即对任意的x∈R,不等式x2+mx+1>0成立,所以Δ=m2-4<0,即-2故如果对任意的x∈R,r(x)为假命题且s(x)为真命题,应有
- ≤m<2.
故实数m的取值范围是[- ,2).专题归纳高考体验考点一 含有一个量词的命题的否定
1.(2015课标全国Ⅰ高考)设命题p:?n∈N,n2>2n,则??p为( )
A.?n∈N,n2>2n
B.?n∈N,n2≤2n
C.?n∈N,n2≤2n
D.?n∈N,n2=2n
解析∵p:?n∈N,n2>2n,∴??p:?n∈N,n2≤2n.故选C.
答案C专题归纳高考体验考点二 四种命题及相互关系 答案C 专题归纳高考体验考点三 充分、必要条件的判定
3.(2019天津高考)设x∈R,则“x2-5x<0”是“|x-1|<1”的( )
A.充分而不必要条件
B.必要而不充分条件
C.充要条件
D.既不充分也不必要条件
解析由x2-5x<0,得0答案B专题归纳高考体验A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件答案C 专题归纳高考体验考点四 命题真假的判断
5.(2017课标Ⅰ高考)设有下面四个命题
p1:若复数z满足 ∈R,则z∈R;
p2:若复数z满足z2∈R,则z∈R;
p3:若复数z1,z2满足z1z2∈R,则z1= ;
p4:若复数z∈R,则 ∈R.
其中的真命题为( )
A.p1,p3 B.p1,p4 C.p2,p3 D.p2,p4p2:因为i2=-1∈R,而z=i?R,故p2不正确;
p3:若z1=1,z2=2,则z1z2=2,满足z1z2∈R,而它们实部不相等,不是共轭复数,故p3不正确;
p4:实数的虚部为0,它的共轭复数是它本身,也属于实数,故p4正确.
答案B专题归纳高考体验6.(2017山东高考)已知命题p:?x>0,ln(x+1)>0;命题q:若a>b,则a2>b2,下列命题为真命题的是( )
A.p∧q B.p∧??q
C.??p∧q D.??p∧??q
解析对?x>0,都有x+1>1,所以ln(x+1)>0,故p为真命题.又1>-2,但12<(-2)2,故q为假命题,所以??q为真命题,故p∧??q为真命题.故选B.
答案B专题归纳高考体验7.(2014湖南高考)已知命题p:若x>y,则-x<-y;命题q:若x>y,则x2>y2.在命题①p∧q;②p∨q;③p∧(??q);④(??p)∨q中,真命题是( )
A.①③ B.①④
C.②③ D.②④
解析由题易知命题p为真,命题q为假,则??p为假,??q为真.故p∧q为假,p∨q为真,p∧(??q)为真,(??p)∨q为假.故选C.
答案C专题归纳高考体验8.(2014课标全国Ⅰ高考)不等式组 的解集记为D,有下面四个命题:
p1:?(x,y)∈D,x+2y≥-2,
p2:?(x,y)∈D,x+2y≥2,
p3:?(x,y)∈D,x+2y≤3,
p4:?(x,y)∈D,x+2y≤-1,
其中的真命题是( )
A.p2,p3 B.p1,p2
C.p1,p4 D.p1,p3专题归纳高考体验解析画出可行域如图阴影部分所示.
作直线l0:y=- x,平移l0,当直线经过A(2,-1)时,x+2y取最小值,此时(x+2y)min=0.故p1:?(x,y)∈D,x+2y≥-2为真.p2:?(x,y)∈D,x+2y≥2为真.故选B.
答案B
答案①逆命题 ②逆否命题 ③充分必要 ④p∧q ⑤p∨q ⑥全称命题 ⑦特称命题知识网络要点梳理1.命题的概念
能够判断真假的陈述句叫做命题,其中判断为真的命题叫真命题,判断为假的命题叫假命题.
2.命题的四种形式及真假关系互为逆否的两个命题等价(同真或同假);互逆或互否的两个命题真假性没有关系.知识网络要点梳理3.充分条件、必要条件与充要条件 4.含逻辑联结词“且”“或”“非”的命题真值性的判断(见下表) 知识网络要点梳理5.全称量词与全称命题
(1)全称量词:短语“所有的”在陈述中表示所述事物的全体,逻辑中通常叫做全称量词,并用符号“?”表示.
(2)全称命题:含有全称量词的命题.
(3)全称命题的符号表示:形如“对M中的所有x,p(x)”的命题,用符号简记为“?x∈M,p(x)”.知识网络要点梳理6.存在量词与存在性命题
(1)存在量词:短语“存在一个”或“有些”或“至少有一个”在陈述中表示所述事物的个体或部分,逻辑中通常叫做存在量词,并用符号“?”表示.
(2)存在性命题:含有存在量词的命题.
(3)存在性命题的符号表示:形如“存在集合M中的元素x,q(x)”的命题,用符号简记为?x∈M,q(x).
(4)全称命题与存在性命题的否定专题归纳高考体验专题一 四种命题及其真假判定
例1 已知下面四个命题:
①对于?x,若x-3=0,则x-3≤0;
②命题“设a,b是非零向量且a·b=0,则a⊥b”的逆命题;
③“m>n>0”是“方程mx2+ny2=1表示焦点在y轴上的椭圆”的充分而不必要条件;
④已知p,q为两个命题,若“p∨q”为假命题,则“(??p)∧(??q)”为真命题.
其中所有真命题的序号是 .?
思路分析对于②③要注意四种命题及其关系,对于④涉及含逻辑联结词的命题,要根据真值表与逻辑联结词的含义判断.专题归纳高考体验自主解答①∵x-3=0?x-3≤0,∴为真命题.
②逆命题:“若a⊥b,则a·b=0”为真命题.
此椭圆焦点在y轴上,反之亦成立.
所以“m>n>0”是“方程mx2+ny2=1表示焦点在y轴上的椭圆”的充要条件.∴题目结论为假命题.
④由p∨q为假命题,∴p与q均为假命题.
∴??p,??q为真命题,一定有(??p)∧(??q)为真,故④为真命题.
综上知,命题①②④为真命题.
答案①②④反思感悟四种命题真假的判断方法
因为互为逆否命题的真假等价,所以判断四个命题的真假,只需判断原命题与逆命题(或否命题)的真假即可.专题归纳高考体验跟踪训练1写出下列命题的逆命题、否命题和逆否命题,并判断它们的真假:
(1)相等的两个角的正弦值相等;
(2)若x2-2x-3=0,则x=3.
解(1)逆命题:若两个角的正弦值相等,则这两个角相等,假命题;
否命题:若两个角不相等,则这两个角的正弦值也不相等,假命题;
逆否命题:若两个角的正弦值不相等,则这两个角不相等,真命题.
(2)逆命题:若x=3,则x2-2x-3=0,真命题;
否命题:若x2-2x-3≠0,则x≠3,真命题;
逆否命题:若x≠3,则x2-2x-3≠0,假命题.专题归纳高考体验专题二 充分条件、必要条件的判断及应用
例2 下列各小题中,p是q的充要条件的是( )
①p:m<-2或m>6;q:y=x2+mx+m+3有两个不同的零点;
②p: =1;q:y=f(x)为偶函数;
③p:cos α=cos β;q:tan α=tan β;
④p:A∩B=A;q:?UB??UA.
A.①② B.②③
C.③④ D.①④
思路分析把握充要条件的概念,会用反例来排除选项.专题归纳高考体验自主解答对于①,∵y=x2+mx+m+3有两个不同零点,∴m2-4(m+3)>0,解得m<-2或m>6.∴p是q的充要条件,排除选项B,C.
对于②,q:取f(x)=x2,其在R上为偶函数,但 在x=0处没有意义,p是q的充分不必要条件,排除选项A.
答案D反思感悟充分条件与必要条件的判断方法
(1)直接利用定义判断:即若p?q成立,则p是q的充分条件,q是p的必要条件.(条件与结论是相对的)
(2)利用等价命题的关系判断:p?q的等价命题是??q???p,即若??q???p成立,则p是q的充分条件,q是p的必要条件.专题归纳高考体验跟踪训练2已知p:x2-(a+1)x+a≤0,q:1≤x≤3,若p是q的必要不充分条件,则实数a的取值范围是 .?
解析x2-(a+1)x+a≤0,即(x-1)(x-a)≤0,
p是q的必要不充分条件,
当a=1时,由(x-1)(x-1)≤0得x=1,此时不满足条件,
当a<1时,由(x-1)(x-a)≤0得a≤x≤1,此时不满足条件,
当a>1时,由(x-1)(x-a)≤0得1≤x≤a,
若p是q的必要不充分条件,则a>3,
即实数a的取值范围是(3,+∞).
答案(3,+∞)专题归纳高考体验专题三 全称命题与特称命题
例3 判断下列命题是特称命题还是全称命题,用符号写出其否定并判断命题的否定的真假.
(1)有一个实数α,使得sin2α+cos2α≠1;
(2)任何一条直线都存在斜率;
(3)存在实数x,使得 =2.
思路分析首先找准量词判断是全称命题还是特称命题,写它们的否定时要注意量词的变化,真假判断可从原命题和原命题的否定两个角度择易处理.答案(1)特称命题,否定:?α∈R,sin2α+cos2α=1,真命题.
(2)全称命题,否定:?直线l,l没有斜率,真命题.
(3)特称命题,否定:?x∈R, ≠2,真命题.专题归纳高考体验反思感悟1.全称命题与特称命题真假的判断方法
(1)判断全称命题为真命题,需严格的逻辑推理证明,判断全称命题为假命题,只需举出反例.
(2)判断特称命题为真命题,需要举出正例,而判断特称命题为假命题时,要有严格的逻辑证明.
2.含有一个量词的命题否定的关注点
全称命题的否定是特称命题,特称命题的否定是全称命题,否定时既要改写量词,又要否定结论.专题归纳高考体验跟踪训练3下列命题为假命题是( )
A.?x0∈R,lg x0=0
B.?x0∈R,tan x0=1
C.?x∈R,x3>3
D.?x∈R,2x>0
解析∵当x=1时,lg 1=0,∴A是真命题.
∵当x= 时,tan =1,∴B是真命题.
∵当x<0时,x3<0,∴C是假命题.
由指数函数的性质可知,对?x∈R,2x>0成立,∴D是真命题.
答案C专题归纳高考体验专题四 转化与化归思想
例4 已知命题p:f(x)=x2+2(m-1)x+3在区间(-∞,0)上是减函数;
命题q:不等式x2-4x+1-m≤0无解.
若命题“p∨q”为真,命题“p∧q”为假,求实数m的取值范围.
思路分析如果命题p∨q为真,命题p∧q为假,则命题p,q一真一假,进而可得实数m的取值范围.专题归纳高考体验解f(x)=x2+2(m-1)x+3的图象是开口朝上,且以直线x=1-m为对称轴的抛物线,
若命题p:f(x)=x2+2(m-1)x+3在区间(-∞,0)上是减函数为真命题,
则1-m≥0,即m≤1;
命题q:“不等式x2-4x+1-m≤0无解”,
则Δ=16-4(1-m)<0,即m<-3.
如果命题p∨q为真,命题p∧q为假,则命题p,q一真一假,
若p真,q假,则-3≤m≤1,
若p假,q真,则不存在满足条件的m值,
∴-3≤m≤1.
∴实数m的取值范围是[-3,1].专题归纳高考体验反思感悟转化与化归思想的应用
所谓转化与化归思想是指在研究和解决问题时,采用某种手段将问题通过变换、转化,进而使问题得到解决的一种解题策略.一般是将复杂的问题进行变换,转化为简单的问题,将较难的问题通过变换,转化为容易求解的问题,将未解决的问题转化为已解决的问题.专题归纳高考体验跟踪训练4已知命题r(x):?x∈R,sin x+cos x>m成立;s(x):?x∈R,x2+mx+1>0成立.若r(x)为假命题,s(x)为真命题,求实数m的取值范围.又对任意的x∈R,s(x)为真命题,即对任意的x∈R,不等式x2+mx+1>0成立,所以Δ=m2-4<0,即-2
- ≤m<2.
故实数m的取值范围是[- ,2).专题归纳高考体验考点一 含有一个量词的命题的否定
1.(2015课标全国Ⅰ高考)设命题p:?n∈N,n2>2n,则??p为( )
A.?n∈N,n2>2n
B.?n∈N,n2≤2n
C.?n∈N,n2≤2n
D.?n∈N,n2=2n
解析∵p:?n∈N,n2>2n,∴??p:?n∈N,n2≤2n.故选C.
答案C专题归纳高考体验考点二 四种命题及相互关系 答案C 专题归纳高考体验考点三 充分、必要条件的判定
3.(2019天津高考)设x∈R,则“x2-5x<0”是“|x-1|<1”的( )
A.充分而不必要条件
B.必要而不充分条件
C.充要条件
D.既不充分也不必要条件
解析由x2-5x<0,得0
C.充分必要条件 D.既不充分也不必要条件答案C 专题归纳高考体验考点四 命题真假的判断
5.(2017课标Ⅰ高考)设有下面四个命题
p1:若复数z满足 ∈R,则z∈R;
p2:若复数z满足z2∈R,则z∈R;
p3:若复数z1,z2满足z1z2∈R,则z1= ;
p4:若复数z∈R,则 ∈R.
其中的真命题为( )
A.p1,p3 B.p1,p4 C.p2,p3 D.p2,p4p2:因为i2=-1∈R,而z=i?R,故p2不正确;
p3:若z1=1,z2=2,则z1z2=2,满足z1z2∈R,而它们实部不相等,不是共轭复数,故p3不正确;
p4:实数的虚部为0,它的共轭复数是它本身,也属于实数,故p4正确.
答案B专题归纳高考体验6.(2017山东高考)已知命题p:?x>0,ln(x+1)>0;命题q:若a>b,则a2>b2,下列命题为真命题的是( )
A.p∧q B.p∧??q
C.??p∧q D.??p∧??q
解析对?x>0,都有x+1>1,所以ln(x+1)>0,故p为真命题.又1>-2,但12<(-2)2,故q为假命题,所以??q为真命题,故p∧??q为真命题.故选B.
答案B专题归纳高考体验7.(2014湖南高考)已知命题p:若x>y,则-x<-y;命题q:若x>y,则x2>y2.在命题①p∧q;②p∨q;③p∧(??q);④(??p)∨q中,真命题是( )
A.①③ B.①④
C.②③ D.②④
解析由题易知命题p为真,命题q为假,则??p为假,??q为真.故p∧q为假,p∨q为真,p∧(??q)为真,(??p)∨q为假.故选C.
答案C专题归纳高考体验8.(2014课标全国Ⅰ高考)不等式组 的解集记为D,有下面四个命题:
p1:?(x,y)∈D,x+2y≥-2,
p2:?(x,y)∈D,x+2y≥2,
p3:?(x,y)∈D,x+2y≤3,
p4:?(x,y)∈D,x+2y≤-1,
其中的真命题是( )
A.p2,p3 B.p1,p2
C.p1,p4 D.p1,p3专题归纳高考体验解析画出可行域如图阴影部分所示.
作直线l0:y=- x,平移l0,当直线经过A(2,-1)时,x+2y取最小值,此时(x+2y)min=0.故p1:?(x,y)∈D,x+2y≥-2为真.p2:?(x,y)∈D,x+2y≥2为真.故选B.
答案B
