高中数学新人教A版选修2-1课件:模块复习课第4课时利用向量解决平行与垂直、夹角问题(52张)
文档属性
| 名称 | 高中数学新人教A版选修2-1课件:模块复习课第4课时利用向量解决平行与垂直、夹角问题(52张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-20 21:48:52 | ||
图片预览








文档简介
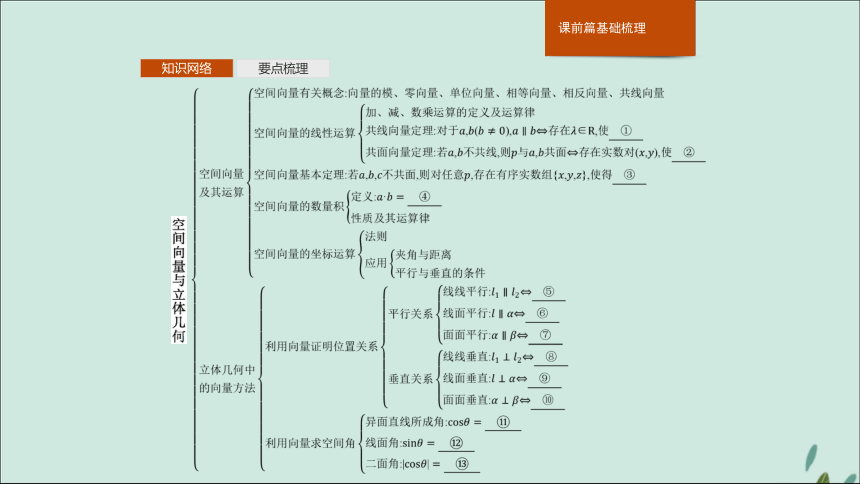
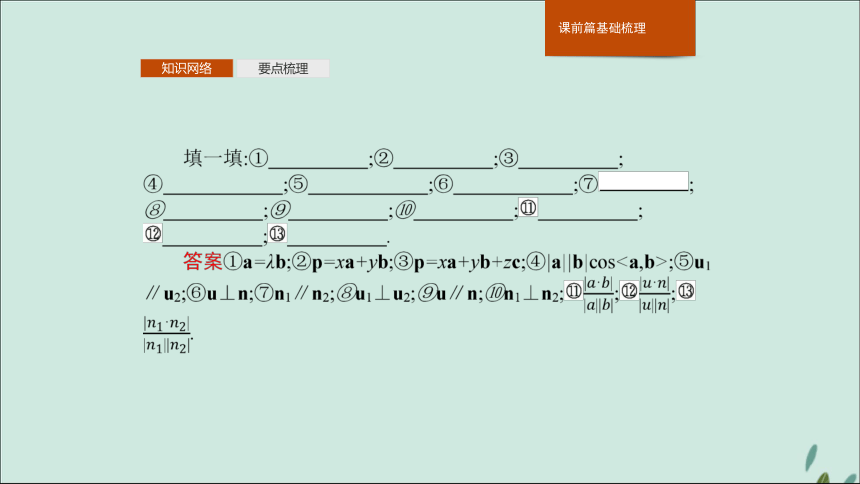
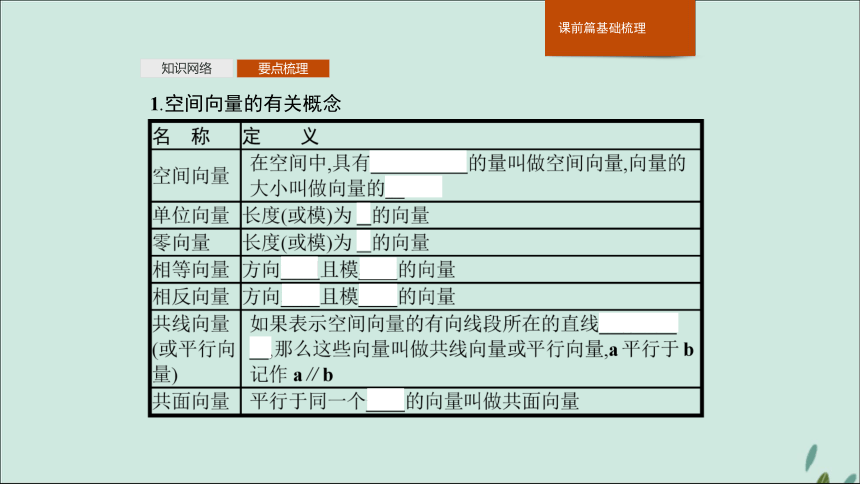
课件52张PPT。第4课时 利用向量解决平行与垂直、 夹角问题知识网络要点梳理知识网络要点梳理知识网络要点梳理1.空间向量的有关概念 知识网络要点梳理2.空间向量的线性运算及运算律 (2)运算律:a.加法交换律:a+b=b+a;
b.加法结合律:(a+b)+c=a+(b+c);
c.数乘分配律:λ(a+b)=λa+λb.知识网络要点梳理3.空间向量的有关定理知识网络要点梳理4.空间向量的数量积及运算律
(1)数量积及相关概念
①两向量的夹角②两向量的数量积
已知空间两个非零向量a,b,则|a|·|b|·cos叫做向量a,b的数量积,记作a·b,即a·b=|a||b|cos.
(2)空间向量数量积的运算律
①结合律:(λa)·b=λ(a·b);
②交换律:a·b=b·a;
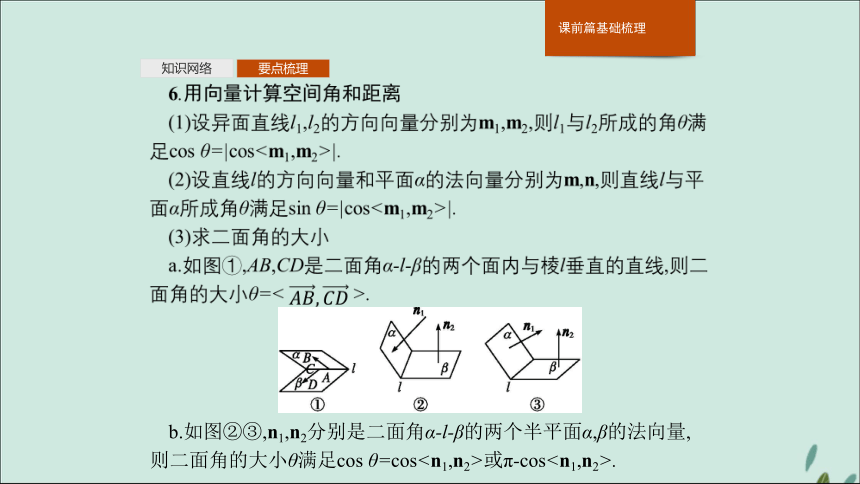
③分配律:a·(b+c)=a·b+a·c.知识网络要点梳理5.向量的坐标运算 知识网络要点梳理?b.如图②③,n1,n2分别是二面角α-l-β的两个半平面α,β的法向量,则二面角的大小θ满足cos θ=cos或π-cos.专题归纳高考体验专题一 空间向量概念及运算 (2)求向量a与向量b的夹角的余弦值;
(3)若ka+b与ka-2b互相垂直,求实数k的值.专题归纳高考体验(2)∵a=(1,1,0),b=(-1,0,2),
∴a·b=(1,1,0)·(-1,0,2)=-1. (3)法一:∵ka+b=(k-1,k,2),ka-2b=(k+2,k,-4),且ka+b与ka-2b互相垂直,∴(k-1,k,2)·(k+2,k,-4)=(k-1)(k+2)+k2-8=0.专题归纳高考体验反思感悟数量积的应用
(1)求夹角:设向量a,b所成的角为θ,则cos θ= ,进而可求两异面直线所成的角.
(2)求长度(距离):运用公式|a|2=a·a,可使线段长度的计算问题转化为向量数量积的计算问题.
(3)解决垂直问题:利用a⊥b?a·b=0(a≠0,b≠0),可将垂直问题转化为向量数量积的计算问题.专题归纳高考体验跟踪训练1已知空间向量a=(0,-1,1),b=(4,1,0).
(1)若(ka-b)⊥b,则k= .?
(2)若|λa+b|= ,且λ>0,则λ的值为 .?解析(1)因为(ka-b)⊥b,所以(ka-b)·b=0,
即ka·b-|b|2=0,
因此-k-17=0,解得k=-17.
(2)因为a=(0,-1,1),b=(4,1,0),
所以λa+b=λ(0,-1,1)+(4,1,0)=(4,1-λ,λ).
因为|λa+b|= ,所以42+(1-λ)2+λ2=29,
整理得λ2-λ-6=0,解得λ=3或λ=-2,
又因为λ>0,故λ=3.
答案(1)-17 (2)3专题归纳高考体验专题二 利用空间向量证明位置关系
例2 如图所示,在直三棱柱ABC-A1B1C1中,∠ABC=90°,BC=2,CC1=4,EB1=1,D,F,G分别为CC1,B1C1,A1C1的中点,EF与B1D相交于点H.
求证:(1)B1D⊥平面ABD;
(2)平面EGF∥平面ABD.
思路分析建立空间直角坐标系,通过坐标运算,结合线面垂直,面面平行的判定定理进行证明.专题归纳高考体验证明(1)如图所示,建立空间直角坐标系,设A1(a,0,0),
则B1(0,0,0),C1(0,2,0),F(0,1,0),E(0,0,1),A(a,0,4),B(0,0,4),D(0,2,2),G专题归纳高考体验反思感悟向量法证明空间中的位置关系 专题归纳高考体验跟踪训练2如图所示,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB于点F.
求证:(1)PA∥平面EDB;
(2)平面PBD⊥平面EFD.专题归纳高考体验证明以D点为坐标原点, 所在的方向为x,y,z轴建立空间直角坐标系D-xyz(如图所示).设DC=a.
(1)连接AC,交BD于G,连接EG.专题归纳高考体验由已知EF⊥PB,且EF∩DE=E,
所以PB⊥平面EFD.又因为PB?平面PBD,
所以平面PBD⊥平面EFD.专题归纳高考体验专题三 利用空间向量求空间角
例3 (2018全国Ⅰ高考)如图,四边形ABCD为正方形,E,F分别为AD,BC的中点,以DF为折痕把△DFC折起,使点C到达点P的位置,且PF⊥BF.
(1)证明:平面PEF⊥平面ABFD;
(2)求DP与平面ABFD所成角的正弦值.解(1)由已知可得,BF⊥PF,BF⊥EF,
所以BF⊥平面PEF.
又BF?平面ABFD,所以平面PEF⊥平面ABFD.专题归纳高考体验(2)作PH⊥EF,垂足为H.由(1)得,PH⊥平面ABFD.
以H为坐标原点, 的方向为y轴正方向,| |为单位长,建立如图所示的空间直角坐标系H-xyz.专题归纳高考体验反思感悟向量法求解空间角 专题归纳高考体验跟踪训练3如图,正方体ABCD-A1B1C1D1中,M是棱BB1的中点.
(1)求直线A1M与平面AMC1所成角的正弦值.
(2)求二面角A-MC1-A1的余弦值.专题归纳高考体验解以B为坐标原点,BC,BA,BB1所在的直线分别为x轴,y轴,z轴建立空间直角坐标系,专题归纳高考体验专题归纳高考体验考点一 空间向量及其运算
1.(2018全国Ⅱ高考)已知向量a,b满足|a|=1,a·b=-1,则a·(2a-b)=( )
A.4 B.3 C.2 D.0
解析a·(2a-b)=2a2-a·b=2-(-1)=3.
答案B专题归纳高考体验考点二 利用空间向量求空间角 A.30° B.45°
C.60° D.120° 答案A 专题归纳高考体验3.(2019全国Ⅰ高考)如图,直四棱柱ABCD-A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.
(1)证明:MN∥平面C1DE;
(2)求二面角A-MA1-N的正弦值.解(1)连接B1C,ME.
因为M,E分别为BB1,BC的中点,
所以ME∥B1C,且ME= B1C.
又因为N为A1D的中点,所以ND= A1D.
由题设知A1B1??DC,可得B1C??A1D,
故ME??ND,
因此四边形MNDE为平行四边形,MN∥ED.
又MN?平面EDC1,所以MN∥平面C1DE.专题归纳高考体验(2)由已知可得DE⊥DA.
以D为坐标原点, 的方向为x轴正方向,建立如图所示的空间直角坐标系D-xyz,专题归纳高考体验专题归纳高考体验4.(2017课标Ⅱ高考)如图,四棱锥P-ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC= AD,∠BAD=∠ABC=90°,E是PD的中点.
(1)证明:直线CE∥平面PAB;
(2)点M在棱PC上,且直线BM与底面ABCD所成角为45°,求二面角M-AB-D的余弦值.专题归纳高考体验解(1)取PA的中点F,连接EF,BF.
因为E是PD的中点,所以EF∥AD,EF= AD.
由∠BAD=∠ABC=90°得BC∥AD,
又BC= AD,所以EF??BC,四边形BCEF是平行四边形,CE∥BF,
又BF?平面PAB,CE?平面PAB,
故CE∥平面PAB.专题归纳高考体验因为BM与底面ABCD所成的角为45°,
而n=(0,0,1)是底面ABCD的法向量,专题归纳高考体验专题归纳高考体验5.(2019全国Ⅲ高考)图1是由矩形ADEB,Rt△ABC和菱形BFGC组成的一个平面图形,其中AB=1,BE=BF=2,∠FBC=60°.将其沿AB,BC折起使得BE与BF重合,连结DG,如图2.(1)证明:图2中的A,C,G,D四点共面,且平面ABC⊥平面BCGE;
(2)求图2中的二面角B-CG-A的大小. 专题归纳高考体验(1)证明由已知得AD∥BE,CG∥BE,所以AD∥CG,
故AD,CG确定一个平面,从而A,C,G,D四点共面.
由已知得AB⊥BE,AB⊥BC,故AB⊥平面BCGE.
又因为AB?平面ABC,
所以平面ABC⊥平面BCGE.
(2)解作EH⊥BC,垂足为H.
因为EH?平面BCGE,平面BCGE⊥平面ABC,所以EH⊥平面ABC.
由已知,菱形BCGE的边长为2,∠EBC=60°,可求得以H为坐标原点, 的方向为x轴的正方向,建立如图所示的空间直角坐标系H-xyz,专题归纳高考体验专题归纳高考体验6.(2018全国Ⅱ高考)如图,在三棱锥P-ABC中,AB=BC=2 ,PA=PB=PC=AC=4,O为AC的中点.
(1)证明:PO⊥平面ABC;
(2)若点M在棱BC上,且二面角M-PA-C为30°,求PC与平面PAM所成角的正弦值.专题归纳高考体验解(1)因为AP=CP=AC=4,O为AC的中点,所以OP⊥AC,且 由OP2+OB2=PB2知PO⊥OB.
由OP⊥OB,OP⊥AC知PO⊥平面ABC.
(2)如图,以O为坐标原点, 的方向为x轴正方向,建立空间直角坐标系O-xyz.专题归纳高考体验专题归纳高考体验专题归纳高考体验7.(2018北京高考)如图,在三棱柱ABC-A1B1C1中,CC1⊥平面ABC,D,E,F,G分别为AA1,AC,A1C1,BB1的中点,AB=BC= ,AC=AA1=2.
(1)求证:AC⊥平面BEF;
(2)求二面角B-CD-C1的余弦值;
(3)证明:直线FG与平面BCD相交.(1)证明在三棱柱ABC-A1B1C1中,
∵CC1⊥平面ABC,
∴四边形A1ACC1为矩形.
又E,F分别为AC,A1C1的中点,
∴AC⊥EF.∵AB=BC,
∴AC⊥BE,∴AC⊥平面BEF.专题归纳高考体验(2)解由(1)知AC⊥EF,AC⊥BE,EF∥CC1.
∵CC1⊥平面ABC,∴EF⊥平面ABC.
∵BE?平面ABC,∴EF⊥BE.
建立如图所示的空间直角坐标系E-xyz.专题归纳高考体验专题归纳高考体验考点三 利用空间向量解决综合问题
8.(2018天津高考)如图,AD∥BC且AD=2BC,AD⊥CD,EG∥AD且EG=AD,CD∥FG且CD=2FG,DG⊥平面ABCD,DA=DC=DG=2.
(1)若M为CF的中点,N为EG的中点,求证:MN∥平面CDE;
(2)求二面角E-BC-F的正弦值;
(3)若点P在线段DG上,且直线BP与平面ADGE所成的角为60°,求线段DP的长.专题归纳高考体验专题归纳高考体验专题归纳高考体验专题归纳高考体验9.(2019北京高考)如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD⊥CD,AD∥BC,PA=AD=CD=2,BC=3.E为PD的中点,点F在PC上,且 .
(1)求证:CD⊥平面PAD;
(2)求二面角F-AE-P的余弦值;
(3)设点G在PB上,且 ,判断直线AG是否在平面AEF内,说明理由.专题归纳高考体验(1)证明因为PA⊥平面ABCD,所以PA⊥CD.
又因为AD⊥CD,所以CD⊥平面PAD.
(2)解过A作AD的垂线交BC于点M.
因为PA⊥平面ABCD,
所以PA⊥AM,PA⊥AD.
如图建立空间直角坐标系A-xyz,则A(0,0,0),B(2,-1,0),C(2,2,0),D(0,2,0),P(0,0,2).
因为E为PD的中点,所以E(0,1,1).专题归纳高考体验令z=1,则y=-1,x=-1.
于是n=(-1,-1,1).
又因为平面PAD的法向量为p=(1,0,0),专题归纳高考体验
b.加法结合律:(a+b)+c=a+(b+c);
c.数乘分配律:λ(a+b)=λa+λb.知识网络要点梳理3.空间向量的有关定理知识网络要点梳理4.空间向量的数量积及运算律
(1)数量积及相关概念
①两向量的夹角②两向量的数量积
已知空间两个非零向量a,b,则|a|·|b|·cos
(2)空间向量数量积的运算律
①结合律:(λa)·b=λ(a·b);
②交换律:a·b=b·a;
③分配律:a·(b+c)=a·b+a·c.知识网络要点梳理5.向量的坐标运算 知识网络要点梳理?b.如图②③,n1,n2分别是二面角α-l-β的两个半平面α,β的法向量,则二面角的大小θ满足cos θ=cos
(3)若ka+b与ka-2b互相垂直,求实数k的值.专题归纳高考体验(2)∵a=(1,1,0),b=(-1,0,2),
∴a·b=(1,1,0)·(-1,0,2)=-1. (3)法一:∵ka+b=(k-1,k,2),ka-2b=(k+2,k,-4),且ka+b与ka-2b互相垂直,∴(k-1,k,2)·(k+2,k,-4)=(k-1)(k+2)+k2-8=0.专题归纳高考体验反思感悟数量积的应用
(1)求夹角:设向量a,b所成的角为θ,则cos θ= ,进而可求两异面直线所成的角.
(2)求长度(距离):运用公式|a|2=a·a,可使线段长度的计算问题转化为向量数量积的计算问题.
(3)解决垂直问题:利用a⊥b?a·b=0(a≠0,b≠0),可将垂直问题转化为向量数量积的计算问题.专题归纳高考体验跟踪训练1已知空间向量a=(0,-1,1),b=(4,1,0).
(1)若(ka-b)⊥b,则k= .?
(2)若|λa+b|= ,且λ>0,则λ的值为 .?解析(1)因为(ka-b)⊥b,所以(ka-b)·b=0,
即ka·b-|b|2=0,
因此-k-17=0,解得k=-17.
(2)因为a=(0,-1,1),b=(4,1,0),
所以λa+b=λ(0,-1,1)+(4,1,0)=(4,1-λ,λ).
因为|λa+b|= ,所以42+(1-λ)2+λ2=29,
整理得λ2-λ-6=0,解得λ=3或λ=-2,
又因为λ>0,故λ=3.
答案(1)-17 (2)3专题归纳高考体验专题二 利用空间向量证明位置关系
例2 如图所示,在直三棱柱ABC-A1B1C1中,∠ABC=90°,BC=2,CC1=4,EB1=1,D,F,G分别为CC1,B1C1,A1C1的中点,EF与B1D相交于点H.
求证:(1)B1D⊥平面ABD;
(2)平面EGF∥平面ABD.
思路分析建立空间直角坐标系,通过坐标运算,结合线面垂直,面面平行的判定定理进行证明.专题归纳高考体验证明(1)如图所示,建立空间直角坐标系,设A1(a,0,0),
则B1(0,0,0),C1(0,2,0),F(0,1,0),E(0,0,1),A(a,0,4),B(0,0,4),D(0,2,2),G专题归纳高考体验反思感悟向量法证明空间中的位置关系 专题归纳高考体验跟踪训练2如图所示,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB于点F.
求证:(1)PA∥平面EDB;
(2)平面PBD⊥平面EFD.专题归纳高考体验证明以D点为坐标原点, 所在的方向为x,y,z轴建立空间直角坐标系D-xyz(如图所示).设DC=a.
(1)连接AC,交BD于G,连接EG.专题归纳高考体验由已知EF⊥PB,且EF∩DE=E,
所以PB⊥平面EFD.又因为PB?平面PBD,
所以平面PBD⊥平面EFD.专题归纳高考体验专题三 利用空间向量求空间角
例3 (2018全国Ⅰ高考)如图,四边形ABCD为正方形,E,F分别为AD,BC的中点,以DF为折痕把△DFC折起,使点C到达点P的位置,且PF⊥BF.
(1)证明:平面PEF⊥平面ABFD;
(2)求DP与平面ABFD所成角的正弦值.解(1)由已知可得,BF⊥PF,BF⊥EF,
所以BF⊥平面PEF.
又BF?平面ABFD,所以平面PEF⊥平面ABFD.专题归纳高考体验(2)作PH⊥EF,垂足为H.由(1)得,PH⊥平面ABFD.
以H为坐标原点, 的方向为y轴正方向,| |为单位长,建立如图所示的空间直角坐标系H-xyz.专题归纳高考体验反思感悟向量法求解空间角 专题归纳高考体验跟踪训练3如图,正方体ABCD-A1B1C1D1中,M是棱BB1的中点.
(1)求直线A1M与平面AMC1所成角的正弦值.
(2)求二面角A-MC1-A1的余弦值.专题归纳高考体验解以B为坐标原点,BC,BA,BB1所在的直线分别为x轴,y轴,z轴建立空间直角坐标系,专题归纳高考体验专题归纳高考体验考点一 空间向量及其运算
1.(2018全国Ⅱ高考)已知向量a,b满足|a|=1,a·b=-1,则a·(2a-b)=( )
A.4 B.3 C.2 D.0
解析a·(2a-b)=2a2-a·b=2-(-1)=3.
答案B专题归纳高考体验考点二 利用空间向量求空间角 A.30° B.45°
C.60° D.120° 答案A 专题归纳高考体验3.(2019全国Ⅰ高考)如图,直四棱柱ABCD-A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.
(1)证明:MN∥平面C1DE;
(2)求二面角A-MA1-N的正弦值.解(1)连接B1C,ME.
因为M,E分别为BB1,BC的中点,
所以ME∥B1C,且ME= B1C.
又因为N为A1D的中点,所以ND= A1D.
由题设知A1B1??DC,可得B1C??A1D,
故ME??ND,
因此四边形MNDE为平行四边形,MN∥ED.
又MN?平面EDC1,所以MN∥平面C1DE.专题归纳高考体验(2)由已知可得DE⊥DA.
以D为坐标原点, 的方向为x轴正方向,建立如图所示的空间直角坐标系D-xyz,专题归纳高考体验专题归纳高考体验4.(2017课标Ⅱ高考)如图,四棱锥P-ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC= AD,∠BAD=∠ABC=90°,E是PD的中点.
(1)证明:直线CE∥平面PAB;
(2)点M在棱PC上,且直线BM与底面ABCD所成角为45°,求二面角M-AB-D的余弦值.专题归纳高考体验解(1)取PA的中点F,连接EF,BF.
因为E是PD的中点,所以EF∥AD,EF= AD.
由∠BAD=∠ABC=90°得BC∥AD,
又BC= AD,所以EF??BC,四边形BCEF是平行四边形,CE∥BF,
又BF?平面PAB,CE?平面PAB,
故CE∥平面PAB.专题归纳高考体验因为BM与底面ABCD所成的角为45°,
而n=(0,0,1)是底面ABCD的法向量,专题归纳高考体验专题归纳高考体验5.(2019全国Ⅲ高考)图1是由矩形ADEB,Rt△ABC和菱形BFGC组成的一个平面图形,其中AB=1,BE=BF=2,∠FBC=60°.将其沿AB,BC折起使得BE与BF重合,连结DG,如图2.(1)证明:图2中的A,C,G,D四点共面,且平面ABC⊥平面BCGE;
(2)求图2中的二面角B-CG-A的大小. 专题归纳高考体验(1)证明由已知得AD∥BE,CG∥BE,所以AD∥CG,
故AD,CG确定一个平面,从而A,C,G,D四点共面.
由已知得AB⊥BE,AB⊥BC,故AB⊥平面BCGE.
又因为AB?平面ABC,
所以平面ABC⊥平面BCGE.
(2)解作EH⊥BC,垂足为H.
因为EH?平面BCGE,平面BCGE⊥平面ABC,所以EH⊥平面ABC.
由已知,菱形BCGE的边长为2,∠EBC=60°,可求得以H为坐标原点, 的方向为x轴的正方向,建立如图所示的空间直角坐标系H-xyz,专题归纳高考体验专题归纳高考体验6.(2018全国Ⅱ高考)如图,在三棱锥P-ABC中,AB=BC=2 ,PA=PB=PC=AC=4,O为AC的中点.
(1)证明:PO⊥平面ABC;
(2)若点M在棱BC上,且二面角M-PA-C为30°,求PC与平面PAM所成角的正弦值.专题归纳高考体验解(1)因为AP=CP=AC=4,O为AC的中点,所以OP⊥AC,且 由OP2+OB2=PB2知PO⊥OB.
由OP⊥OB,OP⊥AC知PO⊥平面ABC.
(2)如图,以O为坐标原点, 的方向为x轴正方向,建立空间直角坐标系O-xyz.专题归纳高考体验专题归纳高考体验专题归纳高考体验7.(2018北京高考)如图,在三棱柱ABC-A1B1C1中,CC1⊥平面ABC,D,E,F,G分别为AA1,AC,A1C1,BB1的中点,AB=BC= ,AC=AA1=2.
(1)求证:AC⊥平面BEF;
(2)求二面角B-CD-C1的余弦值;
(3)证明:直线FG与平面BCD相交.(1)证明在三棱柱ABC-A1B1C1中,
∵CC1⊥平面ABC,
∴四边形A1ACC1为矩形.
又E,F分别为AC,A1C1的中点,
∴AC⊥EF.∵AB=BC,
∴AC⊥BE,∴AC⊥平面BEF.专题归纳高考体验(2)解由(1)知AC⊥EF,AC⊥BE,EF∥CC1.
∵CC1⊥平面ABC,∴EF⊥平面ABC.
∵BE?平面ABC,∴EF⊥BE.
建立如图所示的空间直角坐标系E-xyz.专题归纳高考体验专题归纳高考体验考点三 利用空间向量解决综合问题
8.(2018天津高考)如图,AD∥BC且AD=2BC,AD⊥CD,EG∥AD且EG=AD,CD∥FG且CD=2FG,DG⊥平面ABCD,DA=DC=DG=2.
(1)若M为CF的中点,N为EG的中点,求证:MN∥平面CDE;
(2)求二面角E-BC-F的正弦值;
(3)若点P在线段DG上,且直线BP与平面ADGE所成的角为60°,求线段DP的长.专题归纳高考体验专题归纳高考体验专题归纳高考体验专题归纳高考体验9.(2019北京高考)如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD⊥CD,AD∥BC,PA=AD=CD=2,BC=3.E为PD的中点,点F在PC上,且 .
(1)求证:CD⊥平面PAD;
(2)求二面角F-AE-P的余弦值;
(3)设点G在PB上,且 ,判断直线AG是否在平面AEF内,说明理由.专题归纳高考体验(1)证明因为PA⊥平面ABCD,所以PA⊥CD.
又因为AD⊥CD,所以CD⊥平面PAD.
(2)解过A作AD的垂线交BC于点M.
因为PA⊥平面ABCD,
所以PA⊥AM,PA⊥AD.
如图建立空间直角坐标系A-xyz,则A(0,0,0),B(2,-1,0),C(2,2,0),D(0,2,0),P(0,0,2).
因为E为PD的中点,所以E(0,1,1).专题归纳高考体验令z=1,则y=-1,x=-1.
于是n=(-1,-1,1).
又因为平面PAD的法向量为p=(1,0,0),专题归纳高考体验
