高中数学新人教A版选修2-1课件:习题课——空间向量在空间问题中的综合应用(38张)
文档属性
| 名称 | 高中数学新人教A版选修2-1课件:习题课——空间向量在空间问题中的综合应用(38张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-20 21:49:44 | ||
图片预览











文档简介
课件38张PPT。习题课——空间向量在空间问题中的综合应用1.利用空间向量求两点间距离
设A(x1,y1,z1),B(x2,y2,z2)为空间中任意两点,则2.利用空间向量求点面距
如图,设AB为过平面α内一点A的一条斜线段,n为平面α的法向量,则点B到平面α的距离d= .3.利用空间向量解决探索性问题
立体几何探索性问题是近几年高考和各地模拟考试中的热点题型.空间向量作为一种工具,在解决立体几何探索性问题中有着无比的优越性,运用空间向量法解题,可使几何问题代数化,大大简化思维程序,使解题思路直观明了.
空间中的探索性问题一般有以下两种类型:
(1)“条件探索型”,就是指给出了问题的明确结论,但条件不足或未知,需要解题者探求、寻找使结论成立的条件的一类问题,这类问题的常用解法是逆推法,利用结论探求条件.
(2)“存在型”,是指结论不确定的问题,即在数学命题中,结论常以“是否存在”的形式出现,其结果可能存在,需要找出来;可能不存在,则需要说明理由.解答这一类问题时,先假设结论存在,若推证无矛盾,则结论存在;若推证出矛盾,则结论不存在.【做一做1】 已知空间两点A,B的坐标分别为(1,-1,1),(2,2,-2),则A,B两点的距离为 .?【做一做2】 如图,在正方体ABCD-A1B1C1D1中,下面结论错误的是( )
A.BD∥平面CB1D1
B.AC1⊥BD
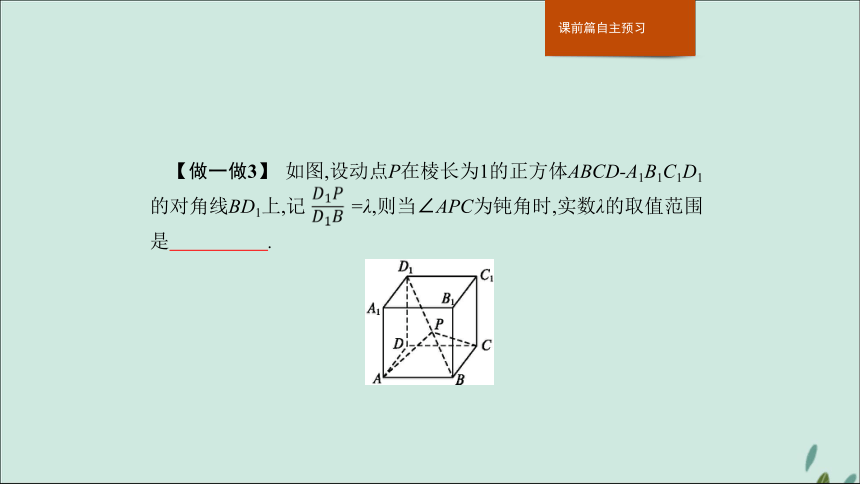
C.AC1⊥平面CB1D1解析以D为原点,DA,DC,DD1分别为x,y,z轴建立空间直角坐标系,不妨设正方体的棱长为1,则有A(1,0,0),B(1,1,0),C(0,1,0),D(0,0,0),A1(1,0,1),B1(1,1,1),C1(0,1,1),D1(0,0,1).答案D 【做一做3】 如图,设动点P在棱长为1的正方体ABCD-A1B1C1D1的对角线BD1上,记 =λ,则当∠APC为钝角时,实数λ的取值范围是 .?解析由题意,建立如图所示的空间直角坐标系D-xyz,则有A(1,0,0),B(1,1,0),C(0,1,0),D1(0,0,1),探究一探究二探究三当堂检测探究一利用空间向量求空间中两点间距离 例1 如图,60°的二面角的棱上有A,B两点,直线AC,BD分别在两个半平面内,且都垂直于AB.若|AB|=1,|AC|=2,|BD|=3,求CD的长度.思路分析本题中的图形不适合建立空间直角坐标系,因此可通过向量分解的方法,利用公式|a|= 求解.探究一探究二探究三当堂检测反思感悟利用空间向量求空间两点距离的基本方法
(1)坐标法,建立空间直角坐标系,得出两个点的坐标,然后根据两点距离公式求解.
(2)向量分解法,将两点所对应向量用基向量表示,然后利用公式|a|= 求解.探究一探究二探究三当堂检测变式训练1已知AB,BC,CD为两两垂直的三条线段,且它们的长都为2,则AD的长为( )
A.4 B.2
C.3 D.2 答案D 探究一探究二探究三当堂检测探究二利用空间向量求点面距
例2 在三棱锥S-ABC中,△ABC是边长为4的正三角形,平面SAC⊥平面ABC,SA=SC=2 ,M,N分别为AB,SB的中点,如图所示.求点B到平面CMN的距离.思路分析借助平面SAC⊥平面ABC的性质,建立空间直角坐标系,先求平面CMN的法向量,再求距离.探究一探究二探究三当堂检测解取AC的中点O,连接OS,OB.
∵SA=SC,AB=BC,
∴AC⊥SO,AC⊥BO.
∵平面SAC⊥平面ABC,平面SAC∩平面ABC=AC,
∴SO⊥平面ABC.
又BO?平面ABC,∴SO⊥BO.
如图所示,分别以OA,OB,OS所在直线为x轴,y轴,z轴,建立空间直角坐标系Oxyz,探究一探究二探究三当堂检测探究一探究二探究三当堂检测反思感悟求点到平面的距离的主要方法
(1)作点到平面的垂线,点到垂足的距离即为点到平面的距离.
(2)在三棱锥中用等体积法求解.
(3)向量法:d= (n为平面的法向量,A为平面上一点,MA为过点A的斜线段)探究一探究二探究三当堂检测变式训练2在直三棱柱中,AA1=AB=BC=3,AC=2,D是AC的中点.
(1)求证:B1C∥平面A1BD;
(2)求点B1到平面A1BD的距离.探究一探究二探究三当堂检测(1)证明连接AB1交A1B于点E,连接DE. 探究一探究二探究三当堂检测探究三利用空间向量解决空间中的探索性问题 例3 在四棱锥P-ABCD中,ABCD是菱形,∠ABC=60°,PA=AC=a,PB=PD= a,点E在PD上,且PE∶ED=2∶1.在PC上是否存在一点F,使BF∥平面AEC?并证明你的结论.
思路分析首先假设存在,然后再根据BF∥平面AEC,结合线面平行的条件进行推理.解∵PA=AC=a,∠ABC=60°,∴AB=AD=a.
又∵PB=PD= a,
∴PA⊥AB,PA⊥AD,
∴PA⊥平面ABCD.如图,以A为坐标原点,AD,AP所在直线分别为y轴、z轴,过A点垂直于平面PAD的直线为x轴,建立空间直角坐标系.探究一探究二探究三当堂检测探究一探究二探究三当堂检测探究一探究二探究三当堂检测反思感悟立体几何中探索性问题的解法
解决这类探索性问题的基本策略是:假定题中的数学对象存在(或结论成立)或暂且认可其中的一部分的结论,然后在这个前提下进行逻辑推理,若由此导出矛盾,则否定假设;否则,给出肯定结论.其中反证法在解题中起着重要的作用.探究一探究二探究三当堂检测变式训练3如图所示,四棱锥P-ABCD中,PA⊥菱形ABCD所在的平面,∠ABC=60°,E是BC中点,F是PC上的点. (1)求证:平面AEF⊥平面PAD;
(2)若M是PD的中点,当AB=AP时,是否存在点F,使直线EM与平面AEF所成角的正弦值为 ?若存在,请求出 的值,若不存在,请说明理由.探究一探究二探究三当堂检测(1)证明连接AC,因为底面ABCD为菱形,∠ABC=60°,所以△ABC是正三角形,
∵E是BC的中点,∴AE⊥BC,
又AD∥BC,∴AE⊥AD,
∵PA⊥平面ABCD,AE?平面ABCD,∴PA⊥AE,
又PA∩AD=A,∴AE⊥平面PAD,
又AE?平面AEF,所以平面AEF⊥平面PAD.
(2)解以A为坐标原点建立如图所示空间直角坐标系,不妨设AB=AP=2,则AE= ,探究一探究二探究三当堂检测探究一探究二探究三当堂检测规范解答
利用空间向量解决空间的综合问题典例如图,直棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB= AB.
(1)证明:BC1∥平面A1CD.
(2)求二面角D-A1C-E的正弦值.
【审题策略】第一问可借助线面平行的判定定理证明;第二问应建立直角坐标系,利用向量方法进行求解.探究一探究二探究三当堂检测【规范展示】
(1)证明连接AC1,交A1C于点F,连接DF,
则F为AC1的中点.
又因为D是AB的中点,所以DF∥BC1.
又因为DF?平面A1CD,BC1?平面A1CD,
故BC1∥平面A1CD.
(2)解设AB=2a,由AA1=AC=CB= AB可得AA1=AC=CB= a,所以AC⊥BC.
又因为ABC-A1B1C1是直三棱柱,
故可建立如图所示的空间直角坐标系.探究一探究二探究三当堂检测探究一探究二探究三当堂检测【答题模板】
第1步:证明线线平行
?
第2步:证得线面平行
?
第3步:建立空间直角坐标系
?
第4步:求出平面内两不共线向量的坐标
?
第5步:用待定系数法求法向量的坐标
?
第6步:求出两个法向量夹角的余弦值,进而求得正弦值.探究一探究二探究三当堂检测失误警示通过阅卷统计分析,失分主要出现在第(2)问,造成失分的原因是:
(1)不能利用三角形中的边长关系找到垂直的条件,从而不能恰当地建立空间直角坐标系.
(2)不能利用中点公式正确地求出相关点的坐标.
(3)待定系数法求法向量的方法与步骤不熟练,导致法向量坐标求错.
(4)不能利用三角函数的知识把向量夹角的余弦值转化为二面角的正弦值.探究一探究二探究三当堂检测 跟踪训练
如图,在多面体ABCDEF中,正方形ADEF与梯形ABCD所在平面互相垂直,AB∥CD,AD⊥CD,AB=AD=1,CD=2,M,N分别为EC和BD的中点.
(1)求证:BC⊥平面BDE;
(2)求直线MN与平面BMC所成的角的正弦值.探究一探究二探究三当堂检测(1)证明在梯形ABCD中,取CD中点H,连接BH,
因为AD=AB,AB∥CD,AD⊥CD,
所以四边形ADHB为正方形.
又BD2=AD2+AB2=2,BC2=HC2+HB2=2,
所以CD2=BD2+BC2,所以BC⊥BD.
又平面ADEF⊥平面ABCD,平面ADEF∩平面ABCD=AD,DE⊥AD,
所以DE⊥平面ABCD,所以BC⊥DE,
又BD∩DE=D,故BC⊥平面BDE.探究一探究二探究三当堂检测(2)解由(1)知CD⊥平面ABCD,AD⊥CD,
所以DE,DA,DC两两垂直.
以D为坐标原点建立如图所示直角坐标系D-xyz,探究一探究二探究三当堂检测1.在四面体P-ABC中,PA,PB,PC两两垂直,M是面ABC内一点,且M到其他三面的距离分别是2,3,6,则M到顶点P的距离是( )
A.7 B.8 C.9 D.10
解析以P为原点,PA,PB,PC所在直线分别为x轴,y轴,z轴建立空间直角坐标系,由已知M(2,3,6),所以|MP|= .
答案A探究一探究二探究三当堂检测2.在如图所示的几何体中,三棱锥D-ABC的各条棱长均为2,OA,OB,OC两两垂直,则下列说法正确的是( )
A.OA,OB,OC的长度可以不相等
B.直线OB∥平面ACD
C.直线OD与BC所成的角是45°
D.直线AD与OB所成的角是45°探究一探究二探究三当堂检测答案D 探究一探究二探究三当堂检测3.如图所示,在直二面角α-l-β中,A,B∈l,AC?α,AC⊥l,BD?β,BD⊥l,AC=6,AB=8,BD=24,则线段CD的长为 .?答案26 探究一探究二探究三当堂检测4.已知三棱锥A-BCD,AD⊥AB,AB=AD,△BDC是边长为2 的等边三角形.
(1)证明:BD⊥AC.
(2)若平面ABD⊥平面ABC,求二面角A-BC-D的余弦值.(1)证明设E为BD中点,连接AE,EC.
因为AB=AD,所以BD⊥AE.
又因为△BDC是等边三角形,所以BD⊥CE.
又CE∩AE=E,故BD⊥平面AEC.
所以BD⊥AC.探究一探究二探究三当堂检测(2)解因为平面ABD⊥平面ABC,且相交于AB,又AD⊥AB,
所以AD⊥平面ABC.
以A为坐标原点,AC,AB,AD所在的直线分别为x,y,z轴建立空间直角坐标系A-xyz,则A(0,0,0),B(0,2,0),C(2,0,0),D(0,0,2),
设A(x1,y1,z1),B(x2,y2,z2)为空间中任意两点,则2.利用空间向量求点面距
如图,设AB为过平面α内一点A的一条斜线段,n为平面α的法向量,则点B到平面α的距离d= .3.利用空间向量解决探索性问题
立体几何探索性问题是近几年高考和各地模拟考试中的热点题型.空间向量作为一种工具,在解决立体几何探索性问题中有着无比的优越性,运用空间向量法解题,可使几何问题代数化,大大简化思维程序,使解题思路直观明了.
空间中的探索性问题一般有以下两种类型:
(1)“条件探索型”,就是指给出了问题的明确结论,但条件不足或未知,需要解题者探求、寻找使结论成立的条件的一类问题,这类问题的常用解法是逆推法,利用结论探求条件.
(2)“存在型”,是指结论不确定的问题,即在数学命题中,结论常以“是否存在”的形式出现,其结果可能存在,需要找出来;可能不存在,则需要说明理由.解答这一类问题时,先假设结论存在,若推证无矛盾,则结论存在;若推证出矛盾,则结论不存在.【做一做1】 已知空间两点A,B的坐标分别为(1,-1,1),(2,2,-2),则A,B两点的距离为 .?【做一做2】 如图,在正方体ABCD-A1B1C1D1中,下面结论错误的是( )
A.BD∥平面CB1D1
B.AC1⊥BD
C.AC1⊥平面CB1D1解析以D为原点,DA,DC,DD1分别为x,y,z轴建立空间直角坐标系,不妨设正方体的棱长为1,则有A(1,0,0),B(1,1,0),C(0,1,0),D(0,0,0),A1(1,0,1),B1(1,1,1),C1(0,1,1),D1(0,0,1).答案D 【做一做3】 如图,设动点P在棱长为1的正方体ABCD-A1B1C1D1的对角线BD1上,记 =λ,则当∠APC为钝角时,实数λ的取值范围是 .?解析由题意,建立如图所示的空间直角坐标系D-xyz,则有A(1,0,0),B(1,1,0),C(0,1,0),D1(0,0,1),探究一探究二探究三当堂检测探究一利用空间向量求空间中两点间距离 例1 如图,60°的二面角的棱上有A,B两点,直线AC,BD分别在两个半平面内,且都垂直于AB.若|AB|=1,|AC|=2,|BD|=3,求CD的长度.思路分析本题中的图形不适合建立空间直角坐标系,因此可通过向量分解的方法,利用公式|a|= 求解.探究一探究二探究三当堂检测反思感悟利用空间向量求空间两点距离的基本方法
(1)坐标法,建立空间直角坐标系,得出两个点的坐标,然后根据两点距离公式求解.
(2)向量分解法,将两点所对应向量用基向量表示,然后利用公式|a|= 求解.探究一探究二探究三当堂检测变式训练1已知AB,BC,CD为两两垂直的三条线段,且它们的长都为2,则AD的长为( )
A.4 B.2
C.3 D.2 答案D 探究一探究二探究三当堂检测探究二利用空间向量求点面距
例2 在三棱锥S-ABC中,△ABC是边长为4的正三角形,平面SAC⊥平面ABC,SA=SC=2 ,M,N分别为AB,SB的中点,如图所示.求点B到平面CMN的距离.思路分析借助平面SAC⊥平面ABC的性质,建立空间直角坐标系,先求平面CMN的法向量,再求距离.探究一探究二探究三当堂检测解取AC的中点O,连接OS,OB.
∵SA=SC,AB=BC,
∴AC⊥SO,AC⊥BO.
∵平面SAC⊥平面ABC,平面SAC∩平面ABC=AC,
∴SO⊥平面ABC.
又BO?平面ABC,∴SO⊥BO.
如图所示,分别以OA,OB,OS所在直线为x轴,y轴,z轴,建立空间直角坐标系Oxyz,探究一探究二探究三当堂检测探究一探究二探究三当堂检测反思感悟求点到平面的距离的主要方法
(1)作点到平面的垂线,点到垂足的距离即为点到平面的距离.
(2)在三棱锥中用等体积法求解.
(3)向量法:d= (n为平面的法向量,A为平面上一点,MA为过点A的斜线段)探究一探究二探究三当堂检测变式训练2在直三棱柱中,AA1=AB=BC=3,AC=2,D是AC的中点.
(1)求证:B1C∥平面A1BD;
(2)求点B1到平面A1BD的距离.探究一探究二探究三当堂检测(1)证明连接AB1交A1B于点E,连接DE. 探究一探究二探究三当堂检测探究三利用空间向量解决空间中的探索性问题 例3 在四棱锥P-ABCD中,ABCD是菱形,∠ABC=60°,PA=AC=a,PB=PD= a,点E在PD上,且PE∶ED=2∶1.在PC上是否存在一点F,使BF∥平面AEC?并证明你的结论.
思路分析首先假设存在,然后再根据BF∥平面AEC,结合线面平行的条件进行推理.解∵PA=AC=a,∠ABC=60°,∴AB=AD=a.
又∵PB=PD= a,
∴PA⊥AB,PA⊥AD,
∴PA⊥平面ABCD.如图,以A为坐标原点,AD,AP所在直线分别为y轴、z轴,过A点垂直于平面PAD的直线为x轴,建立空间直角坐标系.探究一探究二探究三当堂检测探究一探究二探究三当堂检测探究一探究二探究三当堂检测反思感悟立体几何中探索性问题的解法
解决这类探索性问题的基本策略是:假定题中的数学对象存在(或结论成立)或暂且认可其中的一部分的结论,然后在这个前提下进行逻辑推理,若由此导出矛盾,则否定假设;否则,给出肯定结论.其中反证法在解题中起着重要的作用.探究一探究二探究三当堂检测变式训练3如图所示,四棱锥P-ABCD中,PA⊥菱形ABCD所在的平面,∠ABC=60°,E是BC中点,F是PC上的点. (1)求证:平面AEF⊥平面PAD;
(2)若M是PD的中点,当AB=AP时,是否存在点F,使直线EM与平面AEF所成角的正弦值为 ?若存在,请求出 的值,若不存在,请说明理由.探究一探究二探究三当堂检测(1)证明连接AC,因为底面ABCD为菱形,∠ABC=60°,所以△ABC是正三角形,
∵E是BC的中点,∴AE⊥BC,
又AD∥BC,∴AE⊥AD,
∵PA⊥平面ABCD,AE?平面ABCD,∴PA⊥AE,
又PA∩AD=A,∴AE⊥平面PAD,
又AE?平面AEF,所以平面AEF⊥平面PAD.
(2)解以A为坐标原点建立如图所示空间直角坐标系,不妨设AB=AP=2,则AE= ,探究一探究二探究三当堂检测探究一探究二探究三当堂检测规范解答
利用空间向量解决空间的综合问题典例如图,直棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB= AB.
(1)证明:BC1∥平面A1CD.
(2)求二面角D-A1C-E的正弦值.
【审题策略】第一问可借助线面平行的判定定理证明;第二问应建立直角坐标系,利用向量方法进行求解.探究一探究二探究三当堂检测【规范展示】
(1)证明连接AC1,交A1C于点F,连接DF,
则F为AC1的中点.
又因为D是AB的中点,所以DF∥BC1.
又因为DF?平面A1CD,BC1?平面A1CD,
故BC1∥平面A1CD.
(2)解设AB=2a,由AA1=AC=CB= AB可得AA1=AC=CB= a,所以AC⊥BC.
又因为ABC-A1B1C1是直三棱柱,
故可建立如图所示的空间直角坐标系.探究一探究二探究三当堂检测探究一探究二探究三当堂检测【答题模板】
第1步:证明线线平行
?
第2步:证得线面平行
?
第3步:建立空间直角坐标系
?
第4步:求出平面内两不共线向量的坐标
?
第5步:用待定系数法求法向量的坐标
?
第6步:求出两个法向量夹角的余弦值,进而求得正弦值.探究一探究二探究三当堂检测失误警示通过阅卷统计分析,失分主要出现在第(2)问,造成失分的原因是:
(1)不能利用三角形中的边长关系找到垂直的条件,从而不能恰当地建立空间直角坐标系.
(2)不能利用中点公式正确地求出相关点的坐标.
(3)待定系数法求法向量的方法与步骤不熟练,导致法向量坐标求错.
(4)不能利用三角函数的知识把向量夹角的余弦值转化为二面角的正弦值.探究一探究二探究三当堂检测 跟踪训练
如图,在多面体ABCDEF中,正方形ADEF与梯形ABCD所在平面互相垂直,AB∥CD,AD⊥CD,AB=AD=1,CD=2,M,N分别为EC和BD的中点.
(1)求证:BC⊥平面BDE;
(2)求直线MN与平面BMC所成的角的正弦值.探究一探究二探究三当堂检测(1)证明在梯形ABCD中,取CD中点H,连接BH,
因为AD=AB,AB∥CD,AD⊥CD,
所以四边形ADHB为正方形.
又BD2=AD2+AB2=2,BC2=HC2+HB2=2,
所以CD2=BD2+BC2,所以BC⊥BD.
又平面ADEF⊥平面ABCD,平面ADEF∩平面ABCD=AD,DE⊥AD,
所以DE⊥平面ABCD,所以BC⊥DE,
又BD∩DE=D,故BC⊥平面BDE.探究一探究二探究三当堂检测(2)解由(1)知CD⊥平面ABCD,AD⊥CD,
所以DE,DA,DC两两垂直.
以D为坐标原点建立如图所示直角坐标系D-xyz,探究一探究二探究三当堂检测1.在四面体P-ABC中,PA,PB,PC两两垂直,M是面ABC内一点,且M到其他三面的距离分别是2,3,6,则M到顶点P的距离是( )
A.7 B.8 C.9 D.10
解析以P为原点,PA,PB,PC所在直线分别为x轴,y轴,z轴建立空间直角坐标系,由已知M(2,3,6),所以|MP|= .
答案A探究一探究二探究三当堂检测2.在如图所示的几何体中,三棱锥D-ABC的各条棱长均为2,OA,OB,OC两两垂直,则下列说法正确的是( )
A.OA,OB,OC的长度可以不相等
B.直线OB∥平面ACD
C.直线OD与BC所成的角是45°
D.直线AD与OB所成的角是45°探究一探究二探究三当堂检测答案D 探究一探究二探究三当堂检测3.如图所示,在直二面角α-l-β中,A,B∈l,AC?α,AC⊥l,BD?β,BD⊥l,AC=6,AB=8,BD=24,则线段CD的长为 .?答案26 探究一探究二探究三当堂检测4.已知三棱锥A-BCD,AD⊥AB,AB=AD,△BDC是边长为2 的等边三角形.
(1)证明:BD⊥AC.
(2)若平面ABD⊥平面ABC,求二面角A-BC-D的余弦值.(1)证明设E为BD中点,连接AE,EC.
因为AB=AD,所以BD⊥AE.
又因为△BDC是等边三角形,所以BD⊥CE.
又CE∩AE=E,故BD⊥平面AEC.
所以BD⊥AC.探究一探究二探究三当堂检测(2)解因为平面ABD⊥平面ABC,且相交于AB,又AD⊥AB,
所以AD⊥平面ABC.
以A为坐标原点,AC,AB,AD所在的直线分别为x,y,z轴建立空间直角坐标系A-xyz,则A(0,0,0),B(0,2,0),C(2,0,0),D(0,0,2),
