第2章 4 二次函数性质的再研究
图片预览




文档简介
§4 二次函数性质的再研究
学习目标 1.掌握配方法,理解a,b,c(或a,h,k)对二次函数图像的作用.2.理解由y=x2到y=a(x+h)2+k的图像变换方法.3.能根据条件灵活选择二次函数的三种形式求解析式.4.掌握二次函数的性质.
知识点一 二次函数的配方法
思考 y=4x2-4x-1如何配方?你能由此求出方程4x2-4x-1=0的根吗?
答案 y=4(x2-x)-1=4-1
=42-2.
令y=0,即4x2-4x-1=0,
42-2=0,
2=,
x=±=.
梳理 对于一般的二次函数y=ax2+bx+c(a≠0),可类似地配方为y=a2+,由此可得二次函数的值域、顶点等性质,y=x2与y=ax2+bx+c图像间的关系以及二次方程求根公式等.所以配方法是非常重要的数学方法.
知识点二 图像变换
思考 y=x2和y=2(x+1)2+3的图像之间有什么关系?
答案 y=x2的图像各点纵坐标变为原来的2倍,可得y=2x2的图像;再把y=2x2的图像向左平移1个单位长度,再上平移3个单位长度,得y=2(x+1)2+3的图像.
梳理 由y=x2的图像各点纵坐标变为原来的a倍,左移个单位长度,上移个单位长度,可得y=a2+的图像,即y=ax2+bx+c的图像.
知识点三 二次函数的三种形式
思考 我们知道y=x2-2x=(x-1)2-1=(x-2)x,那么点(1,-1),数0,2是y=x2-2x的什么?
答案 点(1,-1)是y=x2-2x的顶点,数0,2是方程x2-2x=0的两根.
梳理 (1)二次函数的一般式y=ax2+bx+c(a≠0).
(2)如果已知二次函数的顶点坐标为(-h,k),则可将二次函数设为y=a(x+h)2+k.
(3)如果已知方程ax2+bx+c=0的两根x1,x2(即抛物线与x轴交点横坐标),可设为y=a(x-x1)(x-x2).
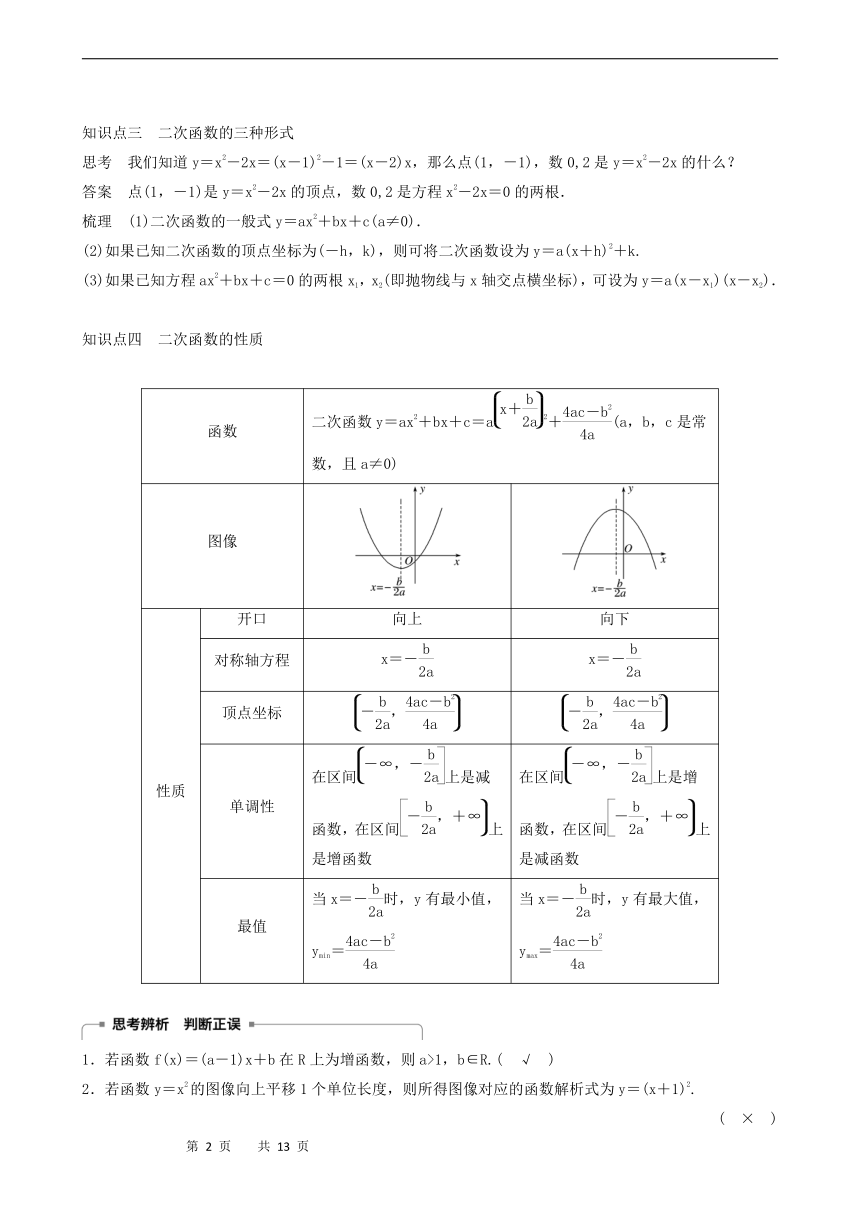
知识点四 二次函数的性质
函数
二次函数y=ax2+bx+c=a2+(a,b,c是常数,且a≠0)
图像
性质
开口
向上
向下
对称轴方程
x=-
x=-
顶点坐标
单调性
在区间上是减函数,在区间上是增函数
在区间上是增函数,在区间上是减函数
最值
当x=-时,y有最小值,ymin=
当x=-时,y有最大值,ymax=
1.若函数f(x)=(a-1)x+b在R上为增函数,则a>1,b∈R.( √ )
2.若函数y=x2的图像向上平移1个单位长度,则所得图像对应的函数解析式为y=(x+1)2.
( × )
3.二次函数y=x2与y=3x2的图像的形状相同.( × )
类型一 二次函数解析式的求解
例1 已知二次函数y=ax2+bx+c(a≠0)的图像与x轴相交于点A(-3,0),对称轴为x=-1,顶点M到x轴的距离为2,求此函数的解析式.
考点 二次函数解析式求法
题点 一般式求法
解 方法一 代入A(-3,0),
有9a-3b+c=0,①
由对称轴为x=-1,得-=-1,②
顶点M到x轴的距离为|a-b+c-0|=2,③
联立①②③解得或
所以此函数的解析式为y=x2+x-或y=-x2-x+.
考点 二次函数解析式求法
题点 顶点式求法
方法二 因为二次函数图像的对称轴是x=-1,
又顶点M到x轴的距离为2,所以顶点的坐标为(-1,2)或(-1,-2),
故可得二次函数的解析式为y=a(x+1)2+2或y=a(x+1)2-2.
因为图像过点A(-3,0),所以0=a(-3+1)2+2或0=a(-3+1)2-2,解得a=-或a=.
故所求二次函数的解析式为y=-(x+1)2+2=-x2-x+或y=(x+1)2-2=x2+x-.
考点 二次函数解析式的求法
题点 两根式求法
方法三 因为二次函数图像的对称轴为x=-1,
又图像过点A(-3,0),所以点A关于对称轴的对称点A′(1,0)也在图像上,
所以可得二次函数的解析式为y=a(x+3)(x-1).
由题意得顶点坐标为(-1,2)或(-1,-2),
分别代入上式,解得a=-或a=.
故所求二次函数的解析式为y=-(x+3)(x-1)=-x2-x+或y=(x+3)(x-1)=x2+x-.
反思与感悟 求二次函数解析式的步骤
跟踪训练1 (1)y=ax2+6x-8与直线y=-3x交于点A(1,m),求a.
考点 二次函数解析式的求法
题点 一般式求法
解 把A(1,m)代入y=-3x,得m=-3,
把(1,-3)代入y=ax2+6x-8,得
a+6-8=-3,即a=-1.
(2)f(x)=x2+bx+c,若f(-4)=f(0),f(-2)=-2,求f(x).
考点 二次函数解析式求法
题点 顶点式求法
解 方法一 由f(-4)=f(0),知f(x)的对称轴为
x==-2,
又f(-2)=-2,∴顶点坐标为(-2,-2),
∴f(x)=(x+2)2-2=x2+4x+2.
考点 二次函数解析式的求法
题点 两根式求法
方法二 由f(-4)=f(0),可设f(x)=x(x+4)+c.
代入x=-2,得-2×(-2+4)+c=-2,∴c=2.
∴f(x)=x2+4x+2.
类型二 二次函数的图像及变换
例2 由函数y=x2的图像如何得到f(x)=-x2+2x+3的图像.
考点 二次函数图像
题点 二次函数图像变换
解 f(x)=-x2+2x+3=-(x2-2x)+3
=-(x2-2x+1-1)+3=-(x-1)2+4,
∴由y=-x2的图象与y=x2的图像关于x轴对称,
可得y=-x2的图像.
由y=-x2的图像向右平移1个单位长度,向上平移4个单位长度,可得y=-(x-1)2+4,即y=-x2+2x+3的图像.
引申探究
利用f(x)=-x2+2x+3的图像比较f(-1),f(2)的大小.
解 f(x)图像如图.
由图知越接近对称轴,函数值越大.
由|-1-1|=2>|2-1|=1,
即f(2)比f(-1)更接近对称轴,∴f(2)>f(-1).
反思与感悟 处理二次函数y=ax2+bx+c(a≠0)的图像问题,主要是考虑其图像特征如开口、顶点、与x轴交点、与y轴交点、对称轴等与系数a,b,c之间的关系.
在图像变换中,记住“h正左移,h负右移,k正上移,k负下移”.
跟踪训练2 将二次函数f(x)=x2+bx+c的图像向左平移2个单位长度,再向上平移3个单位长度,得到二次函数f(x)=x2-2x+1的图像,则b=______,c=______.
考点 二次函数图像
题点 二次函数图像变换
答案 -6 6
解析 f(x)=x2-2x+1=(x-1)2,其图像顶点为(1,0).
将二次函数f(x)=x2-2x+1的图像向下平移3个单位长度,再向右平移2个单位长度后的图像的顶点为(3,-3),得到的抛物线为y=(x-3)2-3,即f(x)=x2+bx+c,
∴(x-3)2-3=x2+bx+c,即x2-6x+6=x2+bx+c,
∴b=-6,c=6.
类型三 二次函数的性质
例3 已知函数f(x)=x2-3x-:
(1)求函数图像的顶点坐标、对称轴方程和最值;
(2)若x∈[1,4],求函数值域.
考点 二次函数性质
题点 由解析式研究二次函数性质
解 (1)对函数右端的表达式配方,得
f(x)=(x-3)2-,
所以函数图像的顶点坐标为,
对称轴方程为x=3,最小值为-,无最大值.
(2)由于3∈[1,4],所以函数在区间[1,3]上是减函数,在区间[3,4]上是增函数,
所以当x=3时,ymin=-,
当x=1时,ymax=×4-=-,
所以函数的值域为.
反思与感悟 解析式、图像、性质三者各有特点又联系紧密,应用时在三者间灵活转化可使问题更易解决.
跟踪训练3 已知函数f(x)=ax2+2ax+1在区间[-1,2]上有最大值4,求实数a的值.
考点 二次函数性质
题点 由性质求参数范围
解 f(x)=a(x+1)2+1-a.
当a=0时,函数f(x)在区间[-1,2]上的值不变,恒为常数1,不符合题意,舍去;
当a>0时,函数f(x)在区间[-1,2]上是增函数,最大值为f(2)=8a+1=4,解得a=;
当a<0时,函数f(x)在区间[-1,2]上是减函数,最大值为f(-1)=1-a=4,解得a=-3.
综上,a的值为-3或.
1.二次函数f(x)=ax2+bx+c(a≠0)与g(x)=bx2+ax+c(b≠0)的图像可能是下图中的( )
考点 二次函数图像
题点 图像与a,b,c的关系
答案 D
解析 由于f(x),g(x)的图像的对称轴方程分别是x=-,x=-,则-与-同号,即f(x),g(x)的图像的对称轴位于y轴的同一侧,由此排除A,B;由C,D中给出的图像,可判定f(x),g(x)的图像的开口方向相反,故ab<0,于是->0,->0,即f(x),g(x)的图像的对称轴都位于y轴右侧,排除C,故选D.
2.设二次函数y=f(x)满足f(4+x)=f(4-x),又f(x)在[4,+∞)上是减函数,且f(a)≥f(0),则实数a的取值范围是( )
A.a≥4 B.0≤a≤8
C.a<0 D.a<0或a≥8
考点 二次函数性质
题点 二次函数性质综合应用
答案 B
解析 由题意知二次函数f(x)的图像关于直线x=4对称,则有f(0)=f(8).因为f(x)在[4,
+∞)上是减函数,所以f(x)在(-∞,4]上是增函数.当a∈(-∞,4]时,由f(a)≥f(0),得0≤a≤4;当a∈[4,+∞)时,由f(a)≥f(0),即f(a)≥f(8),得4≤a≤8.综上可知0≤a≤8.
3.已知f(x)=x2+bx+c,且f(-1)=f(3),则( )
A.f(1)>c>f(-1) B.f(1)C.c>f(-1)>f(1) D.c考点 二次函数性质
题点 二次函数的单调性
答案 B
解析 因为f(-1)=f(3),所以f(x)图像的对称轴为x=1,因此函数在区间(-∞,1]上是减函数,又c=f(0),所以f(1)4.根据下列条件,求二次函数y=f(x)的解析式.
(1)图像过点(2,0),(4,0),(0,3);
(2)图像顶点为(1,2)并且过点(0,4);
(3)过点(1,1),(0,2),(3,5).
考点 二次函数解析式求法
题点 (1)两根式求法
(2)顶点式求法
(3)一般式求法
解 (1)由题意可设二次函数解析式为y=a(x-2)(x-4),
将(0,3)代入得a=.
∴所求二次函数解析式为y=(x-2)(x-4).
(2)由题意可设二次函数解析式为y=a(x-1)2+2,
将(0,4)代入得a=2,
∴所求二次函数解析式为y=2(x-1)2+2.
(3)由题意可设二次函数解析式为y=ax2+bx+c,
将(1,1),(0,2),(3,5)代入得
解得
∴所求二次函数解析式为y=x2-2x+2.
1.配方法是重要的数学方法,在处理二次函数图像变换,研究二次函数性质时使用频繁.
2.二次函数图像变换规律可以推广到一般函数,即:
(1)y=f(x)y=f(x+a);
(2)y=f(x)y=f(x)+b;
(3)y=f(x)y=af(x)(a>0);
(4)y=f(x)y=-f(x);
(5)y=f(x)y=f(-x).
一、选择题
1.函数f(x)=x2+mx+1的图像关于直线x=1对称,则( )
A.m=-2 B.m=2
C.m=-1 D.m=1
考点 二次函数解析式求法
题点 一般式求法
答案 A
解析 二次函数f(x)=x2+mx+1图像的对称轴为x=-,于是-=1,解得m=-2.
2.二次函数y=-x2+4x+t的顶点在x轴上,则t的值是( )
A.-4 B.4
C.-2 D.2
考点 二次函数解析式求法
题点 一般式求法
答案 A
解析 二次函数的图像开口向下,顶点在x轴上,所以对应一元二次方程的Δ=42-4×(-1)t=0,解得t=-4.
3.已知抛物线与x轴交于点(-1,0),(1,0),并且与y轴交于点(0,1),则抛物线的解析式为( )
A.y=-x2+1 B.y=x2+1
C.y=-x2-1 D.y=x2-1
考点 二次函数解析式求法
题点 两根式求法
答案 A
解析 设f(x)=a(x-1)(x+1),
代入(0,1),f(0)=a(0-1)(0+1)=-a=1,
∴a=-1,∴f(x)=1-x2.
4.若一次函数y=ax+b的图像经过第二、三、四象限,则二次函数y=ax2+bx的图像只可能是( )
考点 二次函数图像
题点 图像与a,b,c的关系
答案 C
解析 因为一次函数y=ax+b的图像经过第二、三、四象限,所以a<0,b<0,所以二次函数的图像开口向下,对称轴x=-<0,只有选项C满足.
5.若函数f(x)=x2+ax+b的图像与x轴的交点为(1,0)和(3,0),则函数f(x)( )
A.在(-∞,2]上是减少的,在[2,+∞)上是增加的
B.在(-∞,3)上是增加的
C.在[1,3]上是增加的
D.单调性不能确定
考点 二次函数性质
题点 二次函数单调性
答案 A
解析 由已知可得函数f(x)图像的对称轴为x=2,又二次项系数1>0,所以f(x)在(-∞,2]上是减少的,在[2,+∞)上是增加的.
6.函数y=-x2-2ax(0≤x≤1)的最大值是a2,则实数a的取值范围是( )
A.[0,1]B.[0,2]C.[-2,0]D.[-1,0]
考点 二次函数性质
题点 二次函数在闭区间上的最值
答案 D
解析 y=-(x+a)2+a2,要使ymax=a2,需满足0≤-a≤1,解得-1≤a≤0.
7.已知二次函数y=ax2+bx+c(a≠0)的图像顶点为(2,-1),与y轴交点坐标为(0,11),则( )
A.a=1,b=-4,c=-11
B.a=3,b=12,c=11
C.a=3,b=-6,c=-11
D.a=3,b=-12,c=11
考点 二次函数解析式求法
题点 一般式求法
答案 D
解析 由二次函数的图像与y轴交点坐标为(0,11),知c=11,又因为函数y=ax2+bx+c的图像顶点为(2,-1),所以-=2,=-1,解得a=3,b=-12.
二、填空题
8.函数y=3x2-x+2的图像向左平移1个单位长度,再向下平移2个单位长度,所得图像对应的函数解析式是________________.
考点 二次函数图像
题点 二次函数图像变换
答案 y=3x2+5x+2
解析 函数y=3x2-x+2的图像向左平移1个单位长度,得函数y=3(x+1)2-(x+1)+2的图像,再向下平移2个单位长度,得函数y=3(x+1)2-(x+1)+2-2的图像,即所得图像对应的函数解析式是y=3x2+5x+2.
9.如果函数f(x)=x2+2(a-1)x+2在区间(-∞,4]上是减少的,那么实数a的取值范围是________.
考点 二次函数性质
题点 二次函数单调性
答案 (-∞,-3]
解析 二次函数f(x)的图像开口向上,且对称轴方程为x=1-a,
所以f(x)的递减区间为(-∞,1-a],
故(-∞,4]?(-∞,1-a],因此1-a≥4,解得a≤-3.
10.设f(x)=x2+4x+3,不等式f(x)≥a对x∈R恒成立,则实数a的取值范围是________.
考点 二次函数性质
题点 二次函数最值
答案 (-∞,-1]
解析 f(x)≥a对x∈R恒成立?f(x)min≥a,
f(x)=(x+2)2-1,∴f(x)min=f(-2)=-1,
∴a≤-1.
三、解答题
11.已知二次函数f(x)的图像的对称轴是直线x=1,且f(1)=4,f(4)=-5.
(1)求函数f(x)的解析式,并画出f(x)的图像;
(2)根据图像写出函数f(x)的单调区间,并指明在该区间上的单调性;
(3)当函数f(x)在区间(-∞,m]上是增函数时,求实数m的取值范围.
考点 二次函数图像与性质
题点 图像性质综合应用
解 (1)设f(x)=ax2+bx+c(a≠0),由题意得
解得
所以函数f(x)=-x2+2x+3,f(x)的图像如图所示.
(2)由图像可得函数f(x)的单调区间是(-∞,1]和[1,+∞),其中函数f(x)在区间(-∞,1]上是增加的,在区间[1,+∞)上是减少的.
(3)由(2)知函数f(x)=-x2+2x+3在区间(-∞,1]上是增函数,那么(-∞,m]?(-∞,1],则有m≤1.
12.二次函数f(x)与g(x)的图像开口大小相同,开口方向也相同.已知函数g(x)的解析式和f(x)图像的顶点,写出函数f(x)的解析式.
(1)函数g(x)=x2,f(x)图像的顶点是(4,-7);
(2)函数g(x)=-2(x+1)2,f(x)图像的顶点是(-3,2).
考点 二次函数解析式求法
题点 顶点式求法
解 (1)因为f(x)与g(x)=x2的图像开口大小相同,开口方向也相同,
f(x)图像的顶点是(4,-7),
所以f(x)=(x-4)2-7=x2-8x+9.
(2)由题意知,f(x)的二次项系数为-2,
又因为f(x)图像的顶点是(-3,2),
所以f(x)=-2(x+3)2+2=-2x2-12x-16.
13.某商场以每件42元的价格购进一种服装,根据试营销量得知:这种服装每天的销售量t(t>0,t∈N)(件)与每件的销售价x(x>42,x∈N)(元)之间可看成是一次函数关系:t=-3x+204.
(1)写出商场每天卖这种服装的销售利润y(元)与每件的销售价x(元)之间的函数关系式(每天的销售利润是指所卖出服装的总销售所得与购进这些服装所花费金额的差);
(2)通过对所得函数关系式进行配方,指出:商场要想每天获得最大的销售利润,每件的销售价定为多少最为合适?最大销售利润为多少?
考点 二次函数性质
题点 二次函数最值
解 (1)由题意得,每天的销售利润y(元)与每件的销售价x(元)之间的函数关系式为y=(x-42)(-3x+204)=-3x2+330x-8568(42(2)由(1)得y=-3(x-55)2+507(42即当每件的销售价定为55元时,每天可获得最大的销售利润,最大销售利润为507元.
四、探究与拓展
14.已知二次函数y=ax2+bx+c(a≠0)的图像如图所示,则下列结论中正确的是( )
A.a>0
B.当x>1时,y随x的增大而增大
C.c<0
D.3是方程ax2+bx+c=0的一个根
考点 二次函数图像
题点 二次函数图像与性质关系
答案 D
解析 从二次函数的图像可知,图像开口向下,a<0;当x>1时,y随x的增大而减小;当x=0时,y=c>0;二次函数图像的对称轴为直线x=1,函数图像与x轴的一个交点的横坐标为-1,则根据对称性,函数图像与x轴的另一个交点的横坐标为3.故选D.
15.已知函数f(x)=x2+2ax+3,x∈[-4,6].
(1)当a=-2时,求f(x)的最值;
(2)求实数a的取值范围,使y=f(x)在区间[-4,6]上是单调函数;
(3)当a=1时,求f(|x|)的单调区间.
考点 二次函数性质
题点 二次函数性质综合
解 (1)当a=-2时,f(x)=x2-4x+3=(x-2)2-1,
由于x∈[-4,6],∴f(x)在区间[-4,2]上是减少的,在区间[2,6]上是增加的,∴f(x)的最小值是f(2)=-1,
又f(-4)=35,f(6)=15,
∴f(x)的最大值是35.
(2)∵函数f(x)的图像开口向上,对称轴是x=-a,
∴要使f(x)在区间[-4,6]上是单调函数,
应有-a≤-4或-a≥6,即a≤-6或a≥4.
(3)当a=1时,f(x)=x2+2x+3,
∴f(|x|)=x2+2|x|+3,此时定义域为x∈[-6,6],
且f(x)=
∴f(|x|)的递增区间是(0,6],递减区间是[-6,0].
学习目标 1.掌握配方法,理解a,b,c(或a,h,k)对二次函数图像的作用.2.理解由y=x2到y=a(x+h)2+k的图像变换方法.3.能根据条件灵活选择二次函数的三种形式求解析式.4.掌握二次函数的性质.
知识点一 二次函数的配方法
思考 y=4x2-4x-1如何配方?你能由此求出方程4x2-4x-1=0的根吗?
答案 y=4(x2-x)-1=4-1
=42-2.
令y=0,即4x2-4x-1=0,
42-2=0,
2=,
x=±=.
梳理 对于一般的二次函数y=ax2+bx+c(a≠0),可类似地配方为y=a2+,由此可得二次函数的值域、顶点等性质,y=x2与y=ax2+bx+c图像间的关系以及二次方程求根公式等.所以配方法是非常重要的数学方法.
知识点二 图像变换
思考 y=x2和y=2(x+1)2+3的图像之间有什么关系?
答案 y=x2的图像各点纵坐标变为原来的2倍,可得y=2x2的图像;再把y=2x2的图像向左平移1个单位长度,再上平移3个单位长度,得y=2(x+1)2+3的图像.
梳理 由y=x2的图像各点纵坐标变为原来的a倍,左移个单位长度,上移个单位长度,可得y=a2+的图像,即y=ax2+bx+c的图像.
知识点三 二次函数的三种形式
思考 我们知道y=x2-2x=(x-1)2-1=(x-2)x,那么点(1,-1),数0,2是y=x2-2x的什么?
答案 点(1,-1)是y=x2-2x的顶点,数0,2是方程x2-2x=0的两根.
梳理 (1)二次函数的一般式y=ax2+bx+c(a≠0).
(2)如果已知二次函数的顶点坐标为(-h,k),则可将二次函数设为y=a(x+h)2+k.
(3)如果已知方程ax2+bx+c=0的两根x1,x2(即抛物线与x轴交点横坐标),可设为y=a(x-x1)(x-x2).
知识点四 二次函数的性质
函数
二次函数y=ax2+bx+c=a2+(a,b,c是常数,且a≠0)
图像
性质
开口
向上
向下
对称轴方程
x=-
x=-
顶点坐标
单调性
在区间上是减函数,在区间上是增函数
在区间上是增函数,在区间上是减函数
最值
当x=-时,y有最小值,ymin=
当x=-时,y有最大值,ymax=
1.若函数f(x)=(a-1)x+b在R上为增函数,则a>1,b∈R.( √ )
2.若函数y=x2的图像向上平移1个单位长度,则所得图像对应的函数解析式为y=(x+1)2.
( × )
3.二次函数y=x2与y=3x2的图像的形状相同.( × )
类型一 二次函数解析式的求解
例1 已知二次函数y=ax2+bx+c(a≠0)的图像与x轴相交于点A(-3,0),对称轴为x=-1,顶点M到x轴的距离为2,求此函数的解析式.
考点 二次函数解析式求法
题点 一般式求法
解 方法一 代入A(-3,0),
有9a-3b+c=0,①
由对称轴为x=-1,得-=-1,②
顶点M到x轴的距离为|a-b+c-0|=2,③
联立①②③解得或
所以此函数的解析式为y=x2+x-或y=-x2-x+.
考点 二次函数解析式求法
题点 顶点式求法
方法二 因为二次函数图像的对称轴是x=-1,
又顶点M到x轴的距离为2,所以顶点的坐标为(-1,2)或(-1,-2),
故可得二次函数的解析式为y=a(x+1)2+2或y=a(x+1)2-2.
因为图像过点A(-3,0),所以0=a(-3+1)2+2或0=a(-3+1)2-2,解得a=-或a=.
故所求二次函数的解析式为y=-(x+1)2+2=-x2-x+或y=(x+1)2-2=x2+x-.
考点 二次函数解析式的求法
题点 两根式求法
方法三 因为二次函数图像的对称轴为x=-1,
又图像过点A(-3,0),所以点A关于对称轴的对称点A′(1,0)也在图像上,
所以可得二次函数的解析式为y=a(x+3)(x-1).
由题意得顶点坐标为(-1,2)或(-1,-2),
分别代入上式,解得a=-或a=.
故所求二次函数的解析式为y=-(x+3)(x-1)=-x2-x+或y=(x+3)(x-1)=x2+x-.
反思与感悟 求二次函数解析式的步骤
跟踪训练1 (1)y=ax2+6x-8与直线y=-3x交于点A(1,m),求a.
考点 二次函数解析式的求法
题点 一般式求法
解 把A(1,m)代入y=-3x,得m=-3,
把(1,-3)代入y=ax2+6x-8,得
a+6-8=-3,即a=-1.
(2)f(x)=x2+bx+c,若f(-4)=f(0),f(-2)=-2,求f(x).
考点 二次函数解析式求法
题点 顶点式求法
解 方法一 由f(-4)=f(0),知f(x)的对称轴为
x==-2,
又f(-2)=-2,∴顶点坐标为(-2,-2),
∴f(x)=(x+2)2-2=x2+4x+2.
考点 二次函数解析式的求法
题点 两根式求法
方法二 由f(-4)=f(0),可设f(x)=x(x+4)+c.
代入x=-2,得-2×(-2+4)+c=-2,∴c=2.
∴f(x)=x2+4x+2.
类型二 二次函数的图像及变换
例2 由函数y=x2的图像如何得到f(x)=-x2+2x+3的图像.
考点 二次函数图像
题点 二次函数图像变换
解 f(x)=-x2+2x+3=-(x2-2x)+3
=-(x2-2x+1-1)+3=-(x-1)2+4,
∴由y=-x2的图象与y=x2的图像关于x轴对称,
可得y=-x2的图像.
由y=-x2的图像向右平移1个单位长度,向上平移4个单位长度,可得y=-(x-1)2+4,即y=-x2+2x+3的图像.
引申探究
利用f(x)=-x2+2x+3的图像比较f(-1),f(2)的大小.
解 f(x)图像如图.
由图知越接近对称轴,函数值越大.
由|-1-1|=2>|2-1|=1,
即f(2)比f(-1)更接近对称轴,∴f(2)>f(-1).
反思与感悟 处理二次函数y=ax2+bx+c(a≠0)的图像问题,主要是考虑其图像特征如开口、顶点、与x轴交点、与y轴交点、对称轴等与系数a,b,c之间的关系.
在图像变换中,记住“h正左移,h负右移,k正上移,k负下移”.
跟踪训练2 将二次函数f(x)=x2+bx+c的图像向左平移2个单位长度,再向上平移3个单位长度,得到二次函数f(x)=x2-2x+1的图像,则b=______,c=______.
考点 二次函数图像
题点 二次函数图像变换
答案 -6 6
解析 f(x)=x2-2x+1=(x-1)2,其图像顶点为(1,0).
将二次函数f(x)=x2-2x+1的图像向下平移3个单位长度,再向右平移2个单位长度后的图像的顶点为(3,-3),得到的抛物线为y=(x-3)2-3,即f(x)=x2+bx+c,
∴(x-3)2-3=x2+bx+c,即x2-6x+6=x2+bx+c,
∴b=-6,c=6.
类型三 二次函数的性质
例3 已知函数f(x)=x2-3x-:
(1)求函数图像的顶点坐标、对称轴方程和最值;
(2)若x∈[1,4],求函数值域.
考点 二次函数性质
题点 由解析式研究二次函数性质
解 (1)对函数右端的表达式配方,得
f(x)=(x-3)2-,
所以函数图像的顶点坐标为,
对称轴方程为x=3,最小值为-,无最大值.
(2)由于3∈[1,4],所以函数在区间[1,3]上是减函数,在区间[3,4]上是增函数,
所以当x=3时,ymin=-,
当x=1时,ymax=×4-=-,
所以函数的值域为.
反思与感悟 解析式、图像、性质三者各有特点又联系紧密,应用时在三者间灵活转化可使问题更易解决.
跟踪训练3 已知函数f(x)=ax2+2ax+1在区间[-1,2]上有最大值4,求实数a的值.
考点 二次函数性质
题点 由性质求参数范围
解 f(x)=a(x+1)2+1-a.
当a=0时,函数f(x)在区间[-1,2]上的值不变,恒为常数1,不符合题意,舍去;
当a>0时,函数f(x)在区间[-1,2]上是增函数,最大值为f(2)=8a+1=4,解得a=;
当a<0时,函数f(x)在区间[-1,2]上是减函数,最大值为f(-1)=1-a=4,解得a=-3.
综上,a的值为-3或.
1.二次函数f(x)=ax2+bx+c(a≠0)与g(x)=bx2+ax+c(b≠0)的图像可能是下图中的( )
考点 二次函数图像
题点 图像与a,b,c的关系
答案 D
解析 由于f(x),g(x)的图像的对称轴方程分别是x=-,x=-,则-与-同号,即f(x),g(x)的图像的对称轴位于y轴的同一侧,由此排除A,B;由C,D中给出的图像,可判定f(x),g(x)的图像的开口方向相反,故ab<0,于是->0,->0,即f(x),g(x)的图像的对称轴都位于y轴右侧,排除C,故选D.
2.设二次函数y=f(x)满足f(4+x)=f(4-x),又f(x)在[4,+∞)上是减函数,且f(a)≥f(0),则实数a的取值范围是( )
A.a≥4 B.0≤a≤8
C.a<0 D.a<0或a≥8
考点 二次函数性质
题点 二次函数性质综合应用
答案 B
解析 由题意知二次函数f(x)的图像关于直线x=4对称,则有f(0)=f(8).因为f(x)在[4,
+∞)上是减函数,所以f(x)在(-∞,4]上是增函数.当a∈(-∞,4]时,由f(a)≥f(0),得0≤a≤4;当a∈[4,+∞)时,由f(a)≥f(0),即f(a)≥f(8),得4≤a≤8.综上可知0≤a≤8.
3.已知f(x)=x2+bx+c,且f(-1)=f(3),则( )
A.f(1)>c>f(-1) B.f(1)
题点 二次函数的单调性
答案 B
解析 因为f(-1)=f(3),所以f(x)图像的对称轴为x=1,因此函数在区间(-∞,1]上是减函数,又c=f(0),所以f(1)
(1)图像过点(2,0),(4,0),(0,3);
(2)图像顶点为(1,2)并且过点(0,4);
(3)过点(1,1),(0,2),(3,5).
考点 二次函数解析式求法
题点 (1)两根式求法
(2)顶点式求法
(3)一般式求法
解 (1)由题意可设二次函数解析式为y=a(x-2)(x-4),
将(0,3)代入得a=.
∴所求二次函数解析式为y=(x-2)(x-4).
(2)由题意可设二次函数解析式为y=a(x-1)2+2,
将(0,4)代入得a=2,
∴所求二次函数解析式为y=2(x-1)2+2.
(3)由题意可设二次函数解析式为y=ax2+bx+c,
将(1,1),(0,2),(3,5)代入得
解得
∴所求二次函数解析式为y=x2-2x+2.
1.配方法是重要的数学方法,在处理二次函数图像变换,研究二次函数性质时使用频繁.
2.二次函数图像变换规律可以推广到一般函数,即:
(1)y=f(x)y=f(x+a);
(2)y=f(x)y=f(x)+b;
(3)y=f(x)y=af(x)(a>0);
(4)y=f(x)y=-f(x);
(5)y=f(x)y=f(-x).
一、选择题
1.函数f(x)=x2+mx+1的图像关于直线x=1对称,则( )
A.m=-2 B.m=2
C.m=-1 D.m=1
考点 二次函数解析式求法
题点 一般式求法
答案 A
解析 二次函数f(x)=x2+mx+1图像的对称轴为x=-,于是-=1,解得m=-2.
2.二次函数y=-x2+4x+t的顶点在x轴上,则t的值是( )
A.-4 B.4
C.-2 D.2
考点 二次函数解析式求法
题点 一般式求法
答案 A
解析 二次函数的图像开口向下,顶点在x轴上,所以对应一元二次方程的Δ=42-4×(-1)t=0,解得t=-4.
3.已知抛物线与x轴交于点(-1,0),(1,0),并且与y轴交于点(0,1),则抛物线的解析式为( )
A.y=-x2+1 B.y=x2+1
C.y=-x2-1 D.y=x2-1
考点 二次函数解析式求法
题点 两根式求法
答案 A
解析 设f(x)=a(x-1)(x+1),
代入(0,1),f(0)=a(0-1)(0+1)=-a=1,
∴a=-1,∴f(x)=1-x2.
4.若一次函数y=ax+b的图像经过第二、三、四象限,则二次函数y=ax2+bx的图像只可能是( )
考点 二次函数图像
题点 图像与a,b,c的关系
答案 C
解析 因为一次函数y=ax+b的图像经过第二、三、四象限,所以a<0,b<0,所以二次函数的图像开口向下,对称轴x=-<0,只有选项C满足.
5.若函数f(x)=x2+ax+b的图像与x轴的交点为(1,0)和(3,0),则函数f(x)( )
A.在(-∞,2]上是减少的,在[2,+∞)上是增加的
B.在(-∞,3)上是增加的
C.在[1,3]上是增加的
D.单调性不能确定
考点 二次函数性质
题点 二次函数单调性
答案 A
解析 由已知可得函数f(x)图像的对称轴为x=2,又二次项系数1>0,所以f(x)在(-∞,2]上是减少的,在[2,+∞)上是增加的.
6.函数y=-x2-2ax(0≤x≤1)的最大值是a2,则实数a的取值范围是( )
A.[0,1]B.[0,2]C.[-2,0]D.[-1,0]
考点 二次函数性质
题点 二次函数在闭区间上的最值
答案 D
解析 y=-(x+a)2+a2,要使ymax=a2,需满足0≤-a≤1,解得-1≤a≤0.
7.已知二次函数y=ax2+bx+c(a≠0)的图像顶点为(2,-1),与y轴交点坐标为(0,11),则( )
A.a=1,b=-4,c=-11
B.a=3,b=12,c=11
C.a=3,b=-6,c=-11
D.a=3,b=-12,c=11
考点 二次函数解析式求法
题点 一般式求法
答案 D
解析 由二次函数的图像与y轴交点坐标为(0,11),知c=11,又因为函数y=ax2+bx+c的图像顶点为(2,-1),所以-=2,=-1,解得a=3,b=-12.
二、填空题
8.函数y=3x2-x+2的图像向左平移1个单位长度,再向下平移2个单位长度,所得图像对应的函数解析式是________________.
考点 二次函数图像
题点 二次函数图像变换
答案 y=3x2+5x+2
解析 函数y=3x2-x+2的图像向左平移1个单位长度,得函数y=3(x+1)2-(x+1)+2的图像,再向下平移2个单位长度,得函数y=3(x+1)2-(x+1)+2-2的图像,即所得图像对应的函数解析式是y=3x2+5x+2.
9.如果函数f(x)=x2+2(a-1)x+2在区间(-∞,4]上是减少的,那么实数a的取值范围是________.
考点 二次函数性质
题点 二次函数单调性
答案 (-∞,-3]
解析 二次函数f(x)的图像开口向上,且对称轴方程为x=1-a,
所以f(x)的递减区间为(-∞,1-a],
故(-∞,4]?(-∞,1-a],因此1-a≥4,解得a≤-3.
10.设f(x)=x2+4x+3,不等式f(x)≥a对x∈R恒成立,则实数a的取值范围是________.
考点 二次函数性质
题点 二次函数最值
答案 (-∞,-1]
解析 f(x)≥a对x∈R恒成立?f(x)min≥a,
f(x)=(x+2)2-1,∴f(x)min=f(-2)=-1,
∴a≤-1.
三、解答题
11.已知二次函数f(x)的图像的对称轴是直线x=1,且f(1)=4,f(4)=-5.
(1)求函数f(x)的解析式,并画出f(x)的图像;
(2)根据图像写出函数f(x)的单调区间,并指明在该区间上的单调性;
(3)当函数f(x)在区间(-∞,m]上是增函数时,求实数m的取值范围.
考点 二次函数图像与性质
题点 图像性质综合应用
解 (1)设f(x)=ax2+bx+c(a≠0),由题意得
解得
所以函数f(x)=-x2+2x+3,f(x)的图像如图所示.
(2)由图像可得函数f(x)的单调区间是(-∞,1]和[1,+∞),其中函数f(x)在区间(-∞,1]上是增加的,在区间[1,+∞)上是减少的.
(3)由(2)知函数f(x)=-x2+2x+3在区间(-∞,1]上是增函数,那么(-∞,m]?(-∞,1],则有m≤1.
12.二次函数f(x)与g(x)的图像开口大小相同,开口方向也相同.已知函数g(x)的解析式和f(x)图像的顶点,写出函数f(x)的解析式.
(1)函数g(x)=x2,f(x)图像的顶点是(4,-7);
(2)函数g(x)=-2(x+1)2,f(x)图像的顶点是(-3,2).
考点 二次函数解析式求法
题点 顶点式求法
解 (1)因为f(x)与g(x)=x2的图像开口大小相同,开口方向也相同,
f(x)图像的顶点是(4,-7),
所以f(x)=(x-4)2-7=x2-8x+9.
(2)由题意知,f(x)的二次项系数为-2,
又因为f(x)图像的顶点是(-3,2),
所以f(x)=-2(x+3)2+2=-2x2-12x-16.
13.某商场以每件42元的价格购进一种服装,根据试营销量得知:这种服装每天的销售量t(t>0,t∈N)(件)与每件的销售价x(x>42,x∈N)(元)之间可看成是一次函数关系:t=-3x+204.
(1)写出商场每天卖这种服装的销售利润y(元)与每件的销售价x(元)之间的函数关系式(每天的销售利润是指所卖出服装的总销售所得与购进这些服装所花费金额的差);
(2)通过对所得函数关系式进行配方,指出:商场要想每天获得最大的销售利润,每件的销售价定为多少最为合适?最大销售利润为多少?
考点 二次函数性质
题点 二次函数最值
解 (1)由题意得,每天的销售利润y(元)与每件的销售价x(元)之间的函数关系式为y=(x-42)(-3x+204)=-3x2+330x-8568(42
四、探究与拓展
14.已知二次函数y=ax2+bx+c(a≠0)的图像如图所示,则下列结论中正确的是( )
A.a>0
B.当x>1时,y随x的增大而增大
C.c<0
D.3是方程ax2+bx+c=0的一个根
考点 二次函数图像
题点 二次函数图像与性质关系
答案 D
解析 从二次函数的图像可知,图像开口向下,a<0;当x>1时,y随x的增大而减小;当x=0时,y=c>0;二次函数图像的对称轴为直线x=1,函数图像与x轴的一个交点的横坐标为-1,则根据对称性,函数图像与x轴的另一个交点的横坐标为3.故选D.
15.已知函数f(x)=x2+2ax+3,x∈[-4,6].
(1)当a=-2时,求f(x)的最值;
(2)求实数a的取值范围,使y=f(x)在区间[-4,6]上是单调函数;
(3)当a=1时,求f(|x|)的单调区间.
考点 二次函数性质
题点 二次函数性质综合
解 (1)当a=-2时,f(x)=x2-4x+3=(x-2)2-1,
由于x∈[-4,6],∴f(x)在区间[-4,2]上是减少的,在区间[2,6]上是增加的,∴f(x)的最小值是f(2)=-1,
又f(-4)=35,f(6)=15,
∴f(x)的最大值是35.
(2)∵函数f(x)的图像开口向上,对称轴是x=-a,
∴要使f(x)在区间[-4,6]上是单调函数,
应有-a≤-4或-a≥6,即a≤-6或a≥4.
(3)当a=1时,f(x)=x2+2x+3,
∴f(|x|)=x2+2|x|+3,此时定义域为x∈[-6,6],
且f(x)=
∴f(|x|)的递增区间是(0,6],递减区间是[-6,0].
