第4章 1.2 利用二分法求方程的近似解
文档属性
| 名称 | 第4章 1.2 利用二分法求方程的近似解 |  | |
| 格式 | zip | ||
| 文件大小 | 236.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-21 08:48:30 | ||
图片预览




文档简介
1.2 利用二分法求方程的近似解
学习目标 1.理解二分法的原理及其适用条件.2.掌握二分法的实施步骤.3.体会二分法中蕴含的逐步逼近与程序化思想.
知识点一 二分法的原理
思考 通过上节课的学习,我们知道f(x)=lnx+2x-6的零点在区间(2,3)内,如何缩小零点所在区间(2,3)的范围?
答案 ①取区间(2,3)的中点2.5.
②计算f(2.5)的值,用计算器算得f(2.5)≈-0.084.因为f(2.5)·f(3)<0,所以零点在区间(2.5,3)内.
梳理 二分法的概念
如果在区间[a,b]上,函数f(x)的图像是一条连续的曲线,且f(a)·f(b)<0,则区间[a,b]内有方程f(x)=0的解.
依次取有解区间的中点,如果取到某个区间的中点x0,恰使f(x0)=0,则x0就是所求的一个解;如果区间中点的函数值总不等于零,那么,不断地重复上述操作,就得到一系列闭区间,方程的一个解在这些区间中,区间长度越来越小,端点逐步逼近方程的解,可以得到一个近似解.
像这样每次取区间的中点,将区间一分为二,再经比较,按需要留下其中一个小区间的方法称为二分法.
知识点二 精度与精确到
思考 “精确到0.1”与“精度为0.1”一样吗?
答案 不一样.比如得数是1.25或1.34,精确到0.1都是通过四舍五入后保留一位小数得1.3.而“精度为0.1”指零点近似值所在区间(a,b)满足|a-b|<0.1,比如零点近似值所在区间(1.25,1.34).若精度为0.1,则近似值可以是1.25,也可以是1.34.
梳理 在许多实际应用中,不需要求出方程精确的解,只要满足一定的精度就可以.设是方程f(x)=0的一个解,给定正数ε,若x0满足|x0-|<ε,就称x0是满足精度ε的近似解.
为了得到满足精度ε的近似解,只需找到方程的一个有解区间[a,b],使得区间长度b-a≤ε,那么区间(a,b)内任意一个数都是满足精度ε的近似解.
事实上,任意选取两数x1,x2∈(a,b),都有|x1-x2|<ε.由于∈(a,b),所以任意选取x′∈(a,b)都有|x′-|<ε.
知识点三 二分法求方程近似解的步骤
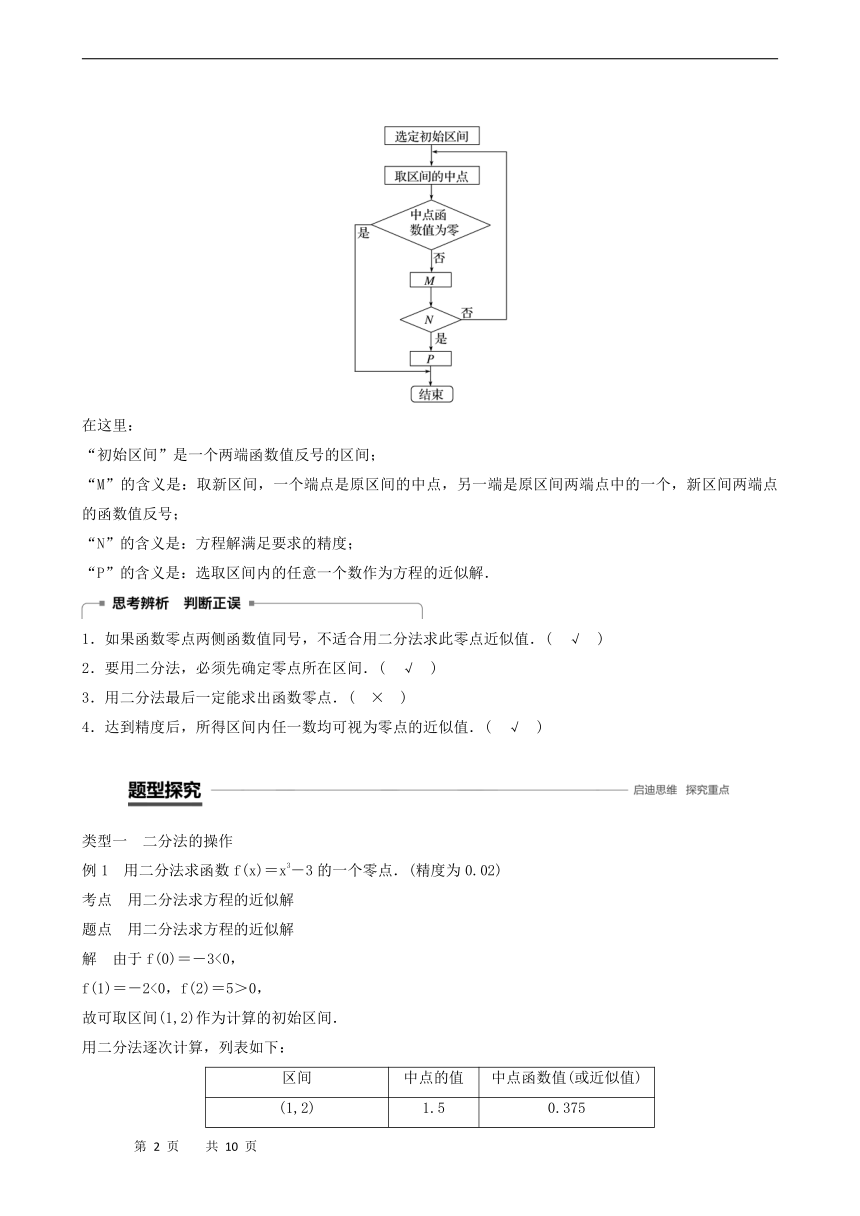
利用二分法求方程实数解的过程可以用下图表示出来.
在这里:
“初始区间”是一个两端函数值反号的区间;
“M”的含义是:取新区间,一个端点是原区间的中点,另一端是原区间两端点中的一个,新区间两端点的函数值反号;
“N”的含义是:方程解满足要求的精度;
“P”的含义是:选取区间内的任意一个数作为方程的近似解.
1.如果函数零点两侧函数值同号,不适合用二分法求此零点近似值.( √ )
2.要用二分法,必须先确定零点所在区间.( √ )
3.用二分法最后一定能求出函数零点.( × )
4.达到精度后,所得区间内任一数均可视为零点的近似值.( √ )
类型一 二分法的操作
例1 用二分法求函数f(x)=x3-3的一个零点.(精度为0.02)
考点 用二分法求方程的近似解
题点 用二分法求方程的近似解
解 由于f(0)=-3<0,
f(1)=-2<0,f(2)=5>0,
故可取区间(1,2)作为计算的初始区间.
用二分法逐次计算,列表如下:
区间
中点的值
中点函数值(或近似值)
(1,2)
1.5
0.375
(1,1.5)
1.25
-1.047
(1.25,1.5)
1.375
-0.400
(1.375,1.5)
1.4375
-0.030
(1.4375,1.5)
1.46875
0.168
(1.4375,1.46875)
1.453125
0.068
(1.4375,1.453125)
因为|1.453125-1.4375|=0.015625<0.02,
所以函数f(x)=x3-3的零点的近似值可取为1.4375.
引申探究
如何求的近似值?(精度为0.01)
解 设x=,则x3=2,即x3-2=0,
令f(x)=x3-2,则函数f(x)的零点的近似值就是的近似值,以下用二分法求其零点.
由f(1)=-1<0,f(2)=6>0,故可以取区间(1,2)为计算的初始区间.
用二分法逐次计算,列表如下:
区间
中点的值
中点函数值
(1,2)
1.5
1.375
(1,1.5)
1.25
-0.0469
(1.25,1.5)
1.375
0.5996
(1.25,1.375)
1.3125
0.2610
(1.25,1.3125)
1.28125
0.1033
(1.25,1.28125)
1.265625
0.0273
(1.25,1.265625)
1.2578125
-0.0100
由于|1.265625-1.2578125|=0.0078125<0.01,所以1.265625是函数的零点的近似值,即的近似值是1.265625.
反思与感悟 用二分法求函数零点的近似值关键有两点:一是初始区间的选取,符合条件(包括零点),又要使其长度尽量小;二是进行精度的判断,以决定是停止计算还是继续计算.
跟踪训练1 借助计算器或计算机用二分法求方程2x+3x=7的近似解.(精度为0.1)
考点 用二分法求方程的近似解
题点 用二分法求方程的近似解
解 原方程即2x+3x-7=0,令f(x)=2x+3x-7,
用计算器或计算机作出函数f(x)=2x+3x-7的对应值表与图像如下:
x
0
1
2
3
4
5
6
7
8
…
f(x)=2x+3x-7
-6
-2
3
10
21
40
75
142
273
…
观察图或表可知f(1)·f(2)<0,说明这个函数在区间(1,2)内有零点x0.
取区间(1,2)的中点x1=1.5,用计算器算得f(1.5)≈0.33.因为f(1)·f(1.5)<0,所以x0∈(1,1.5).
再取区间(1,1.5)的中点x2=1.25,用计算器算得f(1.25)≈-0.87.
因为f(1.25)·f(1.5)<0,所以x0∈(1.25,1.5).
同理可得,x0∈(1.375,1.5),x0∈(1.375,1.4375).
由于|1.375-1.4375|=0.0625<0.1,
所以原方程的近似解可取为1.4375.
类型二 二分法取中点的次数问题
例2 若函数f(x)在(1,2)内有1个零点,要使零点的近似值满足精度为0.01,则对区间(1,2)至少二等分( )
A.5次B.6次C.7次D.8次
考点 二分法的概念
题点 分析二分法计算的次数
答案 C
解析 设对区间(1,2)至少二等分n次,初始区间长为1.
第1次二等分后区间长为;
第2次二等分后区间长为;
第3次二等分后区间长为;
…;
第n次二等分后区间长为.
根据题意,得<0.01,∴n>log2100.
∵6故对区间(1,2)至少二等分7次.
反思与感悟 对于区间(a,b)二分一次区间长度为,二分二次区间长度为,…,二分n次区间长度为.令<ε,即2n>,nlg2>lg,n>,从而估算出至少要使用多少次二分法.
跟踪训练2 在用二分法求方程的近似解时,若初始区间的长度为1,精度为0.05,则取中点的次数不小于______.
考点 二分法的概念
题点 分析二分法计算的次数
答案 5
解析 ∵初始区间的长度为1,精度为0.05,
∴≤0.05,即2n≥20.又∵n∈N+,∴n≥5,
∴取中点的次数不小于5.
1.下列函数中,只能用二分法求其零点的是( )
A.y=x+7 B.y=5x-1
C.y=log3x D.y=x-x
考点 二分法的概念
题点 二分法概念的理解
答案 D
2.观察下列函数的图像,判断能用二分法求其零点的是( )
考点 二分法的概念
题点 判断是否能用二分法求解零点
答案 A
3.方程2x-1+x=5的根所在的区间为( )
A.(0,1) B.(1,2)
C.(2,3) D.(3,4)
考点 用二分法求方程的近似解
题点 用二分法判断函数零点所在区间
答案 C
4.定义在R上的函数f(x)的图像是连续不断的曲线,已知函数f(x)在区间(a,b)上有一个零点x0,且f(a)f(b)<0,用二分法求x0时,当f=0时,则函数f(x)的零点是( )
A.(a,b)外的点
B.x=
C.区间或内的任意一个实数
D.x=a或b
考点 用二分法求方程的近似解
题点 用二分法判断函数零点所在区间
答案 B
5.用二分法求函数y=f(x)在区间(2,4)上的唯一零点的近似值时,验证f(2)·f(4)<0,取区间(2,4)的中点x1==3,计算得f(2)·f(x1)<0,则此时零点x0所在的区间是( )
A.(2,4) B.(2,3)
C.(3,4) D.无法确定
考点 用二分法求方程的近似解
题点 用二分法判断函数零点所在区间
答案 B
1.二分就是平均分成两部分.二分法就是通过不断地将所选区间一分为二,使区间的两个端点逐步逼近零点,直至找到零点附近足够小的区间,根据所要求的精度,用此区间的某个数值近似地表示真正的零点.
2.二分法求方程近似解的适用范围:在包含方程解的一个区间上,函数图像是连续的,且两端点函数值反号.
3.求函数零点的近似值时,所要求的精度不同,得到的结果也不相同.
一、选择题
1.下列函数图像与x轴均有公共点,其中能用二分法求零点的是( )
考点 二分法的概念
题点 判断是否能用二分法求解零点
答案 C
解析 只有选项C中零点左右的函数值符号相反且函数图像连续,可以利用二分法求解.
2.用“二分法”可求近似解,对于精度ε说法正确的是( )
A.ε越大,零点的精度越高
B.ε越大,零点的精度越低
C.重复计算次数就是ε
D.重复计算次数与ε无关
考点 二分法的概念
题点 二分法概念的理解
答案 B
解析 依“二分法”的具体步骤可知,ε越大,零点的精度越低.
3.设f(x)=3x+3x-8,用二分法求方程3x+3x-8=0在x∈(1,2)内近似解的过程中得f(1)<0,f(1.5)>0,f(1.25)<0,则方程3x+3x-8=0的根落在区间( )
A.(1.25,1.5) B.(1,1.25)
C.(1.5,2) D.不能确定
考点 用二分法求方程的近似解
题点 用二分法判断函数零点所在区间
答案 A
解析 易知f(x)在R上是增函数.由题意可知f(1.25)·f(1.5)<0,故函数f(x)=3x+3x-8的零点落在区间(1.25,1.5)内.故选A.
4.用二分法求函数f(x)=lnx-的零点时,初始区间大致可选在( )
A.(1,2) B.(2,3) C.(3,4) D.(e,+∞)
考点 用二分法求方程的近似解
题点 用二分法判断函数零点所在区间
答案 B
解析 由于f(2)=ln2-1<0,f(3)=ln3->0,f(2)·f(3)<0,故初始区间可选(2,3).
5.函数f(x)=log3x-在区间[1,3]内有零点,则用二分法判断含有零点的区间为( )
A. B.
C. D.
考点 用二分法求函数的近似解
题点 用二分法判断函数零点所在的区间
答案 C
解析 f(1)=-<0,f(3)=>0,f(2)=log32-=log32-log33=log3=log3<0,f=log3-=log3-log33=log3>log3=log3>0,因此,函数f(x)的零点在区间内,故选C.
6.若函数f(x)=x3+x2-2x-2的一个正数零点附近的函数值用二分法逐次计算,参考数据如下表:
f(1)=-2
f(1.5)=0.625
f(1.25)=-0.984
f(1.375)=-0.260
f(1.438)=0.165
f(1.4065)=-0.052
那么方程x3+x2-2x-2=0的一个近似根(精度0.05)为( )
A.1.5B.1.375C.1.438D.1.25
考点 用二分法求方程的近似解
题点 用二分法求方程的近似解
答案 C
解析 ∵f(1.4065)<0,f(1.438)>0,
∴f(1.4065)·f(1.438)<0,
∴该方程的根在区间(1.4065,1.438),
又∵|1.4065-1.438|=0.0315<0.05,
∴方程的近似根为1.4065或1.438.故选C.
二、填空题
7.用二分法求函数f(x)在区间[a,b]内的零点时,需要的条件是________.
①f(x)在[a,b]上连续不断;②f(a)·f(b)<0;
③f(a)·f(b)>0;④f(a)·f(b)≥0.
考点 二分法的概念
题点 二分法概念的理解
答案 ①②
解析 由二分法适用条件直接可得.
8.用“二分法”求方程2x+log2x-4=0在区间(1,3)内的根,如果取区间的中点x0=2,那么下一个有根的区间是________.
考点 用二分法求方程的近似解
题点 用二分法判断函数零点所在区间
答案 (1,2)
解析 设f(x)=2x+log2x-4,因为f(1)·f(2)=(2+0-4)×(4+1-4)=-2<0,所以下一个有根的区间为(1,2).
9.若函数f(x)的图像是连续不断的,且f(0)>0,f(1)·f(2)·f(4)<0,则下列命题正确的是________.
①函数f(x)在区间(0,1)内有零点;
②函数f(x)在区间(1,2)内有零点;
③函数f(x)在区间(0,2)内有零点;
④函数f(x)在区间(0,4)内有零点.
考点 用二分法求方程的近似解
题点 用二分法判断函数零点所在区间
答案 ④
解析 ∵f(0)>0,而由f(1)·f(2)·f(4)<0,知f(1),f(2),f(4)中至少有一个小于0.∴函数f(x)在(0,4)上有零点.
10.设方程2x+2x=10的根为β,β所在区间为(n,n+1),则n=________.
考点 用二分法求方程的近似解
题点 用二分法判断函数零点所在区间
答案 2
解析 设f(x)=2x+2x-10,则f(x)在R上为增函数,
又f(0)=-9,f(1)=-6,f(2)=-2,f(3)=4,
∴f(2)·f(3)<0,∴β∈(2,3),∴n=2.
三、解答题
11.求函数f(x)=x2-5的近似解.(精度为0.1)
考点 用二分法求方程的近似解
题点 用二分法求方程的近似解
解 由于f(-2)=-1<0,
f(-3)=4>0,
故取区间(-3,-2)作为计算的初始区间,用二分法逐次计算,列表如下:
区间
中点的值
中点函数近似值
(-3,-2)
-2.5
1.25
(-2.5,-2)
-2.25
0.0625
(-2.25,-2)
-2.125
-0.4844
(-2.25,-2.125)
-2.1875
-0.2148
(-2.25,-2.1875)
-2.21875
-0.0771
由于|-2.25-(-2.1875)|=0.0625<0.1,
所以函数的一个近似解可取-2.25.
学习目标 1.理解二分法的原理及其适用条件.2.掌握二分法的实施步骤.3.体会二分法中蕴含的逐步逼近与程序化思想.
知识点一 二分法的原理
思考 通过上节课的学习,我们知道f(x)=lnx+2x-6的零点在区间(2,3)内,如何缩小零点所在区间(2,3)的范围?
答案 ①取区间(2,3)的中点2.5.
②计算f(2.5)的值,用计算器算得f(2.5)≈-0.084.因为f(2.5)·f(3)<0,所以零点在区间(2.5,3)内.
梳理 二分法的概念
如果在区间[a,b]上,函数f(x)的图像是一条连续的曲线,且f(a)·f(b)<0,则区间[a,b]内有方程f(x)=0的解.
依次取有解区间的中点,如果取到某个区间的中点x0,恰使f(x0)=0,则x0就是所求的一个解;如果区间中点的函数值总不等于零,那么,不断地重复上述操作,就得到一系列闭区间,方程的一个解在这些区间中,区间长度越来越小,端点逐步逼近方程的解,可以得到一个近似解.
像这样每次取区间的中点,将区间一分为二,再经比较,按需要留下其中一个小区间的方法称为二分法.
知识点二 精度与精确到
思考 “精确到0.1”与“精度为0.1”一样吗?
答案 不一样.比如得数是1.25或1.34,精确到0.1都是通过四舍五入后保留一位小数得1.3.而“精度为0.1”指零点近似值所在区间(a,b)满足|a-b|<0.1,比如零点近似值所在区间(1.25,1.34).若精度为0.1,则近似值可以是1.25,也可以是1.34.
梳理 在许多实际应用中,不需要求出方程精确的解,只要满足一定的精度就可以.设是方程f(x)=0的一个解,给定正数ε,若x0满足|x0-|<ε,就称x0是满足精度ε的近似解.
为了得到满足精度ε的近似解,只需找到方程的一个有解区间[a,b],使得区间长度b-a≤ε,那么区间(a,b)内任意一个数都是满足精度ε的近似解.
事实上,任意选取两数x1,x2∈(a,b),都有|x1-x2|<ε.由于∈(a,b),所以任意选取x′∈(a,b)都有|x′-|<ε.
知识点三 二分法求方程近似解的步骤
利用二分法求方程实数解的过程可以用下图表示出来.
在这里:
“初始区间”是一个两端函数值反号的区间;
“M”的含义是:取新区间,一个端点是原区间的中点,另一端是原区间两端点中的一个,新区间两端点的函数值反号;
“N”的含义是:方程解满足要求的精度;
“P”的含义是:选取区间内的任意一个数作为方程的近似解.
1.如果函数零点两侧函数值同号,不适合用二分法求此零点近似值.( √ )
2.要用二分法,必须先确定零点所在区间.( √ )
3.用二分法最后一定能求出函数零点.( × )
4.达到精度后,所得区间内任一数均可视为零点的近似值.( √ )
类型一 二分法的操作
例1 用二分法求函数f(x)=x3-3的一个零点.(精度为0.02)
考点 用二分法求方程的近似解
题点 用二分法求方程的近似解
解 由于f(0)=-3<0,
f(1)=-2<0,f(2)=5>0,
故可取区间(1,2)作为计算的初始区间.
用二分法逐次计算,列表如下:
区间
中点的值
中点函数值(或近似值)
(1,2)
1.5
0.375
(1,1.5)
1.25
-1.047
(1.25,1.5)
1.375
-0.400
(1.375,1.5)
1.4375
-0.030
(1.4375,1.5)
1.46875
0.168
(1.4375,1.46875)
1.453125
0.068
(1.4375,1.453125)
因为|1.453125-1.4375|=0.015625<0.02,
所以函数f(x)=x3-3的零点的近似值可取为1.4375.
引申探究
如何求的近似值?(精度为0.01)
解 设x=,则x3=2,即x3-2=0,
令f(x)=x3-2,则函数f(x)的零点的近似值就是的近似值,以下用二分法求其零点.
由f(1)=-1<0,f(2)=6>0,故可以取区间(1,2)为计算的初始区间.
用二分法逐次计算,列表如下:
区间
中点的值
中点函数值
(1,2)
1.5
1.375
(1,1.5)
1.25
-0.0469
(1.25,1.5)
1.375
0.5996
(1.25,1.375)
1.3125
0.2610
(1.25,1.3125)
1.28125
0.1033
(1.25,1.28125)
1.265625
0.0273
(1.25,1.265625)
1.2578125
-0.0100
由于|1.265625-1.2578125|=0.0078125<0.01,所以1.265625是函数的零点的近似值,即的近似值是1.265625.
反思与感悟 用二分法求函数零点的近似值关键有两点:一是初始区间的选取,符合条件(包括零点),又要使其长度尽量小;二是进行精度的判断,以决定是停止计算还是继续计算.
跟踪训练1 借助计算器或计算机用二分法求方程2x+3x=7的近似解.(精度为0.1)
考点 用二分法求方程的近似解
题点 用二分法求方程的近似解
解 原方程即2x+3x-7=0,令f(x)=2x+3x-7,
用计算器或计算机作出函数f(x)=2x+3x-7的对应值表与图像如下:
x
0
1
2
3
4
5
6
7
8
…
f(x)=2x+3x-7
-6
-2
3
10
21
40
75
142
273
…
观察图或表可知f(1)·f(2)<0,说明这个函数在区间(1,2)内有零点x0.
取区间(1,2)的中点x1=1.5,用计算器算得f(1.5)≈0.33.因为f(1)·f(1.5)<0,所以x0∈(1,1.5).
再取区间(1,1.5)的中点x2=1.25,用计算器算得f(1.25)≈-0.87.
因为f(1.25)·f(1.5)<0,所以x0∈(1.25,1.5).
同理可得,x0∈(1.375,1.5),x0∈(1.375,1.4375).
由于|1.375-1.4375|=0.0625<0.1,
所以原方程的近似解可取为1.4375.
类型二 二分法取中点的次数问题
例2 若函数f(x)在(1,2)内有1个零点,要使零点的近似值满足精度为0.01,则对区间(1,2)至少二等分( )
A.5次B.6次C.7次D.8次
考点 二分法的概念
题点 分析二分法计算的次数
答案 C
解析 设对区间(1,2)至少二等分n次,初始区间长为1.
第1次二等分后区间长为;
第2次二等分后区间长为;
第3次二等分后区间长为;
…;
第n次二等分后区间长为.
根据题意,得<0.01,∴n>log2100.
∵6
反思与感悟 对于区间(a,b)二分一次区间长度为,二分二次区间长度为,…,二分n次区间长度为.令<ε,即2n>,nlg2>lg,n>,从而估算出至少要使用多少次二分法.
跟踪训练2 在用二分法求方程的近似解时,若初始区间的长度为1,精度为0.05,则取中点的次数不小于______.
考点 二分法的概念
题点 分析二分法计算的次数
答案 5
解析 ∵初始区间的长度为1,精度为0.05,
∴≤0.05,即2n≥20.又∵n∈N+,∴n≥5,
∴取中点的次数不小于5.
1.下列函数中,只能用二分法求其零点的是( )
A.y=x+7 B.y=5x-1
C.y=log3x D.y=x-x
考点 二分法的概念
题点 二分法概念的理解
答案 D
2.观察下列函数的图像,判断能用二分法求其零点的是( )
考点 二分法的概念
题点 判断是否能用二分法求解零点
答案 A
3.方程2x-1+x=5的根所在的区间为( )
A.(0,1) B.(1,2)
C.(2,3) D.(3,4)
考点 用二分法求方程的近似解
题点 用二分法判断函数零点所在区间
答案 C
4.定义在R上的函数f(x)的图像是连续不断的曲线,已知函数f(x)在区间(a,b)上有一个零点x0,且f(a)f(b)<0,用二分法求x0时,当f=0时,则函数f(x)的零点是( )
A.(a,b)外的点
B.x=
C.区间或内的任意一个实数
D.x=a或b
考点 用二分法求方程的近似解
题点 用二分法判断函数零点所在区间
答案 B
5.用二分法求函数y=f(x)在区间(2,4)上的唯一零点的近似值时,验证f(2)·f(4)<0,取区间(2,4)的中点x1==3,计算得f(2)·f(x1)<0,则此时零点x0所在的区间是( )
A.(2,4) B.(2,3)
C.(3,4) D.无法确定
考点 用二分法求方程的近似解
题点 用二分法判断函数零点所在区间
答案 B
1.二分就是平均分成两部分.二分法就是通过不断地将所选区间一分为二,使区间的两个端点逐步逼近零点,直至找到零点附近足够小的区间,根据所要求的精度,用此区间的某个数值近似地表示真正的零点.
2.二分法求方程近似解的适用范围:在包含方程解的一个区间上,函数图像是连续的,且两端点函数值反号.
3.求函数零点的近似值时,所要求的精度不同,得到的结果也不相同.
一、选择题
1.下列函数图像与x轴均有公共点,其中能用二分法求零点的是( )
考点 二分法的概念
题点 判断是否能用二分法求解零点
答案 C
解析 只有选项C中零点左右的函数值符号相反且函数图像连续,可以利用二分法求解.
2.用“二分法”可求近似解,对于精度ε说法正确的是( )
A.ε越大,零点的精度越高
B.ε越大,零点的精度越低
C.重复计算次数就是ε
D.重复计算次数与ε无关
考点 二分法的概念
题点 二分法概念的理解
答案 B
解析 依“二分法”的具体步骤可知,ε越大,零点的精度越低.
3.设f(x)=3x+3x-8,用二分法求方程3x+3x-8=0在x∈(1,2)内近似解的过程中得f(1)<0,f(1.5)>0,f(1.25)<0,则方程3x+3x-8=0的根落在区间( )
A.(1.25,1.5) B.(1,1.25)
C.(1.5,2) D.不能确定
考点 用二分法求方程的近似解
题点 用二分法判断函数零点所在区间
答案 A
解析 易知f(x)在R上是增函数.由题意可知f(1.25)·f(1.5)<0,故函数f(x)=3x+3x-8的零点落在区间(1.25,1.5)内.故选A.
4.用二分法求函数f(x)=lnx-的零点时,初始区间大致可选在( )
A.(1,2) B.(2,3) C.(3,4) D.(e,+∞)
考点 用二分法求方程的近似解
题点 用二分法判断函数零点所在区间
答案 B
解析 由于f(2)=ln2-1<0,f(3)=ln3->0,f(2)·f(3)<0,故初始区间可选(2,3).
5.函数f(x)=log3x-在区间[1,3]内有零点,则用二分法判断含有零点的区间为( )
A. B.
C. D.
考点 用二分法求函数的近似解
题点 用二分法判断函数零点所在的区间
答案 C
解析 f(1)=-<0,f(3)=>0,f(2)=log32-=log32-log33=log3=log3<0,f=log3-=log3-log33=log3>log3=log3>0,因此,函数f(x)的零点在区间内,故选C.
6.若函数f(x)=x3+x2-2x-2的一个正数零点附近的函数值用二分法逐次计算,参考数据如下表:
f(1)=-2
f(1.5)=0.625
f(1.25)=-0.984
f(1.375)=-0.260
f(1.438)=0.165
f(1.4065)=-0.052
那么方程x3+x2-2x-2=0的一个近似根(精度0.05)为( )
A.1.5B.1.375C.1.438D.1.25
考点 用二分法求方程的近似解
题点 用二分法求方程的近似解
答案 C
解析 ∵f(1.4065)<0,f(1.438)>0,
∴f(1.4065)·f(1.438)<0,
∴该方程的根在区间(1.4065,1.438),
又∵|1.4065-1.438|=0.0315<0.05,
∴方程的近似根为1.4065或1.438.故选C.
二、填空题
7.用二分法求函数f(x)在区间[a,b]内的零点时,需要的条件是________.
①f(x)在[a,b]上连续不断;②f(a)·f(b)<0;
③f(a)·f(b)>0;④f(a)·f(b)≥0.
考点 二分法的概念
题点 二分法概念的理解
答案 ①②
解析 由二分法适用条件直接可得.
8.用“二分法”求方程2x+log2x-4=0在区间(1,3)内的根,如果取区间的中点x0=2,那么下一个有根的区间是________.
考点 用二分法求方程的近似解
题点 用二分法判断函数零点所在区间
答案 (1,2)
解析 设f(x)=2x+log2x-4,因为f(1)·f(2)=(2+0-4)×(4+1-4)=-2<0,所以下一个有根的区间为(1,2).
9.若函数f(x)的图像是连续不断的,且f(0)>0,f(1)·f(2)·f(4)<0,则下列命题正确的是________.
①函数f(x)在区间(0,1)内有零点;
②函数f(x)在区间(1,2)内有零点;
③函数f(x)在区间(0,2)内有零点;
④函数f(x)在区间(0,4)内有零点.
考点 用二分法求方程的近似解
题点 用二分法判断函数零点所在区间
答案 ④
解析 ∵f(0)>0,而由f(1)·f(2)·f(4)<0,知f(1),f(2),f(4)中至少有一个小于0.∴函数f(x)在(0,4)上有零点.
10.设方程2x+2x=10的根为β,β所在区间为(n,n+1),则n=________.
考点 用二分法求方程的近似解
题点 用二分法判断函数零点所在区间
答案 2
解析 设f(x)=2x+2x-10,则f(x)在R上为增函数,
又f(0)=-9,f(1)=-6,f(2)=-2,f(3)=4,
∴f(2)·f(3)<0,∴β∈(2,3),∴n=2.
三、解答题
11.求函数f(x)=x2-5的近似解.(精度为0.1)
考点 用二分法求方程的近似解
题点 用二分法求方程的近似解
解 由于f(-2)=-1<0,
f(-3)=4>0,
故取区间(-3,-2)作为计算的初始区间,用二分法逐次计算,列表如下:
区间
中点的值
中点函数近似值
(-3,-2)
-2.5
1.25
(-2.5,-2)
-2.25
0.0625
(-2.25,-2)
-2.125
-0.4844
(-2.25,-2.125)
-2.1875
-0.2148
(-2.25,-2.1875)
-2.21875
-0.0771
由于|-2.25-(-2.1875)|=0.0625<0.1,
所以函数的一个近似解可取-2.25.
