北师大版初中数学八年级上册知识讲解,巩固练习(教学资料,补习资料):第30讲《平行线的证明》全章复习与巩固(基础)含解析
文档属性
| 名称 | 北师大版初中数学八年级上册知识讲解,巩固练习(教学资料,补习资料):第30讲《平行线的证明》全章复习与巩固(基础)含解析 |

|
|
| 格式 | zip | ||
| 文件大小 | 298.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-20 00:00:00 | ||
图片预览




文档简介
《平行线的证明》全章复习与巩固(提高)知识讲解
【学习目标】
了解定义及命题的概念与构成,并能通过证明或举反例判定命题的真假;
2. 区别平行线的判定与性质,并能灵活运用;
3. 理解并能灵活运用三角形的内角和定理及其推论.
【知识网络】
【要点梳理】
要点一、定义、命题及证明
1.定义:一般地,用来说明一个名词或者一个术语的意义的句子叫做定义.
2.命题:判断一件事情的句子,叫做命题. 要点诠释:
(1)命题一般由条件和结论组成. (2)正确的命题称为真命题,不正确的命题称为假命题. (3)公认的真命题叫做公理.
(4) 经过证明的真命题称为定理.
3.证明: 除了公理外,其它的真命题的正确性都要通过推理的方法进行证实,这种演绎推理的过程叫做证明. 要点诠释:实验、观察、操作所得出的结论不一定都正确,必须推理论证后才能得出正确的结论.
要点二、平行线的判定与性质
1.平行线的判定
判定方法1:同位角相等,两直线平行.
判定方法2:内错角相等,两直线平行.
判定方法3:同旁内角互补,两直线平行.
要点诠释:根据平行线的定义和平行公理的推论,平行线的判定方法还有:
(1)平行线的定义:在同一平面内,如果两条直线没有交点(不相交),那么两直线平行.
(2)如果两条直线都平行于第三条直线,那么这两条直线平行(平行线的传递性).
(3)在同一平面内,垂直于同一直线的两条直线平行.
(4)平行公理:经过直线外一点,有且只有一条直线与这条直线平行.
2.平行线的性质
性质1:两直线平行,同位角相等;
性质2:两直线平行,内错角相等;
性质3:两直线平行,同旁内角互补.
要点诠释:根据平行线的定义和平行公理的推论,平行线的性质还有:
(1)若两条直线平行,则这两条直线在同一平面内,且没有公共点.
(2)如果一条直线与两条平行线中的一条直线垂直,那么它必与另一条直线垂直.
要点三、三角形的内角和定理及推论
三角形的内角和定理:三角形的内角和等于180°.
推论:(1)三角形的一个外角等于和它不相邻的两个内角的和.
(2)三角形的一个外角大于任何一个和它不相邻的内角.
要点诠释:
(1)由一个公理或定理直接推出的真命题,叫做这个公理或定理的推论.
(2)推论可以当做定理使用.
【典型例题】
类型一、定义、命题及证明
1. 我们知道任何一个命题都由条件和结论两部分组成,如果我们把一个命题的条件变结论,结论变条件,那么所得的是不是一个命题?试举例说明.
【答案与解析】
解:是一个命题,例如“对顶角相等”条件结论互换就变为“相等的角是对顶角”.
【总结升华】如果将一个命题的条件与结论互换,则得到这个命题的逆命题,但原命题正确,逆命题不一定正确.
举一反三:
【变式】下列命题中,真命题有( ) .
若x=a,则x2-(a+b)x+ab=0
直线外一点到这条直线的垂线段,叫做这个点到这条直线的距离
如果 =0,那么x=±2
如果a=b,那么a3=b3
A.1个 B.2个 C.3个 D.4个
【答案】C
2.如图所示,O是直线AB上一点,射线OC、OD在AB的两侧,且∠AOC=∠BOD,试证明∠AOC与∠BOD是对顶角.
【答案】
证明:因为∠AOC+∠COB=180°(平角定义),
又因为∠AOC=∠BOD(已知),
所以∠BOD+∠COB=180°,即∠COD=180°.
所以C、O、D三点在一条直线上(平角定义),
即直线AB、CD相交于点O,
所以∠AOC与∠BOD是对顶角(对顶角定义).
【总结升华】证三点共线的方法,通常采用证这三点组成的角为平角,即∠COD=180°.
类型二、平行线的性质与判定
3. (2019春?胶州市期中)将一副三角板中的两根直角顶点C叠放在一起(如图①),其中∠A=30°,∠B=60°,∠D=∠E=45°.
(1)若∠BCD=150°,求∠ACE的度数;
(2)试猜想∠BCD与∠ACE的数量关系,请说明理由;
(3)若按住三角板ABC不动,绕顶点C转动三角板DCE,试探究∠BCD等于多少度时,CD∥AB,并简要说明理由.
【思路点拨】(1)由∠BCD=150°,∠ACB=90°,可得出∠DCA的度数,进而得出∠ACE的度数;
(2)根据(1)中的结论可提出猜想,再由∠BCD=∠ACB+∠ACD,∠ACE=∠DCE﹣∠ACD可得出结论;
(3)根据平行线的判定定理,画出图形即可求解.
【答案与解析】解:(1)∵∠BCA=∠ECD=90°,∠BCD=150°,
∴∠DCA=∠BCD﹣∠BCA=150°﹣90°=60°,
∴∠ACE=∠ECD﹣∠DCA=90°﹣60°=30°;
(2)∠BCD+∠ACE=180°,理由如下:
∵∠BCD=∠ACB+∠ACD=90°+∠ACD,
∠ACE=∠DCE﹣∠ACD=90°﹣∠ACD,
∴∠BCD+∠ACE=180°;
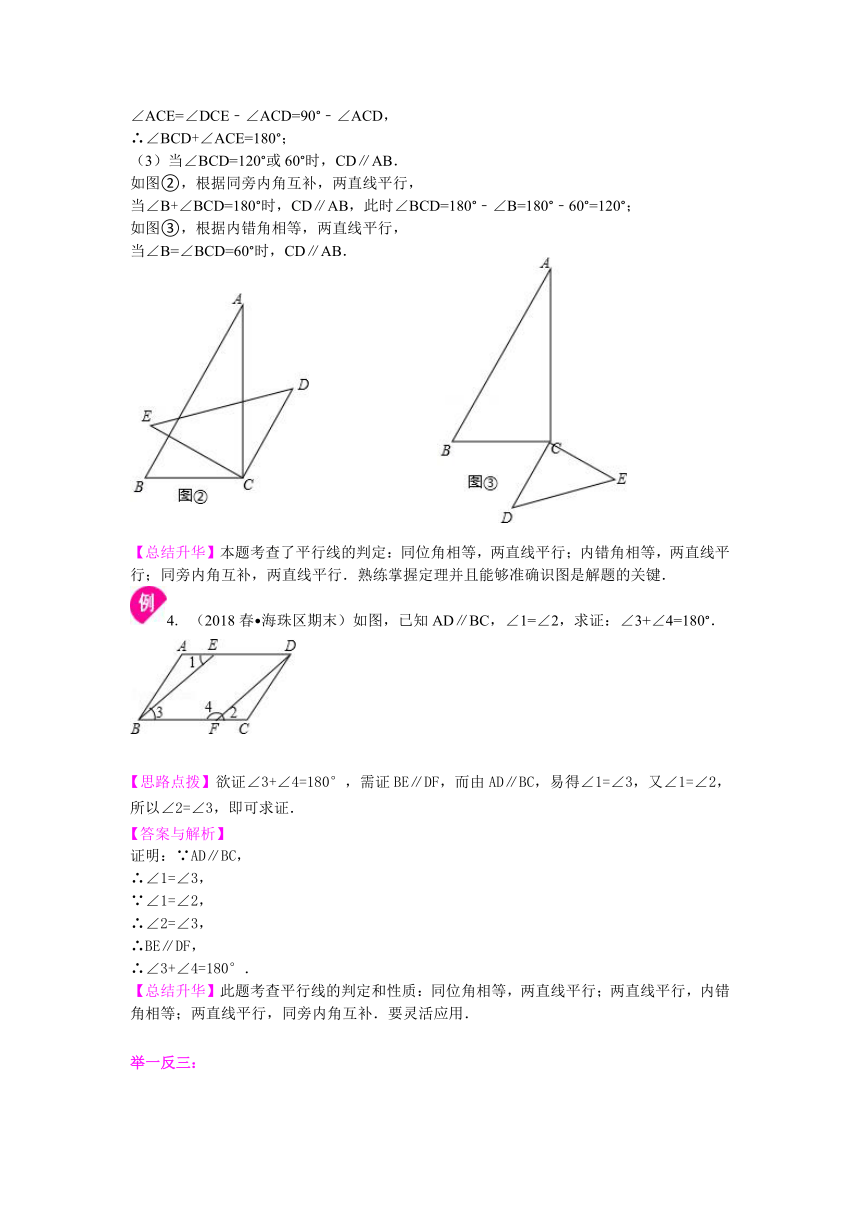
(3)当∠BCD=120°或60°时,CD∥AB.
如图②,根据同旁内角互补,两直线平行,
当∠B+∠BCD=180°时,CD∥AB,此时∠BCD=180°﹣∠B=180°﹣60°=120°;
如图③,根据内错角相等,两直线平行,
当∠B=∠BCD=60°时,CD∥AB.
【总结升华】本题考查了平行线的判定:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.熟练掌握定理并且能够准确识图是解题的关键.
4. (2018春?海珠区期末)如图,已知AD∥BC,∠1=∠2,求证:∠3+∠4=180°.
【思路点拨】欲证∠3+∠4=180°,需证BE∥DF,而由AD∥BC,易得∠1=∠3,又∠1=∠2,所以∠2=∠3,即可求证.
【答案与解析】
证明:∵AD∥BC,
∴∠1=∠3,
∵∠1=∠2,
∴∠2=∠3,
∴BE∥DF,
∴∠3+∠4=180°.
【总结升华】此题考查平行线的判定和性质:同位角相等,两直线平行;两直线平行,内错角相等;两直线平行,同旁内角互补.要灵活应用.
举一反三:
【变式1】(2018春?大名)如图:AD∥BC,∠DAC=60°,∠ACF=25°,∠EFC=145°,则直线EF与BC的位置关系是 .
【答案】
解:平行.
∵AD∥BC,
∴∠ACB=∠DAC=60°,
∵∠ACF=25°,
∴∠FCB=35°,
∴∠EFC+∠FCB=145°+35°=180°,
∴EF∥BC,故答案为:平行.
【变式2】已知:如图,∠ABC=∠ADC,BF、DE分别平分∠ABC与∠ADC,且∠1=∠3.
求证:AB∥DC.
【答案】
证明:∵∠ABC=∠ADC,
∴(等式性质).
又∵BF、DE分别平分∠ABC与∠ADC,
∴∠1=,∠2=(角平分线的定义).
∴∠1=∠2 (等量代换).
又∵∠1=∠3(已知),
∴∠2=∠3(等量代换).
∴AB∥DC(内错角相等,两直线平行).
类型三、三角形的内角和定理及推论
5.如图,P是△ABC 内一点,请用量角器量出∠ABP.∠ACP.∠A和∠BPC的大小,再计算一下,∠ABP+∠ACP+∠A是多少度?这三个角的和与∠BPC有什么关系?你能用学到的知识来解释其中的道理吗?你能判断∠BPC和∠A的大小吗?
【答案与解析】
解:∠ABP+∠ACP+∠A=∠BPC,∠BPC>∠A。
证明:如下图,延长BP到D,
则∠PDC=∠A+∠∠ABP,∠PDC>∠A.
同理,∠BPC=∠PDC+∠ACP,∠BPC>∠PDC.
所以∠BPC=∠ABP+∠ACP+∠A ,∠BPC>∠A .
举一反三:
【变式1】如图,△ABC的两外角平分线交于点P,易证∠P=90°-∠A;△ABC两内角的平分线交于点Q,易证∠BQC=90°+∠A;那么△ABC的内角平分线BM与外角平分CM的夹角
∠M=_____∠A.
【答案】
【变式2】如图,E是BC延长线上的点,∠1=∠2.求证:∠BAC>∠B.
【答案】
证明:∵∠2=∠B+∠D
∴∠B=∠2-∠D
又∵∠BAC=∠1+∠D ∠1=∠2
∴∠BAC>∠B
类型四、实际应用
6.手工制作课上,老师先将一张长方形纸片折叠成如图所示的那样,若折痕与一条边BC的夹角∠EFB=30°,你能说出∠EGF的度数吗?
【思路点拨】长方形的对边是平行的,所以AD∥BC,可得∠DEF=∠EFG=30°,又因为折后重合部分相等,所以∠GEF=∠DEF=30°,所以∠DEG=2∠DEF=60°,又因为两直线平行,同旁内角互补,所以∠EGC=180°-∠DEG,问题可解.
【答案与解析】
解:因为AD∥BC(已知),
所以∠DEF=∠EFG=30°(两直线平行,内错角相等).
因为∠GEF=∠DEF=30°(对折后重合部分相等),
所以∠DEG=2∠DEF=60°.
所以∠EGC=180°-∠DEG=180°-60°=120°(两直线平行,同旁内角互补).
【总结升华】本题利用了:(1)折叠的性质:折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等;(2)平行线的性质.
【巩固练习】
一、选择题
1.下列命题中,真命题是( ).
A.任何数的绝对值都是正数 B.任何数的零次幂都等于1
C.互为倒数的两个数的和为零D.在数轴上表示的两个数,右边的数比左边的数大
2.一学员在广场上练习驾驶汽车,两次拐弯后行驶的方向与原来的方向相同,这两次拐弯的角度可能是( ) .
A.第一次向左拐30°,第二次向右拐30°
B.第一次向右拐50°,第二次向左拐130°
C.第一次向左拐50°,第二次向左拐130°
D.第一次向左拐50°,第二次向右拐130°
3.(2018春?通川区期末)如图,如果∠1=∠2,DE∥BC,则下列结论正确的个数为( )
(1)FG∥DC;(2)∠AED=∠ACB;(3)CD平分∠ACB;(4)∠1+∠B=90°;
(5)∠BFG=∠BDC.
A.1个 B.2个 C.3个 D.4个
4.两条平行直线被第三条直线所截时,产生的八个角中,角平分线互相平行的两个角是( ). A.同位角 B.同旁内角 C.内错角 D. 同位角或内错角
5.(2019?南湖区一模)如图,将△ABC沿DE,EF翻折,顶点A,B均落在点O处,且EA与EB重合于线段EO,若∠CDO+∠CFO=98°,则∠C的度数为( )
A.40° B.41° C.42° D.43°
6. 如图,已知∠A=∠C,如果要判断AB∥CD,则需要补充的条件是( ).
A.∠ABD=∠CEF B.∠CED=∠ADB
C.∠CDB=∠CEF D.∠ABD+∠CED=180°
7.如图,,则AEB=( ).
A. B. C. D.
8. 把一张对面互相平行的纸条折成如图所示,EF是折痕,若∠EFB=32°,则下列结论不正确的有( ).
A. B. ∠AEC=148° C. ∠BGE=64° D. ∠BFD=116°
二、填空题
9.(荆州二模)如图所示,AB∥CD,点E在CB的延长线上.若∠ECD=110°,则∠ABE的度数为________.
10.如图,l∥m,∠1=115°,∠2=95°,则∠3= .
11.如图所示,AB∥CD,MN交AB、CD于E、F,EG和FG分别是∠BEN和∠MFD的平分线,那么EG与FG的位置关系是 .
12.(2019春?南陵县期中)如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠1=30°,∠2=20°,则∠B= .
13.(2018春?苏州)如图所示,∠A=10°,∠ABC=90°,∠ACB=∠DCE,∠ADE=∠EDF,∠CED=∠FEG.则∠F= .
14. 我们已经证明了“三角形的内角等于180°”,易证“四边形的内角和等于360°=2×180°,五边形的内角和等于540°=3×180°,……”试猜想十边形的内角和等于
度.
15. 五角形的五个内角的和是________.
16. 如图,下面四个条件:(1),(2),(3),(4),
请你以其中两个论断为条件,一个论断为结论,组成一个真命题:如果 ,那么 .(只填序号即可)
三、解答题
17.如图所示,在平行四边形ABCD中,AQ,BN,CN,DQ分别是∠DAB,∠ABC,∠BCD,
∠CDA的平分线,AQ与BN交于P,CN与DQ交于M,在不添加其他条件的情况下,试写出一个由上述条件推出的结论,并给出证明过程.(推理过程中用到“平行四边形”和“角平分线”这两个条件)
18. 如图所示,已知∠1=50°,∠2=130°,∠4=50°,∠6=130°,试说明a∥b,b∥c,d∥e,a∥c.
19. 如图所示,已知AB∥CD,∠1=110°,∠2=125°,求∠x的大小.
20. (2018春?沛县期末)已知在四边形ABCD中,∠A=∠C=90°.
(1)∠ABC+∠ADC= ;
(2)如图1,若DE平分∠ABC的外角,BF平分∠ABC的外角,请写出DE与BF的位置关系,并证明.
(3)如图2,若BE、DE分别四等分∠ABC、∠ADC的外角(即∠CDE=∠CDN,∠CBE=∠CBM),试求∠E的度数.
【答案与解析】
一、选择题
1. 【答案】D;
2. 【答案】A;
【解析】首先根据题意对各选项画出示意图,观察图形,根据同位角相等,两直线平行,即可得出答案.
3. 【答案】C;
【解析】解:∵DE∥BC,∴∠DCB=∠1,∠AED=∠ACB,(2)正确;
∵∠1=∠2,∴∠2=∠DCB, ∴FG∥DC,(1)正确;∴∠BFG=∠BDC,(5)正确;
正确的个数有3个,故选:C.
4. 【答案】D;
【解析】三线八角中,角平分线互相平行的两角是同位角或内错角,互相垂直的两角是同旁内角.
5. 【答案】B;
【解析】解:如图,连接AO、BO.
由题意EA=EB=EO,
∴∠AOB=90°,∠OAB+∠OBA=90°,
∵DO=DA,FO=FB,
∴∠DAO=∠DOA,∠FOB=∠FBO,
∴∠CDO=2∠DAO,∠CFO=2∠FBO,
∵∠CDO+∠CFO=98°,
∴2∠DAO+2∠FBO=98°,
∴∠DAO+∠FBO=49°,
∴∠CAB+∠CBA=∠DAO+∠OAB+∠OBA+∠FBO=139°,
∴∠C=180°﹣(∠CAB+∠CBA)=180°﹣139°=41°,故选B.
6. 【答案】B;
7. 【答案】B;
【解析】∠EAB=75°-25°=50°.
8.【答案】B;
【解析】选项B中,∠AEC=180°-32°×2=116°,所以选项B错误.
二、填空题
9. 【答案】70°;
【解析】因AB∥CD,所以∠ABC=∠ECD=110°,所以∠ABE=180°-110°=70°.
10.【答案】150°;
【解析】∠1+∠2+∠3=360°,所以∠3=360°-(115°+95°)=150°.
11.【答案】垂直;
【解析】
解:EG⊥FG,理由如下:
∵ AB∥CD,∴ ∠BEN+∠MFD=180°.
∵ EG和FG分别是∠BEN和∠MFD的平分线,
∴ ∠GEN+∠GFM=(∠BEN+∠MFD)=×180°=90°.
∴ ∠EGF=180°-∠GEN-∠GFM=90°.
∴ EG⊥FG.
12.【答案】50°;
【解析】∵AE平分∠BAC,∴∠1=∠EAD+∠2,∴∠EAD=∠1﹣∠2=30°﹣20°=10°,
Rt△ABD中,∠B=90°﹣∠BAD=90°﹣30°﹣10°=50°.
13.【答案】70°;
14.【答案】1440°;
【解析】十边形的内角和:(10-2)×180°=1440°,
由此得n边形的内角和:(n-2)×180°.
15.【答案】180°;
【解析】如下图,∠A+∠C=∠2,∠B+∠D=∠1,而∠1+∠2+∠E=180°,从而得答案.
16.【答案】(2)(4),(1);(答案不唯一,只要答案合理即可)
【解析】通过证明全等可得答案.
三、解答题
17.【解析】
解:四边形PQMN为长方形. 在平行四边形ABCD中,∠ABC+∠BCD=180°, 又BN、CN分别平分∠ABC和∠BCD, ∴∠N=90°, 同理∠CMD=∠Q=∠APB=90°, 又∵∠CMD=∠NMQ,∠APB=∠NPQ, ∴四边形PQMN为长方形.
18.【解析】
解:因为∠1=50°,∠2=130°(已知),
所以∠1+∠2=180°.
所以a∥b(同旁内角互补,两直线平行).
所以∠3=∠1=50°(两直线平行,同位角相等).
又因为∠4=50°(已知),
所以∠3=∠4(等量代换).
所以d∥e(同位角相等,两直线平行).
因为∠5+∠6=180°(平角定义),∠6=130°(已知),
所以∠5=50°(等式的性质).
所以∠4=∠5(等量代换).
所以b∥c(内错角相等,两直线平行).
因为a∥b,b∥c(已知),
所以a∥c(平行于同一直线的两直线平行).
19.【解析】
解:过E点作EF∥AB,则∠3=180°-∠1=70°.
因为EF∥AB,AB∥CD,
所以EF∥CD.
所以∠4=180°-∠2=55°.
所以∠x=180°-∠3-∠4=55°.
20.【解析】
(1)解:∵∠A=∠C=90°,
∴∠ABC+∠ADC=360°﹣90°×2=180°;
故答案为:180°;
(2)解:延长DE交BF于G,
∵DE平分∠ADC,BF平分∠CBM,
∴∠CDE=∠ADC,∠CBF=∠CBM,
又∵∠CBM=180°﹣∠ABC=180°﹣(180°﹣∠ADC)=∠ADC,
∴∠CDE=∠CBF,
又∵∠BED=∠CDE+∠C=∠CBF+∠BGE,
∴∠BGE=∠C=90°,
∴DG⊥BF,
即DE⊥BF;
(3)解:由(1)得:∠CDN+∠CBM=180°,
∵BE、DE分别四等分∠ABC、∠ADC的外角,
∴∠CDE+∠CBE=×180°45°,
延长DC交BE于H,
由三角形的外角性质得,∠BHD=∠CDE+∠E,∠BCD=∠BHD+∠CBE,
∴∠BCD=∠CBE+∠CDE+∠E,
∴∠E=90°﹣45°=45°.
【学习目标】
了解定义及命题的概念与构成,并能通过证明或举反例判定命题的真假;
2. 区别平行线的判定与性质,并能灵活运用;
3. 理解并能灵活运用三角形的内角和定理及其推论.
【知识网络】
【要点梳理】
要点一、定义、命题及证明
1.定义:一般地,用来说明一个名词或者一个术语的意义的句子叫做定义.
2.命题:判断一件事情的句子,叫做命题. 要点诠释:
(1)命题一般由条件和结论组成. (2)正确的命题称为真命题,不正确的命题称为假命题. (3)公认的真命题叫做公理.
(4) 经过证明的真命题称为定理.
3.证明: 除了公理外,其它的真命题的正确性都要通过推理的方法进行证实,这种演绎推理的过程叫做证明. 要点诠释:实验、观察、操作所得出的结论不一定都正确,必须推理论证后才能得出正确的结论.
要点二、平行线的判定与性质
1.平行线的判定
判定方法1:同位角相等,两直线平行.
判定方法2:内错角相等,两直线平行.
判定方法3:同旁内角互补,两直线平行.
要点诠释:根据平行线的定义和平行公理的推论,平行线的判定方法还有:
(1)平行线的定义:在同一平面内,如果两条直线没有交点(不相交),那么两直线平行.
(2)如果两条直线都平行于第三条直线,那么这两条直线平行(平行线的传递性).
(3)在同一平面内,垂直于同一直线的两条直线平行.
(4)平行公理:经过直线外一点,有且只有一条直线与这条直线平行.
2.平行线的性质
性质1:两直线平行,同位角相等;
性质2:两直线平行,内错角相等;
性质3:两直线平行,同旁内角互补.
要点诠释:根据平行线的定义和平行公理的推论,平行线的性质还有:
(1)若两条直线平行,则这两条直线在同一平面内,且没有公共点.
(2)如果一条直线与两条平行线中的一条直线垂直,那么它必与另一条直线垂直.
要点三、三角形的内角和定理及推论
三角形的内角和定理:三角形的内角和等于180°.
推论:(1)三角形的一个外角等于和它不相邻的两个内角的和.
(2)三角形的一个外角大于任何一个和它不相邻的内角.
要点诠释:
(1)由一个公理或定理直接推出的真命题,叫做这个公理或定理的推论.
(2)推论可以当做定理使用.
【典型例题】
类型一、定义、命题及证明
1. 我们知道任何一个命题都由条件和结论两部分组成,如果我们把一个命题的条件变结论,结论变条件,那么所得的是不是一个命题?试举例说明.
【答案与解析】
解:是一个命题,例如“对顶角相等”条件结论互换就变为“相等的角是对顶角”.
【总结升华】如果将一个命题的条件与结论互换,则得到这个命题的逆命题,但原命题正确,逆命题不一定正确.
举一反三:
【变式】下列命题中,真命题有( ) .
若x=a,则x2-(a+b)x+ab=0
直线外一点到这条直线的垂线段,叫做这个点到这条直线的距离
如果 =0,那么x=±2
如果a=b,那么a3=b3
A.1个 B.2个 C.3个 D.4个
【答案】C
2.如图所示,O是直线AB上一点,射线OC、OD在AB的两侧,且∠AOC=∠BOD,试证明∠AOC与∠BOD是对顶角.
【答案】
证明:因为∠AOC+∠COB=180°(平角定义),
又因为∠AOC=∠BOD(已知),
所以∠BOD+∠COB=180°,即∠COD=180°.
所以C、O、D三点在一条直线上(平角定义),
即直线AB、CD相交于点O,
所以∠AOC与∠BOD是对顶角(对顶角定义).
【总结升华】证三点共线的方法,通常采用证这三点组成的角为平角,即∠COD=180°.
类型二、平行线的性质与判定
3. (2019春?胶州市期中)将一副三角板中的两根直角顶点C叠放在一起(如图①),其中∠A=30°,∠B=60°,∠D=∠E=45°.
(1)若∠BCD=150°,求∠ACE的度数;
(2)试猜想∠BCD与∠ACE的数量关系,请说明理由;
(3)若按住三角板ABC不动,绕顶点C转动三角板DCE,试探究∠BCD等于多少度时,CD∥AB,并简要说明理由.
【思路点拨】(1)由∠BCD=150°,∠ACB=90°,可得出∠DCA的度数,进而得出∠ACE的度数;
(2)根据(1)中的结论可提出猜想,再由∠BCD=∠ACB+∠ACD,∠ACE=∠DCE﹣∠ACD可得出结论;
(3)根据平行线的判定定理,画出图形即可求解.
【答案与解析】解:(1)∵∠BCA=∠ECD=90°,∠BCD=150°,
∴∠DCA=∠BCD﹣∠BCA=150°﹣90°=60°,
∴∠ACE=∠ECD﹣∠DCA=90°﹣60°=30°;
(2)∠BCD+∠ACE=180°,理由如下:
∵∠BCD=∠ACB+∠ACD=90°+∠ACD,
∠ACE=∠DCE﹣∠ACD=90°﹣∠ACD,
∴∠BCD+∠ACE=180°;
(3)当∠BCD=120°或60°时,CD∥AB.
如图②,根据同旁内角互补,两直线平行,
当∠B+∠BCD=180°时,CD∥AB,此时∠BCD=180°﹣∠B=180°﹣60°=120°;
如图③,根据内错角相等,两直线平行,
当∠B=∠BCD=60°时,CD∥AB.
【总结升华】本题考查了平行线的判定:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.熟练掌握定理并且能够准确识图是解题的关键.
4. (2018春?海珠区期末)如图,已知AD∥BC,∠1=∠2,求证:∠3+∠4=180°.
【思路点拨】欲证∠3+∠4=180°,需证BE∥DF,而由AD∥BC,易得∠1=∠3,又∠1=∠2,所以∠2=∠3,即可求证.
【答案与解析】
证明:∵AD∥BC,
∴∠1=∠3,
∵∠1=∠2,
∴∠2=∠3,
∴BE∥DF,
∴∠3+∠4=180°.
【总结升华】此题考查平行线的判定和性质:同位角相等,两直线平行;两直线平行,内错角相等;两直线平行,同旁内角互补.要灵活应用.
举一反三:
【变式1】(2018春?大名)如图:AD∥BC,∠DAC=60°,∠ACF=25°,∠EFC=145°,则直线EF与BC的位置关系是 .
【答案】
解:平行.
∵AD∥BC,
∴∠ACB=∠DAC=60°,
∵∠ACF=25°,
∴∠FCB=35°,
∴∠EFC+∠FCB=145°+35°=180°,
∴EF∥BC,故答案为:平行.
【变式2】已知:如图,∠ABC=∠ADC,BF、DE分别平分∠ABC与∠ADC,且∠1=∠3.
求证:AB∥DC.
【答案】
证明:∵∠ABC=∠ADC,
∴(等式性质).
又∵BF、DE分别平分∠ABC与∠ADC,
∴∠1=,∠2=(角平分线的定义).
∴∠1=∠2 (等量代换).
又∵∠1=∠3(已知),
∴∠2=∠3(等量代换).
∴AB∥DC(内错角相等,两直线平行).
类型三、三角形的内角和定理及推论
5.如图,P是△ABC 内一点,请用量角器量出∠ABP.∠ACP.∠A和∠BPC的大小,再计算一下,∠ABP+∠ACP+∠A是多少度?这三个角的和与∠BPC有什么关系?你能用学到的知识来解释其中的道理吗?你能判断∠BPC和∠A的大小吗?
【答案与解析】
解:∠ABP+∠ACP+∠A=∠BPC,∠BPC>∠A。
证明:如下图,延长BP到D,
则∠PDC=∠A+∠∠ABP,∠PDC>∠A.
同理,∠BPC=∠PDC+∠ACP,∠BPC>∠PDC.
所以∠BPC=∠ABP+∠ACP+∠A ,∠BPC>∠A .
举一反三:
【变式1】如图,△ABC的两外角平分线交于点P,易证∠P=90°-∠A;△ABC两内角的平分线交于点Q,易证∠BQC=90°+∠A;那么△ABC的内角平分线BM与外角平分CM的夹角
∠M=_____∠A.
【答案】
【变式2】如图,E是BC延长线上的点,∠1=∠2.求证:∠BAC>∠B.
【答案】
证明:∵∠2=∠B+∠D
∴∠B=∠2-∠D
又∵∠BAC=∠1+∠D ∠1=∠2
∴∠BAC>∠B
类型四、实际应用
6.手工制作课上,老师先将一张长方形纸片折叠成如图所示的那样,若折痕与一条边BC的夹角∠EFB=30°,你能说出∠EGF的度数吗?
【思路点拨】长方形的对边是平行的,所以AD∥BC,可得∠DEF=∠EFG=30°,又因为折后重合部分相等,所以∠GEF=∠DEF=30°,所以∠DEG=2∠DEF=60°,又因为两直线平行,同旁内角互补,所以∠EGC=180°-∠DEG,问题可解.
【答案与解析】
解:因为AD∥BC(已知),
所以∠DEF=∠EFG=30°(两直线平行,内错角相等).
因为∠GEF=∠DEF=30°(对折后重合部分相等),
所以∠DEG=2∠DEF=60°.
所以∠EGC=180°-∠DEG=180°-60°=120°(两直线平行,同旁内角互补).
【总结升华】本题利用了:(1)折叠的性质:折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等;(2)平行线的性质.
【巩固练习】
一、选择题
1.下列命题中,真命题是( ).
A.任何数的绝对值都是正数 B.任何数的零次幂都等于1
C.互为倒数的两个数的和为零D.在数轴上表示的两个数,右边的数比左边的数大
2.一学员在广场上练习驾驶汽车,两次拐弯后行驶的方向与原来的方向相同,这两次拐弯的角度可能是( ) .
A.第一次向左拐30°,第二次向右拐30°
B.第一次向右拐50°,第二次向左拐130°
C.第一次向左拐50°,第二次向左拐130°
D.第一次向左拐50°,第二次向右拐130°
3.(2018春?通川区期末)如图,如果∠1=∠2,DE∥BC,则下列结论正确的个数为( )
(1)FG∥DC;(2)∠AED=∠ACB;(3)CD平分∠ACB;(4)∠1+∠B=90°;
(5)∠BFG=∠BDC.
A.1个 B.2个 C.3个 D.4个
4.两条平行直线被第三条直线所截时,产生的八个角中,角平分线互相平行的两个角是( ). A.同位角 B.同旁内角 C.内错角 D. 同位角或内错角
5.(2019?南湖区一模)如图,将△ABC沿DE,EF翻折,顶点A,B均落在点O处,且EA与EB重合于线段EO,若∠CDO+∠CFO=98°,则∠C的度数为( )
A.40° B.41° C.42° D.43°
6. 如图,已知∠A=∠C,如果要判断AB∥CD,则需要补充的条件是( ).
A.∠ABD=∠CEF B.∠CED=∠ADB
C.∠CDB=∠CEF D.∠ABD+∠CED=180°
7.如图,,则AEB=( ).
A. B. C. D.
8. 把一张对面互相平行的纸条折成如图所示,EF是折痕,若∠EFB=32°,则下列结论不正确的有( ).
A. B. ∠AEC=148° C. ∠BGE=64° D. ∠BFD=116°
二、填空题
9.(荆州二模)如图所示,AB∥CD,点E在CB的延长线上.若∠ECD=110°,则∠ABE的度数为________.
10.如图,l∥m,∠1=115°,∠2=95°,则∠3= .
11.如图所示,AB∥CD,MN交AB、CD于E、F,EG和FG分别是∠BEN和∠MFD的平分线,那么EG与FG的位置关系是 .
12.(2019春?南陵县期中)如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠1=30°,∠2=20°,则∠B= .
13.(2018春?苏州)如图所示,∠A=10°,∠ABC=90°,∠ACB=∠DCE,∠ADE=∠EDF,∠CED=∠FEG.则∠F= .
14. 我们已经证明了“三角形的内角等于180°”,易证“四边形的内角和等于360°=2×180°,五边形的内角和等于540°=3×180°,……”试猜想十边形的内角和等于
度.
15. 五角形的五个内角的和是________.
16. 如图,下面四个条件:(1),(2),(3),(4),
请你以其中两个论断为条件,一个论断为结论,组成一个真命题:如果 ,那么 .(只填序号即可)
三、解答题
17.如图所示,在平行四边形ABCD中,AQ,BN,CN,DQ分别是∠DAB,∠ABC,∠BCD,
∠CDA的平分线,AQ与BN交于P,CN与DQ交于M,在不添加其他条件的情况下,试写出一个由上述条件推出的结论,并给出证明过程.(推理过程中用到“平行四边形”和“角平分线”这两个条件)
18. 如图所示,已知∠1=50°,∠2=130°,∠4=50°,∠6=130°,试说明a∥b,b∥c,d∥e,a∥c.
19. 如图所示,已知AB∥CD,∠1=110°,∠2=125°,求∠x的大小.
20. (2018春?沛县期末)已知在四边形ABCD中,∠A=∠C=90°.
(1)∠ABC+∠ADC= ;
(2)如图1,若DE平分∠ABC的外角,BF平分∠ABC的外角,请写出DE与BF的位置关系,并证明.
(3)如图2,若BE、DE分别四等分∠ABC、∠ADC的外角(即∠CDE=∠CDN,∠CBE=∠CBM),试求∠E的度数.
【答案与解析】
一、选择题
1. 【答案】D;
2. 【答案】A;
【解析】首先根据题意对各选项画出示意图,观察图形,根据同位角相等,两直线平行,即可得出答案.
3. 【答案】C;
【解析】解:∵DE∥BC,∴∠DCB=∠1,∠AED=∠ACB,(2)正确;
∵∠1=∠2,∴∠2=∠DCB, ∴FG∥DC,(1)正确;∴∠BFG=∠BDC,(5)正确;
正确的个数有3个,故选:C.
4. 【答案】D;
【解析】三线八角中,角平分线互相平行的两角是同位角或内错角,互相垂直的两角是同旁内角.
5. 【答案】B;
【解析】解:如图,连接AO、BO.
由题意EA=EB=EO,
∴∠AOB=90°,∠OAB+∠OBA=90°,
∵DO=DA,FO=FB,
∴∠DAO=∠DOA,∠FOB=∠FBO,
∴∠CDO=2∠DAO,∠CFO=2∠FBO,
∵∠CDO+∠CFO=98°,
∴2∠DAO+2∠FBO=98°,
∴∠DAO+∠FBO=49°,
∴∠CAB+∠CBA=∠DAO+∠OAB+∠OBA+∠FBO=139°,
∴∠C=180°﹣(∠CAB+∠CBA)=180°﹣139°=41°,故选B.
6. 【答案】B;
7. 【答案】B;
【解析】∠EAB=75°-25°=50°.
8.【答案】B;
【解析】选项B中,∠AEC=180°-32°×2=116°,所以选项B错误.
二、填空题
9. 【答案】70°;
【解析】因AB∥CD,所以∠ABC=∠ECD=110°,所以∠ABE=180°-110°=70°.
10.【答案】150°;
【解析】∠1+∠2+∠3=360°,所以∠3=360°-(115°+95°)=150°.
11.【答案】垂直;
【解析】
解:EG⊥FG,理由如下:
∵ AB∥CD,∴ ∠BEN+∠MFD=180°.
∵ EG和FG分别是∠BEN和∠MFD的平分线,
∴ ∠GEN+∠GFM=(∠BEN+∠MFD)=×180°=90°.
∴ ∠EGF=180°-∠GEN-∠GFM=90°.
∴ EG⊥FG.
12.【答案】50°;
【解析】∵AE平分∠BAC,∴∠1=∠EAD+∠2,∴∠EAD=∠1﹣∠2=30°﹣20°=10°,
Rt△ABD中,∠B=90°﹣∠BAD=90°﹣30°﹣10°=50°.
13.【答案】70°;
14.【答案】1440°;
【解析】十边形的内角和:(10-2)×180°=1440°,
由此得n边形的内角和:(n-2)×180°.
15.【答案】180°;
【解析】如下图,∠A+∠C=∠2,∠B+∠D=∠1,而∠1+∠2+∠E=180°,从而得答案.
16.【答案】(2)(4),(1);(答案不唯一,只要答案合理即可)
【解析】通过证明全等可得答案.
三、解答题
17.【解析】
解:四边形PQMN为长方形. 在平行四边形ABCD中,∠ABC+∠BCD=180°, 又BN、CN分别平分∠ABC和∠BCD, ∴∠N=90°, 同理∠CMD=∠Q=∠APB=90°, 又∵∠CMD=∠NMQ,∠APB=∠NPQ, ∴四边形PQMN为长方形.
18.【解析】
解:因为∠1=50°,∠2=130°(已知),
所以∠1+∠2=180°.
所以a∥b(同旁内角互补,两直线平行).
所以∠3=∠1=50°(两直线平行,同位角相等).
又因为∠4=50°(已知),
所以∠3=∠4(等量代换).
所以d∥e(同位角相等,两直线平行).
因为∠5+∠6=180°(平角定义),∠6=130°(已知),
所以∠5=50°(等式的性质).
所以∠4=∠5(等量代换).
所以b∥c(内错角相等,两直线平行).
因为a∥b,b∥c(已知),
所以a∥c(平行于同一直线的两直线平行).
19.【解析】
解:过E点作EF∥AB,则∠3=180°-∠1=70°.
因为EF∥AB,AB∥CD,
所以EF∥CD.
所以∠4=180°-∠2=55°.
所以∠x=180°-∠3-∠4=55°.
20.【解析】
(1)解:∵∠A=∠C=90°,
∴∠ABC+∠ADC=360°﹣90°×2=180°;
故答案为:180°;
(2)解:延长DE交BF于G,
∵DE平分∠ADC,BF平分∠CBM,
∴∠CDE=∠ADC,∠CBF=∠CBM,
又∵∠CBM=180°﹣∠ABC=180°﹣(180°﹣∠ADC)=∠ADC,
∴∠CDE=∠CBF,
又∵∠BED=∠CDE+∠C=∠CBF+∠BGE,
∴∠BGE=∠C=90°,
∴DG⊥BF,
即DE⊥BF;
(3)解:由(1)得:∠CDN+∠CBM=180°,
∵BE、DE分别四等分∠ABC、∠ADC的外角,
∴∠CDE+∠CBE=×180°45°,
延长DC交BE于H,
由三角形的外角性质得,∠BHD=∠CDE+∠E,∠BCD=∠BHD+∠CBE,
∴∠BCD=∠CBE+∠CDE+∠E,
∴∠E=90°﹣45°=45°.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
