北师大版初中数学八年级上册知识讲解,巩固练习(教学资料,补习资料):第1讲 勾股定理(提高)含解析
文档属性
| 名称 | 北师大版初中数学八年级上册知识讲解,巩固练习(教学资料,补习资料):第1讲 勾股定理(提高)含解析 |  | |
| 格式 | zip | ||
| 文件大小 | 234.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-20 16:55:45 | ||
图片预览


文档简介
勾股定理(提高)
【学习目标】
1.掌握勾股定理的内容,了解勾股定理的多种证明方法,体验数形结合的思想;
2.能够运用勾股定理求解三角形中相关的边长(只限于常用的数);
3.通过对勾股定理的探索解决简单的实际问题,进一步运用方程思想解决问题.
【要点梳理】
要点一、勾股定理
直角三角形两条直角边的平方和等于斜边的平方.如果直角三角形的两直角边长分别为,斜边长为,那么.
要点诠释:(1)勾股定理揭示了一个直角三角形三边之间的数量关系.
(2)利用勾股定理,当设定一条直角边长为未知数后,根据题目已知的线段长可以建立方程求解,这样就将数与形有机地结合起来,达到了解决问题的目的.
(3)理解勾股定理的一些变式:
,, .
要点二、勾股定理的证明
方法一:将四个全等的直角三角形拼成如图(1)所示的正方形.
图(1)中,所以.
方法二:将四个全等的直角三角形拼成如图(2)所示的正方形.
图(2)中,所以.
方法三:如图(3)所示,将两个直角三角形拼成直角梯形.
,所以.
要点三、勾股定理的作用
已知直角三角形的任意两条边长,求第三边;
用于解决带有平方关系的证明问题;
3. 与勾股定理有关的面积计算;
4.勾股定理在实际生活中的应用.
【典型例题】
类型一、与勾股定理有关的证明
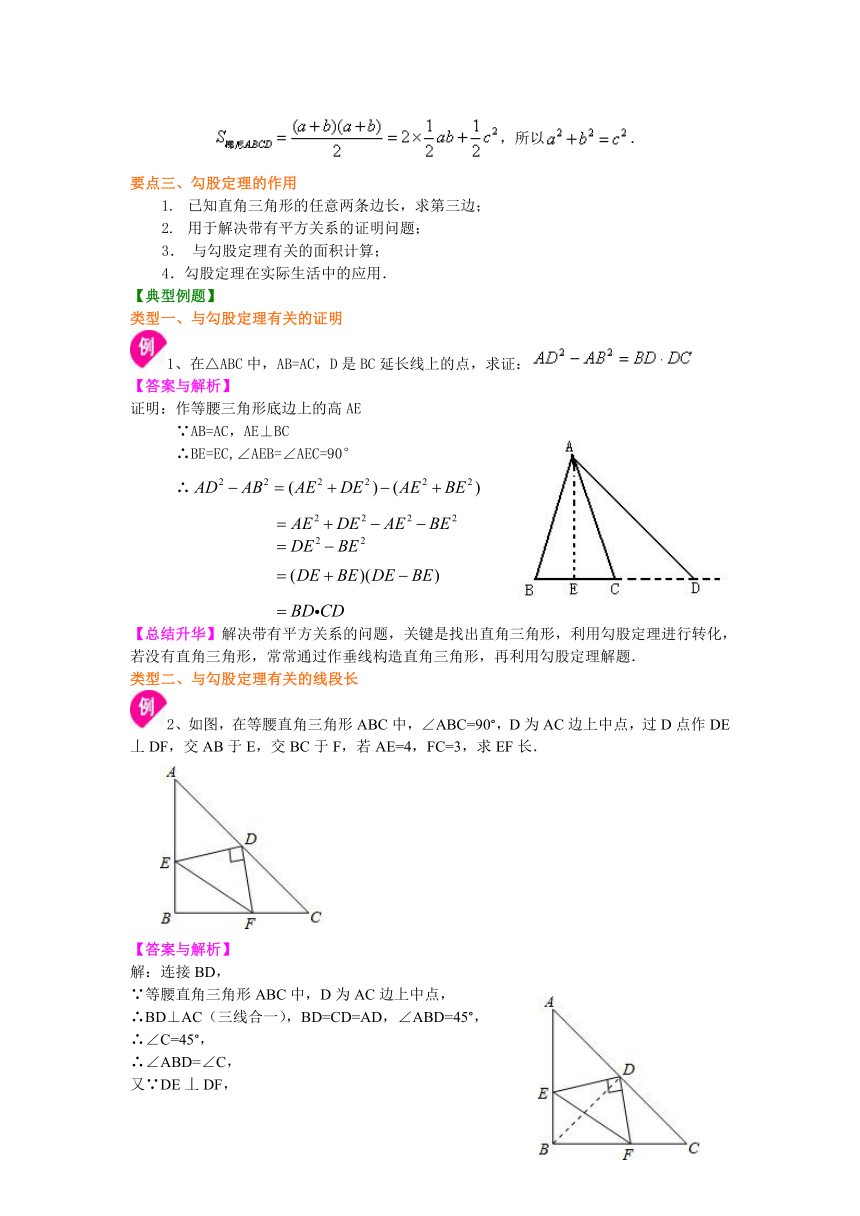
1、在△ABC中,AB=AC,D是BC延长线上的点,求证: 【答案与解析】
证明:作等腰三角形底边上的高AE ∵AB=AC,AE⊥BC
∴BE=EC,∠AEB=∠AEC=90°
∴
【总结升华】解决带有平方关系的问题,关键是找出直角三角形,利用勾股定理进行转化,若没有直角三角形,常常通过作垂线构造直角三角形,再利用勾股定理解题.
类型二、与勾股定理有关的线段长
2、如图,在等腰直角三角形ABC中,∠ABC=90°,D为AC边上中点,过D点作DE丄DF,交AB于E,交BC于F,若AE=4,FC=3,求EF长.
【答案与解析】
解:连接BD,
∵等腰直角三角形ABC中,D为AC边上中点,
∴BD⊥AC(三线合一),BD=CD=AD,∠ABD=45°,
∴∠C=45°,
∴∠ABD=∠C,
又∵DE丄DF,
∴∠FDC+∠BDF=∠EDB+∠BDF,
∴∠FDC=∠EDB,
在△EDB与△FDC中,
∵,
∴△EDB≌△FDC(ASA),
∴BE=FC=3,
∴AB=7,则BC=7,
∴BF=4,
在Rt△EBF中,
EF2=BE2+BF2=32+42,
∴EF=5.
【总结升华】此题考查的知识点是勾股定理及全等三角形的判定,关键是由已知先证三角形全等,求得BE和BF,再由勾股定理求出EF的长.
举一反三:
【变式】(2018春?天津校级期中)如图,∠C=30°,PA⊥OA于A,PB⊥OB于B,PA=2,PB=11,求OP的长.
【答案】
解:∵PA⊥OA,∠C=30°,
∴PC=2PA=4,
∴BC=BP+PC=11+4=15,
∵PB⊥OB,∠C=30°,
设OB=x,则OC=2x,
在Rt△BOC中,由勾股定理得:
x+15=(2x),
解得,x=5,
即OB=5,
∴OP===14.
类型三、与勾股定理有关的面积计算
3、(2018?丰台区二模)问题背景:
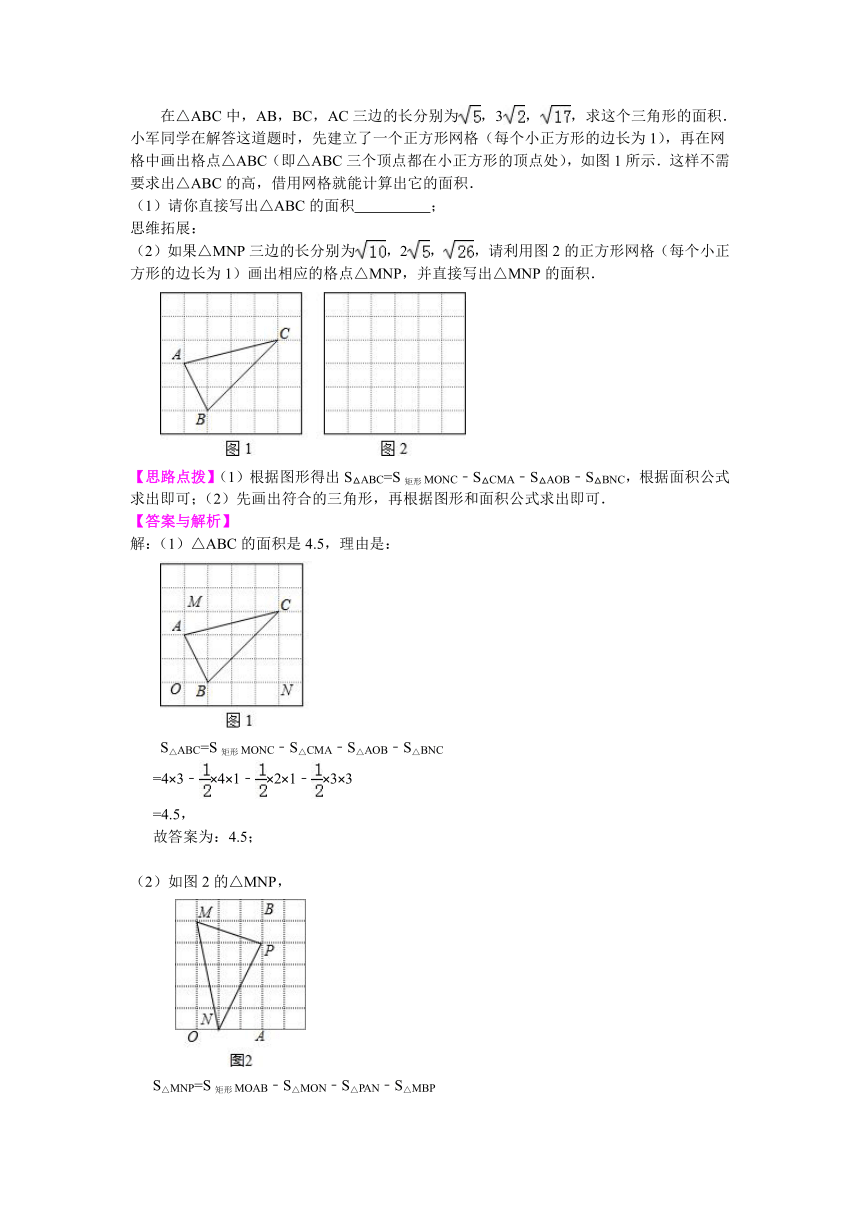
在△ABC中,AB,BC,AC三边的长分别为,3,,求这个三角形的面积.
小军同学在解答这道题时,先建立了一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需要求出△ABC的高,借用网格就能计算出它的面积.
(1)请你直接写出△ABC的面积 ;
思维拓展:
(2)如果△MNP三边的长分别为,2,,请利用图2的正方形网格(每个小正方形的边长为1)画出相应的格点△MNP,并直接写出△MNP的面积.
【思路点拨】(1)根据图形得出S△ABC=S矩形MONC﹣S△CMA﹣S△AOB﹣S△BNC,根据面积公式求出即可;(2)先画出符合的三角形,再根据图形和面积公式求出即可.
【答案与解析】
解:(1)△ABC的面积是4.5,理由是:
S△ABC=S矩形MONC﹣S△CMA﹣S△AOB﹣S△BNC
=4×3﹣×4×1﹣×2×1﹣×3×3
=4.5,
故答案为:4.5;
(2)如图2的△MNP,
S△MNP=S矩形MOAB﹣S△MON﹣S△PAN﹣S△MBP
=5×3﹣×5×1﹣×2×4﹣×3×1
=7,
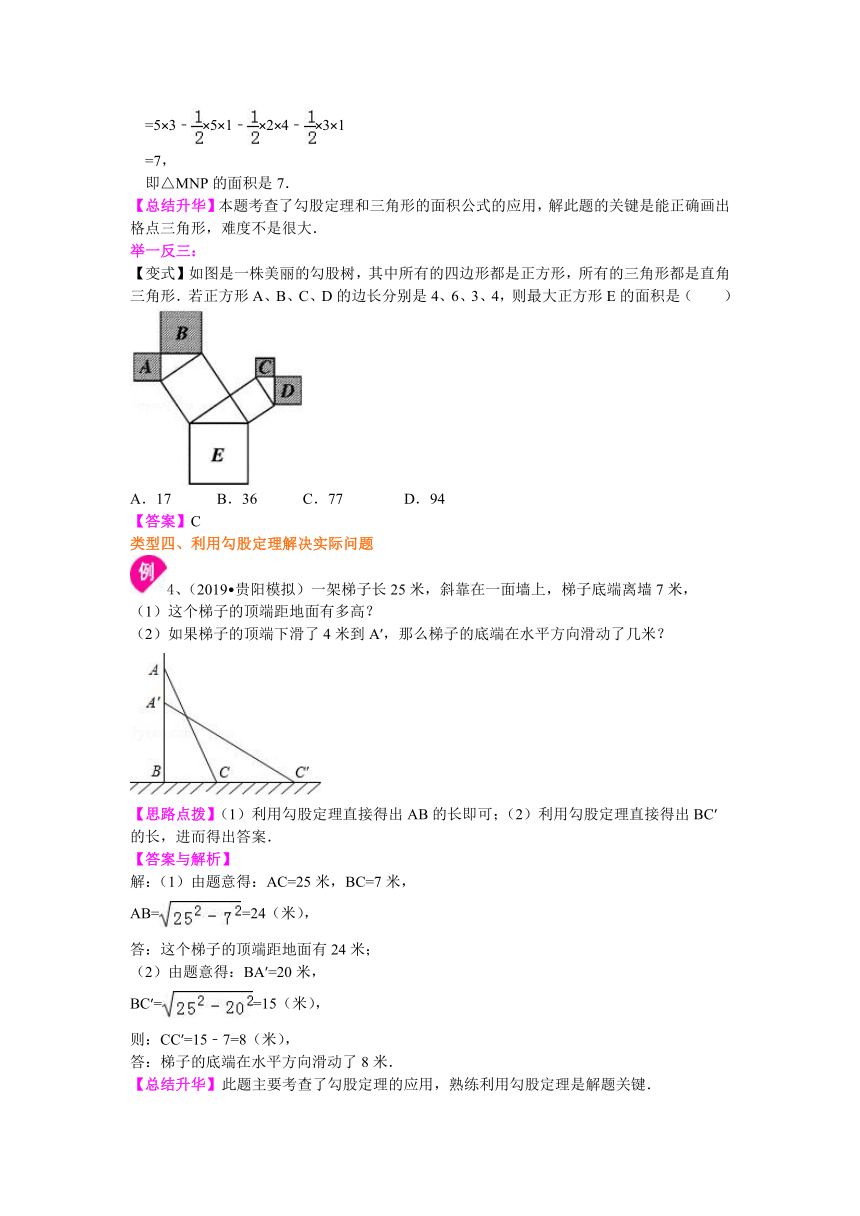
即△MNP的面积是7.
【总结升华】本题考查了勾股定理和三角形的面积公式的应用,解此题的关键是能正确画出格点三角形,难度不是很大.
举一反三:
【变式】如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是4、6、3、4,则最大正方形E的面积是( )
A.17 B.36 C.77 D.94
【答案】C
类型四、利用勾股定理解决实际问题
4、(2019?贵阳模拟)一架梯子长25米,斜靠在一面墙上,梯子底端离墙7米,
(1)这个梯子的顶端距地面有多高?
(2)如果梯子的顶端下滑了4米到A′,那么梯子的底端在水平方向滑动了几米?
【思路点拨】(1)利用勾股定理直接得出AB的长即可;(2)利用勾股定理直接得出BC′的长,进而得出答案.
【答案与解析】
解:(1)由题意得:AC=25米,BC=7米,
AB==24(米),
答:这个梯子的顶端距地面有24米;
(2)由题意得:BA′=20米,
BC′==15(米),
则:CC′=15﹣7=8(米),
答:梯子的底端在水平方向滑动了8米.
【总结升华】此题主要考查了勾股定理的应用,熟练利用勾股定理是解题关键.
举一反三:
【变式】如图①,有一个圆柱,它的高等于12,底面半径等于3,在圆柱的底面A点有一只蚂蚁,它想吃到上底面上与A点相对的B点的食物,需要爬行的最短路程是多少?(π取3)
【答案】
解:如图②所示,由题意可得:
,
在Rt△AA′B中,根据勾股定理得:
则AB=15.
所以需要爬行的最短路程是15.
勾股定理(提高)
【巩固练习】
一.选择题
1.如图,△ABC中,D为AB中点,E在AC上,且BE⊥AC.若DE=10,AE=16,则BE的长度为( )
A.10 B.11 C.12 D.13
2. (2019?漳州)如图,△ABC中,AB=AC=5,BC=8,D是线段BC上的动点(不含端点B、C).若线段AD长为正整数,则点D的个数共有( )
A.5个 B.4个 C.3个 D.2个
3.如图,长方形AOBC中,AO=8,BD=3,若将矩形沿直线AD折叠,则顶点C恰好落在边OB上E处,那么图中阴影部分的面积为( )
A.30 B.32 C.34 D.16
4.如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线,,上,且,之间的距离为2 , ,之间的距离为3 ,则的值是( )
A.68 B.20 C.32 D.47
5.在△ABC中,AB=15,AC=13,高AD=12,则△ABC的周长为( )
A.42 B.32 C.42或32 D.37或33
6.(2018?烟台)如图,正方形ABCD的边长为2,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…按照此规律继续下去,则S2018的值为( )
A. B. C. D.
二.填空题
7.若一个直角三角形的两边长分别为12和5,则此三角形的第三边的平方为______.
8. 将一根长为15cm的很细的木棒置于底面直径为5cm,高为12cm的圆柱形杯中,木棒露在杯子外面的部分长度x的范围是 .
9.如图,在的正方形网格中,以AB为边画直角△ABC,使点C在格点上,这样的点C共 个.
10.(2019?黄冈校级自助招生)如图,它是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形.如果大正方形的面积是13,小正方形的面积是1,直角三角形较短的直角边长为a,较长的直角边长为b,那么(a+b)2的值是 _________ .
11.已知长方形ABCD,AB=3,AD=4,过对角线BD的中点O做BD的垂直平分线EF,分别交AD、BC于点E、F,则AE的长为_______________.
12.(2018春?召陵区期中)如图,在四边形ABCD中,AB=3,BC=4,CD=12,AD=13,∠B=90°,那么四边形ABCD的面积是 .
三.解答题
13.(2018?青岛模拟)如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,求运动过程中,点D到点O的最大距离.
14.现有10个边长为1的正方形,排列形式如左下图, 请把它们分割后拼接成一个新的正方形.要求: 在左下图中用实线画出分割线, 并在右下图的正方形网格图(图中每个小正方形的边长均为1)中用实线画出拼接成的新正方形.
15.由于过度采伐森林和破坏植被,我国部分地区频频遭受沙尘暴的侵袭.近日,A城气象局测得沙尘暴中心在A城的正西方向240km的B处,以每时12km的速度向北偏东60°方向移动,距沙尘暴中心150km的范围为受影响区域. (1)A城是否受到这次沙尘暴的影响?为什么? (2)若A城受这次沙尘暴影响,那么遭受影响的时间有多长?
【答案与解析】
一.选择题
1. 【答案】C
【解析】∵BE⊥AC,∴△AEB是直角三角形,∵D为AB中点,DE=10,∴AB=20,∵AE=16,,所以BE=12.
2. 【答案】C
【解析】过点A作AE⊥BC,则由勾股定理得AE=3,点D是线段BC上的动点(不含端点B、C).所以3≤AD<5,AD=3或4,共有3个符合条件的点.
3.【答案】A
【解析】由题意CD=DE=5,BE=4,设OE=,AE=AC=,所以,,阴影部分面积为.
4.【答案】A
【解析】如图,分别作CD⊥交于点E,作AF⊥,则可证△AFB≌△BDC,则AF=3=BD, BF=CD=2+3=5,∴DF=5+3=8=AE,在直角△AEC中,勾股定理得.
5.【答案】C
【解析】高在△ABC内部,第三边长为14;高在△ABC外部,第三边长为4,故选C.
6.【答案】C
【解析】解:根据题意:第一个正方形的边长为2;
第二个正方形的边长为:;
第三个正方形的边长为:,
…
第n个正方形的边长是,
所以S2018的值是()2012,
故选C.
二.填空题
7.【答案】169或119;
【解析】没有指明这两边为直角边,所以要分类讨论,12也可能是斜边.
8.【答案】2cm≤x≤3cm;
【解析】由题意可知BC=5cm,AC=12cm,AB=13cm.当木棒垂直于底面时露在杯子外面的部分长度最长为,15-AC=15-12=3cm,当木棒与AB重合时露在杯子外面的部分长度最短为15-AB=15-13=2cm.
9.【答案】8;
【解析】如图所示:有8个点满足要求.
10.【答案】25;
【解析】根据题意,结合勾股定理a2+b2=13,四个三角形的面积=4×ab=13﹣1,∴2ab=12,联立解得:(a+b)2=13+12=25.
11.【答案】;
【解析】连接BE,设AE=,BE=DE=,则,.
12.【答案】36.
【解析】解:∵∠ABC=90°,AB=3,BC=4,
∴AC===5,
在△ACD中,AC2+CD2=25+144=169=AD2,
∴△ACD是直角三角形,
∴S四边形ABCD=AB?BC+AC?CD
=×3×4+×5×12
=36.
故答案是:36.
三.解答题
13.【解析】解:如图,取AB的中点E,连接OE、DE、OD,
∵OD≤OE+DE,
∴当O、D、E三点共线时,点D到点O的距离最大,
此时,∵AB=2,BC=1,
∴OE=AE=AB=1,
DE===,
∴OD的最大值为:+1.
14.【解析】
解:如图所示:
15.【解析】
解:(1)过点A作AC⊥BM,垂足为C, 在Rt△ABC中,由题意可知∠CBA=30°, ∴AC=AB=×240=120, ∵AC=120<150, ∴A城将受这次沙尘暴的影响. (2)设点E,F是以A为圆心,150km为半径的圆与MB的交点,连接AE,AF, 由题意得,,CE=90 ∴EF=2CE=2×90=180
180÷12=15(小时) ∴A城受沙尘暴影响的时间为15小时.
【学习目标】
1.掌握勾股定理的内容,了解勾股定理的多种证明方法,体验数形结合的思想;
2.能够运用勾股定理求解三角形中相关的边长(只限于常用的数);
3.通过对勾股定理的探索解决简单的实际问题,进一步运用方程思想解决问题.
【要点梳理】
要点一、勾股定理
直角三角形两条直角边的平方和等于斜边的平方.如果直角三角形的两直角边长分别为,斜边长为,那么.
要点诠释:(1)勾股定理揭示了一个直角三角形三边之间的数量关系.
(2)利用勾股定理,当设定一条直角边长为未知数后,根据题目已知的线段长可以建立方程求解,这样就将数与形有机地结合起来,达到了解决问题的目的.
(3)理解勾股定理的一些变式:
,, .
要点二、勾股定理的证明
方法一:将四个全等的直角三角形拼成如图(1)所示的正方形.
图(1)中,所以.
方法二:将四个全等的直角三角形拼成如图(2)所示的正方形.
图(2)中,所以.
方法三:如图(3)所示,将两个直角三角形拼成直角梯形.
,所以.
要点三、勾股定理的作用
已知直角三角形的任意两条边长,求第三边;
用于解决带有平方关系的证明问题;
3. 与勾股定理有关的面积计算;
4.勾股定理在实际生活中的应用.
【典型例题】
类型一、与勾股定理有关的证明
1、在△ABC中,AB=AC,D是BC延长线上的点,求证: 【答案与解析】
证明:作等腰三角形底边上的高AE ∵AB=AC,AE⊥BC
∴BE=EC,∠AEB=∠AEC=90°
∴
【总结升华】解决带有平方关系的问题,关键是找出直角三角形,利用勾股定理进行转化,若没有直角三角形,常常通过作垂线构造直角三角形,再利用勾股定理解题.
类型二、与勾股定理有关的线段长
2、如图,在等腰直角三角形ABC中,∠ABC=90°,D为AC边上中点,过D点作DE丄DF,交AB于E,交BC于F,若AE=4,FC=3,求EF长.
【答案与解析】
解:连接BD,
∵等腰直角三角形ABC中,D为AC边上中点,
∴BD⊥AC(三线合一),BD=CD=AD,∠ABD=45°,
∴∠C=45°,
∴∠ABD=∠C,
又∵DE丄DF,
∴∠FDC+∠BDF=∠EDB+∠BDF,
∴∠FDC=∠EDB,
在△EDB与△FDC中,
∵,
∴△EDB≌△FDC(ASA),
∴BE=FC=3,
∴AB=7,则BC=7,
∴BF=4,
在Rt△EBF中,
EF2=BE2+BF2=32+42,
∴EF=5.
【总结升华】此题考查的知识点是勾股定理及全等三角形的判定,关键是由已知先证三角形全等,求得BE和BF,再由勾股定理求出EF的长.
举一反三:
【变式】(2018春?天津校级期中)如图,∠C=30°,PA⊥OA于A,PB⊥OB于B,PA=2,PB=11,求OP的长.
【答案】
解:∵PA⊥OA,∠C=30°,
∴PC=2PA=4,
∴BC=BP+PC=11+4=15,
∵PB⊥OB,∠C=30°,
设OB=x,则OC=2x,
在Rt△BOC中,由勾股定理得:
x+15=(2x),
解得,x=5,
即OB=5,
∴OP===14.
类型三、与勾股定理有关的面积计算
3、(2018?丰台区二模)问题背景:
在△ABC中,AB,BC,AC三边的长分别为,3,,求这个三角形的面积.
小军同学在解答这道题时,先建立了一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需要求出△ABC的高,借用网格就能计算出它的面积.
(1)请你直接写出△ABC的面积 ;
思维拓展:
(2)如果△MNP三边的长分别为,2,,请利用图2的正方形网格(每个小正方形的边长为1)画出相应的格点△MNP,并直接写出△MNP的面积.
【思路点拨】(1)根据图形得出S△ABC=S矩形MONC﹣S△CMA﹣S△AOB﹣S△BNC,根据面积公式求出即可;(2)先画出符合的三角形,再根据图形和面积公式求出即可.
【答案与解析】
解:(1)△ABC的面积是4.5,理由是:
S△ABC=S矩形MONC﹣S△CMA﹣S△AOB﹣S△BNC
=4×3﹣×4×1﹣×2×1﹣×3×3
=4.5,
故答案为:4.5;
(2)如图2的△MNP,
S△MNP=S矩形MOAB﹣S△MON﹣S△PAN﹣S△MBP
=5×3﹣×5×1﹣×2×4﹣×3×1
=7,
即△MNP的面积是7.
【总结升华】本题考查了勾股定理和三角形的面积公式的应用,解此题的关键是能正确画出格点三角形,难度不是很大.
举一反三:
【变式】如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是4、6、3、4,则最大正方形E的面积是( )
A.17 B.36 C.77 D.94
【答案】C
类型四、利用勾股定理解决实际问题
4、(2019?贵阳模拟)一架梯子长25米,斜靠在一面墙上,梯子底端离墙7米,
(1)这个梯子的顶端距地面有多高?
(2)如果梯子的顶端下滑了4米到A′,那么梯子的底端在水平方向滑动了几米?
【思路点拨】(1)利用勾股定理直接得出AB的长即可;(2)利用勾股定理直接得出BC′的长,进而得出答案.
【答案与解析】
解:(1)由题意得:AC=25米,BC=7米,
AB==24(米),
答:这个梯子的顶端距地面有24米;
(2)由题意得:BA′=20米,
BC′==15(米),
则:CC′=15﹣7=8(米),
答:梯子的底端在水平方向滑动了8米.
【总结升华】此题主要考查了勾股定理的应用,熟练利用勾股定理是解题关键.
举一反三:
【变式】如图①,有一个圆柱,它的高等于12,底面半径等于3,在圆柱的底面A点有一只蚂蚁,它想吃到上底面上与A点相对的B点的食物,需要爬行的最短路程是多少?(π取3)
【答案】
解:如图②所示,由题意可得:
,
在Rt△AA′B中,根据勾股定理得:
则AB=15.
所以需要爬行的最短路程是15.
勾股定理(提高)
【巩固练习】
一.选择题
1.如图,△ABC中,D为AB中点,E在AC上,且BE⊥AC.若DE=10,AE=16,则BE的长度为( )
A.10 B.11 C.12 D.13
2. (2019?漳州)如图,△ABC中,AB=AC=5,BC=8,D是线段BC上的动点(不含端点B、C).若线段AD长为正整数,则点D的个数共有( )
A.5个 B.4个 C.3个 D.2个
3.如图,长方形AOBC中,AO=8,BD=3,若将矩形沿直线AD折叠,则顶点C恰好落在边OB上E处,那么图中阴影部分的面积为( )
A.30 B.32 C.34 D.16
4.如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线,,上,且,之间的距离为2 , ,之间的距离为3 ,则的值是( )
A.68 B.20 C.32 D.47
5.在△ABC中,AB=15,AC=13,高AD=12,则△ABC的周长为( )
A.42 B.32 C.42或32 D.37或33
6.(2018?烟台)如图,正方形ABCD的边长为2,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…按照此规律继续下去,则S2018的值为( )
A. B. C. D.
二.填空题
7.若一个直角三角形的两边长分别为12和5,则此三角形的第三边的平方为______.
8. 将一根长为15cm的很细的木棒置于底面直径为5cm,高为12cm的圆柱形杯中,木棒露在杯子外面的部分长度x的范围是 .
9.如图,在的正方形网格中,以AB为边画直角△ABC,使点C在格点上,这样的点C共 个.
10.(2019?黄冈校级自助招生)如图,它是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形.如果大正方形的面积是13,小正方形的面积是1,直角三角形较短的直角边长为a,较长的直角边长为b,那么(a+b)2的值是 _________ .
11.已知长方形ABCD,AB=3,AD=4,过对角线BD的中点O做BD的垂直平分线EF,分别交AD、BC于点E、F,则AE的长为_______________.
12.(2018春?召陵区期中)如图,在四边形ABCD中,AB=3,BC=4,CD=12,AD=13,∠B=90°,那么四边形ABCD的面积是 .
三.解答题
13.(2018?青岛模拟)如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,求运动过程中,点D到点O的最大距离.
14.现有10个边长为1的正方形,排列形式如左下图, 请把它们分割后拼接成一个新的正方形.要求: 在左下图中用实线画出分割线, 并在右下图的正方形网格图(图中每个小正方形的边长均为1)中用实线画出拼接成的新正方形.
15.由于过度采伐森林和破坏植被,我国部分地区频频遭受沙尘暴的侵袭.近日,A城气象局测得沙尘暴中心在A城的正西方向240km的B处,以每时12km的速度向北偏东60°方向移动,距沙尘暴中心150km的范围为受影响区域. (1)A城是否受到这次沙尘暴的影响?为什么? (2)若A城受这次沙尘暴影响,那么遭受影响的时间有多长?
【答案与解析】
一.选择题
1. 【答案】C
【解析】∵BE⊥AC,∴△AEB是直角三角形,∵D为AB中点,DE=10,∴AB=20,∵AE=16,,所以BE=12.
2. 【答案】C
【解析】过点A作AE⊥BC,则由勾股定理得AE=3,点D是线段BC上的动点(不含端点B、C).所以3≤AD<5,AD=3或4,共有3个符合条件的点.
3.【答案】A
【解析】由题意CD=DE=5,BE=4,设OE=,AE=AC=,所以,,阴影部分面积为.
4.【答案】A
【解析】如图,分别作CD⊥交于点E,作AF⊥,则可证△AFB≌△BDC,则AF=3=BD, BF=CD=2+3=5,∴DF=5+3=8=AE,在直角△AEC中,勾股定理得.
5.【答案】C
【解析】高在△ABC内部,第三边长为14;高在△ABC外部,第三边长为4,故选C.
6.【答案】C
【解析】解:根据题意:第一个正方形的边长为2;
第二个正方形的边长为:;
第三个正方形的边长为:,
…
第n个正方形的边长是,
所以S2018的值是()2012,
故选C.
二.填空题
7.【答案】169或119;
【解析】没有指明这两边为直角边,所以要分类讨论,12也可能是斜边.
8.【答案】2cm≤x≤3cm;
【解析】由题意可知BC=5cm,AC=12cm,AB=13cm.当木棒垂直于底面时露在杯子外面的部分长度最长为,15-AC=15-12=3cm,当木棒与AB重合时露在杯子外面的部分长度最短为15-AB=15-13=2cm.
9.【答案】8;
【解析】如图所示:有8个点满足要求.
10.【答案】25;
【解析】根据题意,结合勾股定理a2+b2=13,四个三角形的面积=4×ab=13﹣1,∴2ab=12,联立解得:(a+b)2=13+12=25.
11.【答案】;
【解析】连接BE,设AE=,BE=DE=,则,.
12.【答案】36.
【解析】解:∵∠ABC=90°,AB=3,BC=4,
∴AC===5,
在△ACD中,AC2+CD2=25+144=169=AD2,
∴△ACD是直角三角形,
∴S四边形ABCD=AB?BC+AC?CD
=×3×4+×5×12
=36.
故答案是:36.
三.解答题
13.【解析】解:如图,取AB的中点E,连接OE、DE、OD,
∵OD≤OE+DE,
∴当O、D、E三点共线时,点D到点O的距离最大,
此时,∵AB=2,BC=1,
∴OE=AE=AB=1,
DE===,
∴OD的最大值为:+1.
14.【解析】
解:如图所示:
15.【解析】
解:(1)过点A作AC⊥BM,垂足为C, 在Rt△ABC中,由题意可知∠CBA=30°, ∴AC=AB=×240=120, ∵AC=120<150, ∴A城将受这次沙尘暴的影响. (2)设点E,F是以A为圆心,150km为半径的圆与MB的交点,连接AE,AF, 由题意得,,CE=90 ∴EF=2CE=2×90=180
180÷12=15(小时) ∴A城受沙尘暴影响的时间为15小时.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
