北师大版初中数学八年级上册知识讲解,巩固练习(教学资料,补习资料):第2讲 勾股定理逆定理(提高)(含答案)
文档属性
| 名称 | 北师大版初中数学八年级上册知识讲解,巩固练习(教学资料,补习资料):第2讲 勾股定理逆定理(提高)(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 204.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-20 17:15:37 | ||
图片预览




文档简介
勾股定理的逆定理(提高)
【学习目标】
1. 理解勾股定理的逆定理,并能与勾股定理相区别;
2. 能运用勾股定理的逆定理判断一个三角形是否是直角三角形;
3. 理解勾股数的含义;
4. 通过探索直角三角形的判定条件的过程,培养动手操作能力和逻辑推理能力.
【要点梳理】
要点一、勾股定理的逆定理
如果三角形的三条边长,满足,那么这个三角形是直角三角形.
要点诠释:(1)勾股定理的逆定理的作用是判定某一个三角形是否是直角三角形.
(2)勾股定理的逆定理是把“数”转为“形”,是通过计算来判定一个三角形是否为直角三角形.
要点二、如何判定一个三角形是否是直角三角形
首先确定最大边(如).
验证与是否具有相等关系.若,则△ABC是∠C=90°的直角三角形;若,则△ABC不是直角三角形.
要点诠释:当时,此三角形为钝角三角形;当时,此三角形为锐角三角形,其中为三角形的最大边.
要点三、勾股数
满足不定方程的三个正整数,称为勾股数(又称为高数或毕达哥拉斯数),显然,以为三边长的三角形一定是直角三角形.
熟悉下列勾股数,对解题会很有帮助:
3、4、5; ②5、12、13;③8、15、17;④7、24、25;⑤9、40、41……
如果是勾股数,当为正整数时,以为三角形的三边长,此三角形必为直角三角形.
要点诠释:(1)(是自然数)是直角三角形的三条边长;
(2)(是自然数)是直角三角形的三条边长;
(3) (是自然数)是直角三角形的三条边长;
【典型例题】
类型一、勾股定理的逆定理
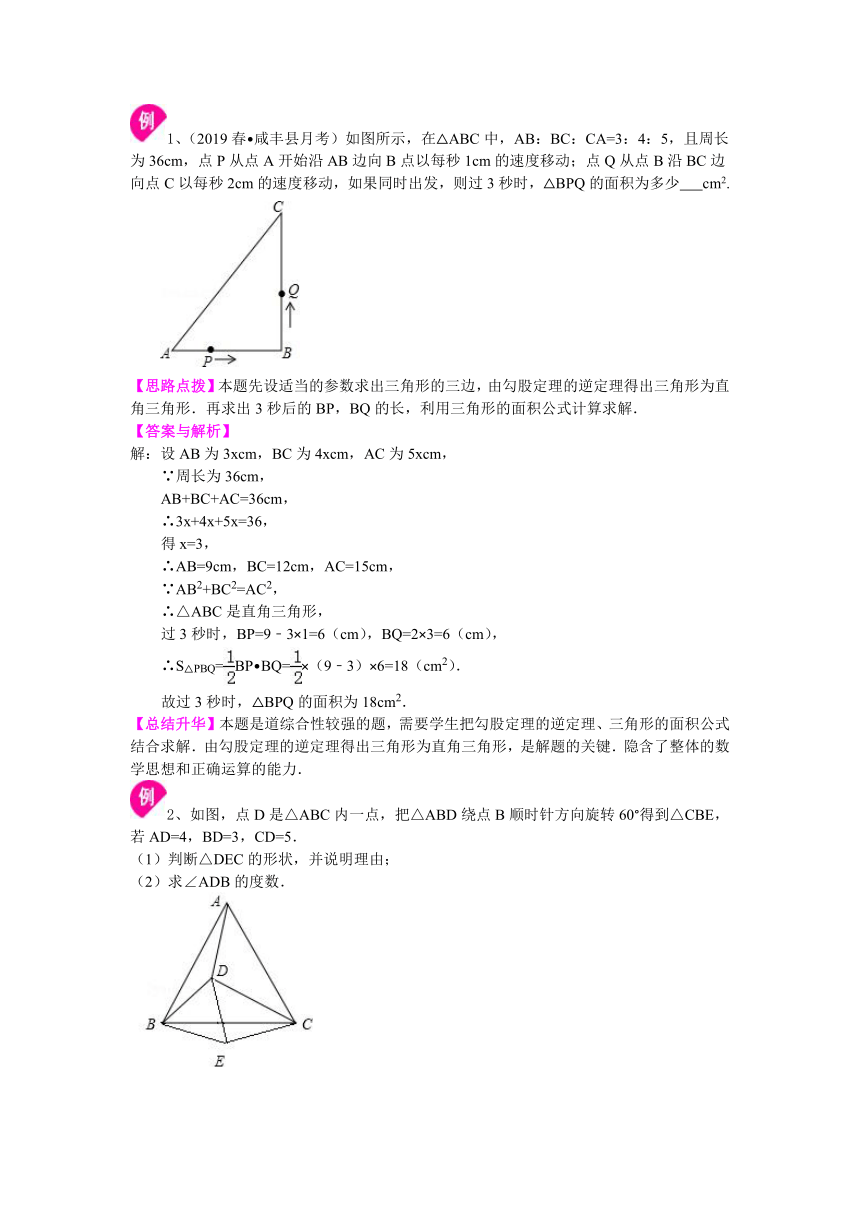
1、(2019春?咸丰县月考)如图所示,在△ABC中,AB:BC:CA=3:4:5,且周长为36cm,点P从点A开始沿AB边向B点以每秒1cm的速度移动;点Q从点B沿BC边向点C以每秒2cm的速度移动,如果同时出发,则过3秒时,△BPQ的面积为多少 cm2.
【思路点拨】本题先设适当的参数求出三角形的三边,由勾股定理的逆定理得出三角形为直角三角形.再求出3秒后的BP,BQ的长,利用三角形的面积公式计算求解.
【答案与解析】
解:设AB为3xcm,BC为4xcm,AC为5xcm,
∵周长为36cm,
AB+BC+AC=36cm,
∴3x+4x+5x=36,
得x=3,
∴AB=9cm,BC=12cm,AC=15cm,
∵AB2+BC2=AC2,
∴△ABC是直角三角形,
过3秒时,BP=9﹣3×1=6(cm),BQ=2×3=6(cm),
∴S△PBQ=BP?BQ=×(9﹣3)×6=18(cm2).
故过3秒时,△BPQ的面积为18cm2.
【总结升华】本题是道综合性较强的题,需要学生把勾股定理的逆定理、三角形的面积公式结合求解.由勾股定理的逆定理得出三角形为直角三角形,是解题的关键.隐含了整体的数学思想和正确运算的能力.
2、如图,点D是△ABC内一点,把△ABD绕点B顺时针方向旋转60°得到△CBE,若AD=4,BD=3,CD=5.
(1)判断△DEC的形状,并说明理由;
(2)求∠ADB的度数.
【思路点拨】把△ABD绕点B顺时针方向旋转60°,注意旋转只是三角形的位置变了,三角形的边长和角度并没有变,并且旋转的角度60°,因此出现等边△BDE,从而才能更有利的判断三角形的形状和求∠ADB的度数.
【答案与解析】
解:(1)根据图形的旋转不变性,
AD=EC,BD=BE,
又∵∠DBE=∠ABC=60°,
∴△ABC和△DBE均为等边三角形,
于是DE=BD=3,EC=AD=4,
又∵CD=5,
∴DE2+EC2=32+42=52=CD2;
故△DEC为直角三角形.
(2)∵△DEC为直角三角形,
∴∠DEC=90°,
又∵△BDE为等边三角形,
∴∠BED=60°,
∴∠BEC=90°+60°=150°,
即∠ADB=150°.
【总结升华】此题考查了旋转后图形的不变性、全等三角形的性质、等边三角形的性质、勾股定理的逆定理等知识,综合性较强,是一道好题.解答(2)时要注意运用(1)的结论.
举一反三:
【变式】如图所示,在△ABC中,已知∠ACB=90°,AC=BC,P是△ABC内一点,且PA=3,PB=1,PC=CD=2,CD⊥CP,求∠BPC的度数.
【答案】
解:连接BD.∵ CD⊥CP,且CD=CP=2,
∴ △CPD为等腰直角三角形,即∠CPD=45°.
∵ ∠ACP+∠BCP=∠BCP+∠BCD=90°,
∴ ∠ACP=∠BCD.
∵ CA=CB,
∴ △CAP≌△CBD(SAS),
∴ DB=PA=3.
在Rt△CPD中,.
又∵ PB=1,则.
∵ ,
∴ ,
∴ △DPB为直角三角形,且∠DPB=90°,
∴ ∠CPB=∠CPD+∠DPB=45°+90°=135°.
类型二、勾股定理逆定理的应用
3、已知a、b、c是△ABC的三边,且满足,且a+b+c=12,请你探索△ABC的形状.
【答案与解析】
解:令=k.
∴a+4=3k,b+3=2k,c+8=4k,
∴a=3k﹣4,b=2k﹣3,c=4k﹣8.
又∵a+b+c=12,
∴(3k﹣4)+(2k﹣3)+(4k﹣8)=12,
∴k=3.
∴a=5,b=3,c=4.
∴△ABC是直角三角形.
【总结升华】此题借用设比例系数k的方法,进一步求得三角形的三边长,根据勾股定理的逆定理判定三角形的形状.
举一反三:
【变式】(2018春?渝中区校级月考)△ABC的三边a、b、c满足|a+b﹣50|++(c﹣40)2=0.试判断△ABC的形状是 .
【答案】直角三角形.
解:∵|a+b﹣50|++(c﹣40)2=0,
∴,
解得,
∵92+402=412,
∴△ABC是直角三角形.
故答案为直角三角形.
4、如图所示,MN以左为我国领海,以右为公海,上午9时50分我国缉私艇A发现在其正东方向有一走私艇C并以每小时13海里的速度偷偷向我国领海开来,便立即通知距其5海里,并在MN线上巡逻的缉私艇B密切注意,并告知A和C两艇的距离是13海里,缉私艇B测得C与其距离为12海里,若走私艇C的速度不变,最早在什么时间进入我国海域?
【答案与解析】
解:∵ ,
∴ △ABC为直角三角形.∴ ∠ABC=90°.
又BD⊥AC,可设CD=,
∴
①-②得,
解得.∴ ≈0.85(h)=51(分).
所以走私艇最早在10时41分进入我国领海.
【总结升华】(1)本题用勾股定理作相等关系列方程解决问题,(2)用勾股定理的逆定理判定直角三角形,为勾股定理的运用提供了条件.
【巩固练习】
一.选择题
1.(2019春?平武县校级月考)下列各组数中,可以构成勾股数的是( )
A.13,16,19 B.,, C.18,24,36 D.12,35,37
2.(2018春?凉山州期末)△ABC中,∠A,∠B,∠C所对的边分别是a,b,c,满足下列条件的△ABC,不是直角三角形的是( )
A.a:b:c=1::1 B.∠A:∠B:∠C=3:4:5
C.(a+b)(a﹣b)=c D.∠A:∠B:∠C=1:2:3
3. 已知△ABC三边长分别为2n+1,2n2+2n,2n2+2n+1,(n为正整数),则△ABC为( )
A.
直角三角形
B.
等腰三角形
C.
锐角三角形
D.
钝角三角形
4. 有下面的判断:①△ABC中,a2+b2≠c2,则△ABC不是直角三角形.②△ABC是直角三角形,∠C=90°,则a2+b2=c2.③若△ABC中,a2﹣b2=c2,则△ABC是直角三角形.④若△ABC是直角三角形,则(a+b)(a﹣b)=c2.以上判断正确的有( )
A.
4个
B.
3个
C.
2个
D.
1个
5.五根小木棒,其长度分别为7,15,20,24,25,现将他们摆成两个直角三角形,其中正确的是( )
6. 为直角三角形的三边,且为斜边,为斜边上的高,下列说法:
①能组成一个三角形 ②能组成直角三角形
③能组成直角三角形 ④三个内角的度数之比为3:4:5能组成一个三角形
其中正确结论的个数是( )
A.1 B.2 C.3 D.4
二.填空题
7.若△ABC中,,则∠B=____________.
8.(2019春?罗定市期中)若△ABC的三边长分别为x+1,x+2,x+3,要使此三角形成为直角三角形,则x= .
9.若一个三角形的三边长分别为1、、8(其中为正整数),则以、、为边的三角形的面积为______.
10.△ABC的两边分别为5,12,另一边为奇数,且是3的倍数,则应为______,此三角形为______.
11.(2018春?寿县期中)在某港口有甲乙两艘渔船,若甲沿北偏东60°方向以每小时8海里的速度前进,同时,乙船沿南偏东角度以每小时15海里速度前进,2小时后,甲乙两船相距34海里,那么,乙船航行的方向是南偏东___________度.
12. 如果线段能组成一个直角三角形,那么________组成直角三角形.(填“能”或“不能”).
三.解答题
13.(2018秋?广州校级期末)如图,已知某经济开发区有一块四边形空地ABCD,现计划在该空地上种植草皮,经测量∠A=90°,AB=300m,AD=400m,CD=1300m,BC=1200m.请计算种植草皮的面积.
14.在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别是a、b、c.
(1)填表:
边a、b、c
三角形的面积与周长的比值
3 4 5
5 12 13
8 15 17
(2)若a+b﹣c=m,则猜想= (并证明此结论).
15. 我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.
(1)写出你所学过的特殊四边形中是勾股四边形的两种图形的名称正方形、长方形、直角梯形(任选两个均可);
(2)如图1,已知格点(小正方形的顶点)O(0,0),A(3,0),B(0,4),请你画出以格点为顶点,OA,OB为勾股边且对角线相等的勾股四边形OAMB;
(3)如图2,将△ABC绕顶点B按顺时针方向旋转60°,得到△DBE,连接AD,DC,∠DCB=30度.求证:DC2+BC2=AC2,即四边形ABCD是勾股四边形.
【答案与解析】
一.选择题
1.【答案】D
【解析】判断一组数是不是勾股数时,应先判断他们是否都是正整数,在验证他们平方间的关系,所以只有D项满足.
2.【答案】B.
3.【答案】A;
【解析】由2n2+2n+1>2n2+2n,且2n2+2n+1>2n+1,得到2n2+2n+1为最长的边,
∵(2n+1)2+(2n2+2n)2=1+4n+8n2+8n3+4n4,(2n2+2n+1)2=1+4n+8n2+8n3+4n4
∴(2n+1)2+(2n2+2n)2=(2n2+2n+1)2∴△ABC为直角三角形.
4.【答案】C;
【解析】①c不一定是斜边,故错误;④若△ABC是直角三角形,c不是斜边,则(a+b)(a﹣b)≠c2,故错误.
5.【答案】C;
【解析】.
6.【答案】B;
【解析】因为,两边之和等于第三边,故不能组成一个三角形,①错误;因为,所以.又因为.得.两边同除以,得②正确;因为,所以③正确,360°×=150°,最大角并不是90°,所以④错误.
二.填空题
7.【答案】90°;
【解析】由题意,所以∠B=90°.
8.【答案】2;
【解析】由题意得:(x+1)2+(x+2)2=(x+3)2,解得:x1=2,x2=﹣2(不合题意,舍去).
9.【答案】24;
【解析】∵7<<9,∴=8.
10.【答案】13;直角三角形;
【解析】7<<17.
11.【答案】30;
【解析】解:由题意得:甲船的路程:AO=8×2=16,
乙船的路程:BO=15×2=30,
∵302+162=342,
∴∠AOB=90°,
∵AO是北偏东60°方向,
∴BO是南偏东30°.
故答案为:30.
12.【答案】能;
【解析】设为斜边,则,两边同乘以,得,即 .
三.解答题
13.【解析】
解:连接BD,
在Rt△ABD中,BD2=AB2+AD2=3002+4002=5002,
在△CBD中,CD2=13002,
BC2=12002,
而12002+5002=13002,
即BC2+BD2=CD2,
则∠DBC=90°,
S四边形ABCD=S△BAD+S△DBCAD?BD+BD?BC=360000m2.
答:种植草皮的面积是360000m2.
14.【解析】
(1)解:∵S=×3×4=6,
L=3+4+5=12,
∴==,
∴同理可得其他两空分别为1,;
(2);
证明:∵a+b﹣c=m,
∴a+b=m+c,
∴a2+2ab+b2=m2+2mc+c2,
又∵a2+b2=c2,
∴2ab=m2+2mc,
∴S==m(m+2c),
∴==.
15.【解析】
(1)解:正方形、长方形、直角梯形.(任选两个均可)
(2)解:答案如图所示.
(3)证明:连接EC,
∵△ABC≌△DBE,
∴AC=DE,BC=BE,
∵∠CBE=60°,
∴EC=BC,∠BCE=60°,
∵∠DCB=30°,
∴∠DCE=90°,
∴DC2+EC2=DE2,
∴DC2+BC2=AC2.
即四边形ABCD是勾股四边形.
【学习目标】
1. 理解勾股定理的逆定理,并能与勾股定理相区别;
2. 能运用勾股定理的逆定理判断一个三角形是否是直角三角形;
3. 理解勾股数的含义;
4. 通过探索直角三角形的判定条件的过程,培养动手操作能力和逻辑推理能力.
【要点梳理】
要点一、勾股定理的逆定理
如果三角形的三条边长,满足,那么这个三角形是直角三角形.
要点诠释:(1)勾股定理的逆定理的作用是判定某一个三角形是否是直角三角形.
(2)勾股定理的逆定理是把“数”转为“形”,是通过计算来判定一个三角形是否为直角三角形.
要点二、如何判定一个三角形是否是直角三角形
首先确定最大边(如).
验证与是否具有相等关系.若,则△ABC是∠C=90°的直角三角形;若,则△ABC不是直角三角形.
要点诠释:当时,此三角形为钝角三角形;当时,此三角形为锐角三角形,其中为三角形的最大边.
要点三、勾股数
满足不定方程的三个正整数,称为勾股数(又称为高数或毕达哥拉斯数),显然,以为三边长的三角形一定是直角三角形.
熟悉下列勾股数,对解题会很有帮助:
3、4、5; ②5、12、13;③8、15、17;④7、24、25;⑤9、40、41……
如果是勾股数,当为正整数时,以为三角形的三边长,此三角形必为直角三角形.
要点诠释:(1)(是自然数)是直角三角形的三条边长;
(2)(是自然数)是直角三角形的三条边长;
(3) (是自然数)是直角三角形的三条边长;
【典型例题】
类型一、勾股定理的逆定理
1、(2019春?咸丰县月考)如图所示,在△ABC中,AB:BC:CA=3:4:5,且周长为36cm,点P从点A开始沿AB边向B点以每秒1cm的速度移动;点Q从点B沿BC边向点C以每秒2cm的速度移动,如果同时出发,则过3秒时,△BPQ的面积为多少 cm2.
【思路点拨】本题先设适当的参数求出三角形的三边,由勾股定理的逆定理得出三角形为直角三角形.再求出3秒后的BP,BQ的长,利用三角形的面积公式计算求解.
【答案与解析】
解:设AB为3xcm,BC为4xcm,AC为5xcm,
∵周长为36cm,
AB+BC+AC=36cm,
∴3x+4x+5x=36,
得x=3,
∴AB=9cm,BC=12cm,AC=15cm,
∵AB2+BC2=AC2,
∴△ABC是直角三角形,
过3秒时,BP=9﹣3×1=6(cm),BQ=2×3=6(cm),
∴S△PBQ=BP?BQ=×(9﹣3)×6=18(cm2).
故过3秒时,△BPQ的面积为18cm2.
【总结升华】本题是道综合性较强的题,需要学生把勾股定理的逆定理、三角形的面积公式结合求解.由勾股定理的逆定理得出三角形为直角三角形,是解题的关键.隐含了整体的数学思想和正确运算的能力.
2、如图,点D是△ABC内一点,把△ABD绕点B顺时针方向旋转60°得到△CBE,若AD=4,BD=3,CD=5.
(1)判断△DEC的形状,并说明理由;
(2)求∠ADB的度数.
【思路点拨】把△ABD绕点B顺时针方向旋转60°,注意旋转只是三角形的位置变了,三角形的边长和角度并没有变,并且旋转的角度60°,因此出现等边△BDE,从而才能更有利的判断三角形的形状和求∠ADB的度数.
【答案与解析】
解:(1)根据图形的旋转不变性,
AD=EC,BD=BE,
又∵∠DBE=∠ABC=60°,
∴△ABC和△DBE均为等边三角形,
于是DE=BD=3,EC=AD=4,
又∵CD=5,
∴DE2+EC2=32+42=52=CD2;
故△DEC为直角三角形.
(2)∵△DEC为直角三角形,
∴∠DEC=90°,
又∵△BDE为等边三角形,
∴∠BED=60°,
∴∠BEC=90°+60°=150°,
即∠ADB=150°.
【总结升华】此题考查了旋转后图形的不变性、全等三角形的性质、等边三角形的性质、勾股定理的逆定理等知识,综合性较强,是一道好题.解答(2)时要注意运用(1)的结论.
举一反三:
【变式】如图所示,在△ABC中,已知∠ACB=90°,AC=BC,P是△ABC内一点,且PA=3,PB=1,PC=CD=2,CD⊥CP,求∠BPC的度数.
【答案】
解:连接BD.∵ CD⊥CP,且CD=CP=2,
∴ △CPD为等腰直角三角形,即∠CPD=45°.
∵ ∠ACP+∠BCP=∠BCP+∠BCD=90°,
∴ ∠ACP=∠BCD.
∵ CA=CB,
∴ △CAP≌△CBD(SAS),
∴ DB=PA=3.
在Rt△CPD中,.
又∵ PB=1,则.
∵ ,
∴ ,
∴ △DPB为直角三角形,且∠DPB=90°,
∴ ∠CPB=∠CPD+∠DPB=45°+90°=135°.
类型二、勾股定理逆定理的应用
3、已知a、b、c是△ABC的三边,且满足,且a+b+c=12,请你探索△ABC的形状.
【答案与解析】
解:令=k.
∴a+4=3k,b+3=2k,c+8=4k,
∴a=3k﹣4,b=2k﹣3,c=4k﹣8.
又∵a+b+c=12,
∴(3k﹣4)+(2k﹣3)+(4k﹣8)=12,
∴k=3.
∴a=5,b=3,c=4.
∴△ABC是直角三角形.
【总结升华】此题借用设比例系数k的方法,进一步求得三角形的三边长,根据勾股定理的逆定理判定三角形的形状.
举一反三:
【变式】(2018春?渝中区校级月考)△ABC的三边a、b、c满足|a+b﹣50|++(c﹣40)2=0.试判断△ABC的形状是 .
【答案】直角三角形.
解:∵|a+b﹣50|++(c﹣40)2=0,
∴,
解得,
∵92+402=412,
∴△ABC是直角三角形.
故答案为直角三角形.
4、如图所示,MN以左为我国领海,以右为公海,上午9时50分我国缉私艇A发现在其正东方向有一走私艇C并以每小时13海里的速度偷偷向我国领海开来,便立即通知距其5海里,并在MN线上巡逻的缉私艇B密切注意,并告知A和C两艇的距离是13海里,缉私艇B测得C与其距离为12海里,若走私艇C的速度不变,最早在什么时间进入我国海域?
【答案与解析】
解:∵ ,
∴ △ABC为直角三角形.∴ ∠ABC=90°.
又BD⊥AC,可设CD=,
∴
①-②得,
解得.∴ ≈0.85(h)=51(分).
所以走私艇最早在10时41分进入我国领海.
【总结升华】(1)本题用勾股定理作相等关系列方程解决问题,(2)用勾股定理的逆定理判定直角三角形,为勾股定理的运用提供了条件.
【巩固练习】
一.选择题
1.(2019春?平武县校级月考)下列各组数中,可以构成勾股数的是( )
A.13,16,19 B.,, C.18,24,36 D.12,35,37
2.(2018春?凉山州期末)△ABC中,∠A,∠B,∠C所对的边分别是a,b,c,满足下列条件的△ABC,不是直角三角形的是( )
A.a:b:c=1::1 B.∠A:∠B:∠C=3:4:5
C.(a+b)(a﹣b)=c D.∠A:∠B:∠C=1:2:3
3. 已知△ABC三边长分别为2n+1,2n2+2n,2n2+2n+1,(n为正整数),则△ABC为( )
A.
直角三角形
B.
等腰三角形
C.
锐角三角形
D.
钝角三角形
4. 有下面的判断:①△ABC中,a2+b2≠c2,则△ABC不是直角三角形.②△ABC是直角三角形,∠C=90°,则a2+b2=c2.③若△ABC中,a2﹣b2=c2,则△ABC是直角三角形.④若△ABC是直角三角形,则(a+b)(a﹣b)=c2.以上判断正确的有( )
A.
4个
B.
3个
C.
2个
D.
1个
5.五根小木棒,其长度分别为7,15,20,24,25,现将他们摆成两个直角三角形,其中正确的是( )
6. 为直角三角形的三边,且为斜边,为斜边上的高,下列说法:
①能组成一个三角形 ②能组成直角三角形
③能组成直角三角形 ④三个内角的度数之比为3:4:5能组成一个三角形
其中正确结论的个数是( )
A.1 B.2 C.3 D.4
二.填空题
7.若△ABC中,,则∠B=____________.
8.(2019春?罗定市期中)若△ABC的三边长分别为x+1,x+2,x+3,要使此三角形成为直角三角形,则x= .
9.若一个三角形的三边长分别为1、、8(其中为正整数),则以、、为边的三角形的面积为______.
10.△ABC的两边分别为5,12,另一边为奇数,且是3的倍数,则应为______,此三角形为______.
11.(2018春?寿县期中)在某港口有甲乙两艘渔船,若甲沿北偏东60°方向以每小时8海里的速度前进,同时,乙船沿南偏东角度以每小时15海里速度前进,2小时后,甲乙两船相距34海里,那么,乙船航行的方向是南偏东___________度.
12. 如果线段能组成一个直角三角形,那么________组成直角三角形.(填“能”或“不能”).
三.解答题
13.(2018秋?广州校级期末)如图,已知某经济开发区有一块四边形空地ABCD,现计划在该空地上种植草皮,经测量∠A=90°,AB=300m,AD=400m,CD=1300m,BC=1200m.请计算种植草皮的面积.
14.在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别是a、b、c.
(1)填表:
边a、b、c
三角形的面积与周长的比值
3 4 5
5 12 13
8 15 17
(2)若a+b﹣c=m,则猜想= (并证明此结论).
15. 我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.
(1)写出你所学过的特殊四边形中是勾股四边形的两种图形的名称正方形、长方形、直角梯形(任选两个均可);
(2)如图1,已知格点(小正方形的顶点)O(0,0),A(3,0),B(0,4),请你画出以格点为顶点,OA,OB为勾股边且对角线相等的勾股四边形OAMB;
(3)如图2,将△ABC绕顶点B按顺时针方向旋转60°,得到△DBE,连接AD,DC,∠DCB=30度.求证:DC2+BC2=AC2,即四边形ABCD是勾股四边形.
【答案与解析】
一.选择题
1.【答案】D
【解析】判断一组数是不是勾股数时,应先判断他们是否都是正整数,在验证他们平方间的关系,所以只有D项满足.
2.【答案】B.
3.【答案】A;
【解析】由2n2+2n+1>2n2+2n,且2n2+2n+1>2n+1,得到2n2+2n+1为最长的边,
∵(2n+1)2+(2n2+2n)2=1+4n+8n2+8n3+4n4,(2n2+2n+1)2=1+4n+8n2+8n3+4n4
∴(2n+1)2+(2n2+2n)2=(2n2+2n+1)2∴△ABC为直角三角形.
4.【答案】C;
【解析】①c不一定是斜边,故错误;④若△ABC是直角三角形,c不是斜边,则(a+b)(a﹣b)≠c2,故错误.
5.【答案】C;
【解析】.
6.【答案】B;
【解析】因为,两边之和等于第三边,故不能组成一个三角形,①错误;因为,所以.又因为.得.两边同除以,得②正确;因为,所以③正确,360°×=150°,最大角并不是90°,所以④错误.
二.填空题
7.【答案】90°;
【解析】由题意,所以∠B=90°.
8.【答案】2;
【解析】由题意得:(x+1)2+(x+2)2=(x+3)2,解得:x1=2,x2=﹣2(不合题意,舍去).
9.【答案】24;
【解析】∵7<<9,∴=8.
10.【答案】13;直角三角形;
【解析】7<<17.
11.【答案】30;
【解析】解:由题意得:甲船的路程:AO=8×2=16,
乙船的路程:BO=15×2=30,
∵302+162=342,
∴∠AOB=90°,
∵AO是北偏东60°方向,
∴BO是南偏东30°.
故答案为:30.
12.【答案】能;
【解析】设为斜边,则,两边同乘以,得,即 .
三.解答题
13.【解析】
解:连接BD,
在Rt△ABD中,BD2=AB2+AD2=3002+4002=5002,
在△CBD中,CD2=13002,
BC2=12002,
而12002+5002=13002,
即BC2+BD2=CD2,
则∠DBC=90°,
S四边形ABCD=S△BAD+S△DBCAD?BD+BD?BC=360000m2.
答:种植草皮的面积是360000m2.
14.【解析】
(1)解:∵S=×3×4=6,
L=3+4+5=12,
∴==,
∴同理可得其他两空分别为1,;
(2);
证明:∵a+b﹣c=m,
∴a+b=m+c,
∴a2+2ab+b2=m2+2mc+c2,
又∵a2+b2=c2,
∴2ab=m2+2mc,
∴S==m(m+2c),
∴==.
15.【解析】
(1)解:正方形、长方形、直角梯形.(任选两个均可)
(2)解:答案如图所示.
(3)证明:连接EC,
∵△ABC≌△DBE,
∴AC=DE,BC=BE,
∵∠CBE=60°,
∴EC=BC,∠BCE=60°,
∵∠DCB=30°,
∴∠DCE=90°,
∴DC2+EC2=DE2,
∴DC2+BC2=AC2.
即四边形ABCD是勾股四边形.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
