人教版高中数学必修二知识讲解,巩固练习(教学资料,补习资料):专题1.2.1、1.2.2 中心投影与平行投影、空间几何体的三视图
文档属性
| 名称 | 人教版高中数学必修二知识讲解,巩固练习(教学资料,补习资料):专题1.2.1、1.2.2 中心投影与平行投影、空间几何体的三视图 |  | |
| 格式 | zip | ||
| 文件大小 | 802.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-21 12:15:39 | ||
图片预览




文档简介
知识
一、中心投影与平行投影
1.投影的概念
由于光的照射,在不透明物体后面的屏幕上可以留下这个物体的影子,这种现象叫做 .其中,我们把光线叫做 ,把留下物体影子的屏幕叫做 .
2.中心投影
(1)概念
光由一点向外散射形成的投影,叫做 ,如图所示.现实生活中见到的很多投影都是中心投影,如在电灯泡、蜡烛等点光源照射下物体的影子.
(2)性质
①中心投影的投影线相交于 .
②平行于投影面放置的物体,点光源离物体越近,投影形成的影子越 .
例如,在电灯泡的照射下,物体后面的屏幕上会形成影子,而且随物体距离灯泡(或屏幕)的远近,形成的影子大小会有所不同.
3.平行投影
(1)概念
在一束平行光线照射下形成的投影,叫做 .在平行投影中,投影线正对着投影面时,叫做 ,否则叫做斜投影.如图所示. 在日常生活中,常常把太阳光线看作平行光线.
(2)性质
①平行投影的投影线互相 .
②在平行投影之下,与投影面平行的平面图形留下的影子,与这个平面图形的形状和大小是完全 的.
③当图形中的直线或线段不平行于投影线时:
(ⅰ)直线或线段的平行投影仍是 ;
(ⅱ)平行直线的平行投影是 的直线;
(ⅲ)平行于投影面的线段,它的投影与这条线段 ;
(ⅳ)与投影面平行的平面图形,它的投影与这个图形 ;
(ⅴ)在同一直线或平行直线上的两条线段的平行投影的长度比 这两条线段的长度比.
二、空间几何体的三视图
1.三视图的概念
(1)光线从几何体的前面向后面正投影,得到的投影图叫做几何体的 ;
(2)光线从几何体的左面向右面正投影,得到的投影图叫做几何体的 ;
(3)光线从几何体的上面向下面正投影,得到的投影图叫做几何体的 .
几何体的正视图、侧视图和俯视图统称为几何体的三视图.如图.
2.三视图的画法规则
(1)排列规则:一般地,侧视图在正视图的 ,俯视图在正视图的 .如下图:
正
侧
俯
(2)画法规则
①正视图与俯视图的长度一致,即“ ”;
②侧视图和正视图的高度一致,即“ ”;
③俯视图与侧视图的宽度一致,即“ ”.
(3)线条的规则
①能看见的轮廓线用 表示;
②不能看见的轮廓线用 表示.
3.常见几何体的三视图
常见几何体
正视图
侧视图
俯视图
长方体
矩形
矩形
矩形
正方体
正方形
正方形
正方形
圆柱
矩形
矩形
圆
圆锥
等腰三角形
等腰三角形
圆
圆台
等腰梯形
等腰梯形
两个同心的圆
球
圆
圆
圆
三、简单组合体的三视图
常见的组合体的生成方式:(1)将基本几何体拼接成的组合体;(2)从基本几何体中切掉或挖掉部分构成组合体.所以,在画组合体的三视图时,一定要认真观察,先认识它的基本结构,然后再画它的三视图.如图.
知识参考答案:
二、1.正视图 侧视图 俯视图
2.(1)右边 下边 (2)长对正 高平齐 宽相等 (3)实线 虚线
重点
重点:空间几何体的三视图.
难点:简单组合体的三视图、由三视图还原几何体.
易错:不能准确画出三视图或由三视图还原几何体.
1.K重点——空间几何体的三视图
正视图反映了物体上下、左右的位置关系,即反映了物体的高度和长度;侧视图反映了物体上下、前后的位置关系,即反映了物体的高度和宽度;俯视图反映了物体左右、前后的位置关系,即反映了物体的长度和宽度.
下列几何体各自的三视图中,有且仅有两个视图相同的是
A.①② B.①③
C.①④ D.②④
【答案】D
【解析】②中正视图和侧视图相同,④中正视图和侧视图相同,可得②④正确,故选D.
【名师点睛】在确定几何体的三视图时可以按照下面的步骤进行:确定投影角度→按照三视图的画法规则作图→完成后检验.
2.K难点——简单组合体的三视图
对于简单组合体要分清楚是由哪些简单几何体组成的,并注意它们的组合方式,特别是它们的交线位置,画出分解后的简单几何体的三视图后,将其拼合即得组合体的三视图.
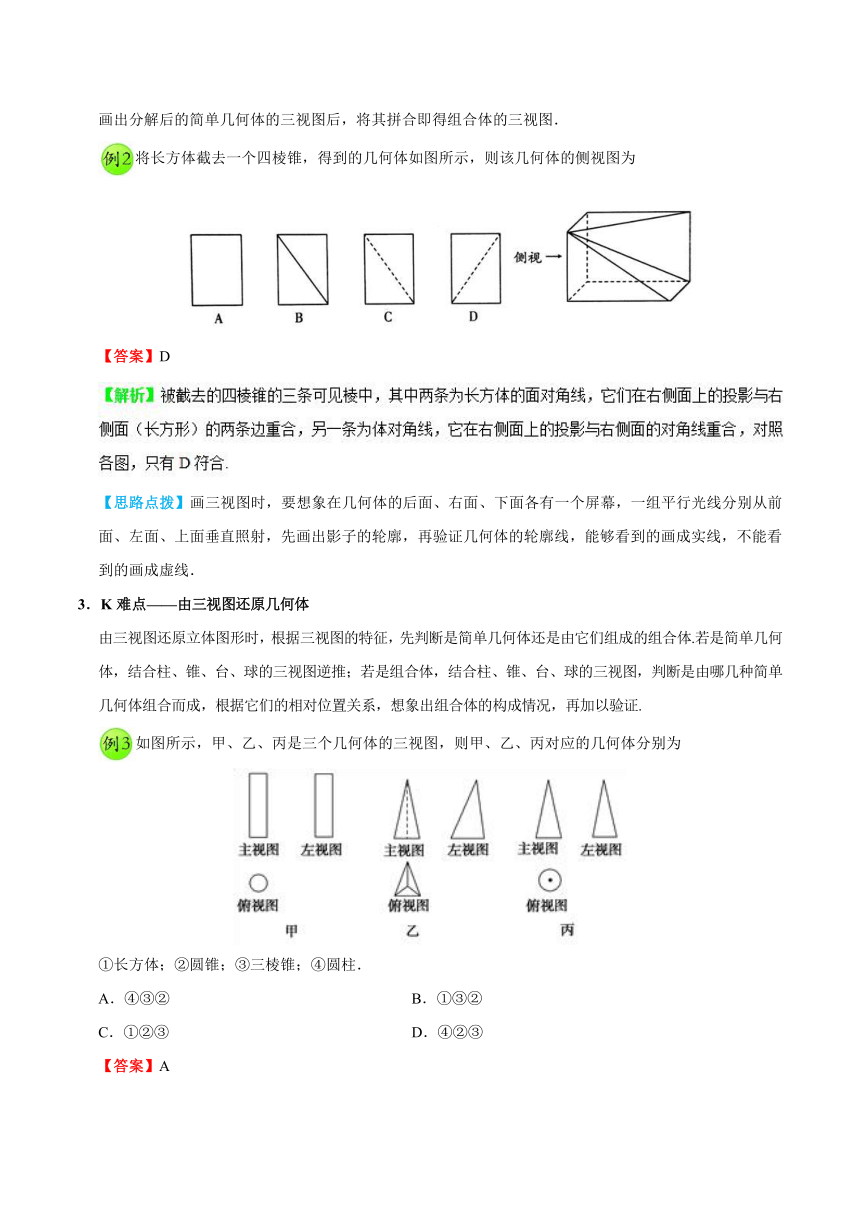
将长方体截去一个四棱锥,得到的几何体如图所示,则该几何体的侧视图为
【答案】D
【思路点拨】画三视图时,要想象在几何体的后面、右面、下面各有一个屏幕,一组平行光线分别从前面、左面、上面垂直照射,先画出影子的轮廓,再验证几何体的轮廓线,能够看到的画成实线,不能看到的画成虚线.
3.K难点——由三视图还原几何体
由三视图还原立体图形时,根据三视图的特征,先判断是简单几何体还是由它们组成的组合体.若是简单几何体,结合柱、锥、台、球的三视图逆推;若是组合体,结合柱、锥、台、球的三视图,判断是由哪几种简单几何体组合而成,根据它们的相对位置关系,想象出组合体的构成情况,再加以验证.
如图所示,甲、乙、丙是三个几何体的三视图,则甲、乙、丙对应的几何体分别为
①长方体;②圆锥;③三棱锥;④圆柱.
A.④③② B.①③②
C.①②③ D.④②③
【答案】A
【技巧点拨】由三视图判断几何体时,首先,确定正视、侧视、俯视的方向;其次,判断几何体的组合方式,特别是它们的交线位置,交线的实虚情况等.要注意不能看见的轮廓线的画法,应画成虚线,切不可略去不画.
4.K易错——不能准确由三视图还原几何体
当已知三视图去还原成几何体时,要充分关注图形中关键点的投影,先从俯视图来确定是多面体还是旋转体,再从正视图和侧视图想象出几何体的大致形状,然后通过已知的三视图验证几何体的正确性,最后检查轮廓线的实虚.
一个几何体的三视图如图所示,则该几何体的直观图可以是
【错解】A或B或C
【错因分析】选A,俯视图判断出错,从俯视图看,几何体的上、下部分都是旋转体;选B,下部分几何体判断出错,误把旋转体当多面体;选C,上部分几何体判断出错,误把旋转体当多面体.
【正解】由三视图可知该几何体上部是一个圆台,下部是一个圆柱,选D.
基础训练
1.下列各项中,不属于三视图的是
A.正视图 B.侧视图
C.后视图 D.俯视图
2.下列光线所形成的投影,不是中心投影的是
A.太阳光线 B.台灯的光线
C.手电筒的光线 D.路灯的光线
3.两条相交直线的平行投影是
A.两条相交直线 B.一条直线
C.两条平行直线 D.两条相交直线或一条直线
4.下列几何体中,正视图、侧视图和俯视图都相同的是
A.圆柱 B.圆锥
C.球 D.三棱锥
5.若一个几何体的三视图如下图所示,则这个几何体是
A.三棱锥 B.四棱锥
C.三棱柱 D.四棱柱
6.沿圆柱体上底面直径截去一部分后的物体如图所示,它的俯视图是
A. B.
C. D.
7.如下图为长方体木块堆成的几何体的三视图,则组成此几何体的长方体木块块数共有
A.3块 B.4块
C.5块 D.6块
8.如图所示,画出四面体AB1CD1三视图中的正视图,以面AA1D1D为投影面,则得到的正视图可以为
A. B.
C. D.
9.给出以下结论,其中正确的结论的序号是________.
①一个点光源把一个平面图形照射到一个平面上,它的投影与这个图形全等;
②平行于投射面的平面图形,在平行投影下,它的投影与原图形全等;
③垂直于投射面的平面图形,在平行投影下,它的投影与原图形相似;
④在平行投影下,不平行、也不垂直于投射面的线段的投影仍是线段,但与原线段不等长.
10.桌子上放着一个长方体和一个圆柱(如图所示),则下列三幅图分别是什么图(填“正视图、俯视图、侧视图”).①________、②________、③________.
11.如图所示,是一个长方体截去一个角所得多面体的直观图和它的主视图、左视图(单位:).请在正视图下面,按照画三视图的要求画出该多面体的俯视图.
能力提升
12.当图形中的直线或线段不平行于投影线时,关于平行投影的性质,下列说法不正确的是
A.直线或线段的平行投影仍是直线或线段
B.平行直线的平行投影仍是平行的直线
C.与投射面平行的平面图形,它的投影与这个图形全等
D.在同一直线或平行直线上,两条线段平行投影的比等于这两条线段的比
13.已知三棱锥的正视图与俯视图如图所示,俯视图是边长为2的正三角形,则该三棱锥的侧视图可能为
A. B.
C. D.
14.“牟合方盖”是我国古代数学家刘徽在研究球的体积的过程中构造的一个和谐优美的几何体.它由完全相同的四个曲面构成,相对的两个曲面在同一个圆柱的侧面上,好似两个扣合(牟合)在一起的方形伞(方盖),其直观图如下图,图中四边形是为体现其直观性所作的辅助线.当其正视图和侧视图完全相同时,它的俯视图可能是
15.如图为某组合体的三视图,则俯视图中的长和宽分别为
A. B.
C. D.
16.在棱长为1的正方体中,若分别为的中点,则空间四边形在正方体下底面上的射影面积为
A.1 B.
C. D.
17.一个几何体的三视图如图所示,其中正视图是边长为的正三角形,俯视图是正方形,那么该几何体的侧视图的面积是________.
真题练习
18.(2018年高考新课标I卷)某圆柱的高为2,底面周长为16,其三视图如图.圆柱表面上的点在正视图上的对应点为,圆柱表面上的点在左视图上的对应点为,则在此圆柱侧面上,从到的路径中,最短路径的长度为
A. B.
C.3 D.2
19.(2018年高考新课标Ⅲ卷文)中国古建筑借助榫卯将木构件连接起来,构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是
20.(2018年高考北京卷文)某四棱锥的三视图如图所示,在此四棱锥的侧面中,直角三角形的个数为
A.1 B.2
C.3 D.4
21.(2019山东模拟)某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形.该多面体的各个面中有若干个是梯形,这些梯形的面积之和为
A.10 B.12
C.14 D.16
22.(2019年高考北京模拟)某四棱锥的三视图如图所示,则该四棱锥的最长棱的长度为
A.3 B.2
C.2 D.2
23.(2019年高考天津模拟)将一个长方体沿相邻三个面的对角线截去一个棱锥,得到的几何体的正视图与俯视图如图所示,则该几何体的侧(左)视图为
A B C D
参考答案
1
2
3
4
5
6
7
8
12
13
14
15
16
18
19
20
21
22
23
C
A
D
C
B
D
B
A
B
B
B
A
B
B
A
C
B
B
B
1.【答案】C
【解析】根据三视图的规定可知,后视图不属于三视图.
2.【答案】A
【解析】太阳光线形成的投影是平行投影.
3.【答案】D
4.【答案】C
【解析】由题意得,球的三视图都是圆,所以正视图、侧视图和俯视图都相同的是球,故选C.
5.【答案】B
【解析】由俯视图可知底面为四边形,由正视图和侧视图知侧面为三角形,故几何体为四棱锥.
本题选择B选项.
【名师点睛】空间几何体的三视图是从空间几何体的正面、左面、上面用平行投影的方法得到的三个平面投影图.因此在分析空间几何体的三视图问题时,就要抓住正投影,结合具体问题和空间几何体的结构特征进行解答.
6.【答案】D
【解析】从上面看依然可得到两个半圆的组合图形,注意看得到的棱画实线.
7.【答案】B
【解析】由三视图可知组成此几何体的长方体木块共摆放两层,下层三块,上层一块,如图,设四边形是长方形的直观图,在下层的处各放一块,上层的一块在的正上方,共块,故选B.
8.【答案】A
【解析】显然AB1、AC、B1D1、CD1分别投影得到正视图的外轮廓,B1C为可见实线,AD1为不可见虚线.本题选择A选项.
【名师点睛】三视图画法:
(1)实、虚线的画法:分界线和可见轮廓线用实线,看不见的轮廓线用虚线;
(2)理解“长对正、高平齐、宽相等”.
9.【答案】②④
【解析】由定义知,②④正确.
10.【答案】俯视图 正视图 侧视图
【解析】由三视图的定义可知,①是俯视图,②是正视图,③是侧视图.
11.【答案】俯视图见解析.
【解析】依据三视图的绘图原则,可作出该几何体的俯视图如图.
12.【答案】B
13.【答案】B
【解析】由正视图和俯视图还原几何体如图所示,由正视图和俯视图对应线段可得,当点C在面ABD上的射影是B时,,的边上的高为,只有B选项符合,当点C在面ABD上的射影不是B时,没有符合条件的选项,故选B.
【名师点睛】(1)解答此类题目的关键是由多面体的三视图想象出空间几何体的形状并画出其直观图.
(2)三视图中“正侧一样高、正俯一样长、俯侧一样宽”,因此,可以根据三视图的形状及相关数据推断出原几何图形中的点、线、面之间的位置关系及相关数据.
14.【答案】B
15.【答案】A
【解析】由三视图可知,俯视图的长可由主视图得到,即,俯视图的宽可由左视图得到,即,故选A.
16.【答案】B
【解析】设边DC的中点为H,由题意可得,点E,F,B,G在底面上的射影分别为点H,A,B,B,因此空间四边形在正方体下底面上的射影为,其面积为.选B.
17.【答案】
【解析】由三视图复原的几何体的底面为正方形(边长为2),正视图是正三角形,所以几何体是正四棱锥,侧视图与正视图图形相同,侧视图是边长为2的正三角形,所以侧视图的面积为,故答案为.
18.【答案】B
【解析】根据圆柱的三视图以及其本身的特征,可以确定点M和点N分别在以圆柱的高为长方形的宽,圆柱底面圆周长的四分之一为长的长方形的对角线的端点处,所以所求的最短路径的长度为,故选B.
【名师点睛】该题考查的是有关几何体的表面上两点之间的最短距离的求解问题,在解题的过程中,需要明确两个点在几何体上所处的位置,再利用平面上两点间直线段最短,所以处理方法就是将面切开平铺,利用平面图形的相关特征求得结果.解本题时,首先根据题中所给的三视图,得到点M和点N在圆柱上所处的位置,点M在上底面上,点N在下底面上,并且将圆柱的侧面展开图平铺,点M、N在其四分之一的矩形的对角线的端点处,根据平面上两点间直线段最短,利用勾股定理,求得结果.
19.【答案】A
【解析】观察图形图可知,俯视图为,故答案为A.
【名师点睛】本题主要考查空间几何体的三视图,考查学生的空间想象能力,属于基础题.
20.【答案】C
21.【答案】B
【解析】由题意该几何体的直观图是由一个三棱锥和三棱柱构成,如下图,则该几何体各面内只有两个相同的梯形,则这些梯形的面积之和为,故选B.
【名师点睛】三视图往往与几何体的体积、表面积以及空间线面关系、角、距离等问题相结合,解决此类问题的关键是由三视图准确确定空间几何体的形状及其结构特征并且熟悉常见几何体的三视图.
22.【答案】B
【解析】几何体是四棱锥,如图.
【名师点睛】本题考查了空间想象能力,由三视图还原几何体的方法:
或者也可根据三视图的形状,将几何体的顶点放在正方体或长方体里面,便于分析问题.
23.【答案】B
【解析】由题意得截去的是长方体前右上方顶点处的一个棱锥,故选B.
【名师点睛】(1)解答此类题目的关键是由多面体的三视图想象出空间几何体的形状并画出其直观图.
(2)三视图中“正侧一样高、正俯一样长、俯侧一样宽”,因此,可以根据三视图的形状及相关数据推断出原几何体中的点、线、面之间的位置关系及相关数据.
