高中数学新人教B版必修5课件:第二章数列2.3.2等比数列的前n项和(33张)
文档属性
| 名称 | 高中数学新人教B版必修5课件:第二章数列2.3.2等比数列的前n项和(33张) |

|
|
| 格式 | zip | ||
| 文件大小 | 850.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-21 12:51:12 | ||
图片预览











文档简介
课件33张PPT。2.3.2 等比数列的前n项和1.理解等比数列前n项和公式的推导过程.
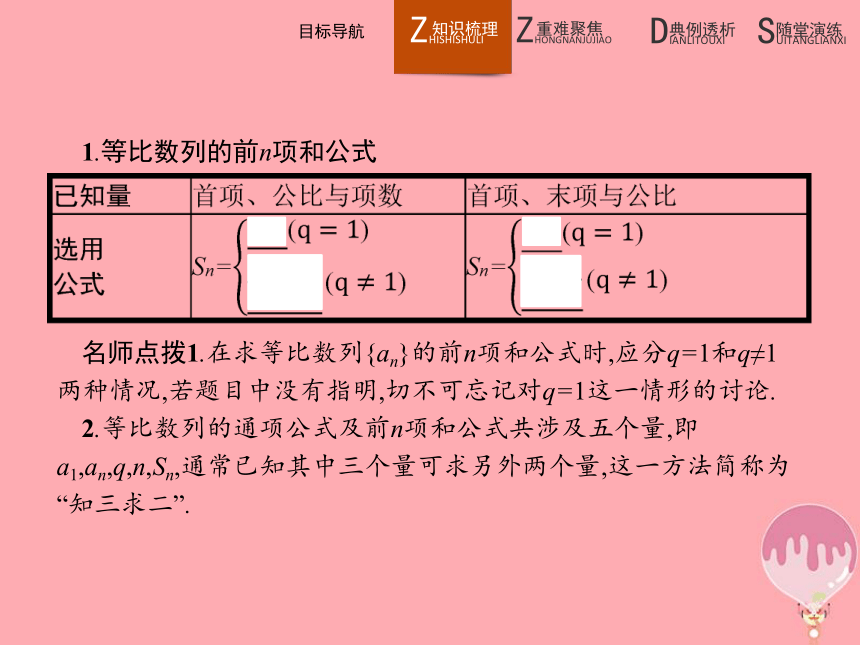
2.掌握等比数列的前n项和公式,并能用它解决有关等比数列问题.1.等比数列的前n项和公式 名师点拨1.在求等比数列{an}的前n项和公式时,应分q=1和q≠1两种情况,若题目中没有指明,切不可忘记对q=1这一情形的讨论.
2.等比数列的通项公式及前n项和公式共涉及五个量,即a1,an,q,n,Sn,通常已知其中三个量可求另外两个量,这一方法简称为“知三求二”.【做一做1-1】 在等比数列{an}中,已知公比q=-2,S5=44,则a1的值为( )
A.4 B.-4
C.2 D.-2
解析:由题意,知q≠1,故有S5=44= .将q=-2代入解得a1=4.
答案:A
【做一做1-2】 若等比数列{an}满足a2+a4=20,a3+a5=40,则公比q= ;前n项和Sn= .?
解析:根据等比数列的性质,得a3+a5=q(a2+a4),
所以q=2.又a2+a4=a1q+a1q3,故求得a1=2,
所以Sn= =2n+1-2.
答案:2 2n+1-22.等比数列前n项和的常用性质
(1)在公比为q(q≠-1)的等比数列{an}中,若Sn为其前n项和,则依次每k项的和构成等比数列,即Sk,S2k-Sk,S3k-S2k,S4k-S3k,…成等比数列,其公比为qk .
(2)在等比数列{an}中,若项数为2n,公比为q,奇数项之和为S奇,偶数项之和为S偶,则 =q .
(3)数列{an}是公比为q的等比数列,则Sm+n=Sn+qn·Sm .
【做一做2】 已知等比数列{an},Sn是其前n项和,且S3=7,S6=63,则S9= .?
答案:511一二三一、错位相减法的实质及应用
剖析:(1)用错位相减法求等比数列前n项和的实质是把等式两边同乘公比q,得一新的等式,错位相减求出Sn-qSn,这样可以消去大量的“中间项”,从而能求出Sn.当q=1时, Sn=na1,当q≠1时,Sn= .这是分段函数的形式,分段的界限是q=1.
(2)对于形如{xnyn}的数列的和,其中数列{xn}为等差数列,数列{yn}为等比数列,可以用错位相减法求和.错位相减法实际上是把一个数列的求和问题转化为等比数列的求和问题.
(3)利用这种方法时,要注意对公比的分类讨论.一二三二、等比数列的前n项和公式的推导(首项为a1,公比q≠1)
剖析:除了书上用到的错位相减法之外,还有以下方法可以求等比数列的前n项和.
(1)等比性质法一二三(2)拆项法
Sn=a1+a2+a3+…+an
=a1+a1q+a1q2+…+a1qn-1
=a1+q(a1+a1q+a1q2+…+a1qn-2)
=a1+q(a1+a1q+a1q2+…+a1qn-2+a1qn-1-a1qn-1),
∴Sn=a1+q(Sn-a1qn-1)
=a1+q(Sn-an).一二三三、教材中的“?”
例2有别的解法吗?将这个数列的前8项倒过来排,试一试.
剖析:∵S8=27+26+25+…+2+1,∴S8=1+2+22+…+26+27= =28-1=255.
此题说明在等比数列{an}中,若为有限项,如a1,a2,…,an,则an,an-1,…,a2,a1也是等比数列,其公比为原数列公比的倒数.题型一题型二题型三题型四题型五等比数列的前n项和公式的应用
【例1】 在等比数列{an}中,
(1)已知a1=3,q=2,求a6,S6;
(2)已知a1=-1,a4=64,求q和S4;分析:在等比数列的前n项和公式中有五个基本量a1,an,q,n,Sn,只要已知任意三个,就可以求出其他两个.题型一题型二题型三题型四题型五反思在等比数列{an}中,首项a1与公比q是两个最基本的元素;有关等比数列的问题,均可化成关于a1,q的方程或方程组来求解.解题过程中,要注意:(1)选择适当的公式;(2)灵活运用等比数列的有关性质;(3)在使用等比数列前n项和公式时,要考虑q是否等于1.题型一题型二题型三题型四题型五【变式训练1】 在等比数列{an}中,
(1)若Sn=189,q=2,an=96,求a1和n;
(2)若a1+a3=10,a4+a6= ,求a4和S5;
(3)若q=2,S4=1,求S8.题型一题型二题型三题型四题型五题型一题型二题型三题型四题型五题型一题型二题型四题型五题型三等比数列前n项和性质的应用
【例2】 在各项均为正数的等比数列{an}中,若S10=10,S20=30,求S30.
分析:可以利用解方程组解决,也可以利用等比数列的前n项和的性质来解决.题型一题型二题型四题型五题型三方法二:由性质Sm+n=Sn+qn·Sm,
得S20=S10+q10S10,
即30=10+10q10,
所以q10=2.
所以S30=S20+q20S10=30+40=70.
方法三:运用性质Sk,S2k-Sk,S3k-S2k,S4k-S3k,…成等比数列.
因为S10,S20-S10,S30-S20成等比数列,而S10=10,S20=30,
所以(S20-S10)2=S10·(S30-S20),
即(30-10)2=10×(S30-30).所以S30=70.
反思由于等比数列中,无论是通项公式还是前n项和公式,均与q的若干次幂有关,所以在解决等比数列问题时,经常出现高次方程,为达到降幂的目的,在解方程组时经常利用两式相除,达到整体消元的目的.题型一题型二题型四题型五题型三【变式训练2】 已知一个等比数列的首项为1,项数是偶数,其奇数项之和为85,偶数项之和为170,则这个数列的公比q= ,项数n= .?解析:方法一:设该等比数列的公比为q,项数为2n,
则有S偶=q·S奇,∴22n-1=255,
∴2n=8,
故这个数列的公比为2,项数为8.题型一题型二题型四题型五题型三方法二:设该等比数列的公比为q,项数为2n,
则奇数项和偶数项也分别成等比数列,公比均为q2.∴q=2,n=4,
∴这个数列的公比为2,项数为8.
答案:2 8题型一题型二题型三题型四题型五某些特殊数列的求和
【例3】 (1)已知数列{an}的通项公式an=2n+n,求该数列的前n项和Sn;
(2)已知数列{an}的通项公式an=n·2n,求该数列的前n项和Sn.
分析:(1)所给数列虽然不是等差数列或等比数列,但在求该数列的前n项和时可以把an看成一个等比数列和一个等差数列的和的形式,分别求和,再相加.(2)写出数列的前n项和,注意其与等比数列形式类似,考虑用推导等比数列求和公式的方法来求其前n项和.
解:(1)Sn=a1+a2+a3+…+an
=(2+1)+(22+2)+(23+3)+…+(2n+n)
=(2+22+23+…+2n)+(1+2+3+…+n)题型一题型二题型三题型四题型五(2)∵Sn=1×21+2×22+3×23+…+n·2n,
2Sn=1×22+2×23+…+(n-1)·2n+n·2n+1,
∴-Sn=2+22+23+…+2n-n·2n+1,
∴Sn=n·2n+1-(2+22+23+…+2n)=n·2n+1-(2n+1-2)
=(n-1)·2n+1+2.
反思1.分组求和法适用于某些特殊数列的求和,这些特殊数列的通项可写成几个等比数列或等差数列的和的形式.
2.错位相减法适用于求一个等差数列与一个等比数列的积组成的新数列的前n项和.题型一题型二题型三题型四题型五【变式训练3】 已知Sn=1+a+a2+…+an,求Sn.题型一题型二题型三题型四题型五等比数列前n项和的实际应用
【例4】 为了保护某处珍贵文物古迹,政府决定建一堵大理石护墙,设计时,为了与周边景观协调,对于同种规格的大理石用量须按下述法则计算:第一层用全部大理石的一半多一块,第二层用剩下的一半多一块,依此类推,到第十层恰好将大理石用完.已知大理石有偶数块,问共需大理石多少块?每层各用大理石多少块?
分析:设共用大理石的块数,即可列出各层大理石的使用块数,通过观察,此为一等比数列,通过等比数列求和,求出总块数,再求出每层用的块数.题型一题型二题型三题型四题型五解:设共用大理石x块,x为偶数,则各层用大理石块数分别为 答:共用去大理石2 046块,各层分别为1 024,512,256,128,64,32,16,8,4,2块.题型一题型二题型三题型四题型五反思对于实际问题,可以采用设出未知量的方法使之具体化.通过对前几项的探求,寻找其为等比数列的本质,再通过等比数列求和公式来求解.题型一题型二题型三题型四题型五【变式训练4】 从社会效益和经济效益出发,某地投入资金进行生态环境建设,并以此发展旅游产业,根据规划,本年度投入800万元,以后每年的投入将比上年减少 ,本年度当地旅游业收入估计为400万元,由于该项建设对旅游业的促进作用,预计今后旅游业收入每年会比上年增加 .设n年内(本年度为第1年)总投入Sn万元,旅游业总收入为Tn万元,写出Sn,Tn的表达式.
分析:根据题意可知投入资金及收入资金分别成等比数列,列出投入资金和收入资金的通项公式,再利用等比数列的求和公式求解.题型一题型二题型三题型四题型五题型四题型五题型一题型二题型三易错辨析
易错点:忽视对项数的分类讨论而致误
【例5】 已知数列{an}满足 试求其前n项和.
错解:Sn=a1+a2+a3+…+an
=(a1+a3+a5+…+an-1)+(a2+a4+a6+…+an)错因分析:这里数列的通项an是关于n的分段函数,当n为奇数或为偶数时对应不同的法则,因此求和时必须对项数n进行分类讨论.题型四题型五题型一题型二题型三1 2 3 4 51已知数列{an}满足3an+1+an=0,a2=- ,则数列{an}的前10项和等于( )
A.-6(1-3-10) B. (1-310)
C.3(1-3-10) D.3(1+3-10)答案:C 1 2 3 4 5?1 2 3 4 53某人为了观看2018年世界杯,从2011年起,每年5月10日到银行存入a元定期储蓄,若年利率为p,且保持不变,并约定每年到期存款均自动转为新的一年定期,到2018年将所有的存款及利息全部取回,则可取回的总钱数为( )元.
A.a(1+p)7 B.a(1+p)8
解析:2011年存入的a元到2018年所得的本息和为a(1+p)7,2012年存入的a元到2018年所得的本息和为a(1+p)6,依此类推,则2017年存入的a元到2018年的本息和为a(1+p),每年所得的本息和构成一个以a(1+p)为首项,1+p为公比的等比数列,则到2018年取回的总额为a(1+p)+a(1+p)2+…+a(1+p)7=
答案:D4在等比数列{an}中,已知Sn=65,n=4,q= ,则a1= .? 1 2 3 4 5答案:27 1 2 3 4 55设数列{an}满足:a1=1,an+1=3an,n∈N+.
(1)求{an}的通项公式及前n项和Sn;
(2)已知{bn}是等差数列,Tn为其前n项和,且b1=a2,b3=a1+a2+a3,求T20.
2.掌握等比数列的前n项和公式,并能用它解决有关等比数列问题.1.等比数列的前n项和公式 名师点拨1.在求等比数列{an}的前n项和公式时,应分q=1和q≠1两种情况,若题目中没有指明,切不可忘记对q=1这一情形的讨论.
2.等比数列的通项公式及前n项和公式共涉及五个量,即a1,an,q,n,Sn,通常已知其中三个量可求另外两个量,这一方法简称为“知三求二”.【做一做1-1】 在等比数列{an}中,已知公比q=-2,S5=44,则a1的值为( )
A.4 B.-4
C.2 D.-2
解析:由题意,知q≠1,故有S5=44= .将q=-2代入解得a1=4.
答案:A
【做一做1-2】 若等比数列{an}满足a2+a4=20,a3+a5=40,则公比q= ;前n项和Sn= .?
解析:根据等比数列的性质,得a3+a5=q(a2+a4),
所以q=2.又a2+a4=a1q+a1q3,故求得a1=2,
所以Sn= =2n+1-2.
答案:2 2n+1-22.等比数列前n项和的常用性质
(1)在公比为q(q≠-1)的等比数列{an}中,若Sn为其前n项和,则依次每k项的和构成等比数列,即Sk,S2k-Sk,S3k-S2k,S4k-S3k,…成等比数列,其公比为qk .
(2)在等比数列{an}中,若项数为2n,公比为q,奇数项之和为S奇,偶数项之和为S偶,则 =q .
(3)数列{an}是公比为q的等比数列,则Sm+n=Sn+qn·Sm .
【做一做2】 已知等比数列{an},Sn是其前n项和,且S3=7,S6=63,则S9= .?
答案:511一二三一、错位相减法的实质及应用
剖析:(1)用错位相减法求等比数列前n项和的实质是把等式两边同乘公比q,得一新的等式,错位相减求出Sn-qSn,这样可以消去大量的“中间项”,从而能求出Sn.当q=1时, Sn=na1,当q≠1时,Sn= .这是分段函数的形式,分段的界限是q=1.
(2)对于形如{xnyn}的数列的和,其中数列{xn}为等差数列,数列{yn}为等比数列,可以用错位相减法求和.错位相减法实际上是把一个数列的求和问题转化为等比数列的求和问题.
(3)利用这种方法时,要注意对公比的分类讨论.一二三二、等比数列的前n项和公式的推导(首项为a1,公比q≠1)
剖析:除了书上用到的错位相减法之外,还有以下方法可以求等比数列的前n项和.
(1)等比性质法一二三(2)拆项法
Sn=a1+a2+a3+…+an
=a1+a1q+a1q2+…+a1qn-1
=a1+q(a1+a1q+a1q2+…+a1qn-2)
=a1+q(a1+a1q+a1q2+…+a1qn-2+a1qn-1-a1qn-1),
∴Sn=a1+q(Sn-a1qn-1)
=a1+q(Sn-an).一二三三、教材中的“?”
例2有别的解法吗?将这个数列的前8项倒过来排,试一试.
剖析:∵S8=27+26+25+…+2+1,∴S8=1+2+22+…+26+27= =28-1=255.
此题说明在等比数列{an}中,若为有限项,如a1,a2,…,an,则an,an-1,…,a2,a1也是等比数列,其公比为原数列公比的倒数.题型一题型二题型三题型四题型五等比数列的前n项和公式的应用
【例1】 在等比数列{an}中,
(1)已知a1=3,q=2,求a6,S6;
(2)已知a1=-1,a4=64,求q和S4;分析:在等比数列的前n项和公式中有五个基本量a1,an,q,n,Sn,只要已知任意三个,就可以求出其他两个.题型一题型二题型三题型四题型五反思在等比数列{an}中,首项a1与公比q是两个最基本的元素;有关等比数列的问题,均可化成关于a1,q的方程或方程组来求解.解题过程中,要注意:(1)选择适当的公式;(2)灵活运用等比数列的有关性质;(3)在使用等比数列前n项和公式时,要考虑q是否等于1.题型一题型二题型三题型四题型五【变式训练1】 在等比数列{an}中,
(1)若Sn=189,q=2,an=96,求a1和n;
(2)若a1+a3=10,a4+a6= ,求a4和S5;
(3)若q=2,S4=1,求S8.题型一题型二题型三题型四题型五题型一题型二题型三题型四题型五题型一题型二题型四题型五题型三等比数列前n项和性质的应用
【例2】 在各项均为正数的等比数列{an}中,若S10=10,S20=30,求S30.
分析:可以利用解方程组解决,也可以利用等比数列的前n项和的性质来解决.题型一题型二题型四题型五题型三方法二:由性质Sm+n=Sn+qn·Sm,
得S20=S10+q10S10,
即30=10+10q10,
所以q10=2.
所以S30=S20+q20S10=30+40=70.
方法三:运用性质Sk,S2k-Sk,S3k-S2k,S4k-S3k,…成等比数列.
因为S10,S20-S10,S30-S20成等比数列,而S10=10,S20=30,
所以(S20-S10)2=S10·(S30-S20),
即(30-10)2=10×(S30-30).所以S30=70.
反思由于等比数列中,无论是通项公式还是前n项和公式,均与q的若干次幂有关,所以在解决等比数列问题时,经常出现高次方程,为达到降幂的目的,在解方程组时经常利用两式相除,达到整体消元的目的.题型一题型二题型四题型五题型三【变式训练2】 已知一个等比数列的首项为1,项数是偶数,其奇数项之和为85,偶数项之和为170,则这个数列的公比q= ,项数n= .?解析:方法一:设该等比数列的公比为q,项数为2n,
则有S偶=q·S奇,∴22n-1=255,
∴2n=8,
故这个数列的公比为2,项数为8.题型一题型二题型四题型五题型三方法二:设该等比数列的公比为q,项数为2n,
则奇数项和偶数项也分别成等比数列,公比均为q2.∴q=2,n=4,
∴这个数列的公比为2,项数为8.
答案:2 8题型一题型二题型三题型四题型五某些特殊数列的求和
【例3】 (1)已知数列{an}的通项公式an=2n+n,求该数列的前n项和Sn;
(2)已知数列{an}的通项公式an=n·2n,求该数列的前n项和Sn.
分析:(1)所给数列虽然不是等差数列或等比数列,但在求该数列的前n项和时可以把an看成一个等比数列和一个等差数列的和的形式,分别求和,再相加.(2)写出数列的前n项和,注意其与等比数列形式类似,考虑用推导等比数列求和公式的方法来求其前n项和.
解:(1)Sn=a1+a2+a3+…+an
=(2+1)+(22+2)+(23+3)+…+(2n+n)
=(2+22+23+…+2n)+(1+2+3+…+n)题型一题型二题型三题型四题型五(2)∵Sn=1×21+2×22+3×23+…+n·2n,
2Sn=1×22+2×23+…+(n-1)·2n+n·2n+1,
∴-Sn=2+22+23+…+2n-n·2n+1,
∴Sn=n·2n+1-(2+22+23+…+2n)=n·2n+1-(2n+1-2)
=(n-1)·2n+1+2.
反思1.分组求和法适用于某些特殊数列的求和,这些特殊数列的通项可写成几个等比数列或等差数列的和的形式.
2.错位相减法适用于求一个等差数列与一个等比数列的积组成的新数列的前n项和.题型一题型二题型三题型四题型五【变式训练3】 已知Sn=1+a+a2+…+an,求Sn.题型一题型二题型三题型四题型五等比数列前n项和的实际应用
【例4】 为了保护某处珍贵文物古迹,政府决定建一堵大理石护墙,设计时,为了与周边景观协调,对于同种规格的大理石用量须按下述法则计算:第一层用全部大理石的一半多一块,第二层用剩下的一半多一块,依此类推,到第十层恰好将大理石用完.已知大理石有偶数块,问共需大理石多少块?每层各用大理石多少块?
分析:设共用大理石的块数,即可列出各层大理石的使用块数,通过观察,此为一等比数列,通过等比数列求和,求出总块数,再求出每层用的块数.题型一题型二题型三题型四题型五解:设共用大理石x块,x为偶数,则各层用大理石块数分别为 答:共用去大理石2 046块,各层分别为1 024,512,256,128,64,32,16,8,4,2块.题型一题型二题型三题型四题型五反思对于实际问题,可以采用设出未知量的方法使之具体化.通过对前几项的探求,寻找其为等比数列的本质,再通过等比数列求和公式来求解.题型一题型二题型三题型四题型五【变式训练4】 从社会效益和经济效益出发,某地投入资金进行生态环境建设,并以此发展旅游产业,根据规划,本年度投入800万元,以后每年的投入将比上年减少 ,本年度当地旅游业收入估计为400万元,由于该项建设对旅游业的促进作用,预计今后旅游业收入每年会比上年增加 .设n年内(本年度为第1年)总投入Sn万元,旅游业总收入为Tn万元,写出Sn,Tn的表达式.
分析:根据题意可知投入资金及收入资金分别成等比数列,列出投入资金和收入资金的通项公式,再利用等比数列的求和公式求解.题型一题型二题型三题型四题型五题型四题型五题型一题型二题型三易错辨析
易错点:忽视对项数的分类讨论而致误
【例5】 已知数列{an}满足 试求其前n项和.
错解:Sn=a1+a2+a3+…+an
=(a1+a3+a5+…+an-1)+(a2+a4+a6+…+an)错因分析:这里数列的通项an是关于n的分段函数,当n为奇数或为偶数时对应不同的法则,因此求和时必须对项数n进行分类讨论.题型四题型五题型一题型二题型三1 2 3 4 51已知数列{an}满足3an+1+an=0,a2=- ,则数列{an}的前10项和等于( )
A.-6(1-3-10) B. (1-310)
C.3(1-3-10) D.3(1+3-10)答案:C 1 2 3 4 5?1 2 3 4 53某人为了观看2018年世界杯,从2011年起,每年5月10日到银行存入a元定期储蓄,若年利率为p,且保持不变,并约定每年到期存款均自动转为新的一年定期,到2018年将所有的存款及利息全部取回,则可取回的总钱数为( )元.
A.a(1+p)7 B.a(1+p)8
解析:2011年存入的a元到2018年所得的本息和为a(1+p)7,2012年存入的a元到2018年所得的本息和为a(1+p)6,依此类推,则2017年存入的a元到2018年的本息和为a(1+p),每年所得的本息和构成一个以a(1+p)为首项,1+p为公比的等比数列,则到2018年取回的总额为a(1+p)+a(1+p)2+…+a(1+p)7=
答案:D4在等比数列{an}中,已知Sn=65,n=4,q= ,则a1= .? 1 2 3 4 5答案:27 1 2 3 4 55设数列{an}满足:a1=1,an+1=3an,n∈N+.
(1)求{an}的通项公式及前n项和Sn;
(2)已知{bn}是等差数列,Tn为其前n项和,且b1=a2,b3=a1+a2+a3,求T20.
