高中数学新人教B版必修5课件:第三章不等式3.1.1不等关系与不等式(27张)
文档属性
| 名称 | 高中数学新人教B版必修5课件:第三章不等式3.1.1不等关系与不等式(27张) |

|
|
| 格式 | zip | ||
| 文件大小 | 505.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-21 12:54:16 | ||
图片预览







文档简介
课件27张PPT。第三章 不等式3.1 不等关系与不等式3.1.1 不等关系与不等式1.了解不等式(组)的实际背景.
2.理解不等式的概念,了解实数运算的符号法则与两实数大小顺序之间的关系.
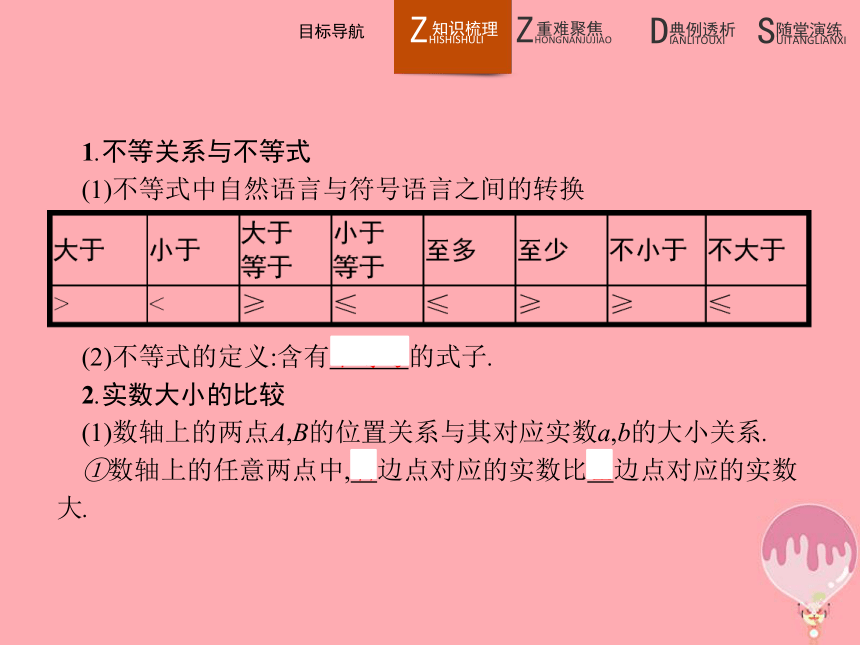
3.能用作差法比较大小.1.不等关系与不等式
(1)不等式中自然语言与符号语言之间的转换(2)不等式的定义:含有不等号的式子.
2.实数大小的比较
(1)数轴上的两点A,B的位置关系与其对应实数a,b的大小关系.
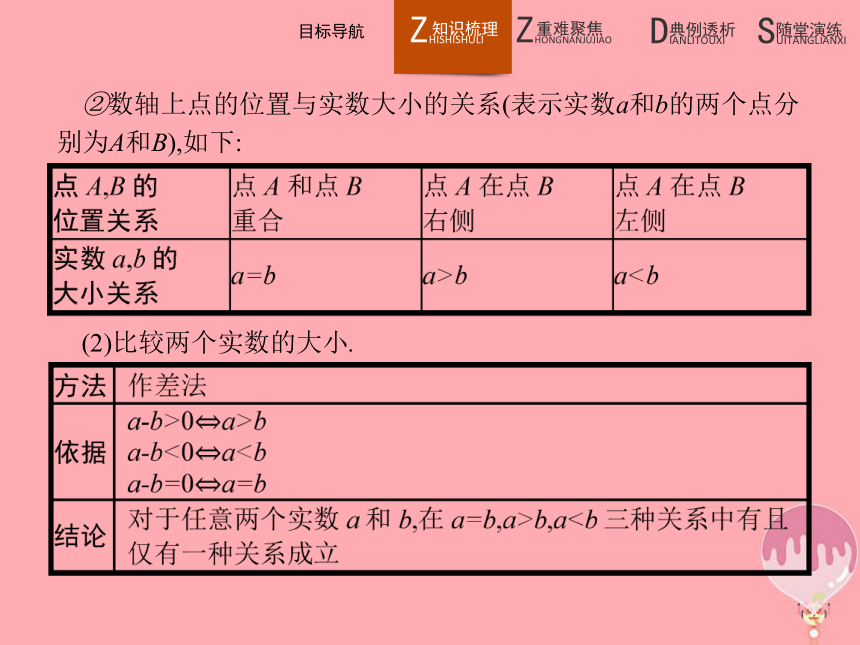
①数轴上的任意两点中,右边点对应的实数比左边点对应的实数大.②数轴上点的位置与实数大小的关系(表示实数a和b的两个点分别为A和B),如下:(2)比较两个实数的大小. 归纳总结作差法比较两个实数大小的基本步骤
(1)作差.
(2)变形.将两个实数作差,作差后变形为:
①常数;②几个平方和的形式;③几个因式积的形式.
(3)定号,即判断差的符号是正、负还是零.
(4)结论.利用实数大小之间的关系得出结论.【做一做1】 下面表示“a与b的差是非负数”的不等关系的是( )
A.a-b>0 B.a-b<0
C.a-b≥0 D.a-b≤0
答案:C
【做一做2】 设a,b>0, ,则P与Q的大小关系是( )
A.P≥Q B.P≤Q
C.P>Q D.P0,∴P2>Q2.∴P>Q.
答案:C一二一、比较大小常用的方法
剖析:证明一个不等式和比较实数的大小一样,根据题目的特点可以有不同的证明方法.
(1)作差法和作商法是比较实数大小和证明不等式的重要方法,但是它们又有各自的适用范围,在解决这些问题的时候,根据实际情况选择其中一种合适的方法.要根据题目的具体结构特点,和差的形式一般用作差法,乘除的形式一般用作商法.
①作差法要考虑作差后与0的比较,通常要进行因式分解,配方或者其他变形操作,所以,作差后必须变形到容易判断式子符号.一二②作商法主要适用于那些能够判断出恒为正数的数或者式子,具有一定的局限性,作商后要与1进行比较,所以,作商后必须易于变成能与1比较大小的式子,此种方法主要适用于那些含有幂指数的数或式子的大小比较,例如,比较aabb与 的大小就可以使用作商法.(2)要注意不等式与函数的结合,函数的图象和性质是解决不等式问题的重要工具,尤其是函数的单调性.如:a>b?a3>b3,可根据幂函数y=x3在R上单调递增得到.
名师点拨利用比较法来比较两个代数式或实数的大小时,注意分情况对变量进行讨论,讨论时应做到不重不漏.一二二、教材中的“思考与讨论” 题型一题型二题型三题型四用不等式(组)表示不等关系
【例1】 某矿山车队有4辆载重为10 t的甲型卡车和7辆载重为6 t的乙型卡车,有9名驾驶员.此车队每天至少要运360 t矿石至冶炼厂.已知甲型卡车每辆每天可往返6次,乙型卡车每辆每天可往返8次,写出满足上述所有不等关系的不等式.
分析:解答本题只需用不等式表示上述不等关系即可.
解:设每天派出甲型卡车x辆,乙型卡车y辆,则题型一题型二题型三题型四反思用不等式(组)表示实际问题中的不等关系时,应首先读懂题意,设出未知量,寻找不等关系的根源,将不等关系用未知量表示出来,即得到不等式或不等式组,这是应用不等式解决实际问题的最基本的一步.题型一题型二题型三题型四【变式训练1】 某厂使用两种零件A,B,装配甲、乙两种产品,该厂的生产能力是月产甲最多2 500件,月产乙最多1 200件,而组装一件甲需要4个A,2个B;组装一件乙需要6个A,8个B,某个月,该厂能用的A最多有14 000个,B最多有12 000个.用不等式将甲、乙两种产品产量之间的关系表示出来.
解:设甲、乙两种产品产量分别为x件、y件,
由题意,列不等式组如下:题型一题型二题型四题型三比较两数的大小
【例2】 当x≥1时,比较x3+1与2x2-2x+2的大小.
分析:根据a>b?a-b>0,a解:x3+1-(2x2-2x+2)=x3-2x2+2x-1
=x3-x2-(x2-2x+1)
=x2(x-1)-(x-1)2=(x-1)(x2-x+1)题型一题型二题型四题型三反思利用作差法比较大小时关键在于变形,变形的方向是将差式化成因式积的形式,然后确定每个因式的符号,从而确定积的符号.变形中常用到平方差、立方差、立方和等公式,还可能用到通分、因式分解、分子(或分母)有理化等方法.题型一题型二题型四题型三【变式训练2】 (1)若x(2)设a>0,b>0,且a≠b,试比较aabb与abba的大小.
解:(1)(x2+y2)(x-y)-(x2-y2)(x+y)=(x-y)[(x2+y2)-(x+y)2]=-2xy(x-y).
∵x0,x-y<0,∴-2xy(x-y)>0,
∴(x2+y2)(x-y)>(x2-y2)(x+y).题型一题型二题型三题型四不等关系的实际应用
【例3】 商店出售茶壶和茶杯,茶壶每个定价20元,茶杯每个定价5元,该店推出两种优惠办法:
(1)买一个茶壶赠送一个茶杯;
(2)按总价的92%付款.
某顾客需购茶壶4个,茶杯若干个(不少于4个),若设购买茶杯x个,付款y元,试分别建立两种优惠办法的y与x之间的函数关系式,并讨论该顾客买同样多的茶杯时,两种办法哪一种更省钱.
分析:本题是一次函数问题,通过建立两种优惠办法的一次函数模型,然后利用作差法讨论选哪种优惠办法.题型一题型二题型三题型四解:由优惠办法(1)得y1=20×4+5(x-4)=5x+60(x≥4),
由优惠办法(2)得y2=(5x+20×4)×92%=4.6x+73.6(x≥4).
y1-y2=0.4x-13.6(x≥4),
令y1-y2=0,得x=34.
当购买34个茶杯时,两种办法付款相同;当4≤x<34时,y134时,y1>y2,优惠办法(2)省钱.
反思利用作差法比较两个代数式的大小时,如果差式中有字母,就需要对字母的取值进行分类讨论.题型一题型二题型三题型四【变式训练3】 如果一辆汽车每天行驶的路程比原来多19 km,那么在8天内它的行程就超过2 200 km,如果它每天行驶的路程比原来少12 km,那么它行驶同样的路程得花9天多的时间,这辆汽车原来每天行驶路程(单位:km)的范围是多少?
解:设这辆汽车原来每天行驶的路程为x km,解得256所以这辆汽车原来每天行驶路程的范围是(256,260)(单位:km).题型一题型二题型三题型四易错辨析
易错点:忽视字母取值范围的讨论而致误错因分析:当n为偶数时,an-bn和an-1-bn-1不一定同号,这里忽略了在题设条件a+b>0且没有明确字母的具体值的情况下,要考虑分类讨论,即对a>0,b>0和a,b有一个负值的情况加以讨论.题型一题型二题型三题型四(2)当a,b有一个为负数时,不妨设a>0,b<0,且a+b>0,所以a>|b|.又n为偶数,所以(an-bn)·(an-1-bn-1)>0,且(ab)n>0,1 2 3 4 51下列不等式一定成立的是( )
A.-3<-4 B.0≤0
C.3≥4 D.-5≤-6
解析:不等式a≥b的含义是指“a>b,或者a=b”,不等式a≤b的含义是指“a答案:B1 2 3 4 52如果loga3>logb3,且a+b=1,那么( )
A.0C.1解析:∵a+b=1,a,b>0,
∴0b,则a3与b3的大小关系是 .? 所以a3>b3.
答案:a3>b31 2 3 4 54用“>”“<”“≥”或“≤”号填空.
(1)(2a+1)(a-3) (a-6)(2a+7)+45;?
(2)a2+b2 2(a-b-1).?
解析:(1)因为(2a+1)(a-3)-[(a-6)(2a+7)+45]=-6<0,所以(2a+1)(a-3)<(a-6)(2a+7)+45;
(2)因为a2+b2-2(a-b-1)=(a-1)2+(b+1)2≥0,
所以a2+b2≥2(a-b-1).
答案:(1)< (2)≥1 2 3 4 5
2.理解不等式的概念,了解实数运算的符号法则与两实数大小顺序之间的关系.
3.能用作差法比较大小.1.不等关系与不等式
(1)不等式中自然语言与符号语言之间的转换(2)不等式的定义:含有不等号的式子.
2.实数大小的比较
(1)数轴上的两点A,B的位置关系与其对应实数a,b的大小关系.
①数轴上的任意两点中,右边点对应的实数比左边点对应的实数大.②数轴上点的位置与实数大小的关系(表示实数a和b的两个点分别为A和B),如下:(2)比较两个实数的大小. 归纳总结作差法比较两个实数大小的基本步骤
(1)作差.
(2)变形.将两个实数作差,作差后变形为:
①常数;②几个平方和的形式;③几个因式积的形式.
(3)定号,即判断差的符号是正、负还是零.
(4)结论.利用实数大小之间的关系得出结论.【做一做1】 下面表示“a与b的差是非负数”的不等关系的是( )
A.a-b>0 B.a-b<0
C.a-b≥0 D.a-b≤0
答案:C
【做一做2】 设a,b>0, ,则P与Q的大小关系是( )
A.P≥Q B.P≤Q
C.P>Q D.P
答案:C一二一、比较大小常用的方法
剖析:证明一个不等式和比较实数的大小一样,根据题目的特点可以有不同的证明方法.
(1)作差法和作商法是比较实数大小和证明不等式的重要方法,但是它们又有各自的适用范围,在解决这些问题的时候,根据实际情况选择其中一种合适的方法.要根据题目的具体结构特点,和差的形式一般用作差法,乘除的形式一般用作商法.
①作差法要考虑作差后与0的比较,通常要进行因式分解,配方或者其他变形操作,所以,作差后必须变形到容易判断式子符号.一二②作商法主要适用于那些能够判断出恒为正数的数或者式子,具有一定的局限性,作商后要与1进行比较,所以,作商后必须易于变成能与1比较大小的式子,此种方法主要适用于那些含有幂指数的数或式子的大小比较,例如,比较aabb与 的大小就可以使用作商法.(2)要注意不等式与函数的结合,函数的图象和性质是解决不等式问题的重要工具,尤其是函数的单调性.如:a>b?a3>b3,可根据幂函数y=x3在R上单调递增得到.
名师点拨利用比较法来比较两个代数式或实数的大小时,注意分情况对变量进行讨论,讨论时应做到不重不漏.一二二、教材中的“思考与讨论” 题型一题型二题型三题型四用不等式(组)表示不等关系
【例1】 某矿山车队有4辆载重为10 t的甲型卡车和7辆载重为6 t的乙型卡车,有9名驾驶员.此车队每天至少要运360 t矿石至冶炼厂.已知甲型卡车每辆每天可往返6次,乙型卡车每辆每天可往返8次,写出满足上述所有不等关系的不等式.
分析:解答本题只需用不等式表示上述不等关系即可.
解:设每天派出甲型卡车x辆,乙型卡车y辆,则题型一题型二题型三题型四反思用不等式(组)表示实际问题中的不等关系时,应首先读懂题意,设出未知量,寻找不等关系的根源,将不等关系用未知量表示出来,即得到不等式或不等式组,这是应用不等式解决实际问题的最基本的一步.题型一题型二题型三题型四【变式训练1】 某厂使用两种零件A,B,装配甲、乙两种产品,该厂的生产能力是月产甲最多2 500件,月产乙最多1 200件,而组装一件甲需要4个A,2个B;组装一件乙需要6个A,8个B,某个月,该厂能用的A最多有14 000个,B最多有12 000个.用不等式将甲、乙两种产品产量之间的关系表示出来.
解:设甲、乙两种产品产量分别为x件、y件,
由题意,列不等式组如下:题型一题型二题型四题型三比较两数的大小
【例2】 当x≥1时,比较x3+1与2x2-2x+2的大小.
分析:根据a>b?a-b>0,a
=x3-x2-(x2-2x+1)
=x2(x-1)-(x-1)2=(x-1)(x2-x+1)题型一题型二题型四题型三反思利用作差法比较大小时关键在于变形,变形的方向是将差式化成因式积的形式,然后确定每个因式的符号,从而确定积的符号.变形中常用到平方差、立方差、立方和等公式,还可能用到通分、因式分解、分子(或分母)有理化等方法.题型一题型二题型四题型三【变式训练2】 (1)若x
解:(1)(x2+y2)(x-y)-(x2-y2)(x+y)=(x-y)[(x2+y2)-(x+y)2]=-2xy(x-y).
∵x
∴(x2+y2)(x-y)>(x2-y2)(x+y).题型一题型二题型三题型四不等关系的实际应用
【例3】 商店出售茶壶和茶杯,茶壶每个定价20元,茶杯每个定价5元,该店推出两种优惠办法:
(1)买一个茶壶赠送一个茶杯;
(2)按总价的92%付款.
某顾客需购茶壶4个,茶杯若干个(不少于4个),若设购买茶杯x个,付款y元,试分别建立两种优惠办法的y与x之间的函数关系式,并讨论该顾客买同样多的茶杯时,两种办法哪一种更省钱.
分析:本题是一次函数问题,通过建立两种优惠办法的一次函数模型,然后利用作差法讨论选哪种优惠办法.题型一题型二题型三题型四解:由优惠办法(1)得y1=20×4+5(x-4)=5x+60(x≥4),
由优惠办法(2)得y2=(5x+20×4)×92%=4.6x+73.6(x≥4).
y1-y2=0.4x-13.6(x≥4),
令y1-y2=0,得x=34.
当购买34个茶杯时,两种办法付款相同;当4≤x<34时,y1
反思利用作差法比较两个代数式的大小时,如果差式中有字母,就需要对字母的取值进行分类讨论.题型一题型二题型三题型四【变式训练3】 如果一辆汽车每天行驶的路程比原来多19 km,那么在8天内它的行程就超过2 200 km,如果它每天行驶的路程比原来少12 km,那么它行驶同样的路程得花9天多的时间,这辆汽车原来每天行驶路程(单位:km)的范围是多少?
解:设这辆汽车原来每天行驶的路程为x km,解得256
易错点:忽视字母取值范围的讨论而致误错因分析:当n为偶数时,an-bn和an-1-bn-1不一定同号,这里忽略了在题设条件a+b>0且没有明确字母的具体值的情况下,要考虑分类讨论,即对a>0,b>0和a,b有一个负值的情况加以讨论.题型一题型二题型三题型四(2)当a,b有一个为负数时,不妨设a>0,b<0,且a+b>0,所以a>|b|.又n为偶数,所以(an-bn)·(an-1-bn-1)>0,且(ab)n>0,1 2 3 4 51下列不等式一定成立的是( )
A.-3<-4 B.0≤0
C.3≥4 D.-5≤-6
解析:不等式a≥b的含义是指“a>b,或者a=b”,不等式a≤b的含义是指“a
A.0
∴0
答案:a3>b31 2 3 4 54用“>”“<”“≥”或“≤”号填空.
(1)(2a+1)(a-3) (a-6)(2a+7)+45;?
(2)a2+b2 2(a-b-1).?
解析:(1)因为(2a+1)(a-3)-[(a-6)(2a+7)+45]=-6<0,所以(2a+1)(a-3)<(a-6)(2a+7)+45;
(2)因为a2+b2-2(a-b-1)=(a-1)2+(b+1)2≥0,
所以a2+b2≥2(a-b-1).
答案:(1)< (2)≥1 2 3 4 5
