高中数学新人教B版必修5课件:第三章不等式3.5.2简单线性规划(41张)
文档属性
| 名称 | 高中数学新人教B版必修5课件:第三章不等式3.5.2简单线性规划(41张) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-21 00:00:00 | ||
图片预览










文档简介
课件41张PPT。3.5.2 简单线性规划1.体会线性规划的基本思想在求解实际问题中的作用,会求解简单的线性规划问题.
2.经历在线性约束条件下,求实际问题中的线性目标函数的最值问题的求解过程,提高用线性规划解决实际问题的能力.线性规划中的基本概念 名师点拨1.线性约束条件包括两点:一是关于变量x,y的不等式(或等式),二是次数为1.
2.目标函数与线性目标函数的概念不同,线性目标函数在变量x,y的次数上做了严格的限定:一次解析式,即目标函数包括线性目标函数和非线性目标函数.
3.可行解必须使线性约束条件成立,而可行域是所有的可行解构成的一个区域.【做一做1】 目标函数z=2x-y,将其看成直线方程时,z的意义是( )
A.该直线的截距 B.该直线的纵截距
C.该直线纵截距的相反数 D.该直线的横截距
解析:y=2x-z,故z的意义是该直线纵截距的相反数.故选C.
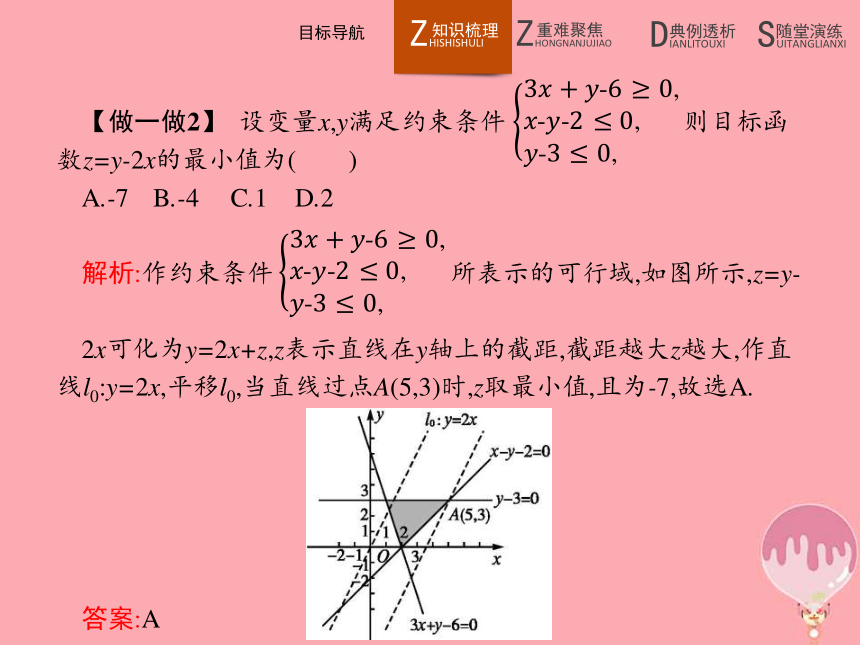
答案:C【做一做2】 设变量x,y满足约束条件 则目标函数z=y-2x的最小值为( )
A.-7 B.-4 C.1 D.2
解析:作约束条件 所表示的可行域,如图所示,z=y-
2x可化为y=2x+z,z表示直线在y轴上的截距,截距越大z越大,作直线l0:y=2x,平移l0,当直线过点A(5,3)时,z取最小值,且为-7,故选A.答案:A 一二一、图解法求最值的实质 且随z变化的一族平行线.于是,把求z的最大值和最小值的问题转化为直线与可行域有公共点时,直线在y轴上的截距的最大值和最小值的问题.当B>0时,z的值随着直线在y轴上的截距的增大而增大;当B<0时,z的值随着直线在y轴上的截距的增大而减小.
名师点拨1.如果可行域是一个多边形,那么一般在其顶点处可使目标函数取得最大或最小值,最优解一般就是多边形的某个顶点.
2.由于最优解是通过图形来观察的,故作图要准确,否则观察的结果可能有误.一二二、常见的线性规划问题类型
剖析:(1)线性规划的理论和方法主要在两类问题中得到应用:
一是在人力、物力、资金等资源一定的条件下,如何使用它们来完成最多的任务;
二是给定一项任务,如何合理安排和规划,能以最少的人力、物力、资金等资源来完成该项任务.
(2)线性规划问题的常见类型有:
①物资调运问题
例如已知A1,A2两煤矿每年的产量,煤需经B1,B2两个车站运往外地,B1,B2两车站的运输能力是有限的,且已知A1,A2两煤矿运往B1,B2两车站的运输价格,煤矿应怎样编制调运方案,能使总运费最少?一二②产品安排问题
例如某工厂生产甲、乙两种产品,每生产一个单位的甲种或乙种产品所需A,B,C三种材料的数量、此厂每月所能提供的三种材料的限额、每生产一个单位甲种或乙种产品所获利润额都是已知的,这个厂每月应如何安排产品的生产,才能使每月获得的总利润最大?
③下料问题
例如要把一批长钢管截成两种规格的短钢管,怎样下料能使损耗最小?题型一题型二题型三题型四题型五题型六线性目标函数的最值问题
【例1】 若变量x,y满足约束条件 且z=5y-x的最大
值为a,最小值为b,则a-b的值是( )
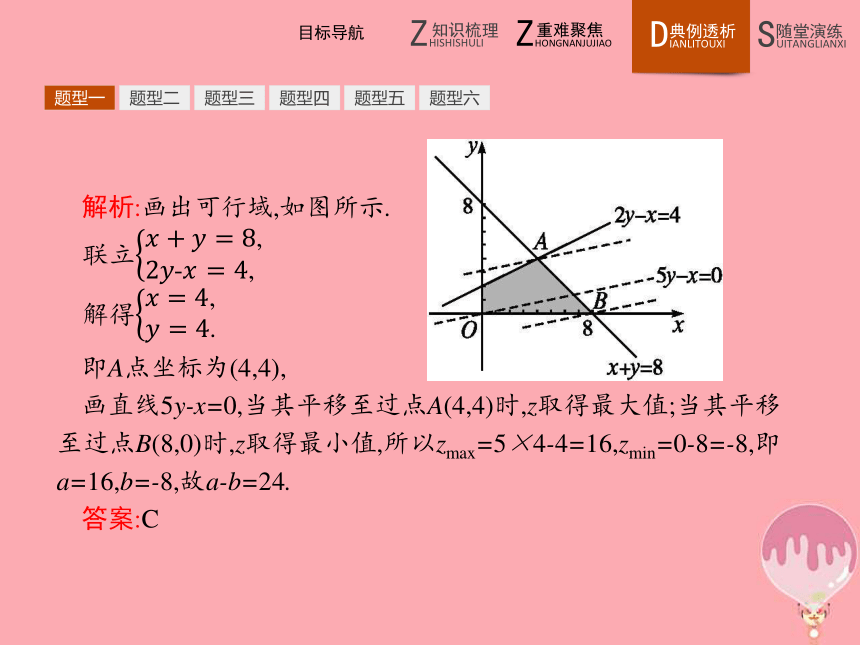
A.48 B.30 C.24 D.16题型一题型二题型三题型四题型五题型六解析:画出可行域,如图所示. 即A点坐标为(4,4),
画直线5y-x=0,当其平移至过点A(4,4)时,z取得最大值;当其平移至过点B(8,0)时,z取得最小值,所以zmax=5×4-4=16,zmin=0-8=-8,即a=16,b=-8,故a-b=24.
答案:C题型一题型二题型三题型四题型五题型六反思在确定线性约束条件和线性目标函数的前提下,用图解法求最优解的步骤概括为“画、移、求、答”,即:
(1)画:在直角坐标平面上画出可行域和直线ax+by=0(目标函数为z=ax+by);
(2)移:平行移动直线ax+by=0,确定使z=ax+by取得最大值或最小值的点;
(3)求:求出取得最大值或最小值的点的坐标(解方程组)及最大值和最小值;
(4)答:给出正确答案.题型一题型二题型三题型四题型五题型六【变式训练1】 设变量x,y满足约束条件
则目标函数z=3x-2y的最小值为( )
A.-5 B.-4
C.-2 D.3
解析:画出可行域,如图所示的阴影部分,作直线l0:3x-2y=0,平移至点A时,目标函数取得最小值,且A(0,2),故zmin=3×0-2×2=-4.答案:B 题型一题型二题型四题型五题型三题型六【例2】 若实数x,y满足不等式组 且x+y的最大值为9,则实数m=( )
A.-2 B.-1 C.1 D.2
解析:作出可行域,如图中阴影部分所示.题型一题型二题型四题型五题型三题型六解得m=1.
答案:C
反思已知目标函数的最值,求线性约束条件的参数问题,可以先画出线性约束条件中的已知部分,由于最值一般在可行域的顶点或边界处取得,常常利用数形结合的方法求解.题型一题型二题型四题型五题型三题型六【变式训练2】 已知x,y满足 设z=ax+y(a>0),若
当z取最大值时对应的点有无数多个,求a的值.解:由约束条件画出可行域,如图中阴影部分所示.
一般情况下,当z取最大值时,直线所经过的点都是唯一的,但若直线平行于边界直线,如图所示,即直线z=ax+y(a>0)平行于直线AC,则直线经过线段AC上任意一点时,z均取得最大值,此时满足条件,即有无数多个点使函数取得最大值.题型一题型二题型四题型五题型三题型六分析知,当直线y=-ax+z刚好移动到直线AC时,将会有无数多个点使函数取得最大值.题型一题型二题型三题型四题型五题型六非线性目标函数的最值问题 题型一题型二题型三题型四题型五题型六解:作出可行域,如图阴影部分所示.可求得A(1,3),B(3,1),C(7,9). 题型一题型二题型三题型四题型五题型六题型一题型二题型三题型四题型五题型六题型一题型二题型三题型四题型五题型六解:(1)u=x2+y2表示可行域内的点到原点O的距离的平方,由图可知,点C(3,8)到原点O的距离最大,点O(0 ,0)到原点O的距离最小,
所以umax=73,umin=0.题型一题型二题型三题型四题型五题型六题型一题型二题型三题型四题型五题型六简单的线性规划问题
【例4】 某校伙食长期以面粉和大米为主食,面食每100克含蛋白质6个单位,含淀粉4个单位,售价0.5元,米饭每100克含蛋白质3个单位,含淀粉7个单位,售价0.4元,学校要求给学生配制盒饭,每盒盒饭至少有8个单位的蛋白质和10个单位的淀粉,问应如何配制盒饭,才既科学又费用最少?
分析:根据实际问题中的已知条件,找出约束条件和目标函数,再用图解法解之.先作可行域,再作出初始直线l0,通过向上或向下平移直线l0至可行域的边界点,便得最优解,再进一步求最值.题型一题型二题型三题型四题型五题型六解:设每盒盒饭需要面食x百克,米饭y百克, 作出可行域,如图阴影部分所示. 令z=0,作直线l0:0.5x+0.4y=0,即直线5x+4y=0.
由图形可知,把直线l0平移至过点A时,z取最小值.题型一题型二题型三题型四题型五题型六反思1.在线性规划应用问题中,常常是题中的条件较多,因此认真审题非常重要.
2.线性约束条件中有无等号要依据条件加以判断.
3.结合实际问题,分析未知数x,y等是否有限制,如x,y为正整数、非负数等.
4.分清线性约束条件和线性目标函数,线性约束条件一般是不等式,而线性目标函数却是一个等式.
5.图对解决线性规划问题至关重要,关键步骤基本上都是在图上完成的,所以作图应尽可能准确,图上操作尽可能规范.但作图中必然会有误差,假如图上的最优点不容易看出时,需将几个有可能是最优点的坐标都求出来,然后逐一检查,以确定最优解.题型一题型二题型三题型四题型五题型六【变式训练4】 某工厂投资生产A产品时,每生产一百吨需要资金200万元,需场地200平方米,可获得利润300万元;投资生产B产品时,每生产一百吨需要资金300万元,需场地100平方米,可获利润200万元.现某单位可使用资金1 400万元,场地900平方米,问应做怎样的组合投资,可使获利最大?
分析:这是一个线性规划问题,可将题中数据整理成下表,设未知数列出约束条件和目标函数,最后作图求解.题型一题型二题型三题型四题型五题型六解:设生产A产品x百吨,生产B产品y百吨,利润为S百万元, 作出可行域(如图阴影部分所示), 题型一题型二题型三题型四题型五题型六与可行域相交.由图知,使3x+2y取得最大值的(x,y)是两直线2x+y=9与2x+3y=14的交点M(3.25,2.50).此时Smax=3×3.25+2×2.50=14.75.
答:生产A产品3.25百吨,生产B产品2.50百吨时,获利最大,且最大利润为14.75百万元.题型四题型五题型一题型二题型三题型六最优整数解的问题
【例5】 某旅行社租用A,B两种型号的客车安排900名客人旅行,A,B两种车辆的载客量分别为36人和60人,租金分别为1 600元/辆和2 400元/辆,旅行社要求租车总数不超过21辆,且B型车不多于A型车7辆,则租金最少为( )
A.31 200元 B.36 000元
C.36 800元 D.38 400元
解析:设需A,B型车分别为x,y辆(x,y∈N),题型四题型五题型一题型二题型三题型六设租金为z,则z=1 600x+2 400y,画出可行域如图,根据线性规划中截距问题,可求得最优解为x=5,y=12,此时z最小等于36 800,故选C.答案:C
反思如果要求最优整数解,可先求出线性规划的最优解,若它是整数解,则问题解决;若不是,要在该非整数解周围可行域内寻求与之最近的整数解,可通过精确作图,打网格的办法求得.题型四题型五题型一题型二题型三题型六【变式训练5】 配制A,B两种药剂,需要甲、乙两种原料,已知配一剂A种药需甲料3毫克,乙料5毫克;配一剂B种药需甲料5毫克,乙料4毫克,今有甲料20毫克,乙料25毫克,若A,B两种药至少各配一剂,问共有多少种配制方法?若A种药价值10元,B种药价值20元,则配出的药价值最大为多少?上述不等式组的解集是以直线x=1,y=1,3x+5y=20及5x+4y=25为边界所围成的区域内的整点(如图所示),这个区域内的整点为(1,1),(1,2),(1,3),(2,1),(2,2),(3,1),(3,2),(4,1).题型四题型五题型一题型二题型三题型六所以,在至少各配一剂的情况下,共有8种不同的配制方法.
由目标函数z=10x+20y,作直线l:10x+20y=0,平移直线l过整点(1,3)和(3,2)时,z最大,此时zmax=70(元).题型四题型五题型一题型二题型三题型六易错辨析
易错点:在解答线性规划实际问题时,因忽视整点的要求而致误
【例6】 某公司招收男职员x名,女职员y名,x和y需满足约束条件
则z=10x+10y的最大值是 .?题型四题型五题型一题型二题型三题型六答案:90 1 2 3 4 51若变量x,y满足约束条件 则z=2x+y的最大值和最小值分别为( )
A.4和3 B.4和2
C.3和2 D.2和0
解析:画出可行域如图阴影部分所示.
画出直线2x+y=0,并向可行域方向移动,
当直线经过点(1,0)时,z取最小值.
当直线经过点(2,0)时,z取最大值.
故zmax=2×2+0=4,zmin=2×1+0=2.
答案:B1 2 3 4 52设E为平面上以三点A(4,1),B(-1,-6),C(-3,2)为顶点的三角形区域(包括边界),则z=4x-3y,(x,y)∈E的最大值与最小值分别为( )
A.14,-18 B.-14,-18
C.18,14 D.18,-14
解析:当动直线z=4x-3y通过点B时,z取最大值,通过点C时,z取最小值,即zmax=4×(-1)-3×(-6)=14,zmin=4×(-3)-3×2=-18.
答案:A1 2 3 4 53已知变量x,y满足 则z=3x+y的最大值是 .?
答案:161 2 3 4 54已知变量x,y满足约束条件1≤x+y≤4,-2≤x-y≤2.若目标函数z=ax+y(其中a>0)仅在点(3,1)处取得最大值,则a的取值范围为 .?
解析:变量x,y满足约束条件1≤x+y≤4,-2≤x-y≤2.在直角坐标系中画出可行域,如图阴影部分所示,得四边形ABCD,其中A(3,1),kAD=1,kAB=-1,目标函数z=ax+y(其中a>0)中的z表示斜率为-a的直线截距的大小,若仅在点(3,1)处取得最大值,则斜率应小于kAB=-1,即-a<-1,即a>1,所以a的取值范围为(1,+∞).答案:(1,+∞) 1 2 3 4 55某营养师要为某个儿童预订午餐和晚餐,已知1个单位的午餐含12个单位的碳水化合物,6个单位的蛋白质和6个单位的维生素C;1个单位的晚餐含8个单位的碳水化合物,6个单位的蛋白质和10个单位的维生素C.另外,该儿童这两餐需要的营养中至少含64个单位的碳水化合物,42个单位的蛋白质和54个单位的维生素C.
如果1个单位的午餐、晚餐的费用分别是2.5元和4元,那么要满足上述的营养要求,并且花费最少,应当为该儿童分别预订多少个单位的午餐和晚餐?
解:设需要预订满足要求的午餐和晚餐分别为x个单位和y个单位,所花的费用为z元,则依题意,得z=2.5x+4y,且x,y满足1 2 3 4 5作出可行域如图阴影部分所示,画出直线2.5x+4y=0,使其在可行域上平移,由此可知z=2.5x+4y在B(4,3)处取得最小值.
因此,应当为该儿童预订4个单位的午餐和3个单位的晚餐,就可满足要求.
2.经历在线性约束条件下,求实际问题中的线性目标函数的最值问题的求解过程,提高用线性规划解决实际问题的能力.线性规划中的基本概念 名师点拨1.线性约束条件包括两点:一是关于变量x,y的不等式(或等式),二是次数为1.
2.目标函数与线性目标函数的概念不同,线性目标函数在变量x,y的次数上做了严格的限定:一次解析式,即目标函数包括线性目标函数和非线性目标函数.
3.可行解必须使线性约束条件成立,而可行域是所有的可行解构成的一个区域.【做一做1】 目标函数z=2x-y,将其看成直线方程时,z的意义是( )
A.该直线的截距 B.该直线的纵截距
C.该直线纵截距的相反数 D.该直线的横截距
解析:y=2x-z,故z的意义是该直线纵截距的相反数.故选C.
答案:C【做一做2】 设变量x,y满足约束条件 则目标函数z=y-2x的最小值为( )
A.-7 B.-4 C.1 D.2
解析:作约束条件 所表示的可行域,如图所示,z=y-
2x可化为y=2x+z,z表示直线在y轴上的截距,截距越大z越大,作直线l0:y=2x,平移l0,当直线过点A(5,3)时,z取最小值,且为-7,故选A.答案:A 一二一、图解法求最值的实质 且随z变化的一族平行线.于是,把求z的最大值和最小值的问题转化为直线与可行域有公共点时,直线在y轴上的截距的最大值和最小值的问题.当B>0时,z的值随着直线在y轴上的截距的增大而增大;当B<0时,z的值随着直线在y轴上的截距的增大而减小.
名师点拨1.如果可行域是一个多边形,那么一般在其顶点处可使目标函数取得最大或最小值,最优解一般就是多边形的某个顶点.
2.由于最优解是通过图形来观察的,故作图要准确,否则观察的结果可能有误.一二二、常见的线性规划问题类型
剖析:(1)线性规划的理论和方法主要在两类问题中得到应用:
一是在人力、物力、资金等资源一定的条件下,如何使用它们来完成最多的任务;
二是给定一项任务,如何合理安排和规划,能以最少的人力、物力、资金等资源来完成该项任务.
(2)线性规划问题的常见类型有:
①物资调运问题
例如已知A1,A2两煤矿每年的产量,煤需经B1,B2两个车站运往外地,B1,B2两车站的运输能力是有限的,且已知A1,A2两煤矿运往B1,B2两车站的运输价格,煤矿应怎样编制调运方案,能使总运费最少?一二②产品安排问题
例如某工厂生产甲、乙两种产品,每生产一个单位的甲种或乙种产品所需A,B,C三种材料的数量、此厂每月所能提供的三种材料的限额、每生产一个单位甲种或乙种产品所获利润额都是已知的,这个厂每月应如何安排产品的生产,才能使每月获得的总利润最大?
③下料问题
例如要把一批长钢管截成两种规格的短钢管,怎样下料能使损耗最小?题型一题型二题型三题型四题型五题型六线性目标函数的最值问题
【例1】 若变量x,y满足约束条件 且z=5y-x的最大
值为a,最小值为b,则a-b的值是( )
A.48 B.30 C.24 D.16题型一题型二题型三题型四题型五题型六解析:画出可行域,如图所示. 即A点坐标为(4,4),
画直线5y-x=0,当其平移至过点A(4,4)时,z取得最大值;当其平移至过点B(8,0)时,z取得最小值,所以zmax=5×4-4=16,zmin=0-8=-8,即a=16,b=-8,故a-b=24.
答案:C题型一题型二题型三题型四题型五题型六反思在确定线性约束条件和线性目标函数的前提下,用图解法求最优解的步骤概括为“画、移、求、答”,即:
(1)画:在直角坐标平面上画出可行域和直线ax+by=0(目标函数为z=ax+by);
(2)移:平行移动直线ax+by=0,确定使z=ax+by取得最大值或最小值的点;
(3)求:求出取得最大值或最小值的点的坐标(解方程组)及最大值和最小值;
(4)答:给出正确答案.题型一题型二题型三题型四题型五题型六【变式训练1】 设变量x,y满足约束条件
则目标函数z=3x-2y的最小值为( )
A.-5 B.-4
C.-2 D.3
解析:画出可行域,如图所示的阴影部分,作直线l0:3x-2y=0,平移至点A时,目标函数取得最小值,且A(0,2),故zmin=3×0-2×2=-4.答案:B 题型一题型二题型四题型五题型三题型六【例2】 若实数x,y满足不等式组 且x+y的最大值为9,则实数m=( )
A.-2 B.-1 C.1 D.2
解析:作出可行域,如图中阴影部分所示.题型一题型二题型四题型五题型三题型六解得m=1.
答案:C
反思已知目标函数的最值,求线性约束条件的参数问题,可以先画出线性约束条件中的已知部分,由于最值一般在可行域的顶点或边界处取得,常常利用数形结合的方法求解.题型一题型二题型四题型五题型三题型六【变式训练2】 已知x,y满足 设z=ax+y(a>0),若
当z取最大值时对应的点有无数多个,求a的值.解:由约束条件画出可行域,如图中阴影部分所示.
一般情况下,当z取最大值时,直线所经过的点都是唯一的,但若直线平行于边界直线,如图所示,即直线z=ax+y(a>0)平行于直线AC,则直线经过线段AC上任意一点时,z均取得最大值,此时满足条件,即有无数多个点使函数取得最大值.题型一题型二题型四题型五题型三题型六分析知,当直线y=-ax+z刚好移动到直线AC时,将会有无数多个点使函数取得最大值.题型一题型二题型三题型四题型五题型六非线性目标函数的最值问题 题型一题型二题型三题型四题型五题型六解:作出可行域,如图阴影部分所示.可求得A(1,3),B(3,1),C(7,9). 题型一题型二题型三题型四题型五题型六题型一题型二题型三题型四题型五题型六题型一题型二题型三题型四题型五题型六解:(1)u=x2+y2表示可行域内的点到原点O的距离的平方,由图可知,点C(3,8)到原点O的距离最大,点O(0 ,0)到原点O的距离最小,
所以umax=73,umin=0.题型一题型二题型三题型四题型五题型六题型一题型二题型三题型四题型五题型六简单的线性规划问题
【例4】 某校伙食长期以面粉和大米为主食,面食每100克含蛋白质6个单位,含淀粉4个单位,售价0.5元,米饭每100克含蛋白质3个单位,含淀粉7个单位,售价0.4元,学校要求给学生配制盒饭,每盒盒饭至少有8个单位的蛋白质和10个单位的淀粉,问应如何配制盒饭,才既科学又费用最少?
分析:根据实际问题中的已知条件,找出约束条件和目标函数,再用图解法解之.先作可行域,再作出初始直线l0,通过向上或向下平移直线l0至可行域的边界点,便得最优解,再进一步求最值.题型一题型二题型三题型四题型五题型六解:设每盒盒饭需要面食x百克,米饭y百克, 作出可行域,如图阴影部分所示. 令z=0,作直线l0:0.5x+0.4y=0,即直线5x+4y=0.
由图形可知,把直线l0平移至过点A时,z取最小值.题型一题型二题型三题型四题型五题型六反思1.在线性规划应用问题中,常常是题中的条件较多,因此认真审题非常重要.
2.线性约束条件中有无等号要依据条件加以判断.
3.结合实际问题,分析未知数x,y等是否有限制,如x,y为正整数、非负数等.
4.分清线性约束条件和线性目标函数,线性约束条件一般是不等式,而线性目标函数却是一个等式.
5.图对解决线性规划问题至关重要,关键步骤基本上都是在图上完成的,所以作图应尽可能准确,图上操作尽可能规范.但作图中必然会有误差,假如图上的最优点不容易看出时,需将几个有可能是最优点的坐标都求出来,然后逐一检查,以确定最优解.题型一题型二题型三题型四题型五题型六【变式训练4】 某工厂投资生产A产品时,每生产一百吨需要资金200万元,需场地200平方米,可获得利润300万元;投资生产B产品时,每生产一百吨需要资金300万元,需场地100平方米,可获利润200万元.现某单位可使用资金1 400万元,场地900平方米,问应做怎样的组合投资,可使获利最大?
分析:这是一个线性规划问题,可将题中数据整理成下表,设未知数列出约束条件和目标函数,最后作图求解.题型一题型二题型三题型四题型五题型六解:设生产A产品x百吨,生产B产品y百吨,利润为S百万元, 作出可行域(如图阴影部分所示), 题型一题型二题型三题型四题型五题型六与可行域相交.由图知,使3x+2y取得最大值的(x,y)是两直线2x+y=9与2x+3y=14的交点M(3.25,2.50).此时Smax=3×3.25+2×2.50=14.75.
答:生产A产品3.25百吨,生产B产品2.50百吨时,获利最大,且最大利润为14.75百万元.题型四题型五题型一题型二题型三题型六最优整数解的问题
【例5】 某旅行社租用A,B两种型号的客车安排900名客人旅行,A,B两种车辆的载客量分别为36人和60人,租金分别为1 600元/辆和2 400元/辆,旅行社要求租车总数不超过21辆,且B型车不多于A型车7辆,则租金最少为( )
A.31 200元 B.36 000元
C.36 800元 D.38 400元
解析:设需A,B型车分别为x,y辆(x,y∈N),题型四题型五题型一题型二题型三题型六设租金为z,则z=1 600x+2 400y,画出可行域如图,根据线性规划中截距问题,可求得最优解为x=5,y=12,此时z最小等于36 800,故选C.答案:C
反思如果要求最优整数解,可先求出线性规划的最优解,若它是整数解,则问题解决;若不是,要在该非整数解周围可行域内寻求与之最近的整数解,可通过精确作图,打网格的办法求得.题型四题型五题型一题型二题型三题型六【变式训练5】 配制A,B两种药剂,需要甲、乙两种原料,已知配一剂A种药需甲料3毫克,乙料5毫克;配一剂B种药需甲料5毫克,乙料4毫克,今有甲料20毫克,乙料25毫克,若A,B两种药至少各配一剂,问共有多少种配制方法?若A种药价值10元,B种药价值20元,则配出的药价值最大为多少?上述不等式组的解集是以直线x=1,y=1,3x+5y=20及5x+4y=25为边界所围成的区域内的整点(如图所示),这个区域内的整点为(1,1),(1,2),(1,3),(2,1),(2,2),(3,1),(3,2),(4,1).题型四题型五题型一题型二题型三题型六所以,在至少各配一剂的情况下,共有8种不同的配制方法.
由目标函数z=10x+20y,作直线l:10x+20y=0,平移直线l过整点(1,3)和(3,2)时,z最大,此时zmax=70(元).题型四题型五题型一题型二题型三题型六易错辨析
易错点:在解答线性规划实际问题时,因忽视整点的要求而致误
【例6】 某公司招收男职员x名,女职员y名,x和y需满足约束条件
则z=10x+10y的最大值是 .?题型四题型五题型一题型二题型三题型六答案:90 1 2 3 4 51若变量x,y满足约束条件 则z=2x+y的最大值和最小值分别为( )
A.4和3 B.4和2
C.3和2 D.2和0
解析:画出可行域如图阴影部分所示.
画出直线2x+y=0,并向可行域方向移动,
当直线经过点(1,0)时,z取最小值.
当直线经过点(2,0)时,z取最大值.
故zmax=2×2+0=4,zmin=2×1+0=2.
答案:B1 2 3 4 52设E为平面上以三点A(4,1),B(-1,-6),C(-3,2)为顶点的三角形区域(包括边界),则z=4x-3y,(x,y)∈E的最大值与最小值分别为( )
A.14,-18 B.-14,-18
C.18,14 D.18,-14
解析:当动直线z=4x-3y通过点B时,z取最大值,通过点C时,z取最小值,即zmax=4×(-1)-3×(-6)=14,zmin=4×(-3)-3×2=-18.
答案:A1 2 3 4 53已知变量x,y满足 则z=3x+y的最大值是 .?
答案:161 2 3 4 54已知变量x,y满足约束条件1≤x+y≤4,-2≤x-y≤2.若目标函数z=ax+y(其中a>0)仅在点(3,1)处取得最大值,则a的取值范围为 .?
解析:变量x,y满足约束条件1≤x+y≤4,-2≤x-y≤2.在直角坐标系中画出可行域,如图阴影部分所示,得四边形ABCD,其中A(3,1),kAD=1,kAB=-1,目标函数z=ax+y(其中a>0)中的z表示斜率为-a的直线截距的大小,若仅在点(3,1)处取得最大值,则斜率应小于kAB=-1,即-a<-1,即a>1,所以a的取值范围为(1,+∞).答案:(1,+∞) 1 2 3 4 55某营养师要为某个儿童预订午餐和晚餐,已知1个单位的午餐含12个单位的碳水化合物,6个单位的蛋白质和6个单位的维生素C;1个单位的晚餐含8个单位的碳水化合物,6个单位的蛋白质和10个单位的维生素C.另外,该儿童这两餐需要的营养中至少含64个单位的碳水化合物,42个单位的蛋白质和54个单位的维生素C.
如果1个单位的午餐、晚餐的费用分别是2.5元和4元,那么要满足上述的营养要求,并且花费最少,应当为该儿童分别预订多少个单位的午餐和晚餐?
解:设需要预订满足要求的午餐和晚餐分别为x个单位和y个单位,所花的费用为z元,则依题意,得z=2.5x+4y,且x,y满足1 2 3 4 5作出可行域如图阴影部分所示,画出直线2.5x+4y=0,使其在可行域上平移,由此可知z=2.5x+4y在B(4,3)处取得最小值.
因此,应当为该儿童预订4个单位的午餐和3个单位的晚餐,就可满足要求.
