高中数学新人教B版必修5课件:第三章不等式本章整合(44张)
文档属性
| 名称 | 高中数学新人教B版必修5课件:第三章不等式本章整合(44张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-21 00:00:00 | ||
图片预览











文档简介
课件44张PPT。本章整合专题一专题二专题三专题四专题五专题六专题一 用函数的图象解不等式
函数是中学数学中的重点内容之一,它贯穿于中学数学教学的始终,而利用函数的图象能直观、准确、迅速地分析研究函数的性质或解决与函数有关的问题,因此,函数图象是高考考查的重点内容,在历年高考中都有涉及.
函数图象形象地显示了函数的性质,为研究数量关系提供了形的直观性,它是探求解题路径、获得问题结果的重要工具,在解方程或不等式时,特别是非常规的方程或不等式,有时需要画出图象,利用数形结合能起到十分快捷的效果.专题一专题二专题三专题四专题五专题六应用1已知函数f(x)= 若方程f(x)=k无实根,则实数
k的取值范围是( )提示:所给的函数f(x)是分段函数,而方程f(x)=k无实数根,可利用数形结合法转化为函数图象无交点.专题一专题二专题三专题四专题五专题六解析:在同一坐标系内作出y=f(x)与y=k的图象,如图所示, 答案:C 专题一专题二专题三专题四专题五专题六应用2已知a,b,c依次是方程2x+x=0,log2x=2-x和 =x的实数根,则a,b,c的大小关系是 .?
提示:构造常见的初等函数,利用函数的图象可解决问题.
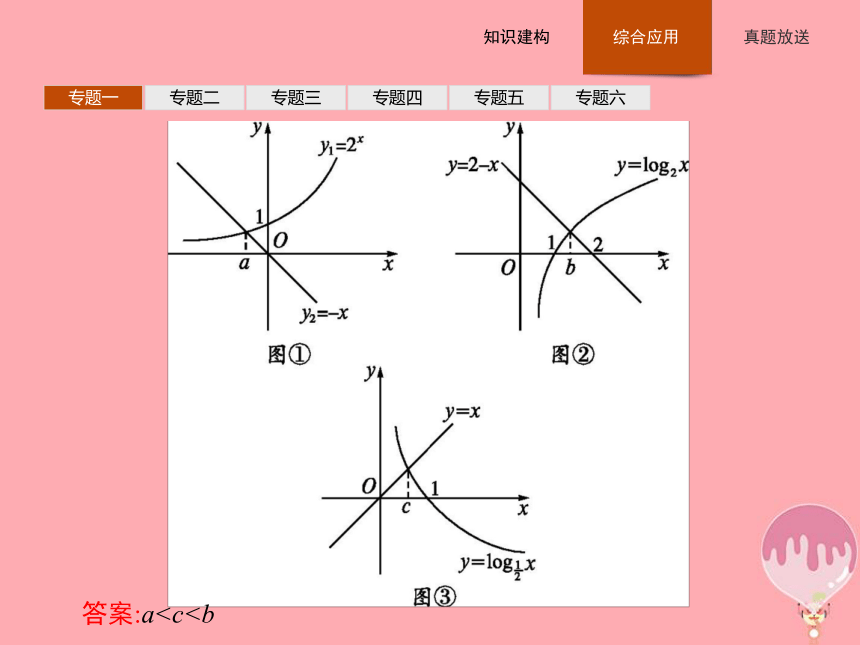
解析:由2x+x=0,得2x=-x,设函数y1=2x,y2=-x,分别作出它们的图象,如图①,两图象交点的横坐标为a,可得a<0,同理,对于方程log2x=2-x,可得图②,得1常见的不等式有一元一次不等式,一元二次不等式,简单的高次不等式,分式不等式,含有指数、对数的不等式,其解法为:
(1)解一元二次不等式,画出其对应的二次函数图象,来确定解集.
(2)解高次不等式常用穿根法.
(3)分式不等式利用不等式的性质将其转化为整式不等式(组)求解.
(4)解含有指数、对数的不等式时,利用指数与对数函数的单调性,将指数、对数不等式转化成与之等价的不等式(组)求解.专题一专题二专题三专题四专题五专题六应用1求解下列不等式:
(1)-x2+2x+3<0;
(2)x3+2x2-3x>0;提示:(1)注意解一元二次不等式的几个步骤.
(2)穿根法求解.
(3)转化为整式不等式,注意分母不为0.
(4)对数不等式,真数大于0.
解:(1)因为-x2+2x+3<0,所以x2-2x-3>0.
又方程x2-2x-3=0的两根为x1=-1,x2=3,
所以原不等式的解集为{x|x>3或x<-1}.专题一专题二专题三专题四专题五专题六(2)由x3+2x2-3x=x(x2+2x-3)=x(x+3)(x-1),可令f(x)=x(x-1)(x+3),
因为f(x)=0的根为-3,0,1,
所以由穿根法(如图),得不等式x3+2x2-3x>0的解集为{x|x>1或-3即(x-1)(x+2)(x-2)≥0,且x≠2,
如图,由穿根法得原不等式的解集为{x|-2≤x≤1或x>2}.专题一专题二专题三专题四专题五专题六专题一专题二专题三专题四专题五专题六应用2解关于x的不等式(x-2)(ax-2)>0.
提示:二次项系数为a,需对a的正负进行讨论;还要对根的大小进行讨论,两者要同时进行.
解:(1)当a=0时,原不等式化为(x-2)·(-2)>0,即x-2<0,所以x<2.专题一专题二专题三专题四专题五专题六综上所述,不等式的解集为
当a=0时,{x|x<2};
当a=1时,{x|x≠2};专题一专题二专题三专题四专题五专题六专题三 利用均值不等式求最值的常用方法
均值不等式是一个重要的不等式,利用它可以求解某些函数最值问题.对于有些题目,可以直接利用均值不等式求解.但是有些题目必须进行必要的变形才能利用均值不等式求解.常见的变形方法为配凑法、整体代换法等.下面介绍一些常用的变形方法.
1.凑系数
应用1已知0提示:由00,利用均值不等式求最值,必须和为定值或积为定值,此题为两个式子积的形式,但其和不是定值.注意到2x+(10-2x)=10为定值,故只需将y=x(10-2x)凑上一个系数即可.专题一专题二专题三专题四专题五专题六2.凑项法 提示:由题意知4x-5<0,首先要调整符号,又(4x-2)· 不是定值,故需对4x-2进行凑项才能得到定值.专题一专题二专题三专题四专题五专题六3.分离法 提示:本题看似无法运用均值不等式,不妨将分子配方凑出含有(x+1)的项,再将其分离.专题一专题二专题三专题四专题五专题六4.整体代换法 当且仅当x=12,y=24时,等号成立,
所以x+y的最小值为36.专题一专题二专题三专题四专题五专题六专题四 不等式恒成立问题
恒成立问题,涉及一次函数、二次函数的性质、图象,渗透着换元、化归、数形结合、函数与方程等思想方法,是很综合的一个题型,也是历年高考的一个热点.变量分离法和数形结合的方法比较常用,数形结合的方法较简单.当然还有其他的解决方法,如赋值法、根据对称性等.专题一专题二专题三专题四专题五专题六1.一次函数型
应用1对于满足|p|≤2的所有实数p,求使关于x的不等式x2+px+1>p+2x恒成立的x的取值范围.
提示:在不等式中出现了两个字母:x和p,关键在于该把哪个字母看成是变量.本题可将p视作变量,则上述问题即可转化为在[-2,2]内关于p的一次函数大于0恒成立的问题.
解:原不等式即(x-1)p+x2-2x+1>0,设f(p)=(x-1)p+x2-2x+1,则f(p)在[-2,2]上恒大于0,故有:专题一专题二专题三专题四专题五专题六2.二次函数型
应用2设f(x)=x2-2ax+2,当x∈[-1,+∞)时,都有f(x)≥a恒成立,求a的取值范围.
提示:题目中要证明f(x)≥a恒成立,若把a移到等号的左边,则把原题转化成左边二次函数在区间[-1,+∞)内恒大于0的问题,就可以利用函数的图象解决了.
解:设F(x)=f(x)-a=x2-2ax+2-a.
(1)当Δ=4a2-4(2-a)=4(a-1)(a+2) ≤0,即-2≤a≤1时,对一切x∈[-1,+∞),F(x)≥0恒成立;专题一专题二专题三专题四专题五专题六(2)当Δ=4(a-1)(a+2) >0时,由图可得以下充要条件:
得-3≤a<-2.
综上可得a的取值范围为[-3,1].专题一专题二专题三专题四专题五专题六3.变量分离型
应用3对一切实数x,关于x的不等式x4+ax2+1≥0恒成立,求字母a的取值范围.
提示:从所给不等式中解出a,再利用均值不等式求解.专题一专题二专题三专题四专题五专题六专题五 线性规划问题
1.二元一次不等式组表示的平面区域的作法是:画线、定侧、取交集.画线要分虚、实线,定侧可用特殊点检验.
2.简单的线性规划问题应注意两点:(1)准确作图,尤其注意目标函数所表示的直线与过可行域边界的直线的斜率关系;(2)整数解问题,整数解不一定在可行域边界或顶点上.
3.当目标函数不是线性情况时,解决问题的关键是利用图形的直观性,第一,要准确作出可行域;第二,要抓住目标函数z=f(x,y)中z的几何意义.专题一专题二专题三专题四专题五专题六应用1在平面直角坐标系中,若不等式组 (a为常数)
所表示的平面区域的面积等于2,则a的值为( )
A.-5 B.1 C.2 D.3解析:不等式组所表示的可行域如图阴影部分. 专题一专题二专题三专题四专题五专题六因为△ABC的面积为2,且a>-1(若a≤-1,则满足题意的可行域不存在),
所以S△ABC= (a+1)×1=2.解得a=3.
答案:D专题一专题二专题三专题四专题五专题六应用2已知x,y满足线性约束条件
分别求:
(1)u=4x-3y的最大值和最小值;
(2)w=4x+3y的最大值和最小值;
(3)z=x2+y2的最大值和最小值;专题一专题二专题三专题四专题五专题六解:已知不等式组为 在同一直角坐标系中,作直线
x-2y+7=0,4x-3y-12=0和x+2y-3=0,再根据不等式组确定可行域,如图阴影部分.专题一专题二专题三专题四专题五专题六专题一专题二专题三专题四专题五专题六专题一专题二专题三专题四专题五专题六专题六 不等式与函数、方程的综合问题
1.利用不等式的性质、不等式的证明方法、解不等式等知识可以解决函数中的有关问题,主要体现在:利用不等式求函数的定义域、值域、最值以及证明函数单调性等.
2.利用函数、方程、不等式之间的关系,可解决一元二次方程根的分布及相关的不等式问题.专题一专题二专题三专题四专题五专题六应用1当m为何值时,关于x的方程(m+1)x2+2(2m+1)x+(1-3m)=0.
(1)有两个异号实根;
(2)有两个实根,且它们的和为非负数.
提示:因为方程有两个实根,所以一定为一元二次方程,故m+1≠0,然后再按照一元二次方程根的情况与系数的关系进行求解.
解:(1)有两个异号实根,等价于不等式组专题一专题二专题三专题四专题五专题六(2)有两个实根,且它们的和为非负数,等价于不等式组 专题一专题二专题三专题四专题五专题六应用2已知函数f(x)=log3 的定义域为R,值域为[0,2],求m,n的值.
提示:将定义域问题转化为不等式恒成立问题,即转化为mx2+8x+n>0的解集为R.因为x∈R,所以Δ=82-4(m-y)(n-y)≥0,
即y2-(m+n)y+mn-16≤0.①专题一专题二专题三专题四专题五专题六由题意知f(x)∈[0,2],则y∈[1,9].
即关于y的不等式①的解集为[1,9].123456781(山东高考)已知实数x,y满足axy.
又因为函数f(x)=x3在R上递增,
所以f(x)>f(y),即x3>y3.
答案:D123456782(全国高考)设集合M={x|x2-3x-4<0},N={x|0≤x≤5},则M∩N=( )
A.(0,4] B.[0,4)
C.[-1,0) D.(-1,0]
解析:∵M={x|x2-3x-4<0}={x|-1N={x|0≤x≤5},
∴M∩N={x|0≤x<4}=[0,4),选B.
答案:B123456783(安徽高考)x,y满足约束条件 若z=y-ax取得最大值
的最优解不唯一,则实数a的值为( )
A. 或-1 B.2或
C.2或1 D.2或-1
解析:画出x,y约束条件限定的可行域,如图阴影部分所示,
由z=y-ax得y=ax+z,
当直线y=ax与直线2x-y+2=0或直线x+y-2=0平行时,符合题意,则a=2或-1.
答案:D123456784(北京高考)若x,y满足 且z=y-x的最小值为-4,则k的值为( )所表示的平面区域,作出目标函数取得最小值 -4时对应的直线y-x=-4,即x-y-4=0.显然z的几何 意义为目标函数对应直线x-y+z=0在x轴上的截 距的相反数,故该直线与x轴的交点(4,0)必为可 行域的顶点,又kx-y+2=0恒过点(0,2),答案:D 123456785(辽宁高考)已知定义在[0,1]上的函数f(x)满足:
①f(0)=f(1)=0;
②对所有x,y∈[0,1],且x≠y,有|f(x)-f(y)|< |x-y|.
若对所有x,y∈[0,1],|f(x)-f(y)|则实数a的取值范围是 .?解析:作出题中线性规划条件满足的可行域如图阴影部分所示,令z=ax+y,即y=-ax+z.12345678
函数是中学数学中的重点内容之一,它贯穿于中学数学教学的始终,而利用函数的图象能直观、准确、迅速地分析研究函数的性质或解决与函数有关的问题,因此,函数图象是高考考查的重点内容,在历年高考中都有涉及.
函数图象形象地显示了函数的性质,为研究数量关系提供了形的直观性,它是探求解题路径、获得问题结果的重要工具,在解方程或不等式时,特别是非常规的方程或不等式,有时需要画出图象,利用数形结合能起到十分快捷的效果.专题一专题二专题三专题四专题五专题六应用1已知函数f(x)= 若方程f(x)=k无实根,则实数
k的取值范围是( )提示:所给的函数f(x)是分段函数,而方程f(x)=k无实数根,可利用数形结合法转化为函数图象无交点.专题一专题二专题三专题四专题五专题六解析:在同一坐标系内作出y=f(x)与y=k的图象,如图所示, 答案:C 专题一专题二专题三专题四专题五专题六应用2已知a,b,c依次是方程2x+x=0,log2x=2-x和 =x的实数根,则a,b,c的大小关系是 .?
提示:构造常见的初等函数,利用函数的图象可解决问题.
解析:由2x+x=0,得2x=-x,设函数y1=2x,y2=-x,分别作出它们的图象,如图①,两图象交点的横坐标为a,可得a<0,同理,对于方程log2x=2-x,可得图②,得1
(1)解一元二次不等式,画出其对应的二次函数图象,来确定解集.
(2)解高次不等式常用穿根法.
(3)分式不等式利用不等式的性质将其转化为整式不等式(组)求解.
(4)解含有指数、对数的不等式时,利用指数与对数函数的单调性,将指数、对数不等式转化成与之等价的不等式(组)求解.专题一专题二专题三专题四专题五专题六应用1求解下列不等式:
(1)-x2+2x+3<0;
(2)x3+2x2-3x>0;提示:(1)注意解一元二次不等式的几个步骤.
(2)穿根法求解.
(3)转化为整式不等式,注意分母不为0.
(4)对数不等式,真数大于0.
解:(1)因为-x2+2x+3<0,所以x2-2x-3>0.
又方程x2-2x-3=0的两根为x1=-1,x2=3,
所以原不等式的解集为{x|x>3或x<-1}.专题一专题二专题三专题四专题五专题六(2)由x3+2x2-3x=x(x2+2x-3)=x(x+3)(x-1),可令f(x)=x(x-1)(x+3),
因为f(x)=0的根为-3,0,1,
所以由穿根法(如图),得不等式x3+2x2-3x>0的解集为{x|x>1或-3
如图,由穿根法得原不等式的解集为{x|-2≤x≤1或x>2}.专题一专题二专题三专题四专题五专题六专题一专题二专题三专题四专题五专题六应用2解关于x的不等式(x-2)(ax-2)>0.
提示:二次项系数为a,需对a的正负进行讨论;还要对根的大小进行讨论,两者要同时进行.
解:(1)当a=0时,原不等式化为(x-2)·(-2)>0,即x-2<0,所以x<2.专题一专题二专题三专题四专题五专题六综上所述,不等式的解集为
当a=0时,{x|x<2};
当a=1时,{x|x≠2};专题一专题二专题三专题四专题五专题六专题三 利用均值不等式求最值的常用方法
均值不等式是一个重要的不等式,利用它可以求解某些函数最值问题.对于有些题目,可以直接利用均值不等式求解.但是有些题目必须进行必要的变形才能利用均值不等式求解.常见的变形方法为配凑法、整体代换法等.下面介绍一些常用的变形方法.
1.凑系数
应用1已知0
所以x+y的最小值为36.专题一专题二专题三专题四专题五专题六专题四 不等式恒成立问题
恒成立问题,涉及一次函数、二次函数的性质、图象,渗透着换元、化归、数形结合、函数与方程等思想方法,是很综合的一个题型,也是历年高考的一个热点.变量分离法和数形结合的方法比较常用,数形结合的方法较简单.当然还有其他的解决方法,如赋值法、根据对称性等.专题一专题二专题三专题四专题五专题六1.一次函数型
应用1对于满足|p|≤2的所有实数p,求使关于x的不等式x2+px+1>p+2x恒成立的x的取值范围.
提示:在不等式中出现了两个字母:x和p,关键在于该把哪个字母看成是变量.本题可将p视作变量,则上述问题即可转化为在[-2,2]内关于p的一次函数大于0恒成立的问题.
解:原不等式即(x-1)p+x2-2x+1>0,设f(p)=(x-1)p+x2-2x+1,则f(p)在[-2,2]上恒大于0,故有:专题一专题二专题三专题四专题五专题六2.二次函数型
应用2设f(x)=x2-2ax+2,当x∈[-1,+∞)时,都有f(x)≥a恒成立,求a的取值范围.
提示:题目中要证明f(x)≥a恒成立,若把a移到等号的左边,则把原题转化成左边二次函数在区间[-1,+∞)内恒大于0的问题,就可以利用函数的图象解决了.
解:设F(x)=f(x)-a=x2-2ax+2-a.
(1)当Δ=4a2-4(2-a)=4(a-1)(a+2) ≤0,即-2≤a≤1时,对一切x∈[-1,+∞),F(x)≥0恒成立;专题一专题二专题三专题四专题五专题六(2)当Δ=4(a-1)(a+2) >0时,由图可得以下充要条件:
得-3≤a<-2.
综上可得a的取值范围为[-3,1].专题一专题二专题三专题四专题五专题六3.变量分离型
应用3对一切实数x,关于x的不等式x4+ax2+1≥0恒成立,求字母a的取值范围.
提示:从所给不等式中解出a,再利用均值不等式求解.专题一专题二专题三专题四专题五专题六专题五 线性规划问题
1.二元一次不等式组表示的平面区域的作法是:画线、定侧、取交集.画线要分虚、实线,定侧可用特殊点检验.
2.简单的线性规划问题应注意两点:(1)准确作图,尤其注意目标函数所表示的直线与过可行域边界的直线的斜率关系;(2)整数解问题,整数解不一定在可行域边界或顶点上.
3.当目标函数不是线性情况时,解决问题的关键是利用图形的直观性,第一,要准确作出可行域;第二,要抓住目标函数z=f(x,y)中z的几何意义.专题一专题二专题三专题四专题五专题六应用1在平面直角坐标系中,若不等式组 (a为常数)
所表示的平面区域的面积等于2,则a的值为( )
A.-5 B.1 C.2 D.3解析:不等式组所表示的可行域如图阴影部分. 专题一专题二专题三专题四专题五专题六因为△ABC的面积为2,且a>-1(若a≤-1,则满足题意的可行域不存在),
所以S△ABC= (a+1)×1=2.解得a=3.
答案:D专题一专题二专题三专题四专题五专题六应用2已知x,y满足线性约束条件
分别求:
(1)u=4x-3y的最大值和最小值;
(2)w=4x+3y的最大值和最小值;
(3)z=x2+y2的最大值和最小值;专题一专题二专题三专题四专题五专题六解:已知不等式组为 在同一直角坐标系中,作直线
x-2y+7=0,4x-3y-12=0和x+2y-3=0,再根据不等式组确定可行域,如图阴影部分.专题一专题二专题三专题四专题五专题六专题一专题二专题三专题四专题五专题六专题一专题二专题三专题四专题五专题六专题六 不等式与函数、方程的综合问题
1.利用不等式的性质、不等式的证明方法、解不等式等知识可以解决函数中的有关问题,主要体现在:利用不等式求函数的定义域、值域、最值以及证明函数单调性等.
2.利用函数、方程、不等式之间的关系,可解决一元二次方程根的分布及相关的不等式问题.专题一专题二专题三专题四专题五专题六应用1当m为何值时,关于x的方程(m+1)x2+2(2m+1)x+(1-3m)=0.
(1)有两个异号实根;
(2)有两个实根,且它们的和为非负数.
提示:因为方程有两个实根,所以一定为一元二次方程,故m+1≠0,然后再按照一元二次方程根的情况与系数的关系进行求解.
解:(1)有两个异号实根,等价于不等式组专题一专题二专题三专题四专题五专题六(2)有两个实根,且它们的和为非负数,等价于不等式组 专题一专题二专题三专题四专题五专题六应用2已知函数f(x)=log3 的定义域为R,值域为[0,2],求m,n的值.
提示:将定义域问题转化为不等式恒成立问题,即转化为mx2+8x+n>0的解集为R.因为x∈R,所以Δ=82-4(m-y)(n-y)≥0,
即y2-(m+n)y+mn-16≤0.①专题一专题二专题三专题四专题五专题六由题意知f(x)∈[0,2],则y∈[1,9].
即关于y的不等式①的解集为[1,9].123456781(山东高考)已知实数x,y满足ax
又因为函数f(x)=x3在R上递增,
所以f(x)>f(y),即x3>y3.
答案:D123456782(全国高考)设集合M={x|x2-3x-4<0},N={x|0≤x≤5},则M∩N=( )
A.(0,4] B.[0,4)
C.[-1,0) D.(-1,0]
解析:∵M={x|x2-3x-4<0}={x|-1
∴M∩N={x|0≤x<4}=[0,4),选B.
答案:B123456783(安徽高考)x,y满足约束条件 若z=y-ax取得最大值
的最优解不唯一,则实数a的值为( )
A. 或-1 B.2或
C.2或1 D.2或-1
解析:画出x,y约束条件限定的可行域,如图阴影部分所示,
由z=y-ax得y=ax+z,
当直线y=ax与直线2x-y+2=0或直线x+y-2=0平行时,符合题意,则a=2或-1.
答案:D123456784(北京高考)若x,y满足 且z=y-x的最小值为-4,则k的值为( )所表示的平面区域,作出目标函数取得最小值 -4时对应的直线y-x=-4,即x-y-4=0.显然z的几何 意义为目标函数对应直线x-y+z=0在x轴上的截 距的相反数,故该直线与x轴的交点(4,0)必为可 行域的顶点,又kx-y+2=0恒过点(0,2),答案:D 123456785(辽宁高考)已知定义在[0,1]上的函数f(x)满足:
①f(0)=f(1)=0;
②对所有x,y∈[0,1],且x≠y,有|f(x)-f(y)|< |x-y|.
若对所有x,y∈[0,1],|f(x)-f(y)|
