高中数学新人教B版必修5课件:第一章解三角形1.1.1正弦定理(34张)
文档属性
| 名称 | 高中数学新人教B版必修5课件:第一章解三角形1.1.1正弦定理(34张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-21 12:57:11 | ||
图片预览









文档简介
课件34张PPT。第一章 解三角形1.1 正弦定理和余弦定理1.1.1 正弦定理1.理解正弦定理及其相关变式的推导过程.
2.掌握正弦定理,并初步学会用正弦定理解决简单的三角形度量问题.
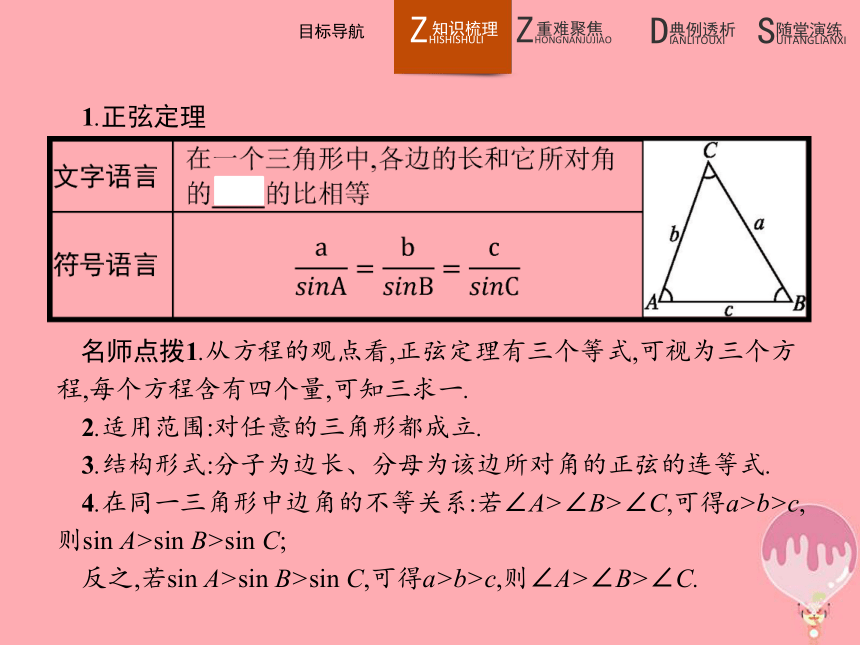
3.依据正弦定理判断三角形的形状.1.正弦定理 名师点拨1.从方程的观点看,正弦定理有三个等式,可视为三个方程,每个方程含有四个量,可知三求一.
2.适用范围:对任意的三角形都成立.
3.结构形式:分子为边长、分母为该边所对角的正弦的连等式.
4.在同一三角形中边角的不等关系:若∠A>∠B>∠C,可得a>b>c,则sin A>sin B>sin C;
反之,若sin A>sin B>sin C,可得a>b>c,则∠A>∠B>∠C.【做一做1-1】 在△ABC中,一定成立的等式有( )
A.asin A=bsin B B.asin B=bsin A
C.acos A=bcos B D.acos B=bcos A
答案:B
【做一做1-2】 在△ABC中,已知AC=2,BC=3,sin A= ,则sin B=( )答案:A 2.正弦定理的适用范围
利用正弦定理,可解决两类解三角形的问题:
(1)已知两角和任一边,求其他的边和角;
(2)已知两边和其中一边的对角,首先求另一边的对角,然后求出其他的边和角.
【做一做2】 在△ABC中,已知a= ,b=4,∠A=30°,则∠B= .?由b>a,得∠B=60°或∠B=120°. 答案:60°或120° 3.解三角形
解三角形是指由三角形的六个元素(三条边和三个角)中的三个元素(至少有一个是边),求其余三个未知元素的过程.一二一、判断三角形解的个数
剖析:(1)代数法
在△ABC中,已知a,b,∠A,由正弦定理可得sin B= sin A=m.
①当m>1时,这样的∠B不存在,即三角形无解.
②当m=1时,∠B=90°,若∠A<90°,则三角形有一解,否则无解.
③当m<1时,满足sin B=m的角有两个,其中设锐角为α,钝角为β,则当∠A+α≥180°时,三角形无解;当∠A+α<180°,且∠A+β<180°时,有两解;当∠A+α<180°,且∠A+β≥180°时,有一解.一二(2)几何法
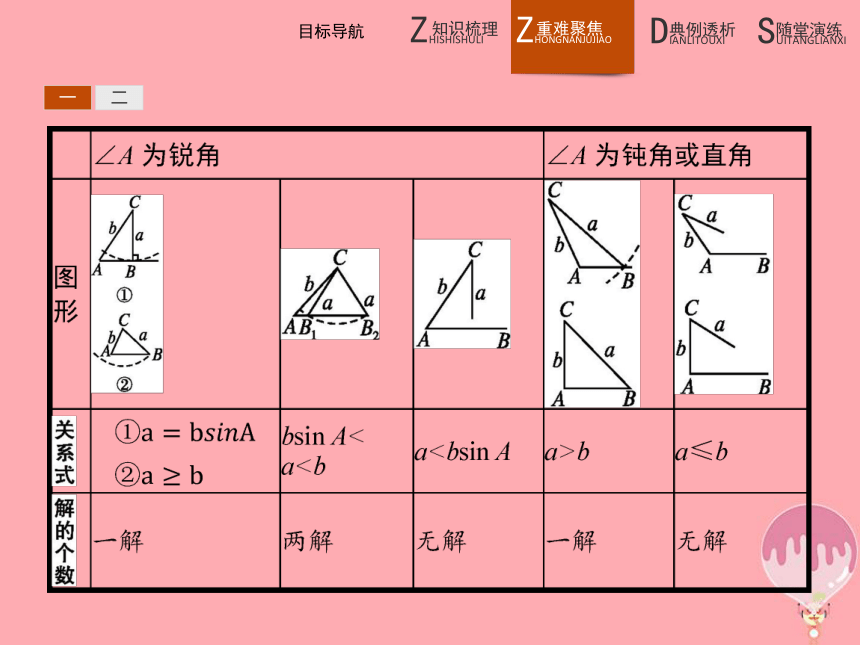
根据条件中∠A的大小,分为锐角、直角、钝角三种情况,通过几何作图,得出解的情况.作出已知∠A,以点A为圆心,边长b为半径画弧交∠A的一边于点C.使未知的边AB水平,顶点C在边AB上方,以点C为圆心,边长a为半径作圆,该圆与射线AB交点的个数,即为解的个数,如表所示:一二一二二、教材中的“探索与研究”
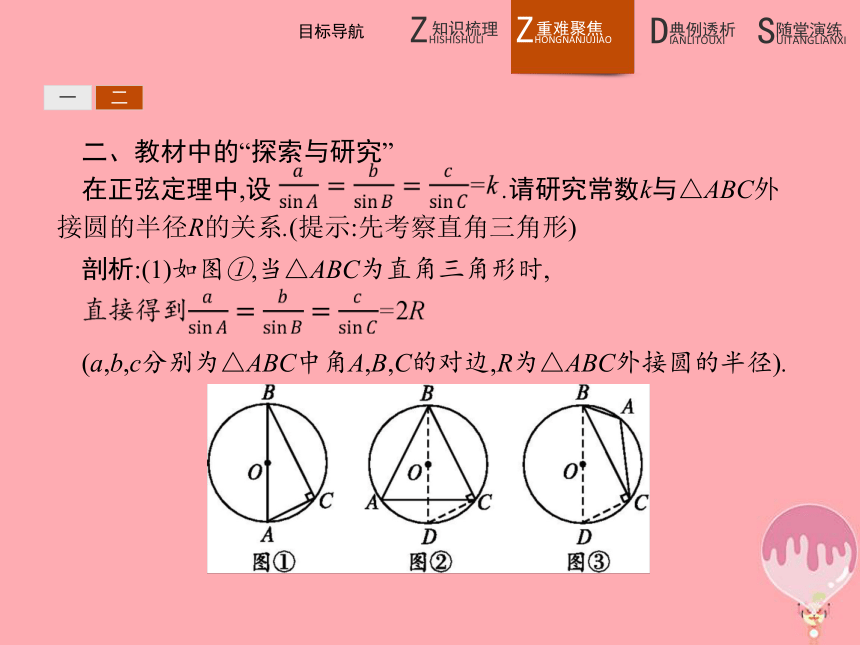
在正弦定理中,设 .请研究常数k与△ABC外接圆的半径R的关系.(提示:先考察直角三角形)剖析:(1)如图①,当△ABC为直角三角形时, (a,b,c分别为△ABC中角A,B,C的对边,R为△ABC外接圆的半径).一二(2)如图②,当△ABC为锐角三角形时,连接BO并延长交圆O于点D,连接CD.
因为∠A=∠D,(3)如图③,当△ABC为钝角三角形,且∠A为钝角时,连接BO并延长交圆O于点D,连接CD,∠A=180°-∠D,一二归纳总结根据上述关系式可得到正弦定理的常用变式:
(1)asin B=bsin A;asin C=csin A;bsin C=csin B.(4)a∶b∶c=sin A∶sin B∶sin C.
(5)边化角公式:a=2Rsin A,b=2Rsin B,c=2Rsin C.题型一题型二题型三题型四解三角形
【例1】 已知在△ABC中,c=10,∠A=45°,∠C=30°,求a,b和∠B.
分析:当知道两个角时,即可知道第三个角,所以若再知道三边中任意一边,就可解这个三角形.题型一题型二题型三题型四【变式训练1】已知在△ABC中,a=10,∠B=60°,∠C=45°,则c等于( )解析:∵∠A+∠B+∠C=180°,
∴∠A=180°-∠B-∠C=180°-60°-45°=75°.答案:B 题型一题型二题型三题型四分析:已知两边和其中一边的对角的解三角形问题可运用正弦定理来求解,但应注意解的个数.【例2】 在△ABC中,已知a= ,b= ,∠B=45°,求∠A,∠C和c.题型一题型二题型三题型四题型一题型二题型三题型四反思已知两边和其中一边的对角,求另一边的对角及其他的角和边的方法步骤:先由正弦定理求得已知边的对角,再利用内角和公式求得第三角,最后求得第三边.解答此类问题应注意对解的个数的讨论.题型一题型二题型三题型四【变式训练2】 根据下列条件,判断三角形解的情况,其中正确的是( )
A.a=8,b=16,∠A=30°,有两解
B.a=18,b=20,∠A=60°,有一解
C.a=5,b=2,∠A=90°,无解
D.a=30,b=25,∠A=150°,有一解
解析:A中,a=bsin A,故有一解;
B中,bsin A=20·sin 60°=10C中,∠A为直角,且a>b,故有一解;
D中,a>b,∠A为钝角,故有一解.
因此正确答案为D.
答案:D题型一题型二题型四题型三判断三角形的形状
【例3】 在△ABC中,∠A,∠B,∠C的对边分别为a,b,c,且
,试判断△ABC的形状.分析:将式中的a,b,c分别用2Rsin A,2Rsin B,2Rsin C(R为△ABC外接圆半径)来代替是解决本题的关键.所以tan A=tan B=tan C.
又因为∠A,∠B,∠C是△ABC的内角,
所以∠A=∠B=∠C,
所以△ABC是等边三角形.题型一题型二题型四题型三反思已知三角形中的边角关系式,判断三角形的形状,有两种思路:其一,先化边为角,再进行三角恒等变换求出三个角之间的关系;其二,先化角为边,再进行代数恒等变换求出三条边之间的关系.题型一题型二题型四题型三【变式训练3】 已知在△ABC中,∠A,∠B所对的边分别是a和b,若acos B=bcos A,试判断△ABC的形状.得a=2Rsin A,b=2Rsin B.
又acos B=bcos A,
故sin Acos B=sin Bcos A,
即sin(A-B)=0.
由-π<∠A-∠B<π,知∠A-∠B=0,即∠A=∠B.
故△ABC为等腰三角形.题型一题型二题型三题型四三角形面积公式的应用
【例4】 在△ABC中,c=2 ,a>b,∠C= ,且有tan A·tan B=6,试求a,b及此时三角形的面积.分析:由已知可求出tan A+tan B的值,这样便可求出tan A,tan B的值,只要求出sin A,sin B,利用正弦定理便可求出a,b.题型一题型二题型三题型四解:∵tan A+tan B=tan(A+B)(1-tan Atan B)
=-tan C(1-tan Atan B)=-tan (1-6)=5,
又tan A·tan B=6,且a>b,
∴tan A>tan B,
∴tan A=3,tan B=2.题型一题型二题型三题型四反思在求三角形的面积时,应注意运用三角形中的常见性质以及两角和与差的正、余弦公式.当已知条件不满足三角形面积公式的条件时, 一般可通过正弦定理求出所需要的量,再计算三角形的面积.题型一题型二题型三题型四【变式训练4】 在△ABC中,∠B= ,求△ABC的面积.题型一题型二题型三题型四易错辨析
易错点:忽视角的取值范围而致误
【例5】 在△ABC中,若a2tan B=b2tan A,试判断△ABC的形状.整理得sin Acos A=sin Bcos B,
∴sin 2A=sin 2B,
∴2∠A=2∠B,
故△ABC为等腰三角形.题型一题型二题型三题型四错因分析:在判断三角形形状时忽视内角∠ A, ∠ B的范围在(0,π),2∠A,2∠B的范围应为(0,2π),所以由sin 2A=sin 2B求解时应有2∠A=2∠B或2∠A=π-2∠B两种情况,即∠A=∠B或∠A+∠B= .正解:∵a2tan B=b2tan A,
又由正弦定理得a=2Rsin A,b=2Rsin B,∴sin Acos A=sin Bcos B.
即sin 2A=sin 2B.
∵0<2∠A<2π,0<2∠B<2π,
∴2∠A=2∠B或2∠A+2∠B=π,
即∠A=∠B或∠A+∠B= .1 2 3 4 51在△ABC中,已知a=3,b=5,sin A= ,则sin B=( ) 答案:B 1 2 3 4 52在△ABC中,根据下列条件解三角形,其中有两解的是 ( )
A.b=10,∠A=45°,∠C=70°
B.a=30,b=25,∠A=150°
C.a=7,b=8,∠A=98°
D.a=14,b=16,∠A=45°
解析:对于A项,由三角形全等的判定知识知只有一解;
对于B项,因为a>b,所以∠A>∠B.
又∠A=150°,所以只有一解;
对于C项,因为a而∠A=98°,所以无解;所以bsin A答案:D3在△ABC中,已知∠A=60°,a=3 ,c=6,则△ABC的面积为( )1 2 3 4 5解析:∵∠A=60°,a=3 ,c=6,
∴c∴∠C<∠A,
∴∠C为锐角.答案:A 1 2 3 4 54在△ABC中, ∠A, ∠B, ∠C所对的边长分别为a,b,c.若∠C=120°,c= a,则a与b的大小关系是 .?∴∠A>30°.
∴∠B=180°-120°-∠A<30°.
∴∠A>∠B.∴a>b.
答案:a>b1 2 3 4 55在△ABC中,已知 ,试判断△ABC的形状. 所以sin Acos A=sin Bcos B,
即2sin Acos A=2sin Bcos B,
所以sin 2A=sin 2B.
因为∠A,∠B为三角形的内角,
所以2∠A=2∠B或2∠A+2∠B=π,所以b≠a,所以∠B≠∠A,
2.掌握正弦定理,并初步学会用正弦定理解决简单的三角形度量问题.
3.依据正弦定理判断三角形的形状.1.正弦定理 名师点拨1.从方程的观点看,正弦定理有三个等式,可视为三个方程,每个方程含有四个量,可知三求一.
2.适用范围:对任意的三角形都成立.
3.结构形式:分子为边长、分母为该边所对角的正弦的连等式.
4.在同一三角形中边角的不等关系:若∠A>∠B>∠C,可得a>b>c,则sin A>sin B>sin C;
反之,若sin A>sin B>sin C,可得a>b>c,则∠A>∠B>∠C.【做一做1-1】 在△ABC中,一定成立的等式有( )
A.asin A=bsin B B.asin B=bsin A
C.acos A=bcos B D.acos B=bcos A
答案:B
【做一做1-2】 在△ABC中,已知AC=2,BC=3,sin A= ,则sin B=( )答案:A 2.正弦定理的适用范围
利用正弦定理,可解决两类解三角形的问题:
(1)已知两角和任一边,求其他的边和角;
(2)已知两边和其中一边的对角,首先求另一边的对角,然后求出其他的边和角.
【做一做2】 在△ABC中,已知a= ,b=4,∠A=30°,则∠B= .?由b>a,得∠B=60°或∠B=120°. 答案:60°或120° 3.解三角形
解三角形是指由三角形的六个元素(三条边和三个角)中的三个元素(至少有一个是边),求其余三个未知元素的过程.一二一、判断三角形解的个数
剖析:(1)代数法
在△ABC中,已知a,b,∠A,由正弦定理可得sin B= sin A=m.
①当m>1时,这样的∠B不存在,即三角形无解.
②当m=1时,∠B=90°,若∠A<90°,则三角形有一解,否则无解.
③当m<1时,满足sin B=m的角有两个,其中设锐角为α,钝角为β,则当∠A+α≥180°时,三角形无解;当∠A+α<180°,且∠A+β<180°时,有两解;当∠A+α<180°,且∠A+β≥180°时,有一解.一二(2)几何法
根据条件中∠A的大小,分为锐角、直角、钝角三种情况,通过几何作图,得出解的情况.作出已知∠A,以点A为圆心,边长b为半径画弧交∠A的一边于点C.使未知的边AB水平,顶点C在边AB上方,以点C为圆心,边长a为半径作圆,该圆与射线AB交点的个数,即为解的个数,如表所示:一二一二二、教材中的“探索与研究”
在正弦定理中,设 .请研究常数k与△ABC外接圆的半径R的关系.(提示:先考察直角三角形)剖析:(1)如图①,当△ABC为直角三角形时, (a,b,c分别为△ABC中角A,B,C的对边,R为△ABC外接圆的半径).一二(2)如图②,当△ABC为锐角三角形时,连接BO并延长交圆O于点D,连接CD.
因为∠A=∠D,(3)如图③,当△ABC为钝角三角形,且∠A为钝角时,连接BO并延长交圆O于点D,连接CD,∠A=180°-∠D,一二归纳总结根据上述关系式可得到正弦定理的常用变式:
(1)asin B=bsin A;asin C=csin A;bsin C=csin B.(4)a∶b∶c=sin A∶sin B∶sin C.
(5)边化角公式:a=2Rsin A,b=2Rsin B,c=2Rsin C.题型一题型二题型三题型四解三角形
【例1】 已知在△ABC中,c=10,∠A=45°,∠C=30°,求a,b和∠B.
分析:当知道两个角时,即可知道第三个角,所以若再知道三边中任意一边,就可解这个三角形.题型一题型二题型三题型四【变式训练1】已知在△ABC中,a=10,∠B=60°,∠C=45°,则c等于( )解析:∵∠A+∠B+∠C=180°,
∴∠A=180°-∠B-∠C=180°-60°-45°=75°.答案:B 题型一题型二题型三题型四分析:已知两边和其中一边的对角的解三角形问题可运用正弦定理来求解,但应注意解的个数.【例2】 在△ABC中,已知a= ,b= ,∠B=45°,求∠A,∠C和c.题型一题型二题型三题型四题型一题型二题型三题型四反思已知两边和其中一边的对角,求另一边的对角及其他的角和边的方法步骤:先由正弦定理求得已知边的对角,再利用内角和公式求得第三角,最后求得第三边.解答此类问题应注意对解的个数的讨论.题型一题型二题型三题型四【变式训练2】 根据下列条件,判断三角形解的情况,其中正确的是( )
A.a=8,b=16,∠A=30°,有两解
B.a=18,b=20,∠A=60°,有一解
C.a=5,b=2,∠A=90°,无解
D.a=30,b=25,∠A=150°,有一解
解析:A中,a=bsin A,故有一解;
B中,bsin A=20·sin 60°=10
D中,a>b,∠A为钝角,故有一解.
因此正确答案为D.
答案:D题型一题型二题型四题型三判断三角形的形状
【例3】 在△ABC中,∠A,∠B,∠C的对边分别为a,b,c,且
,试判断△ABC的形状.分析:将式中的a,b,c分别用2Rsin A,2Rsin B,2Rsin C(R为△ABC外接圆半径)来代替是解决本题的关键.所以tan A=tan B=tan C.
又因为∠A,∠B,∠C是△ABC的内角,
所以∠A=∠B=∠C,
所以△ABC是等边三角形.题型一题型二题型四题型三反思已知三角形中的边角关系式,判断三角形的形状,有两种思路:其一,先化边为角,再进行三角恒等变换求出三个角之间的关系;其二,先化角为边,再进行代数恒等变换求出三条边之间的关系.题型一题型二题型四题型三【变式训练3】 已知在△ABC中,∠A,∠B所对的边分别是a和b,若acos B=bcos A,试判断△ABC的形状.得a=2Rsin A,b=2Rsin B.
又acos B=bcos A,
故sin Acos B=sin Bcos A,
即sin(A-B)=0.
由-π<∠A-∠B<π,知∠A-∠B=0,即∠A=∠B.
故△ABC为等腰三角形.题型一题型二题型三题型四三角形面积公式的应用
【例4】 在△ABC中,c=2 ,a>b,∠C= ,且有tan A·tan B=6,试求a,b及此时三角形的面积.分析:由已知可求出tan A+tan B的值,这样便可求出tan A,tan B的值,只要求出sin A,sin B,利用正弦定理便可求出a,b.题型一题型二题型三题型四解:∵tan A+tan B=tan(A+B)(1-tan Atan B)
=-tan C(1-tan Atan B)=-tan (1-6)=5,
又tan A·tan B=6,且a>b,
∴tan A>tan B,
∴tan A=3,tan B=2.题型一题型二题型三题型四反思在求三角形的面积时,应注意运用三角形中的常见性质以及两角和与差的正、余弦公式.当已知条件不满足三角形面积公式的条件时, 一般可通过正弦定理求出所需要的量,再计算三角形的面积.题型一题型二题型三题型四【变式训练4】 在△ABC中,∠B= ,求△ABC的面积.题型一题型二题型三题型四易错辨析
易错点:忽视角的取值范围而致误
【例5】 在△ABC中,若a2tan B=b2tan A,试判断△ABC的形状.整理得sin Acos A=sin Bcos B,
∴sin 2A=sin 2B,
∴2∠A=2∠B,
故△ABC为等腰三角形.题型一题型二题型三题型四错因分析:在判断三角形形状时忽视内角∠ A, ∠ B的范围在(0,π),2∠A,2∠B的范围应为(0,2π),所以由sin 2A=sin 2B求解时应有2∠A=2∠B或2∠A=π-2∠B两种情况,即∠A=∠B或∠A+∠B= .正解:∵a2tan B=b2tan A,
又由正弦定理得a=2Rsin A,b=2Rsin B,∴sin Acos A=sin Bcos B.
即sin 2A=sin 2B.
∵0<2∠A<2π,0<2∠B<2π,
∴2∠A=2∠B或2∠A+2∠B=π,
即∠A=∠B或∠A+∠B= .1 2 3 4 51在△ABC中,已知a=3,b=5,sin A= ,则sin B=( ) 答案:B 1 2 3 4 52在△ABC中,根据下列条件解三角形,其中有两解的是 ( )
A.b=10,∠A=45°,∠C=70°
B.a=30,b=25,∠A=150°
C.a=7,b=8,∠A=98°
D.a=14,b=16,∠A=45°
解析:对于A项,由三角形全等的判定知识知只有一解;
对于B项,因为a>b,所以∠A>∠B.
又∠A=150°,所以只有一解;
对于C项,因为a
∴c
∴∠C为锐角.答案:A 1 2 3 4 54在△ABC中, ∠A, ∠B, ∠C所对的边长分别为a,b,c.若∠C=120°,c= a,则a与b的大小关系是 .?∴∠A>30°.
∴∠B=180°-120°-∠A<30°.
∴∠A>∠B.∴a>b.
答案:a>b1 2 3 4 55在△ABC中,已知 ,试判断△ABC的形状. 所以sin Acos A=sin Bcos B,
即2sin Acos A=2sin Bcos B,
所以sin 2A=sin 2B.
因为∠A,∠B为三角形的内角,
所以2∠A=2∠B或2∠A+2∠B=π,所以b≠a,所以∠B≠∠A,
