高中数学新人教B版选修2-1课件:第三章空间向量与立体几何本章整合(26张)
文档属性
| 名称 | 高中数学新人教B版选修2-1课件:第三章空间向量与立体几何本章整合(26张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-21 00:00:00 | ||
图片预览






文档简介
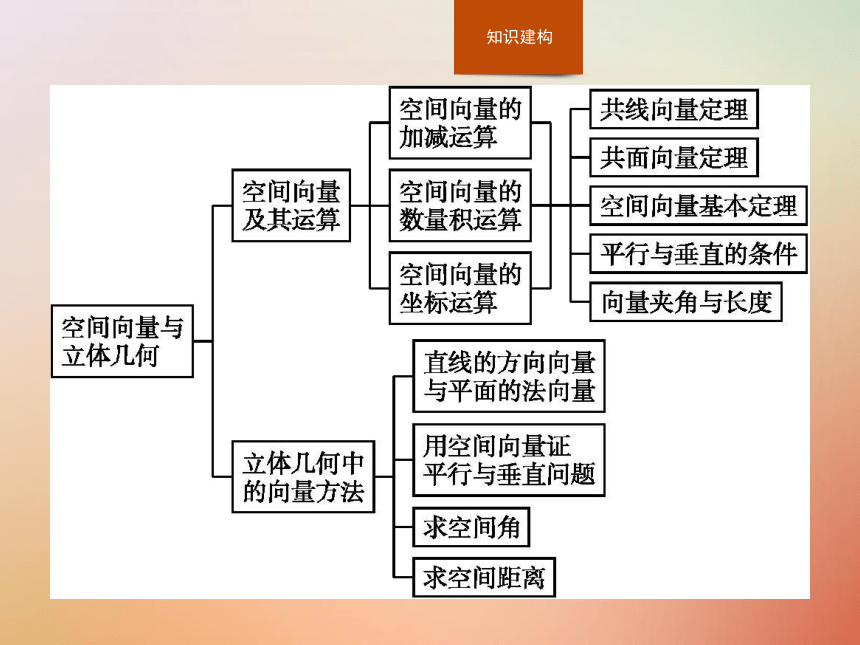
课件26张PPT。本 章 整 合专题一专题二专题三专题一 空间向量的概念
数学概念是数学体系的基础,准确掌握空间向量的有关概念是学好空间向量的关键.
注意概念的严密、精练、准确性,防止缺失概念中的某些条件或者忽略概念规定的特殊情况.专题一专题二专题三应用给出下列命题: ②若a·b<0,则是钝角;
③若a是直线l的方向向量,则λa(λ∈R)也是l的方向向量;
④非零向量a,b,c满足a与b,b与c,c与a都是共面向量,则a,b,c必共面.
其中错误命题的个数是( )
A.1 B.2
C.3 D.4专题一专题二专题三专题一专题二专题三专题二 空间向量与线面的位置关系
利用向量平行、向量垂直的条件,解决空间中的平行与垂直关系,将几何证明转化为纯代数运算,从而使问题得以简化.
(1)证明两条直线平行,只需证明这两条直线的方向向量是共线向量.
(2)证明线面平行的方法:
①证明直线的方向向量与平面的法向量垂直;
②证明能够在平面内找到一个向量与已知直线的方向向量共线;
③利用共面向量定理,即证明直线的方向向量与平面内的两个不共线向量是共面向量.
(3)证明面面平行的方法:
①转化为线线平行、线面平行处理;
②证明这两个平面的法向量是共线向量.专题一专题二专题三(4)证明线线垂直的方法是证明这两条直线的方向向量互相垂直.
(5)证明线面垂直的方法:
①证明直线的方向向量与平面的法向量是共线向量;
②证明直线与平面内的两个不共线的向量互相垂直.
(6)证明面面垂直的方法:
①转化为线线垂直、线面垂直处理;
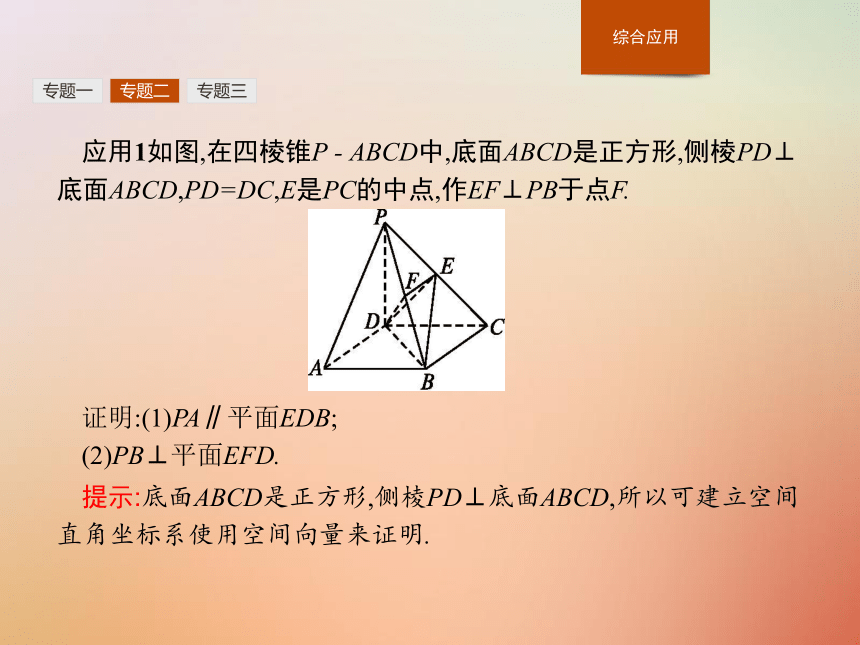
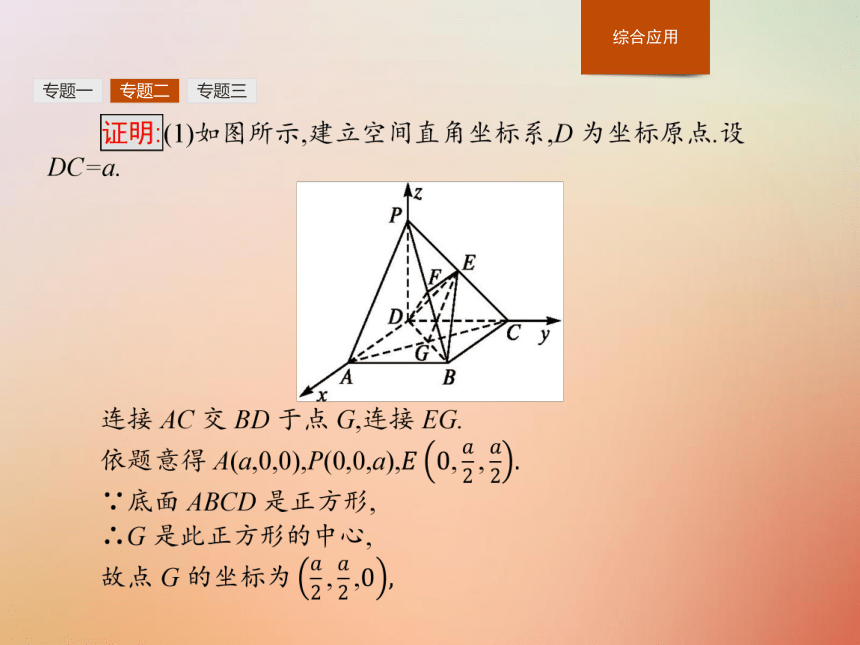
②证明两个平面的法向量互相垂直.专题一专题二专题三应用1如图,在四棱锥P - ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB于点F.证明:(1)PA∥平面EDB;
(2)PB⊥平面EFD.提示:底面ABCD是正方形,侧棱PD⊥底面ABCD,所以可建立空间直角坐标系使用空间向量来证明.专题一专题二专题三专题一专题二专题三专题一专题二专题三应用2在直三棱柱ABC - A1B1C1中,∠ACB=90°,AC=1,专题一专题二专题三专题一专题二专题三专题三 利用空间向量求空间的角与距离
利用向量求空间中的夹角及距离问题是高考的重点.解题的关键是会找直线的方向向量及平面的法向量,并用它们表示空间中的角及距离,所有的空间距离问题用向量求时,有着相同的表现形式.应加强理解,求角时,要弄清向量夹角与所求角的关系.
应用1在正方体ABCD - A1B1C1D1中,E,F分别为AA1,AB的中点,求EF和平面ACC1A1所成角的大小.
提示:已知正方体中有两两垂直的关系,故可考虑建系用法向量求解.专题一专题二专题三专题一专题二专题三提示:设CD的中点为O,可证明MO,BO,CD两两垂直,从而可用等积法、定义法求解或者建系用向量法来求解.专题一专题二专题三专题一专题二专题三专题一专题二专题三123?1231232.(安徽高考)如图,ABEDFC为多面体,平面ABED与平面ACFD垂直,点O在线段AD上,OA=1,OD=2,△OAB,△OAC,△ODE,△ODF都是正三角形.
?
(1)证明:直线BC∥EF;
(2)求棱锥F - OBED的体积.1231231233.(北京高考)如图,在四棱锥P - ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°.
?
(1)求证:BD⊥平面PAC;
(2)若PA=AB,求PB与AC所成角的余弦值;
(3)当平面PBC与平面PDC垂直时,求PA的长.
(1)证明:因为四边形ABCD是菱形,所以AC⊥BD.
又因为PA⊥平面ABCD,所以PA⊥BD.
所以BD⊥平面PAC.123123
数学概念是数学体系的基础,准确掌握空间向量的有关概念是学好空间向量的关键.
注意概念的严密、精练、准确性,防止缺失概念中的某些条件或者忽略概念规定的特殊情况.专题一专题二专题三应用给出下列命题: ②若a·b<0,则
③若a是直线l的方向向量,则λa(λ∈R)也是l的方向向量;
④非零向量a,b,c满足a与b,b与c,c与a都是共面向量,则a,b,c必共面.
其中错误命题的个数是( )
A.1 B.2
C.3 D.4专题一专题二专题三专题一专题二专题三专题二 空间向量与线面的位置关系
利用向量平行、向量垂直的条件,解决空间中的平行与垂直关系,将几何证明转化为纯代数运算,从而使问题得以简化.
(1)证明两条直线平行,只需证明这两条直线的方向向量是共线向量.
(2)证明线面平行的方法:
①证明直线的方向向量与平面的法向量垂直;
②证明能够在平面内找到一个向量与已知直线的方向向量共线;
③利用共面向量定理,即证明直线的方向向量与平面内的两个不共线向量是共面向量.
(3)证明面面平行的方法:
①转化为线线平行、线面平行处理;
②证明这两个平面的法向量是共线向量.专题一专题二专题三(4)证明线线垂直的方法是证明这两条直线的方向向量互相垂直.
(5)证明线面垂直的方法:
①证明直线的方向向量与平面的法向量是共线向量;
②证明直线与平面内的两个不共线的向量互相垂直.
(6)证明面面垂直的方法:
①转化为线线垂直、线面垂直处理;
②证明两个平面的法向量互相垂直.专题一专题二专题三应用1如图,在四棱锥P - ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB于点F.证明:(1)PA∥平面EDB;
(2)PB⊥平面EFD.提示:底面ABCD是正方形,侧棱PD⊥底面ABCD,所以可建立空间直角坐标系使用空间向量来证明.专题一专题二专题三专题一专题二专题三专题一专题二专题三应用2在直三棱柱ABC - A1B1C1中,∠ACB=90°,AC=1,专题一专题二专题三专题一专题二专题三专题三 利用空间向量求空间的角与距离
利用向量求空间中的夹角及距离问题是高考的重点.解题的关键是会找直线的方向向量及平面的法向量,并用它们表示空间中的角及距离,所有的空间距离问题用向量求时,有着相同的表现形式.应加强理解,求角时,要弄清向量夹角与所求角的关系.
应用1在正方体ABCD - A1B1C1D1中,E,F分别为AA1,AB的中点,求EF和平面ACC1A1所成角的大小.
提示:已知正方体中有两两垂直的关系,故可考虑建系用法向量求解.专题一专题二专题三专题一专题二专题三提示:设CD的中点为O,可证明MO,BO,CD两两垂直,从而可用等积法、定义法求解或者建系用向量法来求解.专题一专题二专题三专题一专题二专题三专题一专题二专题三123?1231232.(安徽高考)如图,ABEDFC为多面体,平面ABED与平面ACFD垂直,点O在线段AD上,OA=1,OD=2,△OAB,△OAC,△ODE,△ODF都是正三角形.
?
(1)证明:直线BC∥EF;
(2)求棱锥F - OBED的体积.1231231233.(北京高考)如图,在四棱锥P - ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°.
?
(1)求证:BD⊥平面PAC;
(2)若PA=AB,求PB与AC所成角的余弦值;
(3)当平面PBC与平面PDC垂直时,求PA的长.
(1)证明:因为四边形ABCD是菱形,所以AC⊥BD.
又因为PA⊥平面ABCD,所以PA⊥BD.
所以BD⊥平面PAC.123123
