人教版高中数学必修二知识讲解,巩固练习(教学资料,补习资料):专题2.2 直线、平面平行的判定及其性质
文档属性
| 名称 | 人教版高中数学必修二知识讲解,巩固练习(教学资料,补习资料):专题2.2 直线、平面平行的判定及其性质 |
|
|
| 格式 | zip | ||
| 文件大小 | 978.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-21 20:08:55 | ||
图片预览



文档简介
知识
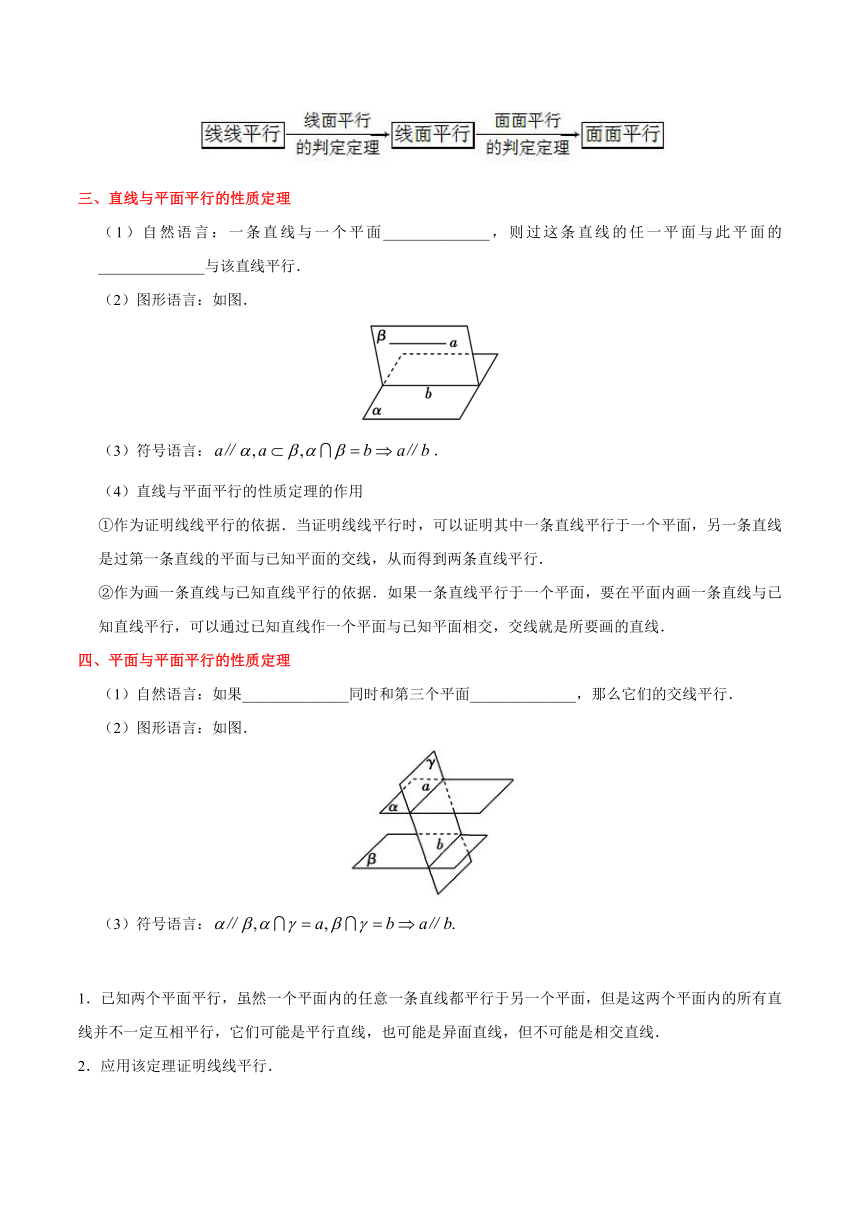
一、直线与平面平行的判定定理
语言文字
_______一条直线与此平面内的一条直线________,则该直线与此平面平行
图形语言
符号语言
a?α,b?α,且a∥b?a∥α
作用
证明直线与平面______________
二、平面与平面平行的判定定理
语言文字
一个平面内的两条________直线与另一个平面________,则这两个平面平行
图形语言
符号语言
a?β,b?β,__________,a∥α,b∥α?α∥β
作用
证明两个平面__________
1.要证明两平面平行,需要在其中一个平面内找到两条相交直线平行于另一个平面,注意“相交”二字不能丢.
2.可以通过证明线线平行来证明面面平行.
三、直线与平面平行的性质定理
(1)自然语言:一条直线与一个平面______________,则过这条直线的任一平面与此平面的______________与该直线平行.
(2)图形语言:如图.
(3)符号语言:.
(4)直线与平面平行的性质定理的作用
①作为证明线线平行的依据.当证明线线平行时,可以证明其中一条直线平行于一个平面,另一条直线是过第一条直线的平面与已知平面的交线,从而得到两条直线平行.
②作为画一条直线与已知直线平行的依据.如果一条直线平行于一个平面,要在平面内画一条直线与已知直线平行,可以通过已知直线作一个平面与已知平面相交,交线就是所要画的直线.
四、平面与平面平行的性质定理
(1)自然语言:如果______________同时和第三个平面______________,那么它们的交线平行.
(2)图形语言:如图.
(3)符号语言:
1.已知两个平面平行,虽然一个平面内的任意一条直线都平行于另一个平面,但是这两个平面内的所有直线并不一定互相平行,它们可能是平行直线,也可能是异面直线,但不可能是相交直线.
2.应用该定理证明线线平行.
五、两个平面平行的其他性质
(1)两个平面平行,其中一个平面内的任意一条直线都平行于另一个平面.
(2)夹在两个平行平面间的平行线段相等.
(3)经过平面外一点有且只有一个平面与已知平面平行.
(4)两条直线被三个平行平面所截,截得的对应线段成比例.
(5)如果两个平面分别平行于第三个平面,那么这两个平面互相平行.
知识参考答案:
重点
重点
1.直线与平面平行的判定、平面与平面平行的判定;
2.掌握直线与平面平行的性质定理,明确由线面平行可推出线线平行;
3.掌握平面与平面平行的性质定理,并会应用性质定理解决问题.
难点
1.线面平行、面面平行的综合应用;
2.掌握直线与直线、直线与平面、平面与平面之间的平行关系的相互转化.
易错
1.忽略线面平行、面面平行的判定定理使用的前提条件;
2.忽略定理的必备条件致误.
1.直线与平面平行的判定
应用判定定理证明线面平行的步骤:
上面的第一步“找”是证题的关键,其常用方法有:利用三角形、梯形中位线的性质;利用平行四边形的性质;利用平行线分线段成比例定理.
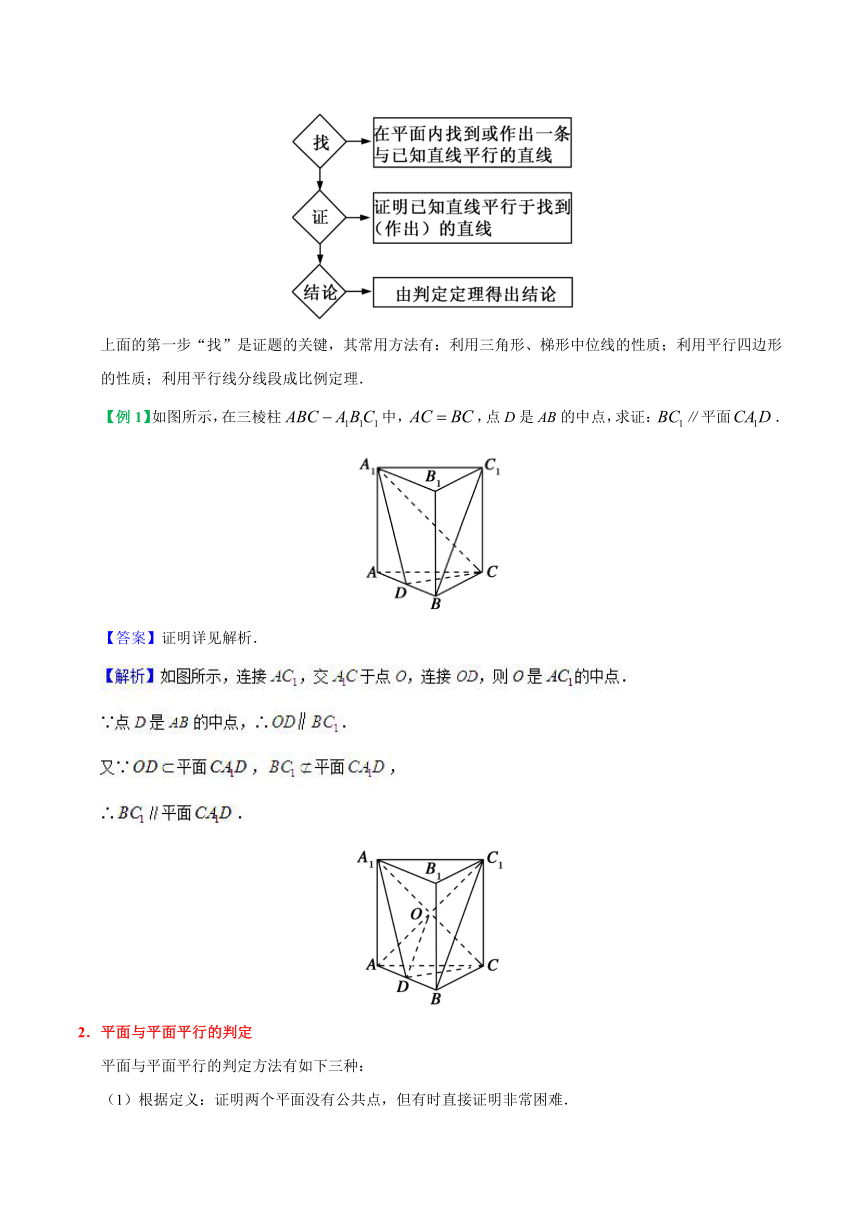
【例1】如图所示,在三棱柱中,,点D是AB的中点,求证:∥平面.
【答案】证明详见解析.
2.平面与平面平行的判定
平面与平面平行的判定方法有如下三种:
(1)根据定义:证明两个平面没有公共点,但有时直接证明非常困难.
(2)根据判定定理:要证明两个平面平行,只需在其中一个平面内找两条相交直线,分别证明它们平行于另一个平面,于是这两个平面平行,或在一个平面内找到两条相交的直线分别与另一个平面内两条相交的直线平行.
(3)根据平面平行的传递性:若两个平面都平行于第三个平面,则这两个平面互相平行.
【例2】如图,在长方体中,分别是的中点.求证:平面∥平面.
【答案】证明详见解析.
【名师点睛】利用判定定理证明两个平面平行的一般步骤:
第一步:在一个平面内找出两条相交直线;
第二步:证明这两条相交直线分别平行于另一个平面;
第三步:利用平面与平面平行的判定定理得出结论.
3.线面平行、面面平行的综合应用
在立体几何中,常见的平行关系有线线平行、线面平行和面面平行,这三种平行关系不是孤立的,而是相互联系,并且可以相互转化的. 在解决问题的过程中,要灵活运用平行关系的判定定理.
【例3】在正方体中,分别为的中点,N为BC的中点,试在四点中找两点,使这两个点与点N确定一个平面α且平面α∥平面.
【答案】三点确定的平面与平面平行.
【名师点睛】由平面与平面平行的判定定理知,只需所找的两点与点N构成的直线中,有两条相交直线与平面平行即可.
4.直线与平面平行的性质定理的应用
应用线面平行的性质定理时,关键是过已知直线作辅助平面与已知平面相交,所得交线与已知直线平行.还可以利用交线判断已知平面内任意一条直线与已知直线的位置关系,即在已知平面内所有与交线平行的直线都与已知直线平行,所有与交线相交的直线都与已知直线异面.
【例4】如图,在三棱柱中,点E,F分别是棱CC1,BB1上的点,点M是线段AC上的动点,EC=2FB=2,若平面AEF,试判断点M的位置.
【答案】M是AC的中点时,MB∥平面AEF.
5.平面与平面平行的性质定理的应用
利用面面平行的性质定理判断两直线平行的步骤:
(1)先找两个平面,使这两个平面分别经过这两条直线中的一条;
(2)判定这两个平面平行;
(3)再找一个平面,使这两条直线都在这个平面上;
(4)由定理得出结论.
【例5】已知三个平面α、β、γ满足α∥β∥γ,直线a与这三个平面依次交于点A、B、C,直线b与这三个平面依次交于点E、F、G.求证:.
【答案】证明详见解析.
【名师点睛】①当a与b共面时,有AE∥BF∥CG.上述证明过程也是正确的,只是此时B、H、F三点共线.
②连接,可同理证明.
③当a与b异面时,可过A(或B、C)作b的平行线或过E(或F、G)作a的平行线,再利用面面平行的性质定理可证得结论.
以上思路都遵循同一个原则,即“化异为共”.
6.直线、平面平行的综合应用
在立体几何中,线线平行、线面平行、面面平行之间可以相互转化.一般地,证明线面平行可以转化为证明线线平行;证明面面平行可以转化为证明线面平行;证明线线平行可以利用线面平行或面面平行的性质定理来实现.
【例6】如图,AB是圆O的直径,点C是圆O上异于A,B的点,直线PC⊥平面ABC,E,F分别是PA,PC的中点.记平面BEF与平面ABC的交线为l,试判断直线l与平面PAC的位置关系,并加以证明.
【答案】l∥平面PAC.证明详见解析.
7.忽略定理使用的前提条件致错
【例7】如果两条平行直线a,b中的a∥α,那么b∥α.这个命题正确吗?为什么?
【错解】这个命题正确.
∵a∥α,∴在平面α内一定存在一条直线c,使a∥c.
又∵a∥b,∴b∥c,∴b∥α.
【错因分析】忽略了b?α这种情况,从而导致错误,本题条件中的直线b与平面α有两种位置关系:b∥α和b?α.
【正解】这个命题不正确.
若b?α,∵a∥α,
∴在平面α内必存在一条直线c,使a∥c.
又∵a∥b,∴b∥c,∴b∥α.
若b?α,则不满足题意.
综上所述,b与α的位置关系是b∥α或b?α.
【易错警示】错误的原因是利用线面平行的判定定理时,忽略了定理使用的前提条件必须是平面外的一条直线与平面内的一条直线平行.
8.对平面与平面平行的性质定理理解不正确,忽略“第三个平面”这一条件
【例8】如图,α∥β,AB,CD是夹在平面α和平面β间的两条线段,则AC所在的直线与BD所在的直线平行,这个说法正确吗?
【错解】这个说法正确.
【错因分析】忽略了AB,CD可能异面的情况.当AB,CD异面时,AC与BD不平行.
【思路分析】AB,CD共面时,AC∥BD;AB,CD异面时,AC∥β,但AC与BD不平行.同理BD∥α,但BD与AC不平行.
【正解】这个说法错误.
【易错警示】使用定理证明或判断线线平行和线面平行时,一定要注意定理成立的条件,缺一不可.
基础训练
1.A,b,c为三条不重合的直线,α,β,γ为三个不重合平面,现给出六个命题
①?a∥b,②?a∥b,③?α∥β,
④?α∥β,⑤?α∥a,⑥?α∥a,
其中正确的命题是
A.①②③ B.①④⑤ C.①④ D.①③④
2.在正方体ABCD–A1B1C1D1中,与平面ACC1A1平行的棱共有
A.2条 B.3条 C.4条 D.6条
3.已知直线a,b,平面α,满足a?α,则使b∥α的条件为
A.b∥a B.b∥a且b?α
C.a与b异面 D.a与b不相交
4.如图,四棱锥P–ABCD中,M,N分别为AC,PC上的点,且MN∥平面PAD,则
A.MN∥PD B.MN∥PA
C.MN∥AD D.以上均有可能
5.直线m与平面α平行的充要条件是
A.直线m与平面α没有公共点
B.直线m与平面α内的一条直线平行
C.直线m与平面α内的无数条直线平行
D.直线m与平面α内的任意一条直线平行
6.平面α与平面β平行的条件可以是
A.α内有无穷多条直线与β平行
B.α内的任何直线都与β平行
C.直线a在平面α内,直线b在平面β内,且a∥β,b∥α
D.直线a∥α,直线a∥β
7.下列条件中,能得到两个平面平行的条件是
A.有一条直线与这两个平面都平行
B.有两条直线与这两个平面都平行
C.有一条直线与这两个平面都垂直
D.有一条直线与这两个平面所成的角相等
8.如图所示,三棱柱ABC–A1B1C1,D是BC的中点,D1是B1C1的中点.求证:
(1)A1B∥平面AC1D;
(2)平面A1BD1∥平面AC1D.
9.如图,在四棱锥P–ABCD中,PD⊥平面ABCD,底面ABCD为菱形,.点分E,F,G,H别是棱AB,CD,PC,PB上共面的四点,且BC∥EF.
证明:GH∥EF.
能力提升
10.下列四个命题中,不正确的是
A.若平面内有两条相交直线与平面内的两条相交直线分别平行,则两个平面平行
B.平行于同一平面的两个平面平行
C.如果平面内有无数条直线都与平面平行,则两个平面平行
D.如果平面内任意一条直线都与平面平行,则两个平面平行
11.过三棱柱ABC–A1B1C1的任意两条棱的中点作直线,其中与平面ABB1A1平行的直线共有
A.4条 B.6条 C.8条 D.12条
12.如图,下列四个正方体图形中,A、B为正方体的两个顶点,M、N、P分别为其所在棱的中点,能得出AB∥平面MNP的图形序号是
A.①② B.③④ C.②③ D.①④
13.如图,在四棱锥E–ABCD中,AB∥CD,且AB=2CD,F为BE的中点.
证明:FC∥平面ADE.
14.三棱柱ABC–A1B1C1中,若D为BB1上一点,M为AB的中点,N为BC的中点.求证:MN∥平面A1C1D.
15.如图,在空间四面体ABCD中,若E,F,G,H分别是AB,BD,CD,AC的中点,
(1)求证:四边形EFGH是平行四边形.
(2)求证:BC∥平面EFGH.
16.如图,已知正方体ABCD–A1B1C1D1中,M是AA1的中点,N是BB1的中点.
求证:平面MDB1∥平面ANC.
17.如图,已知四棱锥P–ABCD中,底面ABCD为平行四边形,点M,N,Q分别是PA,BD,PD的中点上,
(1)求证:MN∥PC;
(2)求证:平面MNQ∥平面PBC.
真题练习
18.(2019?四川模拟)如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q为所在棱的中点,则在这四个正方体中,直线AB与平面MNQ不平行的是
A. B.
C. D.
19.(2018?江苏节选)在平行六面体中,.
求证:;.
20.(2019?浙江模拟)如图,已知四棱锥P–ABCD,是以AD为斜边的等腰直角三角形,,CD⊥AD,PC=AD=2DC=2CB,E为PD的中点.证明:平面PAB.
21.(2018?新课标全国Ⅱ节选)如图,四棱锥P-ABCD中,侧面PAD为等边三角形且垂直于底面ABCD, E是PD的中点.证明:直线平面PAB.
22.(2019?北京模拟)如图,在四棱锥P?ABCD中,底面ABCD为正方形,平面PAD⊥平面ABCD,点M在线段PB上,PD//平面MAC,PA=PD=,AB=4.求证:M为PB的中点.
参考答案
1
2
3
4
5
6
7
10
11
12
18
C
A
B
B
A
B
C
C
B
D
A
1.【答案】C
2.【答案】A
【解析】如图所示,正方体ABCD–A1B1C1D1中,与平面ACC1A1平行的棱是BB1和DD1,共有2条.故选A.
3.【答案】B
【解析】∵a?α,∴b∥a?b∥α,或b?α,故A不成立;b∥a且b?α?b∥α,故B成立;a与b异面∴b∥α或b与α相交,故C不成立;a与b不相交?b∥α或b?α或b与α相交,故D不成立.故选B.
4.【答案】B
【解析】四棱锥P–ABCD中,M,N分别为AC,PC上的点,且MN∥平面PAD,MN?平面PAC,平面PAC∩平面PAD=PA,由直线与平面平行的性质定理可得:MN∥PA.故选B.
5.【答案】A
【解析】根据直线与平面平行的定义:直线与平面没有公共点时,直线与平面平行,所以“直线α与平面M没有公共点”是“直线α与平面M平行”的充要条件,故选A.
6.【答案】B
7.【答案】C
【解析】根据垂直于同一直线的两个平面互相平行,可得C正确.故选C.
8.【答案】证明详见解析.
【解析】(1)由题意,ABC–A1B1C1是三棱柱,
连接A1C,与AC1交于O,连接DO,可得A1B∥DO,
∵DO?平面AC1D,A1B?平面AC1D,∴A1B∥平面AC1D.
(2)由(1)可知A1B∥DO,D是BC的中点,D1是B1C1的中点.
∴D1B∥C1D,
∵DO、C1D?平面AC1D,DO∩C1D=D,
D1B、A1B?平面A1BD1,D1B∩A1B=B,
∴平面A1BD1∥平面AC1D.
9.【答案】证明详见解析.
【解析】∵BC∥EF,BC?平面EFGH,EF?平面EFGH,
∴BC∥平面EFGH,
∵BC?平面PBC,平面PBC∩平面EFGH=GH,
∴GH∥BC,
∵BC∥EF,∴GH∥EF.
10.【答案】C
11.【答案】B
【解析】作出如图的图形,H,G,F,I是相应直线的中点,故符合条件的直线只能出现在平面HGFI中,由此四点可以组成6条直线,故选B.
12.【答案】D
【解析】对于①,该正方体的对角面ADBC∥平面MNP,得出直线AB∥平面MNP;对于②,直线AB和平面MNP不平行,因此直线AB与平面MNP相交;对于③,易知平面PMN与正方体的侧面AB相交,得出AB与平面MNP相交;对于④,直线AB与平面MNP内的一条直线NP平行,且直线AB?平面MNP,∴直线AB∥平面MNP;综上,能得出直线AB∥平面MNP的图形的序号是①④.故选D.
13.【答案】证明详见解析.
14.【答案】证明详见解析.
【解析】三棱柱ABC–A1B1C1中,M为AB的中点,N为BC的中点,
∴MN∥AC,
又AC∥A1C1,
∴MN∥A1C1,
又MN?面A1C1D,A1C1?面A1C1D,
∴MN∥面A1C1D.
15.【答案】证明详见解析.
【解析】(1)∵在空间四面体ABCD中,
E,F,G,H分别是AB,BD,CD,AC的中点,
∴EF,EF=,GH,GH=,
∴EFGH,EF=GH,
∴四边形EFGH是平行四边形.
(2)∵E,H分别是AB、AC的中点,
∴EH∥BC,
∵EH?平面EFGH,BC?平面EFGH,
∴BC∥平面EFGH.
16.【答案】证明详见解析.
17.【答案】证明详见解析.
【解析】(1)由题意:P–ABCD是四棱锥,底面ABCD为平行四边形,
点M,N,Q分别是PA,BD,PD的中点上,连接AC,
∴N是AC的中点.
∴MN是三角形ACP的中位线,
∴MN∥PC.
(2)由(1)可得MN∥PC.
∵M,Q分别在PA,PD的中点上,
∴MQ是三角形ADP的中位线,
∴MQ∥PB.
由MQ∥PB,MN∥PC,PB?平面PBC,PC?平面PBC,PB∩PC=P,
同理MQ?平面MNQ,MN?平面MNQ,MQ∩MN=M.
∴平面MNQ∥平面PB C.
18.【答案】A
【名师点睛】本题主要考查线面平行的判定定理以及空间想象能力,属容易题.证明线面平行的常用方法:利用线面平行的判定定理,使用这个定理的关键是设法在平面内找到一条与已知直线平行的直线,可利用几何体的特征,合理利用中位线定理或者构造平行四边形、寻找比例式证明两直线平行.
19.【答案】证明详见解析.
【解析】在平行六面体ABCD-A1B1C1D1中,AB∥A1B1.
因为AB平面A1B1C,A1B1平面A1B1C,
所以AB∥平面A1B1C.
20.【答案】证明详见解析.
【解析】如图,设PA的中点为F,连接EF,FB.
因为E,F分别为PD,PA中点,所以且,
又因为,,所以且,
即四边形BCEF为平行四边形,所以,
因此平面PAB.
21.【答案】证明详见解析.
22.【答案】证明详见解析.
【解析】设交点为,连接.
因为平面,平面平面,所以.
因为是正方形,所以为的中点,所以为的中点.
