人教版高中数学必修二知识讲解,巩固练习(教学资料,补习资料):专题3.1 直线的倾斜角与斜率
文档属性
| 名称 | 人教版高中数学必修二知识讲解,巩固练习(教学资料,补习资料):专题3.1 直线的倾斜角与斜率 |

|
|
| 格式 | zip | ||
| 文件大小 | 784.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-21 00:00:00 | ||
图片预览




文档简介
知识
一、直线的倾斜角
1.直线的确定
在平面直角坐标系中,确定一条直线位置的几何要素是:已知直线上的一点和这条直线的方向,二者缺一不可.
2.直线倾斜角的概念
当直线l与x轴相交时,我们取x轴作为基准,x轴正向与直线l 方向之间所成的角α叫做直线l的倾斜角.
倾斜角与倾斜程度
平面直角坐标系内每一条直线都有一个确定的倾斜角,且倾斜程度相同的直线,其倾斜角相等;倾斜程度不同的直线,其倾斜角不相等.因此,我们可用倾斜角表示平面直角坐标系内一条直线的倾斜程度.
3.倾斜角的取值范围
当直线l与x轴平行或重合时,我们规定它的倾斜角为0°.因此,直线的倾斜角α的取值范围是 .
如下图:的倾斜角为0°,的倾斜角为锐角,的倾斜角为直角,的倾斜角为钝角.
二、直线的斜率
1.斜率的定义
我们把一条直线的倾斜角α的 叫做这条直线的斜率,通常用小写字母k表示,即.
注:倾斜角是90°的直线没有斜率.
2.斜率与倾斜角之间的关系
当直线的倾斜角α=0°时,斜率k=0,直线与x轴 ;?
当0°<α<90°时,斜率k>0,且k值增大,倾斜角随着 ;?
当α=90°时,斜率k (此时直线是存在的,直线与x轴垂直);?
当90°<α<180°时,斜率k<0,且k值增大,倾斜角也随着 .?
3.直线的倾斜程度
(1)倾斜角α不是90°的直线都有斜率,倾斜角不同,直线的斜率也不同.因此,我们可以用 表示直线的倾斜程度.
(2)直线的斜率和倾斜角都是刻画直线倾斜程度的量,斜率侧重于代数角度,倾斜角侧重于几何角度.
三、过两点的直线的斜率公式
1.公式
经过两点的直线的斜率公式为 .
2.公式的推导
如图(1),(2),设直线的倾斜角为α(α≠90°),当直线的方向(即从指向的方向)向上时,过点作x轴的平行线,过点作y轴的平行线,两条直线相交于点Q,于是点Q的坐标为.
如图(1),当α为锐角时,.
在中,.?
如图(2),当α为钝角时,α=180°?θ(设),..
在中,,
于是可得,即.?
同样,当直线的方向向上时,如图(3),(4),也有,即.?
综上所述,经过两点的直线的斜率公式为 .
名师提醒
(1)当直线的倾斜角为时,斜率公式不适用,因此在研究直线的斜率问题时,一定要注意斜率的存在与不存在两种情况.
(2)斜率计算公式中的值与所选取的两点在直线上的位置无关,两纵坐标和两横坐标在公式中的次序可以同时调换.
(3)当直线与轴平行或重合时,直线的斜率公式成立,此时.
四、两直线平行
1.特殊情况下的两条直线平行的判定
两条直线中有一条直线没有斜率,当另一条直线的斜率也不存在时,两直线的倾斜角都为 ,故它们互相平行.
2.两条直线的斜率都存在时,两条直线平行的判定
两条直线都有斜率而且不重合时,如果它们平行,那么它们的 相等;反之,如果它们的斜率相等,那么它们 ,即.
证明如下:
设两条直线的斜率分别为.
如果(如图),那么它们的倾斜角相等,即.∴,∴.
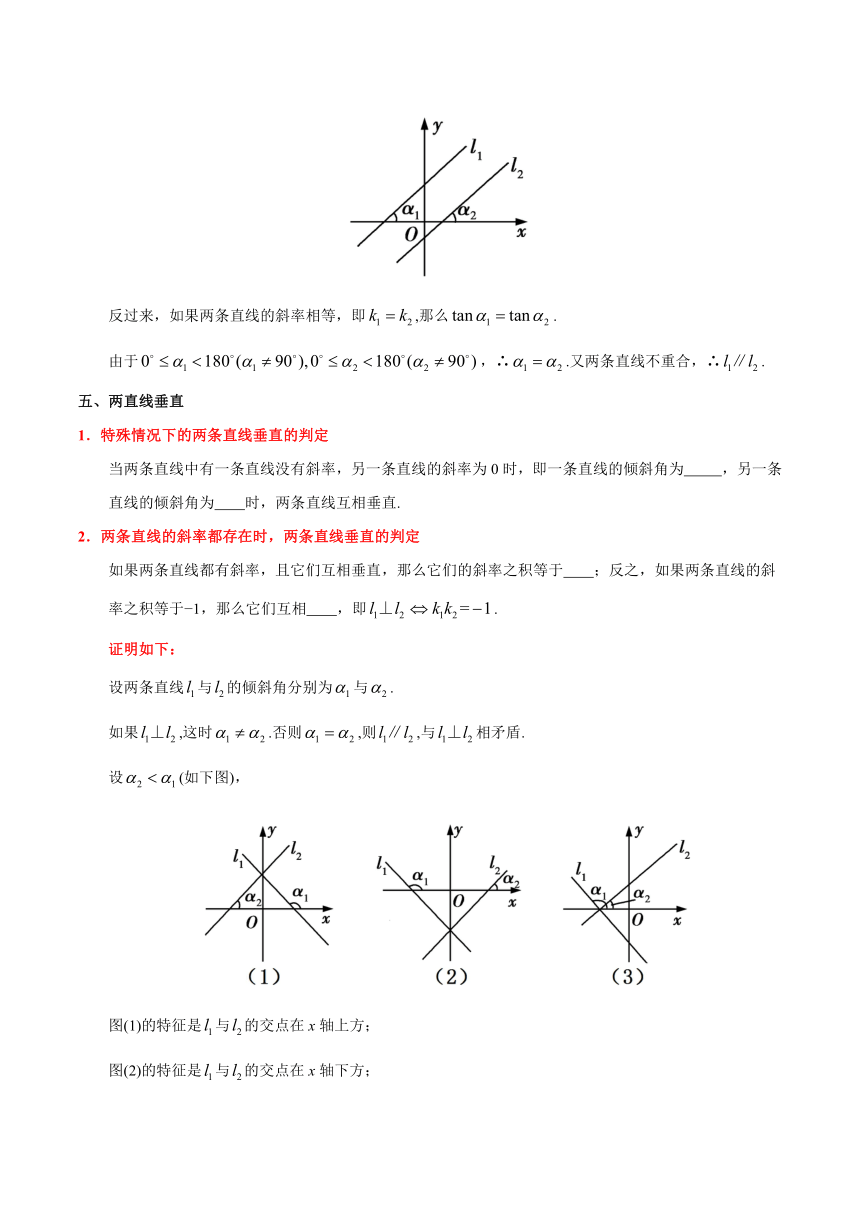
反过来,如果两条直线的斜率相等,即,那么.
由于,∴.又两条直线不重合,∴.?
五、两直线垂直
1.特殊情况下的两条直线垂直的判定
当两条直线中有一条直线没有斜率,另一条直线的斜率为0时,即一条直线的倾斜角为 ,另一条直线的倾斜角为 时,两条直线互相垂直.
2.两条直线的斜率都存在时,两条直线垂直的判定
如果两条直线都有斜率,且它们互相垂直,那么它们的斜率之积等于 ;反之,如果两条直线的斜率之积等于?1,那么它们互相 ,即.
证明如下:
设两条直线与的倾斜角分别为与.?
如果,这时.否则,则,与相矛盾.?
设(如下图),?
图(1)的特征是与的交点在x轴上方;?
图(2)的特征是与的交点在x轴下方;?
图(3)的特征是与的交点在x轴上,无论哪种情况下都有.?
∵,的斜率分别是,且,∴.?
∴.∴,即.?
反过来,若,即.不失一般性,设,则,即,
∴.
知识参考答案:
一、2.向上
3.0°≤α<180°
二、1.正切值
2.平行或重合 增大 不存在 增大
3.斜率
四、1.90°
2.斜率 平行
五、1.90° 0°
2.?1 垂直
重点
重点
直线的斜率、过两点的直线的斜率公式、两条直线的平行、垂直关系
难点
直线的倾斜角与斜率的关系、两条直线平行与垂直的综合应用
易错
直线的倾斜角与斜率的变化关系、斜率不存在的情况
1.求直线的斜率
(1)已知倾斜角求斜率时,若,根据公式直接计算.当倾斜角未给出时,可根据直线与其他直线的位置关系(如平行、垂直等)确定出所求直线的倾斜角,再代入计算.
(2)已知两点求直线的斜率时,首先应检验两点的横坐标是否相等.若相等,则斜率不存在;若不相等,则可用斜率公式直接计算.
【例1】经过两点A(4,2y+1),B(2,-3)的直线的倾斜角为45°,则y?的值为
A.-1 B.-3
C.0 D.2
【答案】A
【例2】已知点M,N的坐标分别是,直线l经过点,且与线段MN相交.?
(1)求直线PM与PN的斜率;
(2)求直线l的斜率k的取值范围.
【解析】(1)由题意与斜率公式可知,直线PM与PN的斜率分别为.?
(2)如图,直线l相当于绕着点P在直线PM与PN间旋转,l′是过P点且与x轴垂直的直线,当l由PN位置旋转到l′位置时,倾斜角增大到90°,又,∴.?
当l从l′位置旋转到PM位置时,倾斜角大于90°,又,∴.?
综上所述,.
【归纳总结】求直线的斜率的方法:
(1)定义法.已知直线的倾斜角为α,且α≠90°,则斜率.
(2)公式法.若直线过两点,且,则斜率.
(3)数形结合法.已知一条线段AB的端点及线段外一点P,求过点P的直线l与线段AB有交点的情况下l的斜率,若直线PA,PB的斜率均存在,则步骤为:
①连接PA,PB;
②由求出;
③结合图形即可写出满足条件的直线l的斜率的取值范围.
2.三点共线问题
两点即可确定一条直线,要证三点共线,只要证过同一点的两直线的斜率相等即可.用斜率公式解决三点共线问题时,首先要估测三点中是否任意两点的连线垂直于x轴,即斜率不存在的情况.斜率存在的前提下,当三点中任意两点所确定的直线的斜率相等时,三点共线.
【例3】求证:三点共线.
【名师点评】若点A、B、C都在某条斜率存在的直线上,那么由任意两点的坐标都可以确定这条直线的斜率,即;若或,则直线AB与BC或AB与AC的斜率相同,且又过同一点B或A,因此直线AB与BC或AB与AC重合.
【例4】若A(-1,-2),B(4,8),C(5,x),且A,B,C三点共线,求x的值.
【解析】由题意,可知直线AB,AC的斜率存在,
又A,B,C三点共线,则kAB=kAC,即,解得x=10.
3.直线的斜率、倾斜角的应用
解决几何图形中直线的倾斜角与斜率的综合问题时,要善于利用几何图形的几何性质,注意倾斜角是几何图形中的夹角还是它的邻补角;也可以利用经过两点的直线的斜率公式,先求斜率,再求倾斜角.
光的反射问题中,反射角等于入射角,但反射光线所在直线的斜率并不等于入射光线所在直线的斜率.当镜面水平放置时,上述斜率之间是互为相反数的关系.另外,在光的反射问题中也经常使用对称的方法求解.
【例5】光线从点A(2,1)射到y轴上的点Q,经y轴反射后过点B(4,3),试求点Q的坐标及入射光线的斜率.
4.直线的倾斜角与斜率的关系
(1)直线的倾斜角α与斜率k的关系:,由直线的倾斜角能求斜率,反过来,由直线的斜率能求倾斜角.注意倾斜角的取值范围是.
(2)在范围内,,且k随着α的增大而增大;在范围内,,且k随着α的增大而增大.但在范围内, k并不是随着α的增大而增大的.
【例6】已知直线l的倾斜角范围为[45°,135°],求直线l的斜率的范围.?
【解析】应进行分类讨论:
当倾斜角α=90°时,l的斜率不存在;?
当α[45°,90°)时,l的斜率;?
当α(90°,135°]时,l的斜率.?
∴l的斜率不存在或斜率.
5.两条直线的平行关系
在判断两条直线是否平行时,首先应判断直线的斜率是否存在,然后根据斜率的关系进行判断,同时不要漏掉两条直线重合的情况.
【例7】根据下列给定的条件,判断直线l1与直线l2是否平行.
(1)l1经过点Α(2,1),B(-3,5),l2经过点C(3,-3),D(8,-7);
(2)l1经过点E(0,1),F(-2,-1),l2经过点G(3,4),H(2,3);
(3)l1的倾斜角为60°,l2经过点,;
(4)l1平行于y轴,l2经过点P(0,-2),Q(0,5).
6.两条直线的垂直关系
判断两条直线是否垂直的依据是:在这两条直线都有斜率的前提下,只需看它们的斜率之积是否等于?1即可,但应注意有一条直线与x轴垂直,另一条直线与x轴平行或重合时,这两条直线也垂直.
【例8】根据下列给定的条件,分别判断直线l1与l2是否垂直:
(1)l1经过点A(1,3),B(-1,-1),l2经过点C(2,1),D(4,0);
(2)l1经过点E(-1,3),F(-1,-5),l2经过点G(2,4),H(-1,4);
(3)l1的倾斜角为30°,l2经过点M(1,),N(2,0);
(4)l1经过点P(2,-1),Q(3,4),l2经过点R(5,2),S(0,1).
【思路点拨】若斜率均存在,求出斜率,利用进行判断,注意数形结合及斜率不存在的特殊情况.
7.根据直线的位置关系求参数
已知两直线平行或垂直求解参数的相关问题时,首先需考虑直线的斜率是否存在,若斜率都存在,则依据斜率间的关系求解;若斜率不存在,则需注意特殊情形.此外,已知两直线垂直求解参数时,还需注意斜率是否为零.
【例9】已知直线经过点,直线经过点.
(1)若,求的值;
(2)若,求的值.
【解析】由题意知直线的斜率存在且.
(1)若,则直线的斜率也存在,又,
由,得,解得或.
经检验,当或时, .
(2)若,当时, ,,不符合题意;
当时,直线的斜率存在且不为0,则直线的斜率也存在,且,即,解得或.
经检验,当或时,.
【例10】已知点A(?2,?5),B(6,6),点P在y轴上,且∠APB=90°,则点P的坐标为
A.(0,?6) B.(0,7)
C.(0,?6)或(0,7) D.(?6,0)或(7,0)
【答案】C
8.两直线平行和垂直的综合应用
利用直线平行与垂直的条件判断三角形或四边形的形状是常见题型,同时要熟知各种图形的特点及判定方法.证明两直线平行时,仅有斜率相等是不够的,注意排除两直线重合的情况.
【例11】已知,试判断四边形ABCD的形状.
【解析】由题意,可得,
∴.
∴AB∥CD,BC∥DA.
∴四边形ABCD为平行四边形.
又,
∴直线AB与BC垂直,即∠ABC=90°.
∴四边形ABCD为矩形.
【思路点拨】画图直观猜想四边形ABCD是矩形.要说明四边形ABCD为矩形,只要计算,再结合两条直线平行、垂直的判定求解即可.
9.求直线的倾斜角时忽略斜率不存在的情况
【例12】求经过A(m,3),B(1,2)两点的直线的斜率,并指出倾斜角α的取值范围.
【错解】由斜率公式可得直线AB的斜率.
当m>1时,,所以直线的倾斜角α的取值范围是0°<α<90°;
当m<1时,,所以直线的倾斜角α的取值范围是90°<α<180°.
【错因分析】利用斜率公式求直线的斜率的条件是“”.而错解中没有考虑m=1的情况,忽略了斜率不存在的情况.
【正解】当m=1时,直线AB的斜率不存在,此时直线的倾斜角α=90°.?
当m≠1时,由斜率公式可得直线AB的斜率,?
当m>1时,,所以直线的倾斜角α的取值范围是0°<α<90°;?
当m<1时,,所以直线的倾斜角α的取值范围是90°<α<180°.
【误区警示】求直线斜率时,一定要根据题目条件对斜率是否存在作出判断,以免漏解.
10.忽略直线斜率的存在性致错
【例13】已知,若直线,求的值.
【错解】由斜率公式知,,.
∵,∴,即,解得m=1,
∴m的值为1.
【错因分析】漏掉了直线斜率不存在的情况.
【正解】∵A,B两点纵坐标不相等,∴AB与x轴不平行.
∵AB⊥CD,∴CD与x轴不垂直,.
当AB与x轴垂直时,,解得,而时,C,D纵坐标均为,则CD∥x轴,此时AB⊥CD,满足题意.
当AB与x轴不垂直时,由斜率公式知,,
.
∵AB⊥CD,∴,即,解得m=1.
综上,m的值为1或.
【误区警示】对于含有参数的直线垂直问题,要分斜率存在和斜率不存在两种情况讨论,避免漏解.
基础训练
1.关于直线的倾斜角与斜率,下列说法正确的是
A.所有的直线都有倾斜角和斜率
B.所有的直线都有倾斜角,但不一定都有斜率
C.直线的倾斜角和斜率有时都不存在
D.所有的直线都有斜率,但不一定有倾斜角
2.已知直线经过点与点,则该直线的倾斜角为
A.150° B.75°
C.135° D.45°
3.直线的斜率为2,,直线l2过点,且与y轴交于点P,则P点坐标为
A. B.
C. D.
4.如图,设直线l1,l2,l3的斜率分别为k1,k2,k3,则k1,k2,k3的大小关系为
A. B.
C. D.
5.若直线l经过点(a?2,?1)和(?a?2,1),且与斜率为的直线垂直,则实数a的值是
A. B.
C. D.
6.已知A(?4,2),B(6,?4),C(12,6),D(2,12),则下面四个结论:①AB∥CD;②AB⊥AD;③AC∥BD;④AC⊥BD中正确的个数为
A.1 B.2
C.3 D.4
7.若l1过点A(m,1),B(?3,4),l2过点C(0,2),D(1,1),且,则m=__________.
8.若过点P(1,1),Q(3,2a)的直线的倾斜角为钝角,则实数a的取值范围是__________.?
9.求经过下列两点的直线的斜率,并判断其倾斜角是锐角、直角还是钝角.
(1)A(0,-1),B(2,0).
(2)P(5,-4),Q(2,3).
(3)M(3,-4),N(3,-2).
10.当m为何值时,过A(1,1),B(2m2+1,m?2) 两点的直线:
(1)倾斜角为135°;
(2)与过两点(3,2),(0,?7)的直线垂直;
(3)与过两点(2,?3),(?4,9)的直线平行?
11.已知A(1,5),B(?1,1),C(3,2),若四边形ABCD是平行四边形,求D点的坐标.
能力提升
12.已知M(a,b),N(a,c)(b≠c),则直线MN的倾斜角是
A.不存在 B.45°
C.135° D.90°
13.如果直线l过点(1,2),且不通过第四象限,那么l的斜率的取值范围是
A.[0,1] B.[0,2]
C. D.(0,3]
14.若直线的斜率是方程的两根,则l1与l2的位置关系是
A.平行 B.重合
C.相交但不垂直 D.垂直
15.已知经过点A(3,n),B(5,m)的直线l1与经过点P(-m,0),Q(0,n2)(mn≠0)的直线l2平行,则的值为
A.-1 B.-2
C.-1或2 D.-2或1
16.设点A(2, -3) ,B(-3, -2),直线l过点P(1, 1)且与线段AB相交,则l的斜率k的取值范围是
A.或k≤- 4 B.-4≤k<
C.≤k≤4 D.以上都不对
17.如图,菱形ABCD中,∠BAD=60°,求菱形各边和两条对角线所在直线的倾斜角与斜率.
18.在平面直角坐标系中,四边形OPQR的顶点坐标按逆时针顺序依次为O(0,0)、P(1,t)、Q(1-2t,2+t)、R(-2t,2),其中t>0.试判断四边形OPQR的形状.
参考答案
1
2
3
4
5
6
12
13
14
15
16
B
C
D
A
A
C
D
B
D
C
A
1.【答案】B
【解析】任何直线都有倾斜角,但是并不是所有的直线都有斜率,当直线的倾斜角为直角时,直线的斜率不存在,所以A,C,D错误,B正确,故选B.
2.【答案】C
【解析】直线的斜率为,又倾斜角,,所以,故选C.
3.【答案】D
4.【答案】A
【解析】根据“斜率越大,直线的倾斜程度越大”可知选项A正确.
5.【答案】A
【解析】直线l的斜率为,依题意得,∴.
6.【答案】C
【解析】由题意得
,所以AB∥CD,AB⊥AD,AC⊥BD.
7.【答案】0
【解析】∵l1∥l2,且,∴,∴m=0.
8.【答案】(-∞,)
【解析】本题考查直线的倾斜角和斜率的关系.因为kPQ=,又kPQ=tan α,90°<α<180°,则tan α<0,即<0,∴a<.
9.【解析】(1),
因为kAB>0,所以直线AB的倾斜角是锐角.
(2),
因为kPQ<0,所以直线PQ的倾斜角是钝角.
(3)因为xM=xN=3,
所以直线MN的斜率不存在,其倾斜角为直角.
11.【解析】设D(x,y),则,,,,
由AB∥CD,得,即y=2x?4.①
由AD∥BC,得,即x?4y+19=0.②
由①②解得.
∴D点的坐标为(5,6).
12.【答案】D
【解析】∵MN⊥x轴,∴直线MN的倾斜角为90°.
13.【答案】B
【解析】过点(1,2)的斜率为非负且最大斜率为此点与原点的连线的斜率时,图象不过第四象限,故l的斜率的取值范围是[0,2].
14.【答案】D
【解析】因为方程有两个不相等的实数根,直线l1,l2的斜率是方程的两根,所以,且,所以l1与l2垂直.故选D.
15.【答案】C
16.【答案】A
【解析】,画图如图所示,观察可知或.
17.【解析】由题意可得AD∥BC,从而可知AD与BC所在直线的倾斜角都为60°,其斜率都为tan 60°=.
又AB∥CD,且AB与x轴重合,
所以AB与CD所在直线的倾斜角都为0°,其斜率都为tan 0°=0.
因为AC和BD都是菱形的对角线,
所以AC与BD所在直线的倾斜角分别为αAC=30°,αBD=120°,其斜率分别为kAC=tan 30°=,kBD=
tan 120°=.
