人教A版高中数学必修一:2.2.2对数函数及其性质(1)教案
文档属性
| 名称 | 人教A版高中数学必修一:2.2.2对数函数及其性质(1)教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 106.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-22 20:59:19 | ||
图片预览

文档简介
课题
对数函数及其性质(1)
课型
新授课
教学
目标
理解对数函数的概念;
掌握对数函数的图象、性质;
重点
难点
教学重点:对数函数的图象、性质.
教学难点:对数函数的图象与指数函数的关系.
教具
准备
多媒体课件
课时
安排
1课时
教学过程与教学内容
教学方法、教学手段与学法、学情
一.复习引入
1、对数的概念:
如果ax=N,那么数x叫做以a为底N的对数,
记作logaN=x(a>0,a≠1)
指数函数的定义:
函数 y=ax (a>0,且a≠1) 叫做指数函数,其中x是自变量,函数的定义域是 R.
3、 我们研究指数函数时,曾经讨论过细胞分裂问题,某种细胞分裂时,得到的细胞的个数是分裂次数的函数,这个函数可以用指数函数=表示.
现在,我们来研究相反的问题,如果要求这种细胞经过多少次分裂,大约可以得到1万个,10万个……细胞,那么,分裂次数就是要得到的细胞个数的函数.根据对数的定义,这个函数可以写成对数的形式就是.
如果用表示自变量,表示函数,这个函数就是.
引出新课--对数函数.
二、新课讲解:
1.对数函数的定义:
函数叫做对数函数,定义域为,值域为.
例1. 求下列函数的定义域:
(1); (2); (3).
分析:此题主要利用对数函数的定义域(0,+∞)求解.
解:(1)由>0得,∴函数的定义域是;
(2)由得,∴函数的定义域是
(3)由9得-3,
∴函数的定义域是.
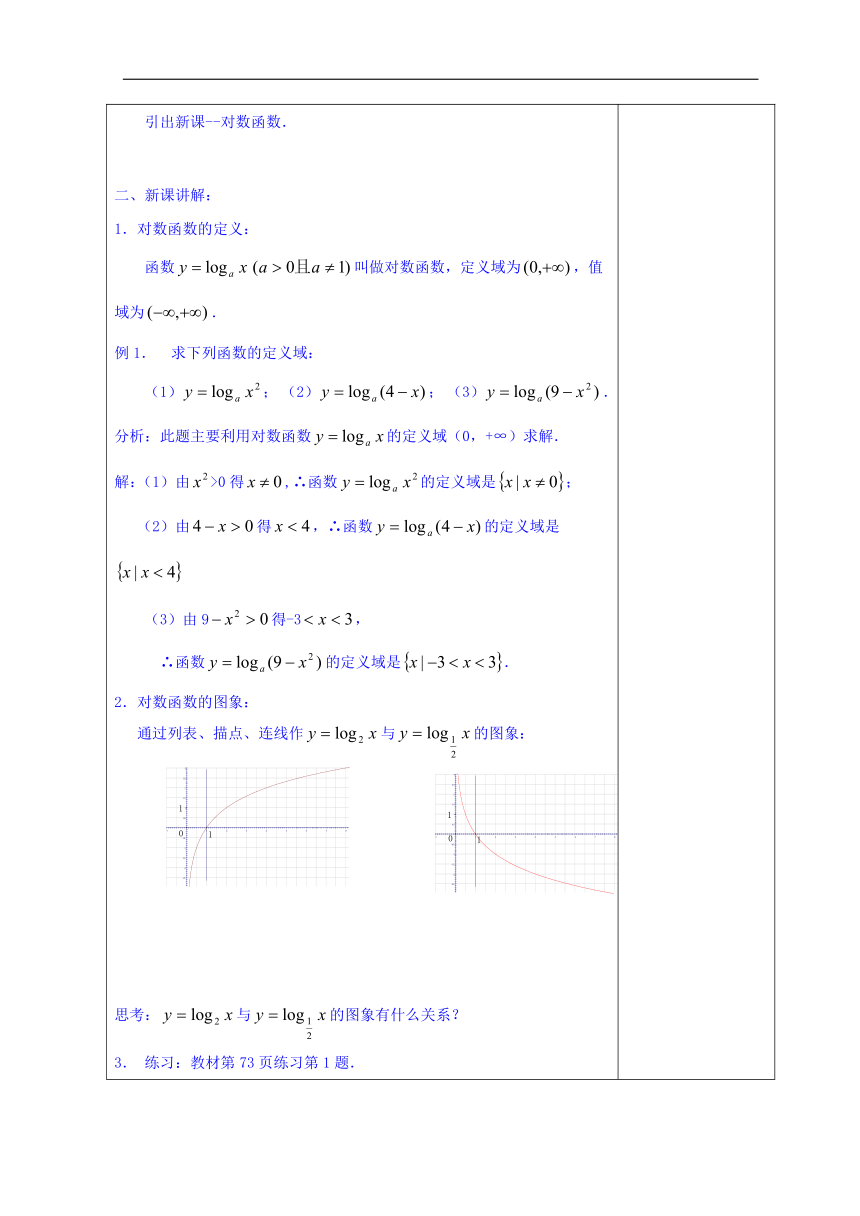
2.对数函数的图象:
通过列表、描点、连线作与的图象:
思考:与的图象有什么关系?
3. 练习:教材第73页练习第1题.
1.画出函数y=x及y=的图象,并且说明这两个函数的相同性质和不同性质.
解:相同性质:两图象都位于y轴右方,都经过点(1,0),
这说明两函数的定义域都是(0,+∞),且当x=1,y=0.
不同性质:y=x的图象是上升的曲线,y=的图象是下降的曲线,这说明前者在(0,+∞)上是增函数,后者在(0,+∞)上是减函数.
4.对数函数的性质
由对数函数的图象,观察得出对数函数的性质.
a>1
0<a<1
图
象
性
质
定义域:(0,+∞)
值域:R
过点(1,0),即当x=1时,y=0
时
时
时
时
在(0,+∞)上是增函数
在(0,+∞)上是减函数
三.课堂练习(P73、2)求下列函数的定义域:
(1)y=(1-x) (2)y= (3)y=
(5) (6)
解:(1)由1-x>0得x<1 ∴所求函数定义域为{x|x<1};
(2)由x≠0,得x≠1,又x>0 ∴所求函数定义域为{x|x>0且x≠1};
(3)由 ∴所求函数定义域为{x|x<};
(4)由 ∴x≥1 ∴所求函数定义域为{x|x≥1}.
四.课堂小结
⑴对数函数定义、图象、性质;
⑵对数的定义, 指数式与对数式互换;
⑶比较两个数的大小.
五.课后作业:
1.阅读教材第70~72页;?
板
书
对数函数及其性质(1)
1.对数函数的定义:
函数叫做对数函数,定义域为,值域为.
2.对数函数的图象及其性质
a>1
0<a<1
图
象
性
质
定义域:(0,+∞)
值域:R
过点(1,0),即当x=1时,y=0
时
时
时
时
在(0,+∞)上是增函数
在(0,+∞)上是减函数
教学
反思
